基于新型传感器阵列的声全息测试分析方法研究

陈允锋， 刘 超， 吕曜辉

(1.海军驻无锡地区军事代表室,江苏 无锡 214061； 2.海鹰企业集团有限责任公司,江苏 无锡 214000；3.中国科学院 声学研究所,北京 100190)



基于新型传感器阵列的声全息测试分析方法研究

陈允锋1， 刘 超2， 吕曜辉3

(1.海军驻无锡地区军事代表室,江苏 无锡 214061； 2.海鹰企业集团有限责任公司,江苏 无锡 214000；3.中国科学院 声学研究所,北京 100190)

针对声全息技术在实际工程应用中的扫描相位误差和有限测量孔径的问题，通过改进测试阵列和算法优化两种途径对其进行分析和解决。使用基于数字麦克风的面阵进行快照法测量，代替了传统的扫描测量，规避了扫描引入的相位误差；从理论上分析了有限孔径下近场声全息重构误差产生机理，并提出了“有限孔径空间扩展+波数域迭代滤波”的声全息算法，选用简谐激励作用下四周为无限大障板的简支钢板为对象，与传统声全息算法结果对比，验证了算法的有效性，并分析了全息面数据空间补零长度和迭代循环次数对声场重构的影响；使用转子台作为被测设备，模拟已知故障，通过单参考源下传感器阵列扫描测量结果验证了算法可以准确地定位模拟故障的空间位置。

近场声全息； 数字麦克风； 面阵； 有限测量孔径； 波数域滤波； 迭代

0 引 言

场声全息技术可以准确实现噪声源定位识别以及辐射声场可视化，对制定振动噪声控制方案具有重要的参考价值。由于计算简单和准确高效，基于空间声场变换的近场声全息算法在工程上得到了大量的应用，但为了降低声场重构误差，其要求全息测量孔径至少为声源尺寸4倍以上[1]，对于舰艇、飞机等大尺寸结构声源，满足这一条件显然不太现实。

现有平面声全息测试系统一般采用线阵扫描的方式。扫描时，固定一个参考通道，全息面上测点的复声压中相位由各测点声压与参考通道的相位差确定。线阵扫描测量虽然能够降低系统复杂度，节省成本，但会引入相位误差，加剧通道不一致性产生的影响，且无法用于非稳态声场的测量。使用基于面阵的快照法测试可解决上述问题。然而，声全息算法对于阵列孔径的要求会使得面阵的规模巨大，系统复杂度和成本增加，不利于实际应用。因此，在有限的阵列规模下获得较为精确的声场重构结果成为了一个亟待解决的问题。针对这一问题，国内外已开展了很多研究，Williams E G等人[2,3]在全息面复声压数据外推过程中引入了改进型Tikhonov正则化处理，根据偏差理论实现了正则化因子在迭代过程中的自适应选择，并对该方法有效性进行了验证；毕传兴等人对基于空间声场变换的有限孔径近场声全息方法进行了理论研究，并提出了基于PGA[4]以及波叠加法[5]的Patch近场声全息方法。

在工程实际中，如何通过局部孔径测量获得覆盖整个大尺寸结构声源表面的声场分布是一个重要问题，目前鲜有研究。

针对上述问题，本文首先根据空间声场变换的近场声全息其理论分析了全息重构误差的成因及解决方法，继而提出了针对有限孔径声全息测量面的基于“有限孔径空间扩展+波数域迭代滤波”的全息变换方法，通过数值仿真对该方法进行了深入分析，并在试验中验证了方法的可行性。

1 基于空间变换的近场平面声全息

由均匀理想流体媒质中小振幅声波的波动方程，可以得到不依赖时间的单频声波场Helmholtz方程

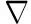
(1)

选择格林函数G(x,y,z)，使其满足Dirichlet边界条件，则格林函数GD(x,y,z)的形式为

(2)

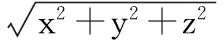
(3)

将式(3)两边进行二维傅里叶(Fourier)变换，并根据卷积定理可推导平面声全息公式

(4)

2 有限孔径平面全息误差及消除

基于空间变换的近场平面声全息在实际应用中误差主要来源如下：

1)在实际测量中，由于测试环境和硬件处理能力的限制，只能在有限全息测量孔径上获得被测复声压信号，由此,得到的数据对分布在无限大全息平面上的复声压信号进行了截断，忽略了全息测量孔径外声场信息的贡献，将导致重建结果的误差。

2)对定义在无穷平面上的格林函数也要进行截断，导致产生重建结果的误差。

3)根据信号处理理论，在利用傅立叶变换计算时，因有限孔径尺寸将可能产生泄漏误差。

4)使用二维傅里叶变换将全息面复声压由空间域转换到波数域，产生的高波数分量对测量时引入的噪声具有放大作用，导致重建结果的误差。

2.1 有限孔径空间扩展

在有限测量孔径条件下，若全息面不能完全覆盖被测声源，即全息面边缘部分仍然存在较高的能量，对全息面直接进行二维傅里叶变换时，由于截断，将在变换结果中引入高波数分量，高波数分量的存在将放大全息面噪声，从而无法得到正确的变换结果，因此在变换前，需对全息面在空间上进行扩展，使外推后的全息面声压平坦缓慢衰减。具体步骤如下：

1)设全息测量面为P0，大小为L×L，将P0如图1扩展为P，P的大小为L′×L′(L′>L)，扩展区域设为P′，声压置“0”。图1中内圈6行部分为全息面P0，外圈2行部分为P′。

2)对扩展的全息面P'进行二维傅里叶变换，从空间域变换到波数域，得到波数域的复声压。

3)选择合适的波数域滤波器滤除傅里叶变换结果中的高波数分量。

4)对波数域外推计算得到的结果进行二维傅里叶逆变换，得到新的扩展孔径下空间域全息面复声压，并将其位于局部孔径P0内的复声压数据用实际测量的复声压数据替换得到新的扩展全息面复声压数据。

5)将新的扩展全息面复声压数据作为输入，代入步骤(2)～步骤(4)进行迭代循环计算，减小扩展孔径内估计得到的复声压数据与实际复声压数据之间的误差。

经过以上步骤可将有限孔径下的测量结果扩展为适合全息变换的全息面复声压数据。采用迭代循环后计算得到的扩展孔径下空间域全息面复声压进行声场全息重构。提取将重构结果中对应实际全息测量面P0的结果，即完成了有限孔径下平面声全息分析。

2.2 波数域滤波

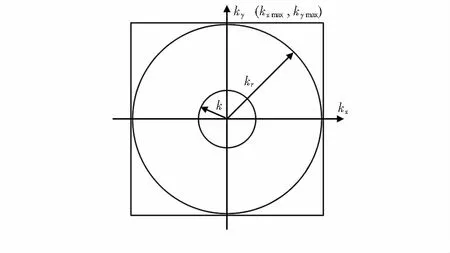
图2 波数域分布

在krk的区域，辐射声波为随距离呈指数衰减的倏逝波，由Green函数的表达式可知，当kr>k时，Green函数的值随kr的增大而减小，图3为当频率f=1 000Hz，测量距离zH-zs=0.1m时,Green函数的幅值随kr的变化，此时k=18.32。

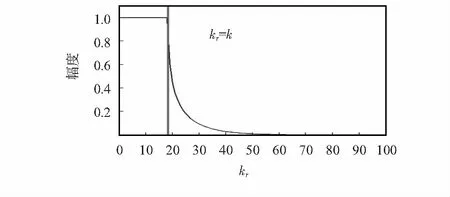
图3 Green函数幅度随kr的变化

由上所述，可对全息面声压二维傅里叶变换的结果在波数域进行滤波处理，滤除变换平面中高波数部分，以消除全息面噪声引入的误差。

3 数值仿真

3.1 有效性验证

选用简谐激励作用下四周为无限大障板的简支钢板为对象，开展基于“有限孔径空间扩展+波数域迭代滤波”的近场声全息方法声场重构仿真分析。简支板的长和宽均为0.5m，厚度为0.005m，杨氏模量为2.0×1011Pa，泊松比为0.28，密度为7.8×103kg/m3；激励力幅值为1N，作用点为(0.2，0.2)m，辐射声场的空间媒质为空气，取其声速为343m/s。在声场计算过程中，全息测量面距离简支板表面为0.05m，重建面为平板表面；全息面及重建面上复声压理论值根据瑞利积分[7]得到，其中全息面复声压在理论计算的基础上，添加高斯白噪声，信噪比为30dB；考虑到858Hz为简支板第(3，3)阶模态，故选其作为分析频率。

选定全息面大小尺寸为0.25m×0.25m，测量点数为16×16，此时全息测量面孔径仅为简支板表面的1/4。采用本文方法计算声场分布时，全息面补零至原始测量数据长度的2倍，迭代次数选择2 000。图4为声场重构效果对比，可以发现:在局部孔径测量下，若直接采用常规全息算法进行声场重构，声压幅值分布产生很大误差，并在重构面边缘出现比较严重“吉布斯”效应；而采用迭代滤波近场声全息方法，通过全息面数据外推计算，则能够准确实现声源面声场全息重构。

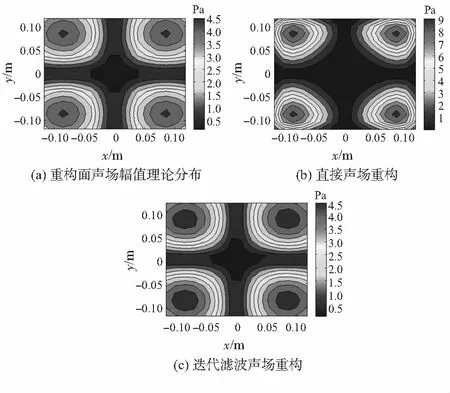
图4 声场重构效果对比

3.2 迭代次数与扩展区域对声场重构影响

在全息面补零至原始测量数据长度2倍的情况下，计算分析了不同迭代次数对声场重构的影响，具体如图5所示。可以发现：随着迭代次数的升高，声场重构结果与理论值的误差均逐渐变小，当迭代次数超过1 000后，误差趋于稳定；在实际工程中，建议迭代次数选用1 000以上。

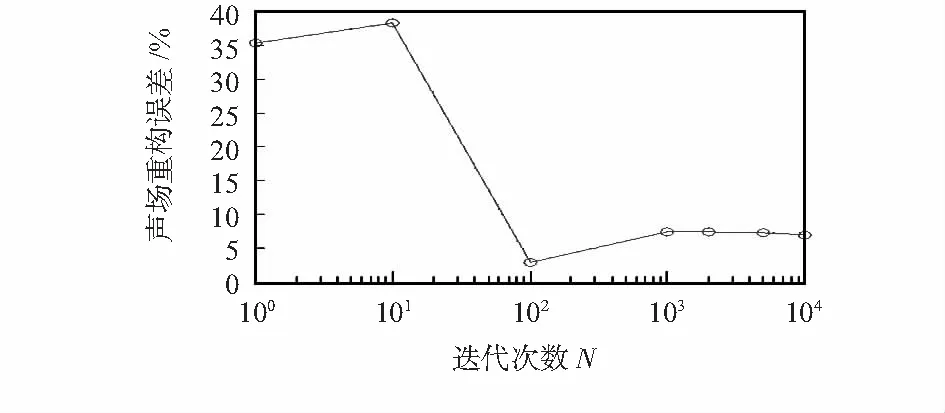
图5 迭代次数对声场重构的影响

在迭代次数选择2 000时，计算分析了不同全息面数据补零长度对声场重构的影响，具体如图6所示。可以发现：随着补零长度的增加，声场重构误差逐步减小，当全息面补零长度为原始测量数据长度的2.5倍后，声场重构误差基本趋于稳定；在实际工程中，选择全息面补零至原始数据长度的2倍即可。

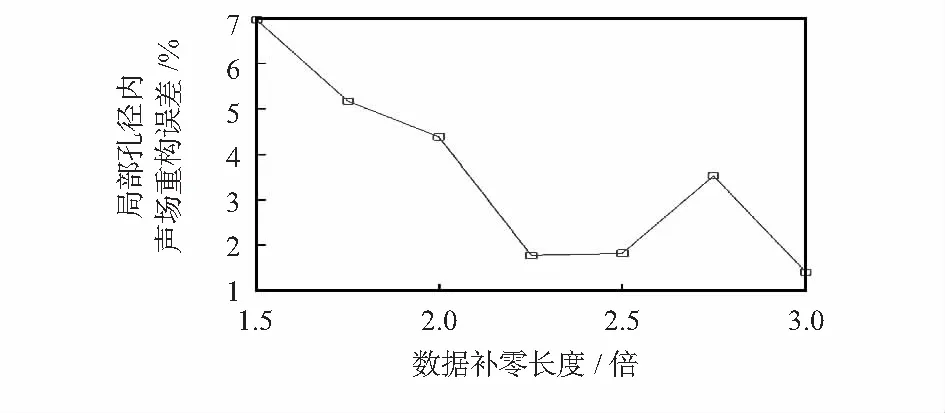
图6 数据补零长度对声场重构的影响

4 试验分析

使用转子台作为被测设备，模拟机械设备故障，在有限孔径的测量条件下，验证基于“有限孔径空间扩展+波数域迭代滤波”的声全息算法在实际声全息测试中的适用性。

如图7所示，转子台主要组成部件为两个轴承及一个连接杆，通过主控机箱可以控制轴承启动、停止，并能够调节转速。通过调整，可使转子台模拟出偏心、磨碰、松动、油膜振荡等多种故障。通过全息测试与分析定位故障位置，并对该位置数据进行进一步分析。

图7 转子台

试验中使用20只麦克风组成一个4行5列的矩形面阵，麦克风横向和纵向间隔皆为0.2m，阵列距转子台距离为0.15m。图8为故障类型为偏心时的测试分析结果。(a)和(b)为分析频率为58Hz时的全息面声压分布与重构声压分布，(c)和(d)为分析频率为230Hz时的全息面声压分布与重构声压分布，在两个分析频率下，全息面声压分布皆呈现边缘能量较强的情况，为典型的有限孔径现象，通过变换后，在重构结果中能够明显定位出噪声亮点，并与产生故障的空间位置对应，可见通过全息变换能够定位噪声源的位置，形成声场分布。

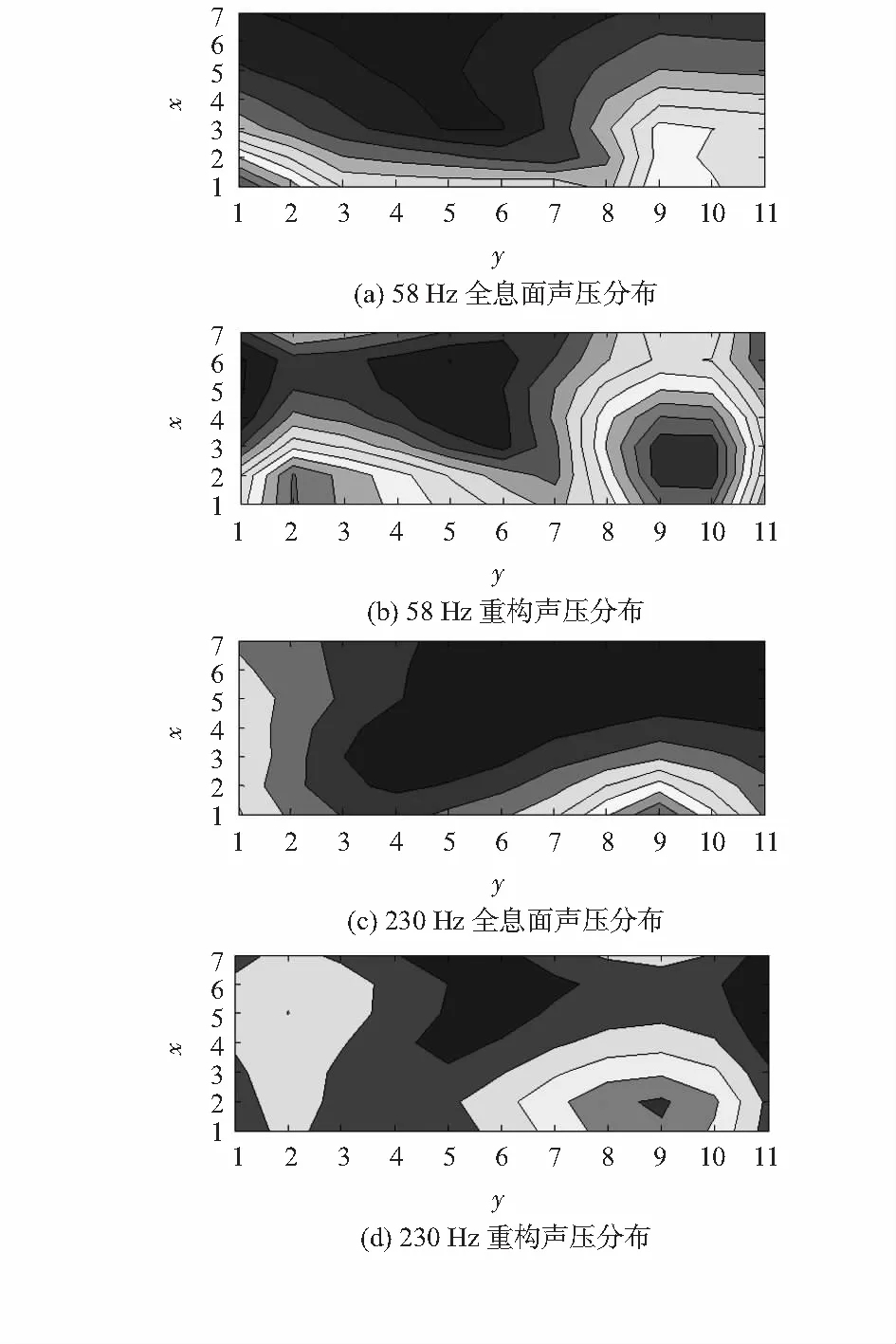
图8 不同分析频率时的全息面声压与重构声压分析

5 结 论

以基于空间声场变换的近场平面声全息算法为基础，对在该算法应用中重构误差产生机理及解决方法开展了系统的研究，提出了利用“有限孔径空间扩展+波数域迭代滤波”声全息算法消除截断误差的方法，选用简谐激励作用下四周为无限大障板的简支钢板为对象，验证了算法的准确性，并分析了全息面数据空间补零长度和迭代循环次数对声场重构的影响；并以转子台作为被测目标对算法进行了试验验证，取得了较为理想的效果。因此，将本文方法应用于有限孔径测试条件下的声全息重构中有效、可行。

[1]MaynardJD,WilliamsEG,LeeY.NearfieldacousticalholographyI:TheoryofgeneralizedholographyandthedevelopmentofNAH[J].JournaloftheAcousticalSocietyofAmerica,1985,78(4):1395-1413.

[2]WilliamsEG,HoustonBH,HerdicPC.FastFouriertransformandsingularvaluedecompositionformulationsforpatchnearfieldacousticalholography[J].JournaloftheAcousticalSocietyofAmerica,2003,114(3):1322-1333.

[3]WilliamsEG.ApproachestopatchNAH[C]∥Inter-Noise,Jeju,Korea,2003:2187-2194.

[4]XuL,BiCX,ChenXZ.Applicationofpapoulis-gerchbergalgorithminpatchnear-fieldacousticholography[C]∥Inter-Noise,Shanghai,China,2008:2330～2337.

[5] 徐 亮，毕传兴，陈 剑，等.基于波叠加法的Patch近场声全息及其实验研究[J].物理学报,2007,56(5):2776-2783.

[6]WilliamsEG,MaynardJD.NumericalevaluationoftheRayleighintegralforplanarradiatorsusingtheFFT[J].JournaloftheAcousticalSocietyofAmerica,1982,72(6):2020-2030.

[7]VeronesiWA，MaynardJD.Near-fieldacousticholography(NAH)II.holographicrecon-structionalgorithmsandcomputerimplemenfion[J].JAcoustSocAm,1987，81(5)：1307-1322.

刘 超，通讯作者，E—mail:woaiwenzi510@163.com。

Research on holographic measurement and analysis method based on new type sensor array

CHEN Yun-feng1, LIU Chao2, LÜ Yao-hui3

(1.Navy Military Representative Office in Wuxi Area, Wuxi 214061,China；2.Haiying Enterprise Group Co Ltd，Wuxi 214000,China;3.Institute of Acoustics, Chinese Academy of Sciences,Beijing 100190,China)

Aiming at problem of the scanning phase error and the limited measurement aperture in the practical engineering application,propose two methods to analyze and solve the issues above,which are improved test array and algorithm optimization,using the method of snapshot measurement based on the plane array with digital microphones,instead of the traditional scanning measurement,the phase error is avoided,the limited aperture near-field acoustical holography reconstruction error mechanism are analyzed in theory,A new method of acoustical holography named "limited aperture space extension + wavenumber domain iterative filtering" are proposed.Take a simply-supported infinite steel plate that under harmonic excitation as example,compare with the result from the conventional near-field acoustic holography,demonstrate the effectiveness of the algorithm,analyze on influence of the "0" space range and the number of iterations on the reconstructing of the acoustic field.The rotor testbed is used as the device under test,The known fault is simulated by the rotor table.The applicability of the algorithm is verified by the scanning result of the sensor array with a single reference sensor.The simulation fault location is located accurately.

near-field acoustical holography ; digital microphone; plane array;limited aperture; wave number domain filtering; iteration

10.13873/J.1000—9787(2017)08—0055—04

2016—12—02

TB 52

A

1000—9787(2017)08—0055—04

陈允锋(1976-)，男，硕士，工程师，研究方向为数字信号处理。