光子石墨烯中赝磁场作用下的谷霍尔效应∗

邓富胜1)2)3)† 孙勇4) 刘艳红1)2)3) 董丽娟1)2)3) 石云龙1)2)3)

1)(山西大同大学固体物理研究所,大同 037009)

2)(山西大同大学,微结构电磁功能材料省市共建山西省重点实验室,大同 037009)

3)(山西大同大学,新型微结构功能材料山西省高等学校重点实验室,大同 037009)

4)(同济大学,先进微结构材料教育部重点实验室,上海 200092)

光子石墨烯中赝磁场作用下的谷霍尔效应∗

邓富胜1)2)3)† 孙勇4) 刘艳红1)2)3) 董丽娟1)2)3) 石云龙1)2)3)

1)(山西大同大学固体物理研究所,大同 037009)

2)(山西大同大学,微结构电磁功能材料省市共建山西省重点实验室,大同 037009)

3)(山西大同大学,新型微结构功能材料山西省高等学校重点实验室,大同 037009)

4)(同济大学,先进微结构材料教育部重点实验室,上海 200092)

(2017年3月1日收到;2017年4月16日收到修改稿)

将石墨烯中赝磁场的产生机理运用于光子石墨烯,通过在光子石墨烯中引入晶格有规律单轴形变的方式,理论分析得到了谷依赖的均匀赝磁场,并通过数值模拟的方法观察到明显的谷霍尔效应.这种谷霍尔效应的显著程度随晶格形变度的增加而加强.在具有一定损耗的电介质材料构成的形变光子石墨烯中仍可观察到明显的谷霍尔效应.随着电介质材料损耗的增加,谷霍尔效应导致的波束转弯效果依然能够保持,只是强度逐渐变弱.类似于自旋电子学中的自旋霍尔效应,这种光子石墨烯中等效赝磁场作用下的谷霍尔效应在未来谷极化器件的设计和应用中具有重要意义.

光子晶体,光子石墨烯,赝磁场,谷霍尔效应

1 引 言

石墨烯的能带在第一布里渊区的六个拐角(或K点)处上下能带简并形成的圆锥形奇点称为狄拉克点[1].在该点附近对应两个亚格子,形成两个不等价的狄拉克锥,也称作谷.由于缺乏短程相互作用,这两个在动量空间中分离的不等价的谷形成类似自旋的谷自由度,也称作赝自旋.2007年,Xiao等[2]发现在空间反演对称性破缺的石墨烯的两个不等价的谷具有类似于电子自旋中玻尔磁子的本征磁矩.这使得谷自由度成为一个可直接测量的物理量.实际上,石墨烯在合适的面内电场或磁场作用下,不同谷中的电子在垂直于入射面的横向相互分离,造成不同谷中电子束向相反方向偏转,这种现象叫做谷霍尔效应,类似于自旋霍尔效应.这里不等价的谷扮演自旋电子的角色.

近年来,基于石墨烯及类似二维材料的谷霍尔效应已经成为一个新的研究热点[2-4].例如,2014年,Mak等[3]在类似于石墨烯的单层二硫化钼晶体结构中也观察到了这种奇特的谷霍尔效应.二硫化钼的晶格及能带结构与石墨烯类似,但有所不同.这类材料中组成蜂窝状晶格的两个亚格子不同(分别对应S和Mo原子),导致其能带结构在布里渊区拐角处的带隙被打开.由于这种直接带隙半导体材料晶体结构的反演对称性被打破,因此不同谷中电子将会受到大小相等、方向相反的有效磁场的作用,进而可以观察到谷霍尔效应[3].在该工作基础上,2015年,南京师范大学张力发教授与美国德克萨斯大学Qian Niu教授合作,在声子体系下理论研究了二硫化钼类比物的手征特性及谷霍尔效应[4].2016年,刘正猷教授课题组在声子体系下,首先理论模拟研究了谷依赖的涡旋态[5].最近,该课题组在此工作基础上又进一步实验观察到了类似于凝聚态体系中拓扑霍尔边界态[6-8]的新奇物理现象及随入射角变化的谷霍尔效应[9].

另外,由于石墨烯的厚度仅相当于一个原子层,因此很容易受外界影响,譬如易发生机械形变.若石墨烯上外界应力引起的平滑渐变的机械形变在原子间距尺度上,则不会破坏石墨烯亚格子对称性,但会使得布里渊区发生扭曲,从而使石墨烯两个谷(K和K′点)中电子向相反方向移动[10-17].这类似于电子在磁场作用下的运动.合适的机械应变会在石墨烯中产生均匀的赝磁场,且对两个谷具有相反符号.这种机械形变引起的赝磁场不同于外加磁场,不会破坏结构的时间反演对称性,因而提供了一种崭新的不需要外场便可控制电子行为的机理.

近年来,基于光子与电子作为波的共性,人们开始研究与石墨烯具有相同对称性、相似能带结构的光子晶体.通常,具有三角晶格或者蜂窝晶格的光子晶体,由于其能带在第一布里渊区拐角处同样存在狄拉克点,且在该点附近对应两个亚格子形成两个不等价的谷,这样的光子晶体称作光子石墨烯(photonic graphene,PG)[18-23].在光子体系下,已有学者在形变光子石墨烯结构中观察到了赝磁场和朗道量子化效应[24]以及类似朗道能级引起的光的放大态[25].而且,光子石墨烯中谷依赖电磁波的输运行为及人工赝磁场相关新奇物理现象的研究,已经取得了一些新的进展[26-28].如何实现基于光子石墨烯的谷霍尔效应,能否获得不需要任何外场作用的谷霍尔效应,这些问题仍然未知.

本文通过在光子石墨烯中引入晶格有规律的单轴形变的方式,理论分析获得了谷依赖的均匀赝磁场.通过数值模拟的方法观察到了明显的人工赝磁场作用下的谷霍尔效应.这种谷霍尔效应的显著程度随晶格形变度的增加而加强.我们还针对组成形变光子石墨烯的电介质材料,考虑不同程度吸收情况下谷霍尔效应导致的谷依赖的波束转弯行为,作了进一步模拟计算和讨论.光子石墨烯中这种等效赝磁场作用下的谷霍尔效应,类似于自旋电子学中的自旋霍尔效应,具有潜在应用价值.

2 光子石墨烯中谷依赖的均匀赝磁场

光子晶体能带通常用平面波展开法计算,有时也在Wannier表像下描述其哈密顿量[29,30].在 Wannier表像下,我们引入参数βij表示相邻位置i与j间的耦合系数,

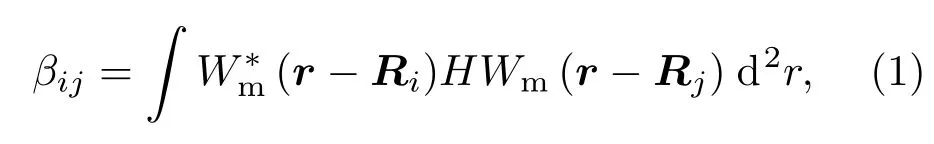
式中Wm(r-Rj)称为Wannier函数,它是以格点Rj为中心的局域函数.其中r是空间坐标,Rj是格点坐标,H是等价的哈密顿量.如图1(a)所示,采用的光子石墨烯是由亚格子A和B组成的蜂窝状结构.考虑最近邻和次近邻近似,Wannier表像下的哈密顿量类似于紧束缚近似下石墨烯的哈密顿量[1],可表示为

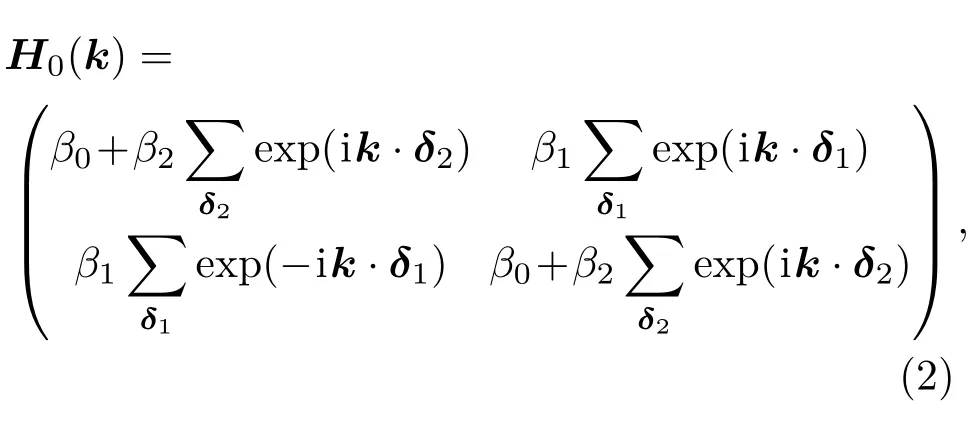
式中β0,β1,β2分别为原位能(on-site energy)、最近邻耦合系数和次近邻耦合系数,k为波矢.δ1(δ2)为最近邻(次近邻)位移矢量(图1(a)).哈密顿量对应的本征值为ω2(k)/c2.图1(b)所示为规则光子石墨烯在微波段的三维能谱图,在该能谱中对应于两个亚格子存在两个不等价的谷.

图1 (网刊彩色)结构模型与能带 (a)蜂窝状光子石墨烯结构示意图;(b)规则光子石墨烯对应三维能带图Fig.1.(color online)Model and energy band：(a)The model for the photonic graphene with honeycomb lattice;(b)three-dimensional energy band of the photonic graphene.

对于晶格扭曲的光子石墨烯,应变会改变其介电常数ε(r)的分布,从而与石墨烯中的情况类似,局部改变β1的值.为了研究这种应变效应,我们采用与电子石墨烯相同的做法.按照有关形变石墨烯的描述[10-12],对于晶格扭曲的石墨烯,在其狄拉克点附近的哈密顿量H0(k)需要增加新的一项,可写为

式中σ=(σx,σy)为泡利矩阵,A为规范矢势,

式中κ =-∂lnβ1/∂lna为无量纲参数;uij为应变张量,定义为例如uyy=∂uy/∂y;符号±分别对应由时间反演对称性相联系的K与K′两个不等价的谷.因此,赝磁场为BK=-BK′=∇×A.

为获得等效均匀赝磁场,选用的单轴应变张量为

按照这种应变方式,在这种单轴扭曲的光子石墨烯中赝磁场BK=-BK′,且|BK=|-BK′=κc0/a是一个常数,c0为形变系数.因此,通过在光子石墨烯中引入这种特定的单轴形变,理论上可以获得谷依赖的均匀赝磁场.

3 光子石墨烯中赝磁场作用下的谷霍尔效应

为了进一步观察赝磁场作用下的谷霍尔效应,我们按照实际蜂窝状晶格的排布规律根据(5)式设计了具体的晶格距离渐变的结构模型.图2为这种晶格形变的光子石墨烯模型(图2(b))与规则石墨烯模型(图2(a))的对比.晶格扭曲沿y方向,发生形变的亚格子A和B所在位置的空间坐标遵循如下规律：

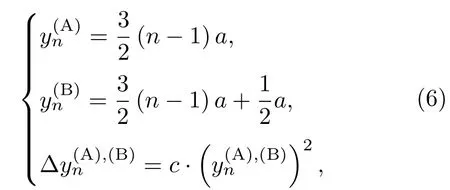
图3(a)为得到的规则光子石墨烯对应二维能谱结构示意图.这里组成光子石墨烯的电介质柱子半径和介电常数分别为1.5 mm和9,最近邻柱子间距离为a=6 mm.该能谱中前两个带在K点处简并(10.73 GHz),形成狄拉克点.图中红色虚线对应位置处于能带三角扭曲区域(9.40 GHz).对于规则光子石墨烯而言(图3(b)),在Zigzag界面处能带的三角扭曲效应会引起谷依赖的分束现象[31].分开的两波束分别对应光子石墨烯两个不等价的谷(K和K′点).图3(b)插图中半圆形与三角形分别为空气与光子石墨烯中的等频线(9.40 GHz),由于群速度方向始终垂直于等频线,因而可以形成夹角约为60°的劈裂波束.根据前文理论分析,单轴扭曲情况下晶格应变量与坐标满足二次方关系时,可以在光子石墨烯中产生均匀的赝磁场.因此,在这种晶格扭曲的光子石墨烯中预期可以观察到赝磁场作用下的谷霍尔效应.即石墨烯在赝磁场作用下,两个不等价谷中的光子在垂直于入射面的横向相互分离,故可观察到谷依赖的波束弯曲效应.

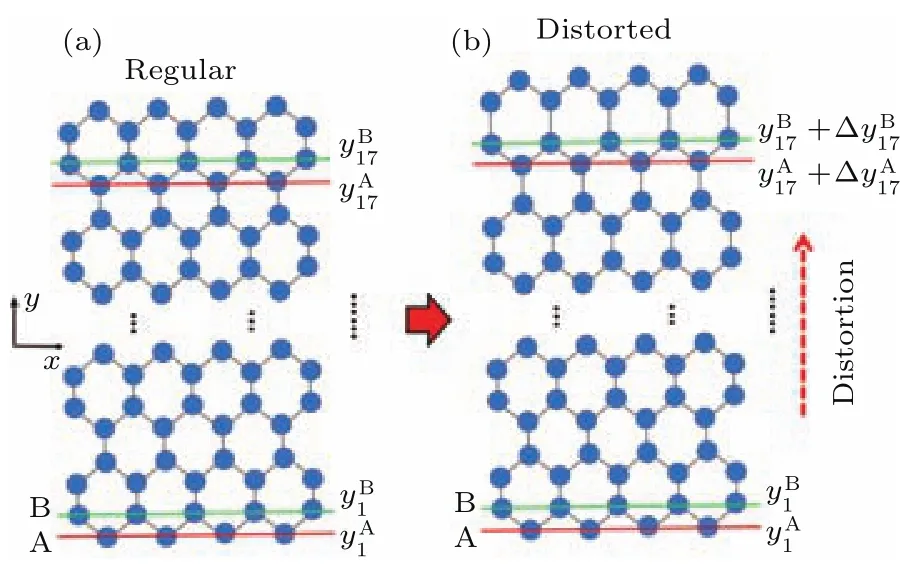
图2 (网刊彩色)(a)规则光子石墨烯示意图;(b)单轴扭曲光子石墨烯示意图Fig.2.(color online)(a)Schematic of regular PG; (b)schematic of uniaxially distorted PG.

图3 (网刊彩色)能带图及谷依赖分束示意图 (a)规则光子石墨烯二维能带结构示意图;(b)能带三角扭曲效应引起的谷依赖分束示意图Fig.3.(color online)Schematic of 2D energy band and valley dependent beam splitting e ff ect：(a)2D energy band for regular PG;(b)valley dependent beam splitting e ff ect in regular PG.

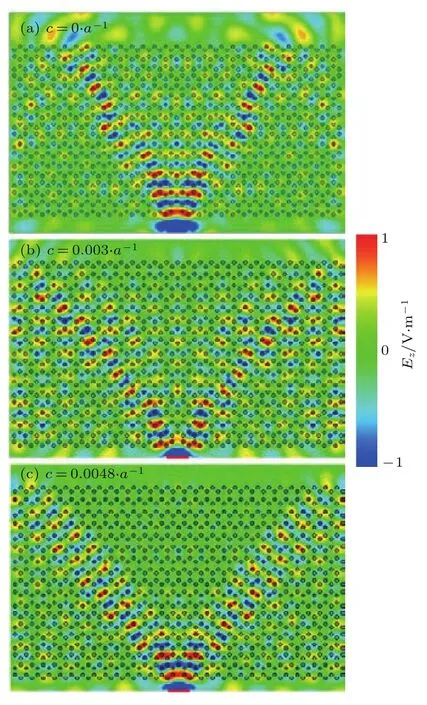
图4 (网刊彩色)单轴扭曲的光子石墨烯结构中赝磁场作用下的谷霍尔效应 (a)规则结构在9.4 GHz处的模拟结果;(b)扭曲度为c=0.003·a-1的单轴扭曲光子石墨烯结构在9.4 GHz处的模拟结果;(c)扭曲度为c=0.0048·a-1的单轴扭曲光子石墨烯结构在9.4 GHz处的模拟结果Fig.4.(color online)Valley Hall effect induced by pseudomagnetic field in uniaxially distorted photonic graphene：(a)Simulated 2D electric field distribution for regular PG at 9.4 GHz;(b)simulated 2D electric field distribution for distorted PG(c=0.003·a-1)at 9.4 GHz;(c)simulated 2D electric field distribution for distorted PG(c=0.0048·a-1)at 9.4 GHz.

我们通过电磁仿真软件观察这种赝磁场作用下的谷霍尔效应.数值仿真采用三维高频电磁场仿真软件(CST,Computer Simulation Technology公司,德国),选择时域求解器模块进行计算.波源采用波导端口,其中端口大小可任意调节,入射波为高斯脉冲.边界条件设置如下：沿电介质柱子轴的方向为电边界(相当于金属壁),垂直于电介质柱子轴的方向为开放边界(背景为空气).为了进行对比分析,同时模拟计算了规则光子石墨烯中波束传输的电场分布.图4(a)为规则光子石墨烯中9.4 GHz频率处二维电场分布的模拟计算结果,从图中可以清楚观察到谷依赖的波束劈裂现象.图4(b)是对扭曲度为c=0.003·a-1的单轴扭曲光子石墨烯结构得到的模拟计算结果,从图中可以明显看出波束的弯曲效应,而且劈裂的不同谷的波束沿相反的弯曲路径传播,有明显的谷霍尔效应产生.图4(c)是对扭曲度为c=0.0048·a-1的单轴扭曲光子石墨烯结构得到的模拟计算结果.与图4(b)相比,此时光子石墨烯波束转弯效果更为明显,而且两束波之间的场强很弱,相当于随着扭曲度的增加,赝磁场作用逐渐增强,谷霍尔效应变得更为清楚.

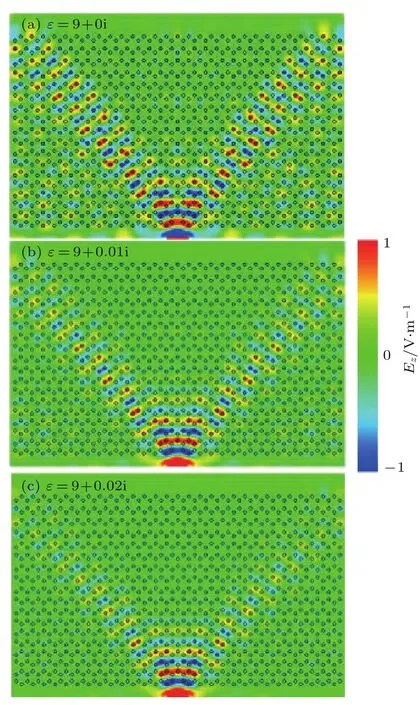
图5 (网刊彩色)扭曲度为c=0.0048·a-1的光子石墨烯电介质材料在不同介电常数ε取值情况下的电场分布(a)ε=9+0i;(b)ε=9+0.01i;(c)ε=9+0.02iFig.5.(color online)Simulated 2D electric field distribution for distorted PG(c=0.0048·a-1)with different dielectric constants ε：(a)ε=9+0i;(b)ε= 9+0.01i;(c)ε=9+0.02i.

仿真计算时没有考虑材料的损耗.为了使数值计算结果更贴近实际,我们在材料中引入不同程度的损耗,进一步对扭曲度为c=0.0048·a-1的单轴扭曲光子石墨烯结构进行模拟计算.如图5所示,图5(a)—图5(c)中电介质材料介电系数分别取ε=9+0i,ε=9+0.01i,ε=9+0.02i时对应的仿真结果.从对比结果可知,随着电介质材料损耗(介电系数虚部)的增加,依然能够保持波束转弯效果,只是强度逐渐变弱.该结果表明在具有吸收或损耗的实际电介质材料构成的形变光子石墨烯中仍然可以观察到明显的谷霍尔效应.

4 结 论

本文主要借鉴电子石墨烯中非均匀机械应力作用下产生赝磁场的机理,在单轴扭曲的光子石墨烯中观察到了赝磁场作用下的谷霍尔效应.这种晶格扭曲的光子石墨烯结构的时间反演对称性没有被破坏,两个谷中的光子受到大小相等、方向相反的赝磁场作用.因此,两个谷中光子束在这种赝磁场作用下将沿不同的弯曲路径运动,这类似于石墨烯在面内电场作用下或二硫化钼在有效磁场作用下的谷霍尔效应.该结果揭示了这种人工赝磁场对光子束谷依赖的调控能力.随着集成光路技术的不断发展,这种人工磁场控制下的波束传输机理对于集成化光学器件的研制和应用具有重要意义.

[1]Neto A C,Guinea F,Peres N M,Novoselov K S,Geim A K 2009 Rev.Mod.Phys.81 109

[2]Xiao D,Yao W,Niu Q 2007 Phys.Rev.Lett.99 236809

[3]Mak K F,McGill K L,Park J,McEuen P L 2014 Science 344 1489

[4]Zhang L,Niu Q 2015 Phys.Rev.Lett.115 115502

[5]Lu J,Qiu C,Ke M,Liu Z 2016 Phys.Rev.Lett.116 093901

[6]Ju L,Shi Z,Nair N,Lv Y,Jin C,Velasco J Jr,Ojeda-Aristizabal C,Analytis J,Wang F 2015 Nature 520 650

[7]Li J,Wang K,McFaul K J,Zern Z,Ren Y,Watanabe K,Taniguchi T,Qiao Z,Zhu J 2016 Nature Nano.11 1060

[8]Yin L J,Jiang H,Qiao J B,He L 2016 Nature Commun. 7 11760

[9]Lu J,Qiu C,Ye L,Fan X,Ke M,Zhang F,Liu Z 2017 Nat.Phys.13 369

[10]Ken-ichi S,Yoshiyuki K,Riichiro P S 2005 Theor.Phys. 113 63

[11]Guinea F,Katsnelson M I,Geim A K 2010 Nat.Phys. 6 30

[12]Levy N,Burke S A,Meaker K L,Panlasigui M,Zettl A, Guinea F,Castro Neto A H,Crommie M F 2010 Science 329 544

[13]Wu Z,Zhai F,Peeters F M,Xu H Q,Chang K 2011 Phys.Rev.Lett.106 176802

[14]Jiang Y,Low T,Chang K,Katsnelson M I,Guinea F 2013 Phys.Rev.Lett.110 046601

[15]Zhang D,Seifert G,Chang K 2014 Phys.Rev.Lett.112 096805

[16]Guinea F,Geim A K,Katsnelson M I,Novoselov K S 2010 Phys.Rev.B 81 035408

[17]Low T,Guinea F 2010 Nano Lett.10 3551

[18]Zandbergen S R,de Dood M J A 2010 Phys.Rev.Lett. 104 043903

[19]Plotnik Y,Rechtsman M C,Song D,Heinrich M,Zeuner J M,Nolte S,Lumer Y,Malkova N,Xu J,Szameit A, Chen Z,Segev M 2013 Nat.Mater.13 57

[20]Rechtsman M C,Plotnik Y,Zeuner J M,Song D,Chen Z,Szameit A,Segev M 2013 Phys.Rev.Lett.111 103901

[21]Zeuner J M,Rechtsman M C,Nolte S,Szameit A 2014 Opt.Lett.39 602

[22]Crespi A,Corrielli G,Valle G D,Osellame R,Longhi S 2013 New J.Phys.15 013012

[23]Wang X,Jiang H T,Yan C,Sun Y,Li Y H,Shi Y L, Chen H 2013 Europhys.Lett.103 17003

[24]Rechtsman M C,Zeuner J M,Tünnermann A,Nolte S, Segev M,Szameit A 2013 Nat.Photon.7 153

[25]Schomerus H,Halpern N Y 2013 Phys.Rev.Lett.110 013903

[26]Deng F S,Sun Y,Wang X,Xue R,Li Y,Jiang H T,Shi Y L,Chang K,Chen H 2014 Opt.Express 22 23605

[27]Deng F,Sun Y,Dong L,Liu Y,Shi Y 2017 J.Appl. Phys.121 074501

[28]Deng F S,Li Y M,Sun Y,Wang X,Guo Z W,Jiang H T,Shi Y L,Chang K,Chen H 2015 Opt.Lett.40 3380

[29]Albert J P,Jouanin C,Cassagne D,Monge D 2002 Opt. Quant.Electron.34 251

[30]Wol ffC,Mack P,Busch K 2013 Phys.Rev.B 88 075201

[31]Garcia-Pomar J L,Cortijo A,Nieto-Vesperinas M 2008 Phys.Rev.Lett.100 236801

PACS:42.70.Qs,41.20.Jb,42.25.Bs DOI:10.7498/aps.66.144204

Valley Hall e ff ect induced by pseudomagnetic field in distorted photonic graphene∗

Deng Fu-Sheng1)2)3)†Sun Yong4)Liu Yan-Hong1)2)3)Dong Li-Juan1)2)3)Shi Yun-Long1)2)3)
1)(Institute of Solid State Physics,Shanxi Datong University,Datong 037009,China)
2)(Shanxi Provincial Key Laboratory of Microstructure Electromagnetic Functional Materials,Shanxi Datong University, Datong 037009,China)
3)(Key Laboratory of New Microstructure Function Materials in Shanxi Province,Shanxi Datong University, Datong 037009,China)
4)(Key Laboratory of Advanced Microstructure Materials,Ministry of Education,Tongji University,Shanghai 200092,China)

1 March 2017;revised manuscript

16 April 2017)

Like the spin in spintronics,the valley index in graphene can be viewed as a new carrier of information,which is useful for designing modern electronic devices.Recently,we have applied the concept of valleytronics to photonic graphene,revealed valley-dependent beam splitting e ff ect and realized pseudomagnetic field.The pseudomagnetic field enables a novel manipulation of photons.In this paper,the photonic analogy of valley Hall e ff ect in uniaxially distorted photonic graphene is investigated.It is found that photons in two valleys are subjected to pseudomagnetic fields that are equal in strength but opposite in sign.With the increasing of distortion,the valley Hall e ff ect becomes stronger. In addition,it is found that the photonic valley Hall e ff ect can still be maintained under the in fl uence of loss,although the beam intensity decreases.The photonic analogy of valley Hall e ff ect induced by pseudomagnetic field in uniaxially distorted photonic graphene may be very useful for controlling the fl ow of light in future valley-polarized devices.

photonic crystal,photonic graphene,pseudomagnetic field,valley Hall e ff ect

:42.70.Qs,41.20.Jb,42.25.Bs

10.7498/aps.66.144204

∗国家自然科学基金(批准号：11604186,11674247,11504211)、山西省自然科学基金(批准号：201601D202011)、山西省科技攻关项目(批准号：2015031002-2)和大同市科技攻关项目(批准号：2016021,2015015,201308)资助的课题.

†通信作者.E-mail：dengfusheng2005@163.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11604186,11674247,11504211),the Natural Science Foundation of Shanxi Province,China(Grant No.201601D202011),the Science and Technology Project of Shanxi Province,China(Grant No.2015031002-2),and the Science and Technology Project of Datong,Shanxi Province, China(Grant Nos.2016021,2015015,201308).

†Corresponding author.E-mail：dengfusheng2005@163.com