某商用车变速器传动效率偏低原因分析及改进

陈德鑫 陈曦 孙友情 杨启 石兴磊

（中国第一汽车股份有限公司技术中心，长春 130011）

某商用车变速器传动效率偏低原因分析及改进

陈德鑫 陈曦 孙友情 杨启 石兴磊

（中国第一汽车股份有限公司技术中心，长春 130011）

以某变速器在产品开发过程中遇到的传动效率偏低问题为例，通过与对标样件试验数据对比分析，确定与载荷相关的损失偏大是导致该变速器效率偏低的主要因素。建立齿轮和轴承功率损失的数学模型，从齿轮参数及轴承选型的角度分析该变速器效率偏低的原因。利用遗传算法对齿轮参数进行优化设计，并更改轴承类型。改进后的试验结果表明，变速器效率提高了0.55%～0.70%，达到了对标变速器的效率水平。

1 前言

变速器传动效率的正向设计开展较少，工程实践中经常会出现效率偏低的现象。在传动效率研究方面，王治平等人[1]建立了考虑扭矩、转速、速比及油温等因素的变速器传动效率半经验公式，王熙等人[2]建立了乘用车变速器传动效率的理论分析模型，但其并没有对影响变速器传动效率的内部因素进行分析。

本文以某变速器开发过程中出现的效率偏低问题为例，通过与对标样箱传动效率试验数据的对比分析，确定引起该变速器效率偏低的主要因素，建立传动效率数学模型，从齿轮参数及轴承选型的角度分析该变速器效率偏低的原因，并提出改进方案。

2 变速器传动效率试验

2.1 变速器基本信息

变速器A为新开发样机，是在现有变速器B的基础上为改善NVH性能而进行的升级换代，升级换代后变速器A的重合度明显大于变速器B，其中1挡、2挡齿轮重合度分别由1.5、2.2增大到1.7、2.8，其余挡位齿轮由2.3增大到3.2，并且齿轮的弯曲疲劳和接触疲劳寿命普遍提高10%～20%。为了进行效率对比评价，引入对标变速器C，该变速器由国外某知名公司生产，为同类别中国际领先产品。3种变速器均为三段式平行轴结构，如图1所示。以4挡为例，变速器的动力传递路线需要经过常啮合齿轮（1、4）和4挡挡位齿轮（5、14）两对齿轮。所匹配发动机的最大扭矩（转速）为700 N·m（1 500 r/min）。

2.2 试验方法

对3种变速器分别进行台架效率试验。在变速器的输入及输出端各安装一个扭矩传感器，并分别连接测功机，润滑油油温控制在80±2℃范围内，进行稳态工况试验。为了保证测试精度，测试扭矩应保证在扭矩传感器满量程的75%～100%使用，测试扭矩与扭矩传感器量程不匹配时，需更换扭矩传感器。扭矩传感器精度要求为0.2%F.S.[3]。变速器的传动效率：

式中，Po为输出功率；Pi为输入功率；To为输出扭矩；Ti为输入扭矩；no为输出转速；ni为输入转速。

图1 变速器结构示意

对于手动机械式变速器，传动效率可通过输入扭矩损失ΔT表示[4]：

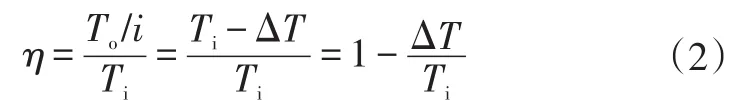
式中，i为速比。

2.3 试验结果

采用在油温80℃，所匹配发动机最大扭矩及对应转速工况下各挡效率作为变速器传动效率的评价点[5]。图2为除5挡(直接挡)外，各挡效率的试验对比结果。可知，对标变速器C的效率最高；变速器A的效率比变速器B低0.3%～0.4%，比变速器C低0.5%～0.7%。

图2 变速器传动效率试验结果

2.4 影响因素分析

机械式变速器可通过ΔT来评价效率的高低。根据试验测试结果，在转速一定的条件下，ΔT与Ti可拟合为如图3所示的线性关系，拟合优度系数R2均在0.99以上。ΔT可分为两部分，其中ΔTP为与载荷无关的损失（如齿轮、轴承等回转体的搅油损失，油封和同步器等回转体的摩擦损失），ΔTL为与载荷相关的损失（如轴承、齿轮等在传递扭矩时的摩擦损失），其随输入载荷的增大而增大。

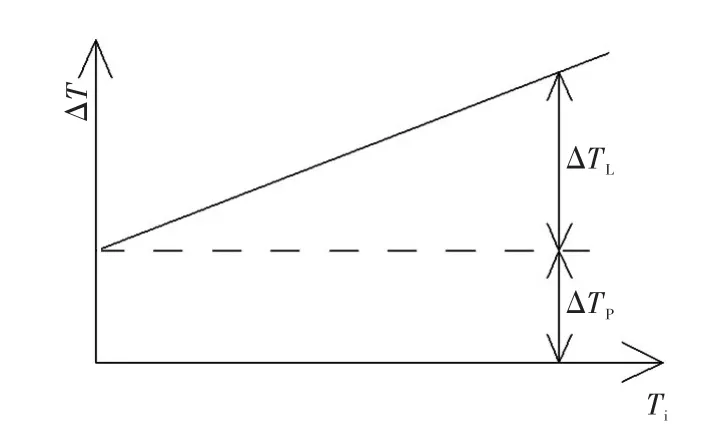
图3 扭矩损失与输入扭矩的关系

图4为在1 500 r/min工况下，变速器各挡位输入扭矩损失的对比结果。与载荷无关的损失中，变速器C比变速器A和B略大，但随着载荷的增大，变速器A和B扭矩损失的增幅程度均大于变速器C，即变速器A的斜率最大，变速器B其次，变速器C最小。因此，与载荷相关的因素是导致换代变速器A传动效率偏低的主要因素。

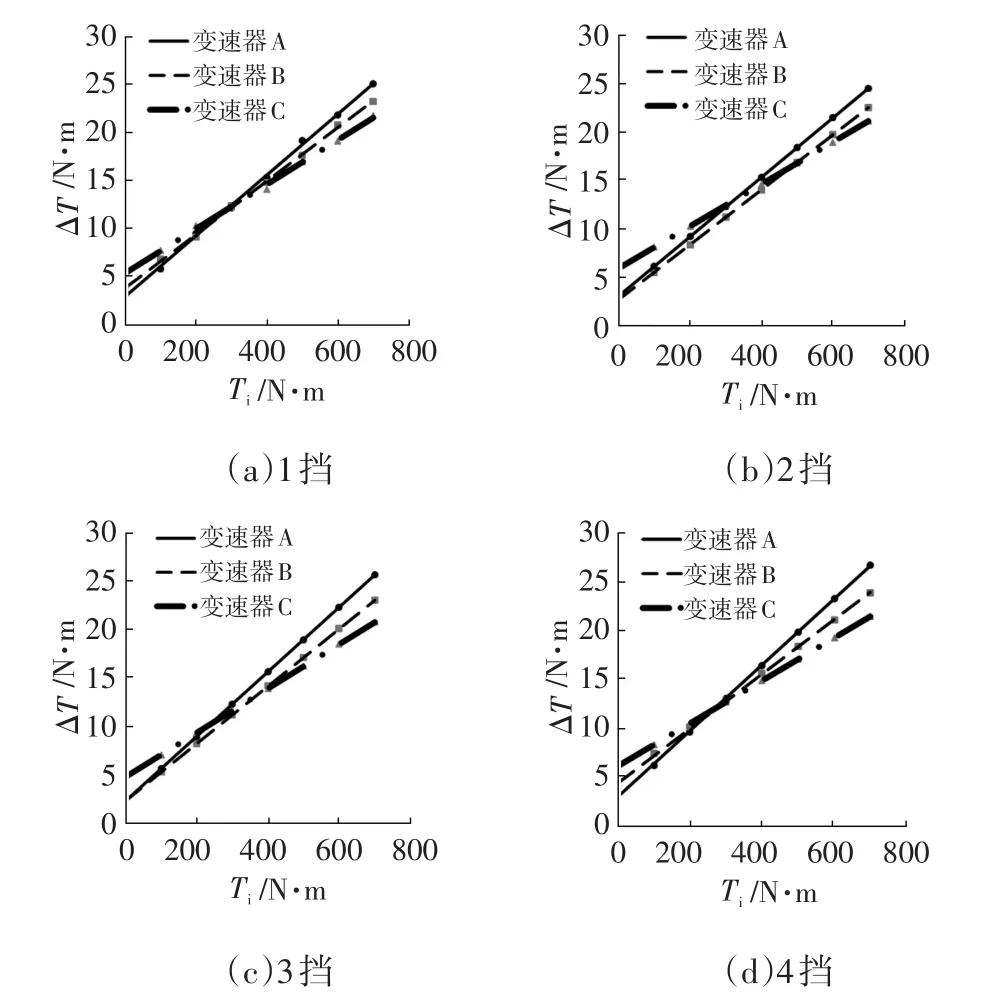
图4 变速器输入扭矩损失对比结果（1 500 r/min）

3 变速器损失的数学模型

为分析变速器中与载荷相关的损失，分别建立齿轮啮合损失及轴承摩擦损失的数学模型。

3.1 齿轮啮合损失数学模型

单对齿轮啮合的滑动摩擦功率损失Pg为[6]：

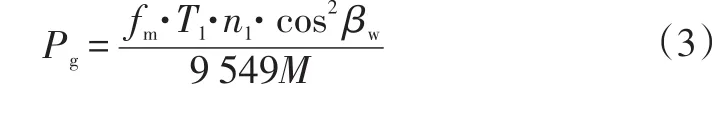
其中，

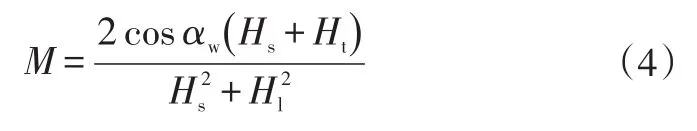
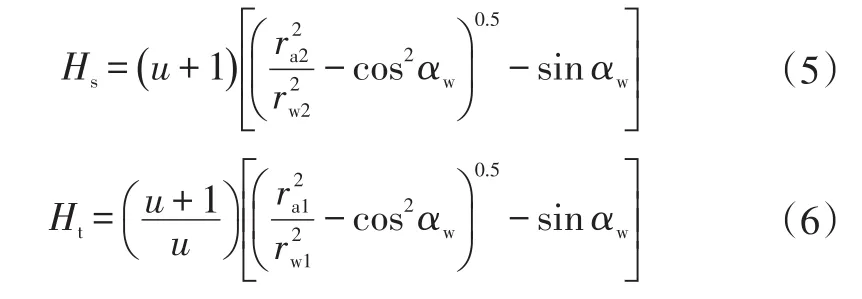
式中，fm为啮合摩擦系数，该处用平均滑动摩擦系数代替，混合润滑状态下取0.04[7]；T1为主动齿轮扭矩；n1为主动齿轮转速；βw为节圆螺旋角；αw为节圆端面啮合角；u为从动齿轮与主动齿轮的齿数比；ra1、ra2分别为主动齿轮和从动齿轮齿顶圆半径；rw1、rw2分别为主动齿轮和从动齿轮的节圆半径。

3.2 轴承摩擦损失数学模型

深沟球轴承摩擦功率损失Pb为[6]：

圆柱滚子轴承摩擦损失P′b为：

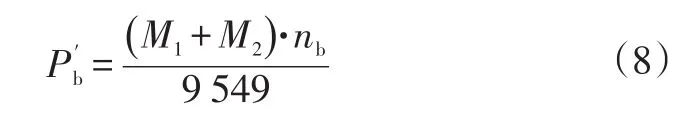
其中，

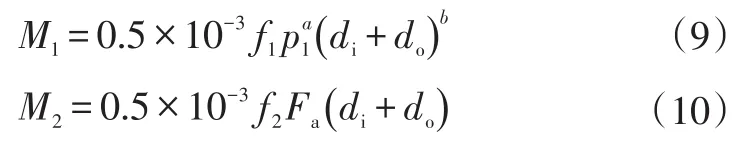
式中，P1为轴承动载荷，深沟球轴承P1=3Fa-0.1Fr，圆柱滚子轴承P1=Fr；Fa为轴承的轴向载荷分量；Fr为轴承的径向载荷分量；nb为轴承转速；f1和f2为摩擦系数；di为轴承内径；do为轴承外径；a为载荷修正指数，b为直径修正指数，除调心滚子轴承外，a和b均取1。

4 齿轮啮合损失对传动效率的影响

4.1 齿轮啮合损失计算结果

各变速器齿轮的主要几何参数见表1。

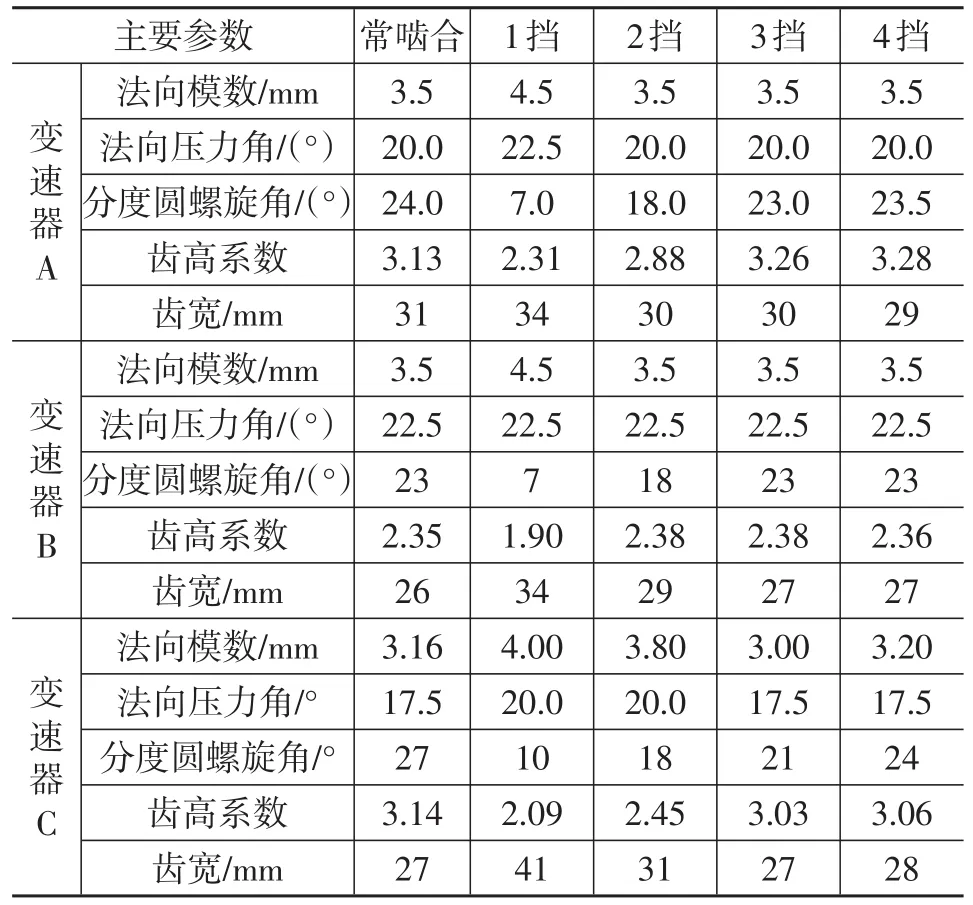
表1 各变速器齿轮的几何参数

在效率评价点处的单对齿轮啮合效率计算结果如图5所示。可知，变速器B的齿轮啮合效率最高，变速器C其次，变速器A各齿轮比变速器C低0.1%～0.16%，比变速器B低0.14%～0.24%。

图5 各变速器齿轮啮合效率计算结果

变速器A与变速器B除齿轮参数外，其余部分没有改变，两个变速器各挡位效率试验结果的差值主要是由齿轮啮合损失的差异造成的。各挡齿轮啮合效率计算结果的差值与试验结果的差值对比结果如图6所示。相对误差最大为14%。其中计算误差的主要来源一方面是由于计算模型中摩擦系数影响因素众多[8]，为了方便比较齿轮几何参数的影响，在模型中取为定值，另一方面是没有考虑加工精度及齿轮微观修型的影响[7,9]。

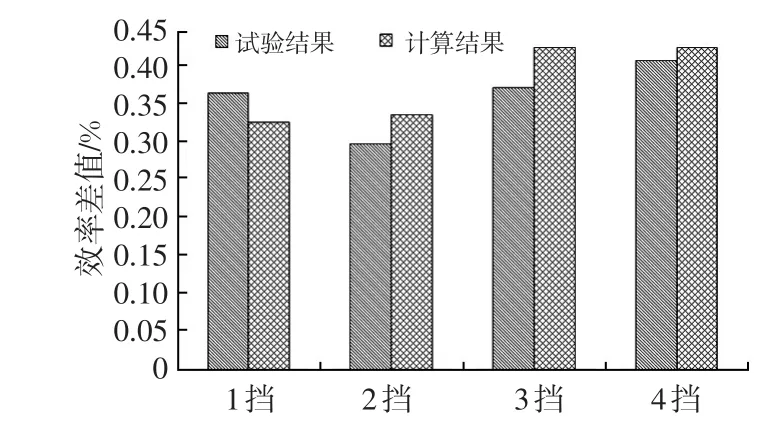
图6 变速器A与B效率试验与计算结果

4.2 齿轮参数对啮合损失的影响分析

为了说明齿轮各几何参数对啮合效率的影响，以变速器A中常啮合齿轮为例，以表1为基本参数，在保证中心距不变的前提下，通过在一定范围内改变影响因素的取值，分析齿轮参数对啮合效率的影响。计算结果见表2。

从表2可以看出：

a.压力角增大，导致基圆减小，啮合线长度减小，齿轮啮合的相对滑动速度减小，有助于提高斜齿轮的啮合效率，但端面重合度会降低；

b.适当减小螺旋角，有助于提高斜齿轮的啮合效率，但端面重合度和轴向重合度会降低；

c.减小全齿高，在基圆不变的前提下，可有效减小啮合线长度，有助于提高齿轮啮合效率，但端面重合度会降低；

d.减小模数，可有效提高斜齿轮啮合效率，但端面重合度会降低，轴向重合度会增大，且端面重合度降低的程度比轴向重合度增大的程度要大；

e.减小模数的同时，适当增大螺旋角，仍会提高斜齿轮啮合效率，且可增加轴向重合度。

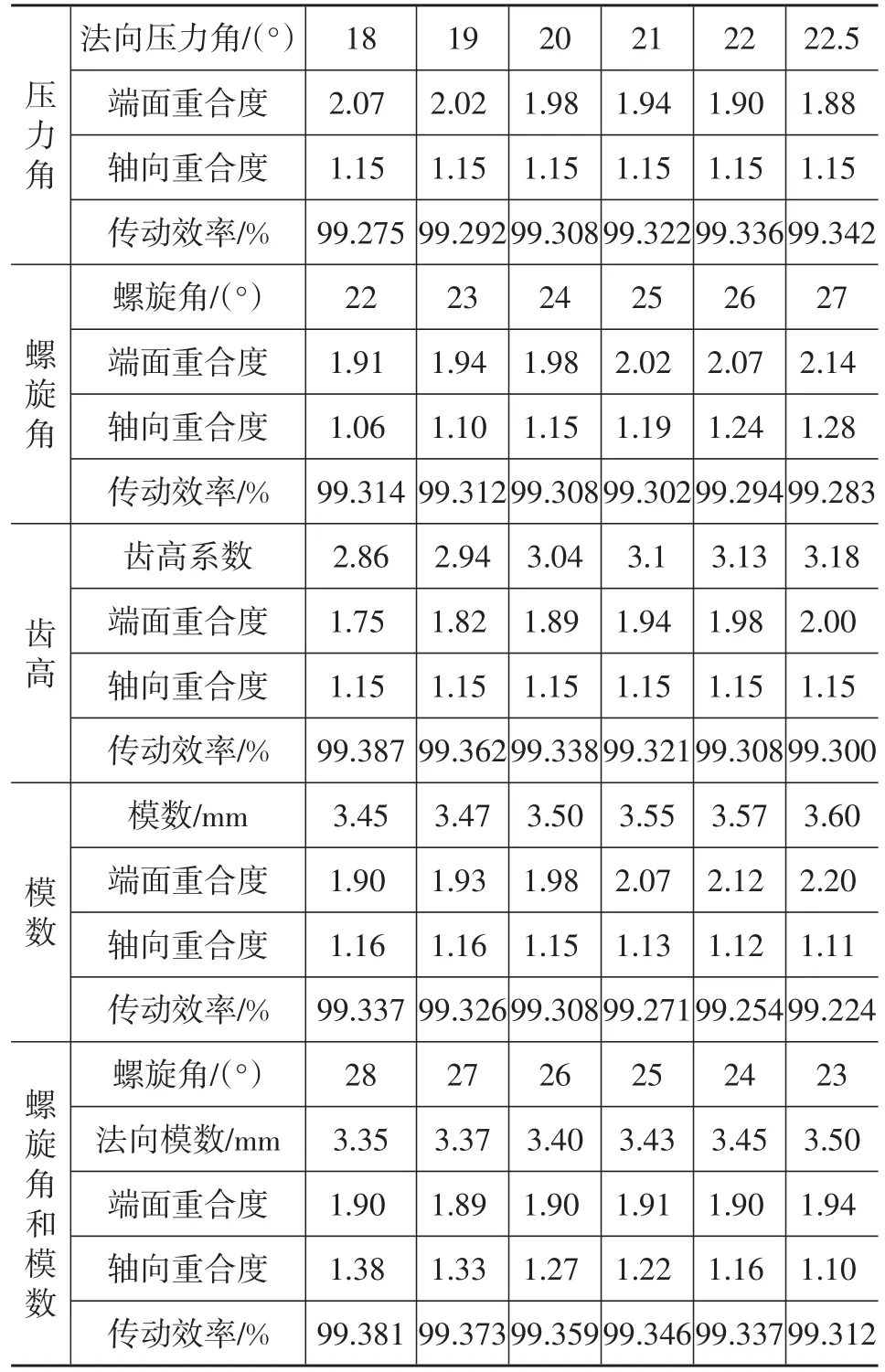
表2 齿轮参数对啮合效率的影响

由表2可知，变速器A与变速器B相比，在其它参数基本不变的前提下，单纯通过增加齿高，从而增加端面重合度的方式来改善NVH性能会导致齿轮效率的降低。而从图7变速器A和变速器C重合度对比可以看出，除2挡齿轮外，变速器C的重合度与变速器A基本相当，但其效率仍比变速器A高。因此，在提高变速器重合度的同时，需要对齿轮参数进行优化以提高其效率性能。

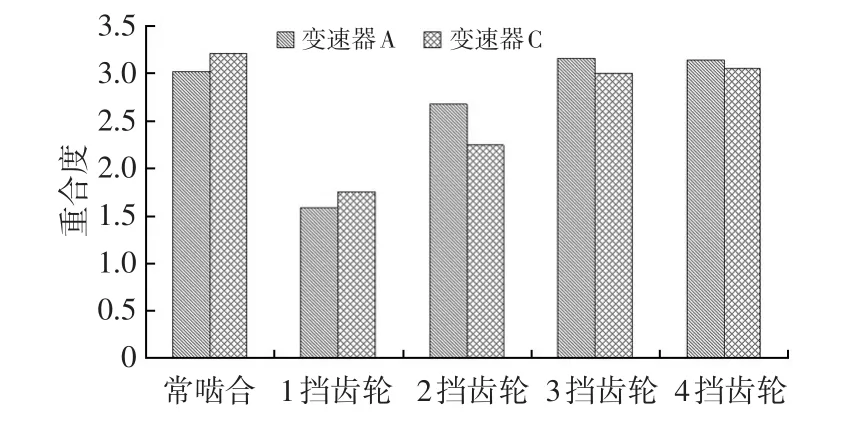
图7 变速器A和变速器C重合度对比

5 轴承摩擦损失对传动效率的影响

5.1 轴承摩擦损失计算结果

各变速器轴承的基本参数见表3。在效率评价点处变速器A和变速器C的轴承效率计算结果如图8所示。可知，变速器A的轴承效率比变速器C的低0.14%～0.37%。

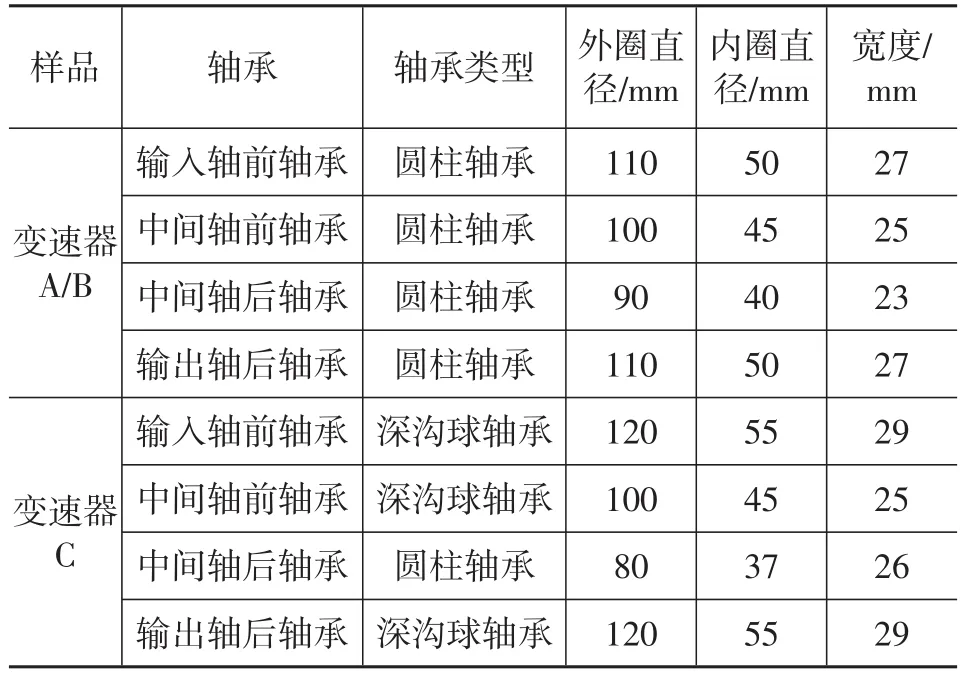
表3 轴承的基本参数

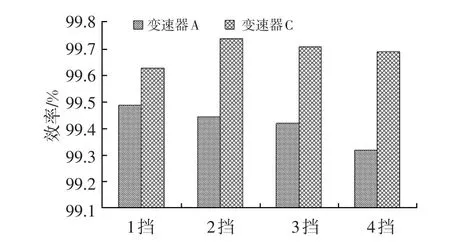
图8 变速器A与变速器C的轴承效率计算结果

考虑齿轮啮合损失与轴承损失的共同影响，变速器A与变速器C各挡效率计算结果的差值与试验结果的差值对比如图9所示。相对误差最大为22%。计算误差的主要来源一方面是由于计算模型没有考虑无负荷损失的影响，另一方面除齿轮的因素外，轴承的加工精度及摩擦系数的取值对结果均有一定程度的影响。

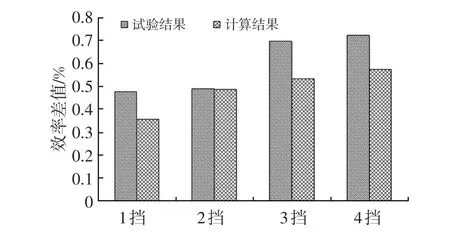
图9 变速器A与C各挡效率试验结果差值与计算结果差值

5.2 轴承选型对摩擦损失的影响分析

根据各轴承摩擦损失的计算结果，将变速器各位置的轴承效率损失进行分解，见表4。由表4可知，变速器A输入轴前轴承单位功率损失比对标变速器C的要大1倍以上；随着挡位的增加，变速器A输出轴后轴承的单位功率损失有大幅增加。输入轴前轴承比输出轴后轴承功率损失大的原因是输入轴转速比输出轴高很多，随着挡位的增加，输出轴转速升高，所以损失也随之增大。

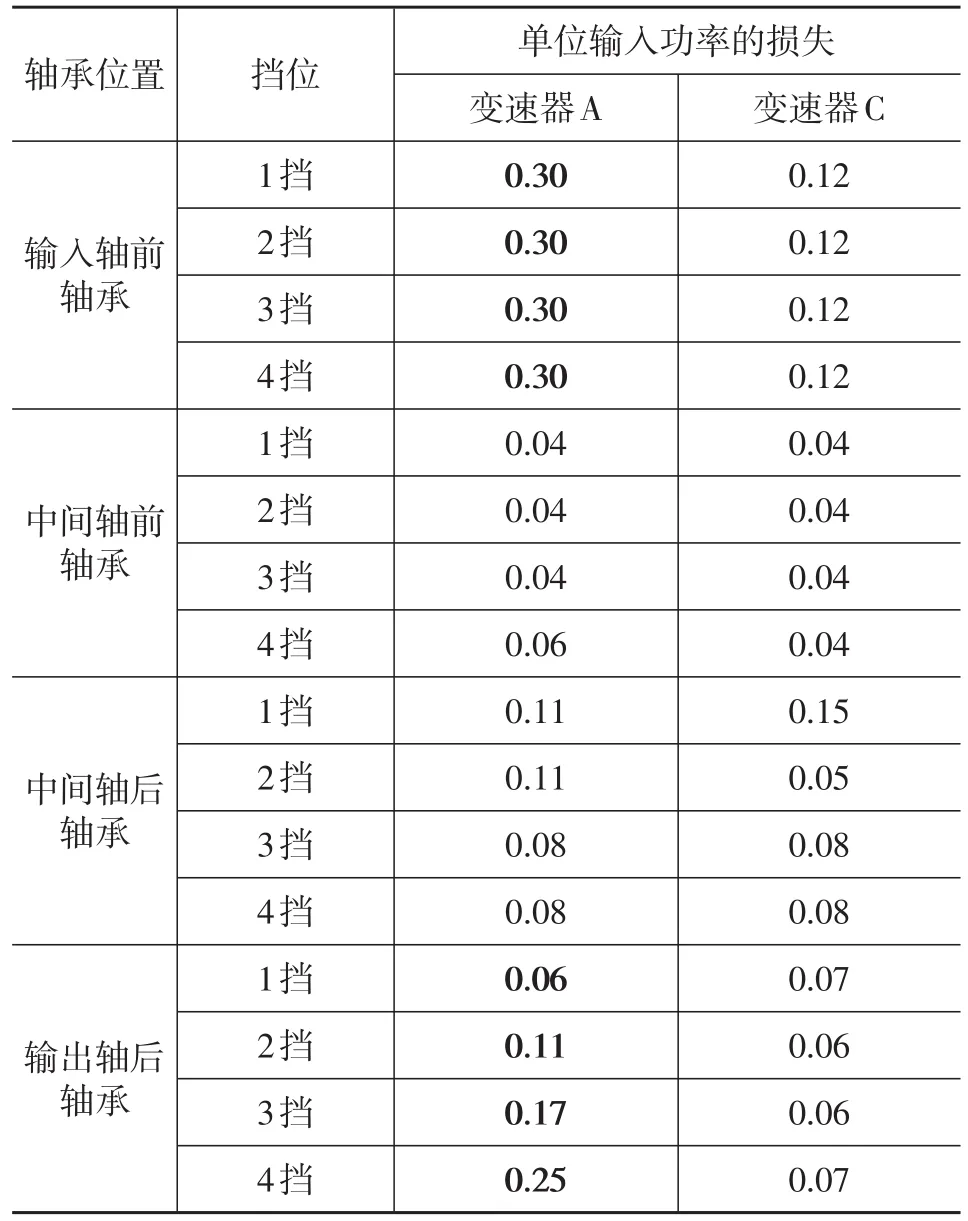
表4 变速器各位置处轴承效率损失分解 %

变速器A和变速器B的输入轴前轴承和输出轴后轴承均采用圆柱滚子轴承，而变速器C所采用的均为深沟球轴承。由式（7）和式（8）可知，圆柱滚子轴承需要单独考虑轴向载荷引起的附加摩擦损失M2，而承受轴向力时，圆柱滚子端面的滑动摩擦系数f2比径向载荷所导致的滚动体摩擦系数f1大4倍以上[6]。因此，可以判断轴承型式选用不当也是导致变速器A效率偏低的原因之一。

6 效率提升方案及试验验证

6.1 齿轮参数优化

6.1.1 设计变量

在保证变速器重合度和耐久性的前提下，对影响效率的主要设计参数法向模数mn，分度圆螺旋角β，法向压力角αn，齿高系数ha1、ha2，齿数z1、z2进行优化，以最大程度提高效率。

6.1.2 约束条件

6.1.2.1 几何约束条件

a.变速器中心距保持不变，通过齿轮无侧隙啮合的条件进行保证：

式中，ebt2为从动齿轮基圆端面齿槽宽；sbt1为主动齿轮基圆端面齿厚；db1和db2为主、从动齿轮基圆直径。

b.齿轮速比变化不超过原速比u21′的±1%：

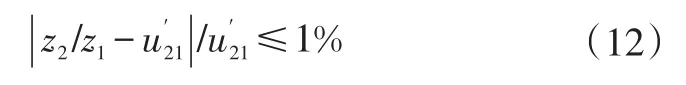
式中，z1和z2为主、从动齿轮齿数。

c.齿轮重合度不低于原设计重合度εΣ′要求：

其中，

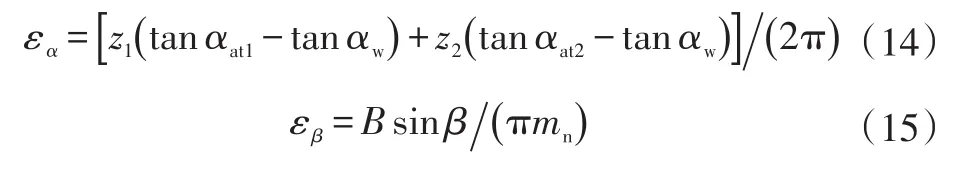
式中，αat1和αat2为齿顶圆端面压力角；B为齿宽；β为分度圆螺旋角；mn为法向模数。

d.啮合时齿顶不干涉，即齿轮啮合起始点的直径dSAP要大于或等于渐开线起始点的直径dFf，其渐开线起始点为渐开线与齿根过渡曲线的交点。

e.为保证变速器的总长度不变，故约束齿宽保持不变。

6.1.2.2 强度及耐久性约束条件

a.齿轮齿顶法向厚度San要大于0.3mn：

式中，xt为变位系数；αt为分度圆端面压力角；αat为齿顶圆端面压力角；z为齿数；mn为端面模数；βa为齿顶圆螺旋角。

b.齿轮弯曲和接触疲劳安全系数要不小于变速器B齿轮的要求，可根据文献[10]计算。

6.1.2.3 设计变量的边界约束条件

根据设计经验，1挡法向模数为4≤mn≤5，其余挡位的法向模数为3≤mn≤4；法向压力角为18≤αn≤25；常啮合齿轮分度圆螺旋角为22°≤β≤26°，1挡齿轮取为6°≤β≤8°，2挡齿轮为17°≤β≤19°，3、4挡齿轮为21°≤β≤25°；齿高系数ha为初始值±1。

6.1.3 优化方法及结果

采用遗传算法GA进行方程求解。设计变量的优化结果见表5。各单对齿轮优化后的效率如图10所示，较优化前提高0.1%～0.2%。

6.2 轴承类型的改进方案

将变速器A的输入轴前轴承及输出轴后轴承的轴承型式由圆柱滚子轴承更改为深沟球轴承，重新进行轴承效率计算，改进前后的效率对比结果见表6。

表5 设计变量优化结果

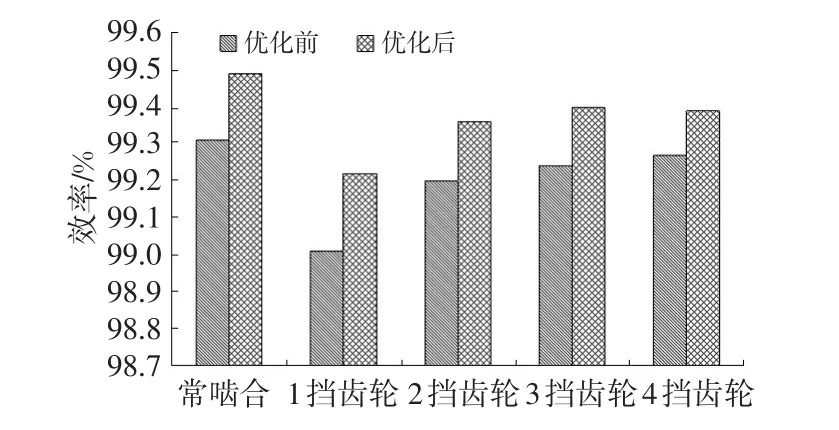
图10 效率优化结果

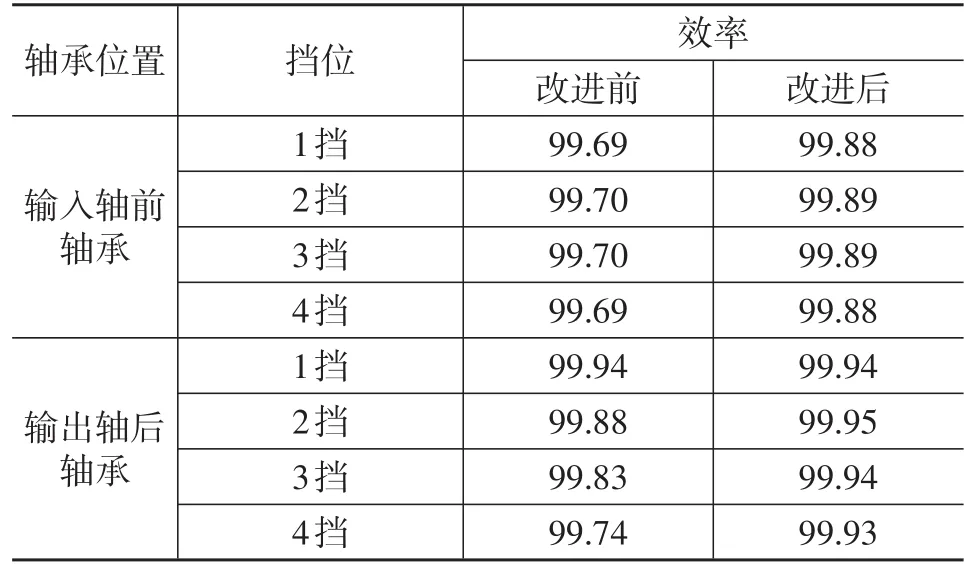
表6 改进前后的轴承效率对比%

由表6可知，改进后各挡工况下，输入轴前轴承效率提高0.19%；输出轴后轴承效率提高0.07%～0.19%。

6.3 试验验证

对改进后的变速器A重新进行效率试验，结果如图11所示。可知，变速器A的效率较改进前提高了0.55%～0.70%，达到与变速器C相当的水平。其中改进后齿轮和轴承对效率提高的贡献度见表7。

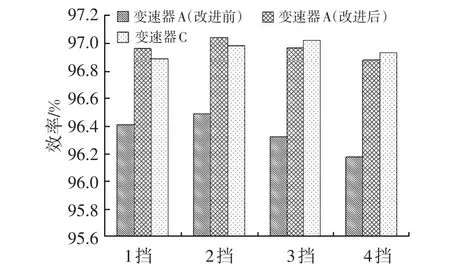
图11 改进后变速器A效率试验结果

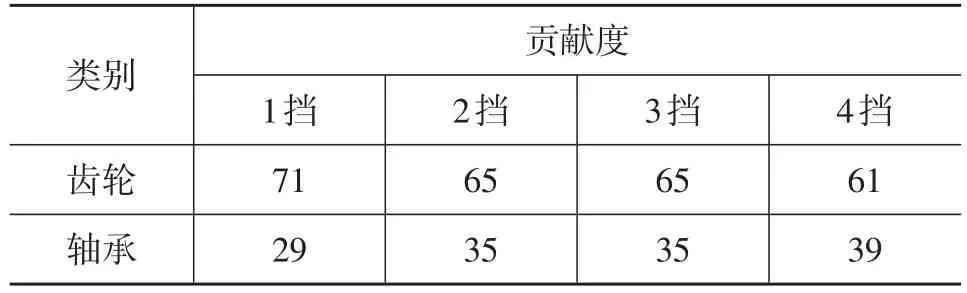
表7 改进后轴承和齿轮对效率提高的贡献度 %

7 结束语

a.以某变速器传动效率偏低问题为例，通过与对标样箱效率试验数据的对比分析，确定了与载荷相关的损失偏大是导致该变速器效率偏低的主要因素；

b.建立了齿轮和轴承功率损失的数学模型，分别对齿轮及轴承的效率进行了理论计算，分析了齿轮的主要设计参数对传动效率的影响。通过单纯增加齿高来提高齿轮的重合度，以及轴承选型不当是导致该变速器效率偏低的原因；

c.在保证齿轮耐久性以及NVH性能的基础上，采用遗传算法的优化方法，以效率最大化为目标，重新对齿轮进行了优化设计，并更改了轴承类型。改进后的变速器经试验验证得，其传动效率提高了0.55%～0.70%，达到了对标变速器的效率水平。

1 王治平，章新.汽车变速器传动效率的建模与仿真.汽车工程，2014(10)：1285～1288.

2 王熙，秦大同，胡明辉，等.汽车变速器传动效率理论建模与试验测试.机械传动，2010,42(8)：21～24.

3 SAE J2453-1999：Manual Transmission and Transaxle Effi⁃ciency and Parasitic Loss Measurement.1999.

4 张慧芳，张立荣.手动变速器传动效率的影响因素分析与改善对策研究.制造业自动化，2011(2)：31～33.

5 QC/T 29063-2011：汽车机械式变速器总成技术条件.北京：中国标准出版社，2011.

6 AGMA/ISO 14179-1-2001：Gear Reducers-Thermal Ca⁃pacity Based on ISO/TR 14179-1.2001.

7 王成，方宗德，贾海涛.斜齿轮滑动摩擦功率损失的计算.燕山大学学报，2009,33(2)：99～102.

8 王斌，陈辛波.混合润滑状态下渐开线直齿轮啮合效率分析.同济大学学报(自然科学版)，2014,42(12)：1904～1910.

9 王涛，李宏玲.齿轮精度对变速器传动效率的影响研究.客车技术与研究，2015(5)：56～59.

10 ISO 6336：Calculation of Load Capacity of Spur And Heli⁃cal Gears.2008.

（责任编辑 晨 曦）

修改稿收到日期为2016年10月13日。

Cause Analysis and Improvement on Low Efficiency of A Commercial Vehicle Transmission

Chen Dexin,Chen Xi,Sun Youqing,Yang Qi,Shi Xinglei
（China FAW Corporation Limited R&D Center,Changchun 130011）

In the product development,the problem of low transmission efficiency of a transmission was taken as example.By comparison with the test data of benchmarked transmission,the main factor that leads to the low efficiency of the transmission is bigger load-dependent loss.The mathematical model of gear and bearing power loss was established,the cause of low efficiency was analyzed in term of gear parameters and bearing selection.The parameters of the gear were optimized using genetic algorithm,and the bearing type was changed.The optimized test results showed that,transmission efficiency is increased by 0.55%～0.70%,meeting the transmission efficiency of the benchmarked transmission.

Transmission,Transmission efficiency,Optimum design

变速器 传动效率 优化设计

U463.2

A

1000-3703（2017）07-0010-06