视线系空间软交会常值推力控制方法设计
沈昱恒 张 迪 石 琛
上海机电工程研究所,上海 201109
视线系空间软交会常值推力控制方法设计
沈昱恒 张 迪 石 琛
上海机电工程研究所,上海 201109

研究了视线坐标系内的空间软交会常值推力控制方法。首先,描述了常值力约束下的空间软交会控制问题与交会运动模型,并将非线性视线动力学交会模型处理成一种由距离、径向速度和切向速度作为状态量的新型状态相关模型。然后,根据预测控制基本思想,提出了常值控制指令和开关机时间约束下的滚动优化控制方案,包括预测模型获取、滚动优化指标和控制流程。在指标设计中,通过在二次型优化指标函数中引入剩余飞行时间与切向速度构成的切向位移误差项,改善了控制效能。最后,通过多组数字仿真验证了对于圆轨道和椭圆轨道的自主接近任务本文设计的方法均有效适用。 关键词 预测控制;交会;常值力;视线
空间交会机动的形式有3种:软接触、硬接触和悬停(编队飞行)。进行软接触的交会(软交会)常用于大型航天器的组装、运输货物和替换乘员等,即通常所说的交会对接。同时软交会机动也可用于空间软攻击、俘获等军事任务[1]。由于软攻击不会带来空间碎片问题,所以是一种较为理想的攻击方式。但相较于硬攻击方式,软攻击任务需要对接近速度精确控制,显然这将使控制方式更复杂,控制方法的设计也更困难。
当前,按照控制量表现形式,近距离交会控制设计方法可分为2类:1)交会控制量为连续形式[2-4],即要求轨控发动机能够提供连续可变的推力,该类方法通常基于经典控制或现代控制理论,便于设计,但实现难度大;2)控制指令为常值约束形式,该类方法考虑实际工程约束,但控制设计难度较大。交会控制设计可将连续控制转化为开关工作形式[5-6]。文献[7]采用模糊/PID混合控制研究了自主交会最终逼近段的轨道控制问题。文献[8]基于线性T-H方程提出了轨道自主接近常值推力滑模制导和势函数制导方法。但是这2种方法的开关区域设计依赖于交会的起始条件,也就是对于不同的交会初始条件需要重复设计开关线,这样交会的自主性程度将有所下降。
利用常值推力实现控制律必然是分段非连续的控制律,依据经典控制方法难以实现。而预测控制是以计算机为实现手段,本身即是非连续的采样控制算法,随着计算机技术发展,预测控制在飞控领域[9-10]和导弹制导律设计领域[11-12]得到了许多应用。从这些研究可以看出,预测控制是处理对控制指令和状态有约束控制问题的非常有效的方法,利用预测控制中的滚动优化思想设计交会常值力控制方法具备可行性。
本文依据预测控制原理,研究控制指令常值约束和开关机时间受限状况下的在轨交会自主接近制导控制设计问题。依据一般交会运动模型,利用预测控制的基本思想,以发动机开关机时间为最小预测时间,以交会预测状态和当前控制输入的二次指标函数为设计指标,得出交会控制计算方法。根据实际自主接近过程划分控制指令集合,给出了具体的控制策略。最后,在非线性视线交会模型基础上给出具体的自主接近制导控制方案,并通过数值仿真分析了控制方案的效能。
1 问题描述及数学模型
1.1 常值推力软交会控制问题描述
空间交会相对运动模型可用以下一般形式表示:

(1)
式中,x(t)是对应交会状态量;g(x(t))为控制矩阵;u(t)为控制输入向量。
假设在常值推力约束条件下,不考虑主动航天器质量变化影响,可合理认为在轨道坐标系的各轴向存在幅值及特性均相同的控制指令。追踪航天器沿坐标系各轴向的控制指令与发动机推力有准确的对应关系。设各轴控制指令均有5个幅值,则控制量幅值域为Cu={-uh,-ul,0,uh,ul},其中,uh为较大常值控制指令,ul为较小常值控制指令。上述控制约束在工程上存在合理性,以“神舟”飞船的推进系统为例,共安装了4组额定真空推力为2500N的轨控发动机和8组150N的姿轨控发动机用于轨道机动控制。
另外,实际发动机开关机不可过于频繁,因此发动机存在最小工作时间间隔Tmin,即开机和关机的最小时间间隔均为Tmin。因此,t时刻的控制指令满足的集U(t)=c|c∈CU,t∈[t,t+ηTmin],t∈[t0,tf]其中,t0为交会起始时间,tf为终端时间,η为自然数。
常值推力交会控制问题可归纳为:对式(1)描述的空间交会运动,在期望交会停泊点距离ρd终端约束条件下,设控制量u(t)∈U(t),当交会时间从t=t0开始到达终点时刻tf时,满足终端距离条件和速度条件
ρ(tf)=ρd,V(tf)=0。
1.2 视线系交会运动模型
通常在自主交会段,追踪航天器与目标航天器的轨道倾角误差已消除,两航天器处于共轨道面,此时的视线系相对运动模型为
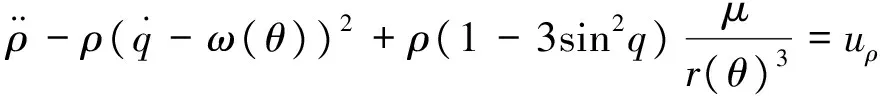
(2)
其中,ρ为距离,q为视线角,μ为地球引力常数。ω(θ)为目标器轨道角速度,r(θ)为目标器地心距,θ为目标器轨道真近点角。在偏心率轨道上,真近点角θ为时变量,因此,方程组(2)具有时变性、非线性和强耦合的特征。其中,第1式描述径向运动规律,第2式描述切向运动规律。
(3)


(4)
式中,


其中,




因此,本文将d(x)项视作控制干扰量,而不放在预测模型中予以考虑,但在仿真计算中d(x)项不可忽略。综上所述,可将A和B矩阵构成的状态空间模型作为预测模型,表达式如下

(5)
2 交会预测控制方法设计
在给定控制指令集合和最小开关机时间情况下,控制量大小是可知的,控制设计是对交会过程控制量进行分配的问题。为减少控制设计的复杂性,将交会过程从初始时刻t0开始按最小时间间隔Tmin进行划分
[t0,t0+Tmin],[t0+Tmin,t0+2Tmin],…,
[t0+kTmin,t0+(k+1)Tmin],[tf-Tmin,tf]。
根据预测控制理论,首先需要在已知的当前系统状态和控制输入预测有限时间后系统未来的状态,这需要依据预测模型。对于线性定常系统,系统状态运动规律可通过系统状态转移矩阵,由外部激励作用和系统当前状态得到未来某时刻系统的状态[13]。对于视线系的空间交会问题,相对运动模型具有非线性和时变性的特点,很难求解状态转移矩阵,在此情况下可考虑将交会系统模型离散化,作为系统预测模型,通过离散化预测模型得到系统未来时刻状态与当前状态以及控制输入的关系。离散化的方式很多,本文采用较为简便的一阶差分形式。
设Ts为采样时间,记t=kTs为k,则在第k个采样时刻系统状态和输入分别为x(k)和u(k)。在Ts足够小的情况下,x对时间的导数可近似表示为
(6)
结合式(5)可得到离散模型为

(7)

Uk=c|c∈CU,k∈[k0,k0+ηTmin/Ts],k0∈Z,η∈n,其中,Z为包含0的整数集合。
若k时刻状态误差x(k)为初始条件,则k+1时刻的交会状态可由式(7)预测计算得到。同时可知,∀j∈{0,1,…,Nstep},Nstep为计算步数,任意时刻交会状态可由下式计算:


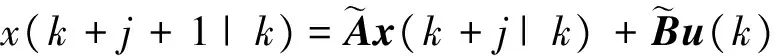
(8)
由于发动机存在最小工作时间Tmin约束,所以预测时间应满足T≥Tmin,为提高控制精度,可以选取T=Tmin,因此有Nstep=Tmin/Ts。设计中需要选取适当的采样时间Ts,保证Nstep为正整数。至此,系统状态预测表达式可表示为
x(k+Nstep|k)
(9)
为了使交会过程的能耗最小化,可选取当前时刻对应的优化指标为如下形式的二次型性能指标函数
J(k)=xT(k+Nstep|k)Qx(k+Nstep|k)+
uT(k)Ru(k)
(10)
其中,Q和R为待定正定对角矩阵。结合前文给出的视线系交会预测控制模型,对应的二次型性能指标函数设计如下
J(k)=
(11)
其中,α1>0,α2>0,β>0为待定的正常数;Tgo定义为剩余飞行时间,估算形式为
(12)
由于在视线运动模型中,只有径向距离量而不存在切向距离量,因此在指标函数中引入Vq(k+Nstep|k)·Tgo(k+Nstep|k)来表征切向位移误差量,与纵向距离量相对应,同时可以保证横向状态量Vq的快速收敛。指标函数式(11)中不妨令α2=1,这样指标函数仅依赖参数α1和β的大小。参数α1的大小主要影响交会过程的快慢,β则影响交会过程能耗。
对于给定的控制指令集合和初始状态误差,根据式(11)可得有限组J(k+Nstep|k)值,记所有J(k+Nstep|k)集合为Φ,即
Φ={J(u)|u∈Uk}
(13)
(14)
即
(15)
这样u*即为当前时刻的最优控制量。根据上述算法,可求得当前时刻到最小发动机工作时刻的发动机控制量。在整个有限时间的交会时间区间,重复上述过程可计算任意工作时刻应该提供的控制指令组合,这就是在常值控制指令约束下的滚动优化交会预测控制方法。
考虑到实际交会过程总是由远及近,误差一般在远距时大,近距时相应变小。为提高交会的远距快速性和近距的精度,并减少交会控制计算量,可以根据实际接近过程对算法进行改进,其主要思路为:根据距离信息来选择控制指令集合,远距时取大的控制量,近距时则仅取小控制量。控制指令集合可预先划分如下所示。
式中,L定义为控制切换边界距离。
3 数字仿真
仿真计算重点验证设计控制策略在椭圆轨道上自主接近的效能,同时以圆轨道交会情况作为比较。设目标航天器轨道半长轴a=7359.5km,椭圆轨道偏心率ecc=0.1,从真近点角(θ=0°)时刻开始交会控制。


表1 相对初始条件
追踪航天器各轴轨控指令集合由uh=±0.3m/s2和ul=±0.01m/s2两个等级构成。取控制切换边界参数L=100m,终端距离ρd=10m,离散化采样时间Ts=0.01s。发动机最小工作时间间隔为Tmin=3s。性能指标函数J中参数α1=5×10-5,α2=1,β=10。仿真结果见表2。
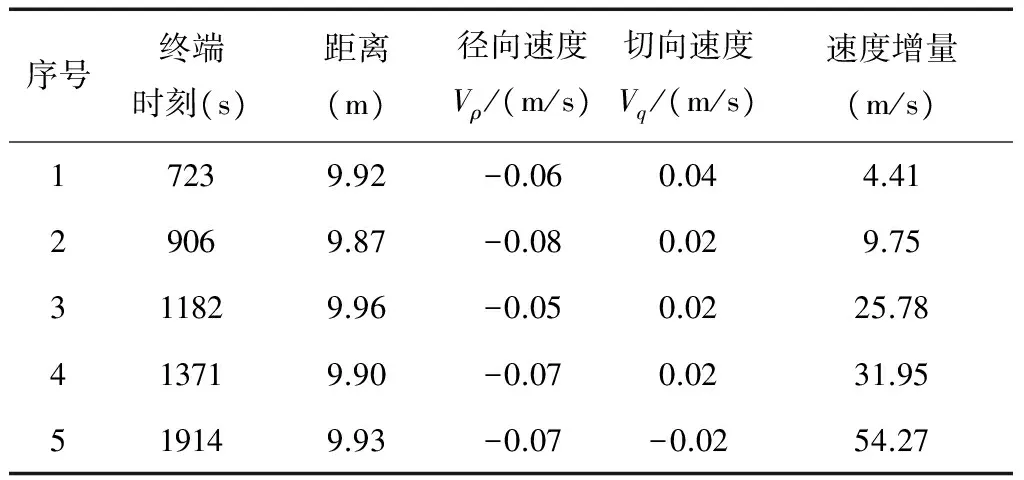
表2 仿真计算结果
从表2可知,终端位置精度很高,相对速度很小,满足软接触要求。多组初始条件说明该方法对初始条件不敏感。另外,所需速度增量与初始条件相关,但总体上较小。条件4的仿真曲线如图1~6所示。
由图1可知距离呈过阻尼形式单调收敛,不存在超调,收敛时间短,情况较为理想。图2和3分别给出了径向和切向速度收敛过程。图4为轨道坐标系中的自主接近轨迹,轨迹几乎呈直线形式。图5和6分别为径向和切向的控制指令施加情况,在发动机最小开关机时间限制的情况下,各轴控制指令施加频率均较低。
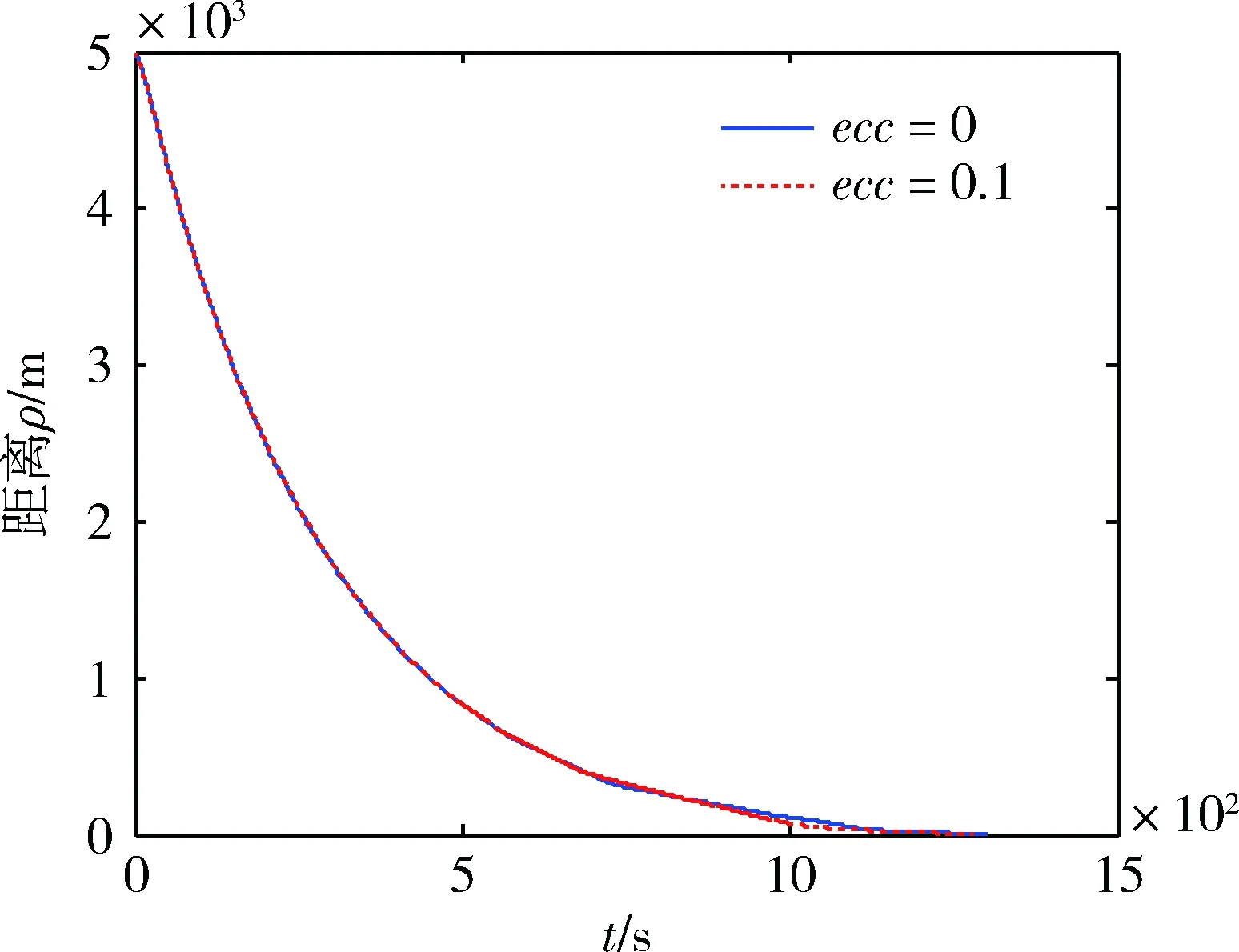
图1 距离

图2 径向速度

图3 切向速度
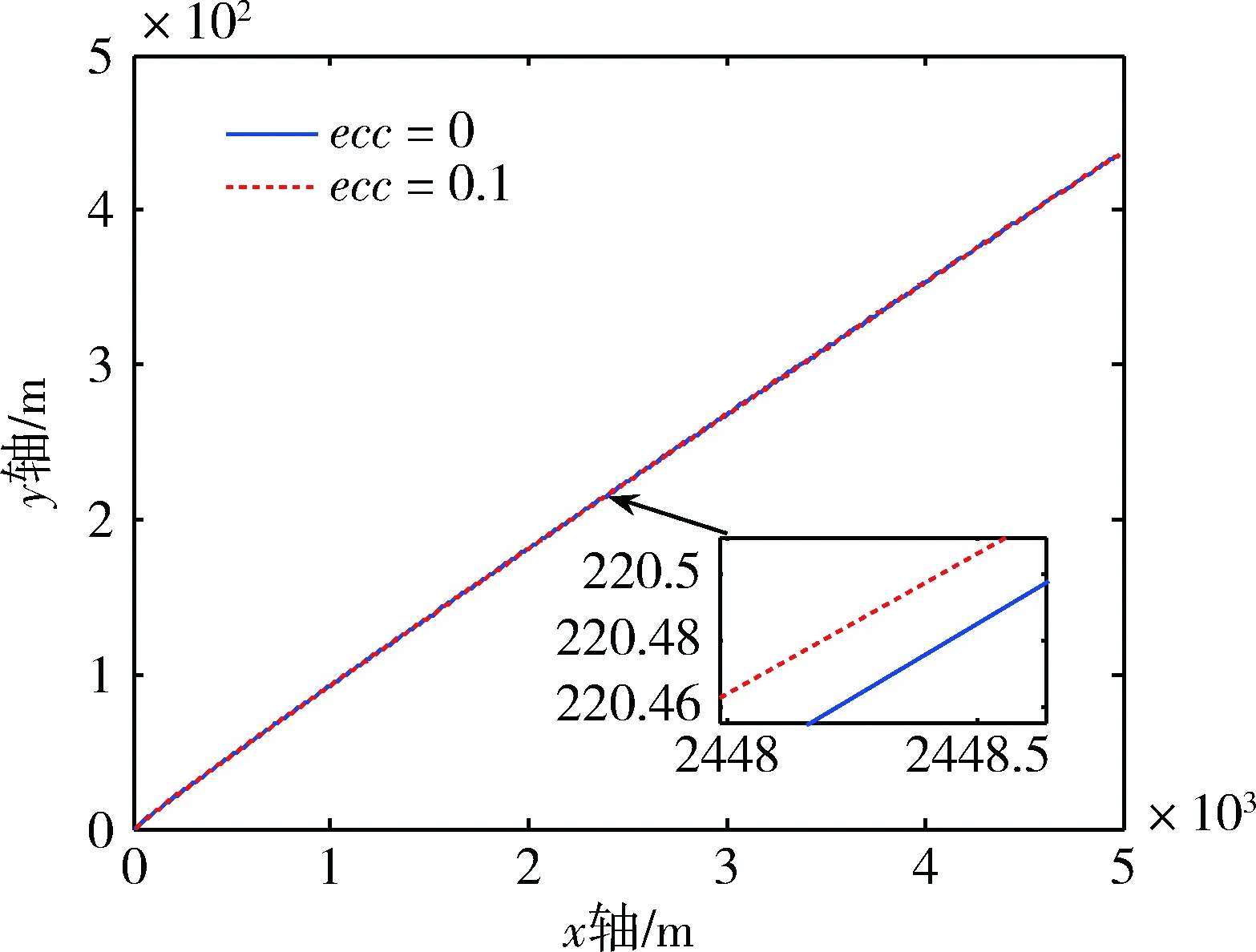
图4 交会相对运动轨迹

图5 径向控制指令
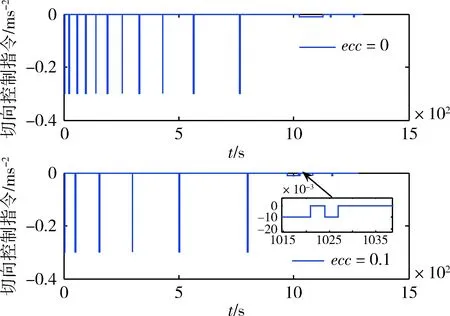
图6 切向控制指令
4 结论
根据实际的轨道机动轨控指令约束,包括可获得的常值形式控制指令约束集合和发动机最小开关机工作时间,设计了一种基于预测控制思想的常值指令在轨自主接近控制策略。文章最后通过多组数字仿真验证了控制方法的有效性和鲁棒性,同时对于圆轨道和椭圆轨道的自主接近任务,本文设计的方法均适用。
常值指令预测控制方法能够克服轨道未知信息量引起的干扰,鲁棒性强。特别是在只使用视线角速度信息和距离等较少测量信息的情况下,能够实现在轨自主软交会,这一优点对实施空间软攻击任务的交会具有重要价值。
[1] 吴蓓蓓,黄海. 空间多目标拦截交会平台停泊轨道设计优化[J]. 航天控制,2012,30(4):54-59.(Wu Beibei, Huang Hai. The Design and Optimization of the Parking Orbit of Space Multiple-targets Rendezvous or Interception Platform[J]. Aerospace Control, 2012,30(4):54-59.)
[2] 刘伟杰,谌颖. 航天器空间自主交会故障诊断与容错控制的集成设计[J]. 航天控制,2015,33(3):38-44,51. (Liu Weijie, Chen Ying. Integrated Design of Fault Diagnosis and Fault-Tolerant Control for Spacecraft Autonomous Rendezvous[J]. Aerospace Control, 2015,33(3):38-44,51.)
[3] 谭天乐. 椭圆轨道交会、悬停与绕飞的全状态反馈控制[J]. 宇航学报,2016,37(7):811-818. (Tan Tianle. Full State Feedback Control of Rendezvous,Hovering and Fly-around in Elliptical Orbit[J]. Journal of Astronautics,2016,37(7):811-818. )
[4] 张卓,张泽旭,谭浩. 基于鲁棒协同控制方法的多航天器交会问题[J]. 深空探测学报,2016,3(1):90-96. (Zhang Zhuo, Zhang Zexu, Tan Hao. Robust Coordination Control for Multi-Spacecraft Rendezvous Problems[J]. Journal of Deep Space Exploration, 2016,3(1):90-96.)
[5] Yao Y, Yang B Q, He F H, el al. Fliess Expansion Based Bang-bang Control Design and Its Application to Attitude Control of Missile[C]. The 6th, World Congress on Intelligent Control and Automation, Dalian, 2006: 188-192
[6] 荆武兴, 杨涤, 吴瑶华. 相对运动有限推力轨道控制[J]. 宇航学报,1993,(2): 35-41 . (Jing Wuxing, Yang Di, Wu Yaohua. Finite Thrust Orbital Control in Relative Motion[J]. Journal of Astronautics, 1993,(2): 35-41.)
[7] 李九人, 唐国金, 李海洋.自主交会逼近段的模糊/PID混合控制[J]. 宇航学报, 2010, 31 (3): 774-779. (Li Jiuren, Tang Guojin, Li Haiyang. Fuzzy/PID Hybrid Trajectory Control for Final Approach in Autonomous Rendezvous Mission. [J]. Journal of Astronautics, 2010, 31 (3): 774-779.)
[8] 陈统, 徐世杰. 椭圆轨道航天器自主接近的制导律研究[J]. 宇航学报,2008,29(6): 1786-1791. (Chen Tong, Xu Shijie. Research on Guidance Law of Autonomous Approach for Spacecraft Flying in Elliptical Orbits[J]. Journal of Astronautics, 2008,29(6): 1786-1791.)
[9] Richards A, How J P. Robust Variable Horizon Model Predictive Control for Vehicle Maneuvering[J]. International Journal of Robust and Nonlinear Control, 2006, 16: 333-351.
[10] Hegrenaes O, Gravdahl J T, Tondel P. Spacecraft Attitude Control Using Explicit Model Predictive Control[J]. Automatica, 2005, 41: 2107-2114.
[11] Dionne D, Michalska H, Rabbath C A. Predictive Guidance for Pursuit-evasion Engagements Involving Multiple Decoys[J]. Journal of Guidance, Control and Dynamics, 2007, 30(5): 1277- 1286.
[12] Singh L, Bortolami S, Page L A. Optimal Guidance and Thruster Control in Orbital Approach and Rendezvous for Docking Using Model Predictive Control[C]. AIAA Guidance, Navigation, and Control Conference. Toronto, Ontario Canada, 2010: AIAA 2010-7754.
[13] 葛志远, 侯明善, 沈昱恒. 固定推力空间自主交会控制[J]. 科学技术与工程, 2012, 12(8): 1825-1830.(Ge Zhiyuan, Hou Mingshan, Shen Yuheng. Autonomous Rendezvous Control under Fixed Thrusts[J]. Science Technology and Engineering, 2012,18(8):1825-1830.)
Constant Thrust Control for Space Rendezvous in Line-of-Sight Coordinate System
Shen Yuheng, Zhang Di, Shi Chen
Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109,China
Bystudyingtheconstantthrustusingsettingvalues(oneormore)canbeacquiredeasilyinengineeringrealization,apredictivecontrolapproachtospacerendezvousunderconstantthrustwiththeconstraintofengineminimumoperationtimeisdesignedinthispaper.Thediscreteline-of-sightpredictivemodelispresented,whichisbasedonnewstatespaceamountthatcontainsrange,rangerateandtangentialrate.Thenthepredictivecontrolstrategyisdiscusseddetailedly.Thequadraticoptimizationindexfunctionaboutthepredictedstatesandcontrolcommandwhichbelongtoafixedcommandsetisselected.Theoptimalcontrolcommandcanbeeasilydeterminedbyselectingtheminimumvalueofindexfunction.Thiscontroldeterminesthatprocesscanbeexecutedateverystepthatisfrominitialtimetotheend.ThispredictivecontrolstrategyisusedinLOSautonomousproximitysuccessfully.
Predictivecontrol;Rendezvous;Constantthrust;Line-of-sight
2016-11-02
沈昱恒(1983-),男, 江苏人,博士,工程师,主要从事战术导弹制导控制系统设计与研究;张 迪(1983-),男,安徽人,工程师,主要从事战术导弹制导控制总体设计;石 琛(1984-),男,江苏人,工程师,主要从事弹道及导引规律设计工作。
TP273.1
A
1006-3242(2017)02-0025-06

