探索数学规律 拓展思维深度

虞福平

数学家们认为“数学是思维的体操”，可以“培养智力使之敏锐”。然而，在我们的数学课堂经常会因为时间的顾虑而减少了思维的碰撞，学生的思维深度和广度得不到充分培养。其实，思维在于启发，在于生成，它留给学生的不是知识的结果，而是脑海里形成的过程。规律的探索就是激发思维的一种有效手段，它让学生从研究中思考，从结论中总结，变外在为本质，更加丰富生动地掌握知识。下面是我围绕书本的一道习题深入挖掘，拓展学生思维深度的教学案例：（苏教版六年级上册）

5.画一个长6厘米、宽4厘米的长方形。

（1）这个长方形的长和宽分别增加■后，各是多少厘米？先算一算，再画一画。

（2）现在长方形的面积是多少平方厘米？现在长方形的面积是原来的几分之几？

6.任意画一个长方形，再把长方形的长和宽分别增加■。先算出现在长方形的长和宽，再算出现在长方形的面积是原来的几分之几。

比较上面两题的计算结果，你有什么发现？

如果按照书上的习题的问法与要求，那学生在最多10分钟的时间内就能解决，但就这个规律的重点没有显现出来，学生在要求下步步到位，很难真正的内化并吸收，而且在规律得出后，没有体会优点的过程，学生很容易把它当成普通的知识，无法激起更多研究的热情。基于这样的认识，我进行了如下的拓展。

规律雏形：

我不仅要求学生找出现在的面积是原来面积的几分之几，为让学生把原理也弄清楚，我增加了下面几条要求：

现在的长是原来长的几分之几？

现在的宽是原来宽的几分之几？

现在的周长是原来周长的几分之几？

学生通过我的引导和自己举例推断发现：只要长方形的长和宽都增加■，那它现在的长是原来长的■，现在的宽是原来宽的■，现在的面积是原来面积的■，现在的周长是原来周长的■；周长与长和宽都是一样的，只要把原来的看做单位“1”，用1+■就可以得出，而面积正好是■的平方。

规律深入：

整体要求：四人一小组根据老师给的增加的分率，任意写一个长方形，像刚才那样研究，看看能不能找出面积、周长、长与宽变化对应的分率。

第一大组：长和宽都增加■，第二大组：长和宽都增加■，第三大组：长和宽都增加■。

【学生在进行讨论的过程中，我发现学生有上面的提示，规律都寻找得很正确，小组完成后，还在大组中讨论，更有学生发现了规律中的规律，显得异常的兴奋。】

结果汇报：

■

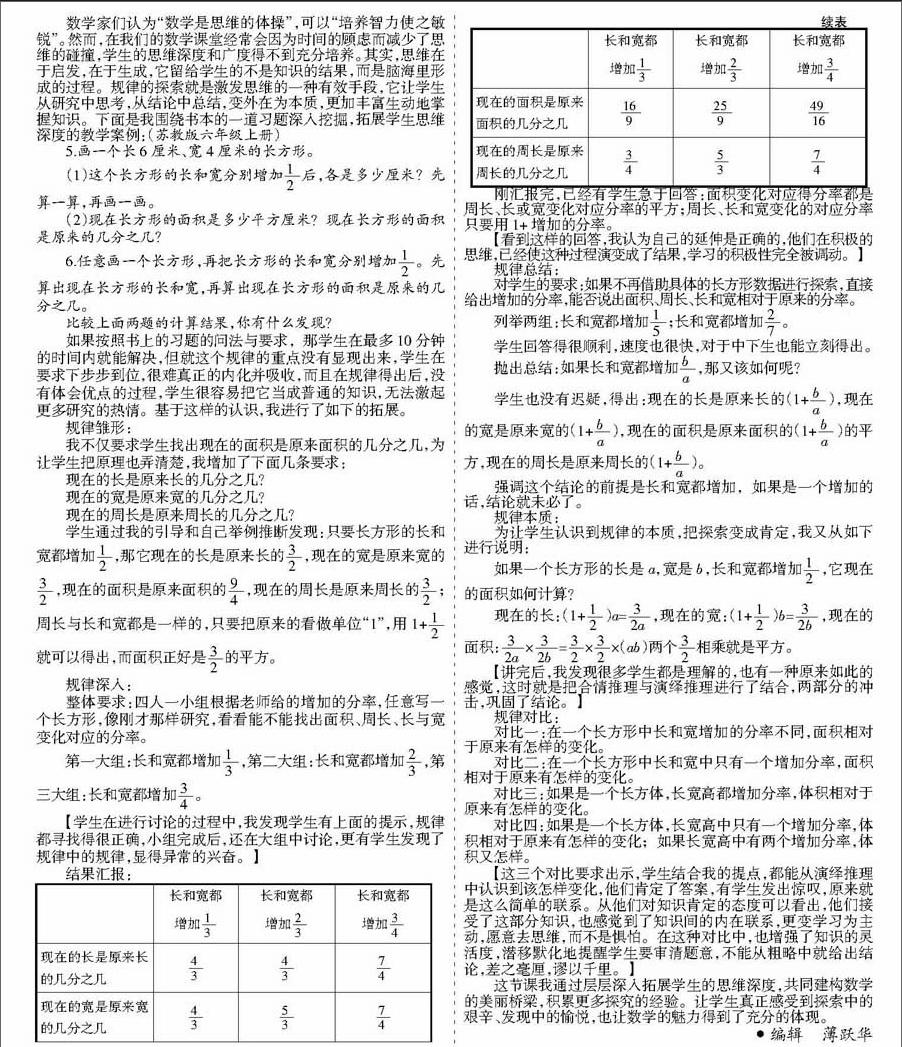
续表

■

刚汇报完，已经有学生急于回答：面积变化对应得分率都是周长、长或宽变化对应分率的平方；周长、长和宽变化的对应分率只要用1+增加的分率。

【看到这样的回答，我认为自己的延伸是正确的，他们在积极的思维，已经使这种过程演变成了结果，学习的积极性完全被调动。】

规律总结：

对学生的要求：如果不再借助具体的长方形数据进行探索，直接给出增加的分率，能否说出面积、周长、长和宽相对于原来的分率。

列举两组：长和宽都增加■；长和宽都增加■。

学生回答得很顺利，速度也很快，对于中下生也能立刻得出。

抛出总结：如果长和宽都增加■，那又该如何呢？

学生也没有迟疑，得出：现在的长是原来长的（1+■），现在的宽是原来宽的（1+■），现在的面积是原来面积的（1+■）的平方，現在的周长是原来周长的（1+■）。

强调这个结论的前提是长和宽都增加，如果是一个增加的话，结论就未必了。

规律本质：

为让学生认识到规律的本质，把探索变成肯定，我又从如下进行说明：

如果一个长方形的长是a，宽是b，长和宽都增加■，它现在的面积如何计算？

现在的长：（1+■）a=■，现在的宽：（1+■）b=■，现在的面积：■×■=■×■×（ab）两个■相乘就是平方。

【讲完后，我发现很多学生都是理解的，也有一种原来如此的感觉，这时就是把合情推理与演绎推理进行了结合，两部分的冲击，巩固了结论。】

规律对比：

对比一：在一个长方形中长和宽增加的分率不同，面积相对于原来有怎样的变化。

对比二：在一个长方形中长和宽中只有一个增加分率，面积相对于原来有怎样的变化。

对比三：如果是一个长方体，长宽高都增加分率，体积相对于原来有怎样的变化。

对比四：如果是一个长方体，长宽高中只有一个增加分率，体积相对于原来有怎样的变化；如果长宽高中有两个增加分率，体积又怎样。

【这三个对比要求出示，学生结合我的提点，都能从演绎推理中认识到该怎样变化，他们肯定了答案，有学生发出惊叹，原来就是这么简单的联系。从他们对知识肯定的态度可以看出，他们接受了这部分知识，也感觉到了知识间的内在联系，更变学习为主动，愿意去思维，而不是惧怕。在这种对比中，也增强了知识的灵活度，潜移默化地提醒学生要审清题意，不能从粗略中就给出结论，差之毫厘，谬以千里。】

这节课我通过层层深入拓展学生的思维深度，共同建构数学的美丽桥梁，积累更多探究的经验。让学生真正感受到探索中的艰辛、发现中的愉悦，也让数学的魅力得到了充分的体现。