基于AHP和熵权法赋权的变电站选址研究

赵思雯， 叶 鹏，姚天昊，赵叙龙，何 淼

(沈阳工程学院 电力学院，辽宁 沈阳 110136)



基于AHP和熵权法赋权的变电站选址研究

赵思雯， 叶 鹏，姚天昊，赵叙龙，何 淼

(沈阳工程学院 电力学院，辽宁 沈阳 110136)

变电站选址作为电网规划的关键工作内容，直接影响电力系统的运行可靠性和供电质量。充分考虑新能源接入对电网规划的影响，提出了一种基于AHP和熵权法赋权的变电站选址方法。针对电源分布情况、电网结构、环境情况、电网架构等评价指标与电动汽车充电站负荷，新能源发电容量，电气化铁路等量化指标构建多层次变电站选址评价体系模型，运用改进层次分析法和熵权法相结合的主客观并重的评价方法对变电站站址进行定量化研究分析，得到最佳变电站站址。以220 kV变电站选址规划工程为例，验证此方法的合理性和有效性。研究成果可为变电站选址提供技术参考。

变电站选址；层次分析法；熵权重；评价指标；结构模型

随着时代的发展，电力已然成为日常生活中不可缺少的一部分。我国的电力行业发展迅速，电网规模不断扩大，对变电站的规划、建设也提出了更高的要求，因此电力系统中变电站站址的选择具有重要意义。作为电网规划工作中的主要环节，变电站选址的科学合理性直接影响着供电的质量和运行的经济性。科学合理布局变电站不仅可以降低电能损耗，还可以节省建设投资。变电站的位置处于主网和配网的交汇点处，不仅是上级电网的负荷点，也是下级电网的电源处。变电站站址是电力系统规划合理性的关键点，不仅对电力行业的经济效益起着至关重要的作用，还影响着整个电力系统的结构。科学合理地安排变电站站址，对电网的经济可靠性、安全运行意义重大。

近年来，由于电力行业的重要性越发明显，而且变电站选址涉及的因素很多，因此在变电站选址方面学者们使用了不同的方法进行综合分析研究。文献[1]研究了单源和多源连续选址计算模型在不同原则下应用于变电站选址中,并构建了新的组合模型,致力于得出在一定负荷下变电站站址选择的最佳方案。文献[2]考虑到变电站选址中许多相关因素与地理空间信息有关,而且部分关键型指标不明确,文中运用了电网地理信息系统(GIS)的信息管理与空间分析功能,获得了不同备选站址的相关信息,并分析其实践可行性，使用模糊模式识别理论,综合分析并确定各选址决定性指标和目标数据的合理性。对于变电站选址来说，此方法大大地提高了综合决策准确度。文献[3]为了解决变电站选址的问题，使用智能启发式算法——遗传算法，这种算法分析容易、目的性强，然而，一旦问题规模增大，在进行简化处理的同时计算精度也随之降低。文献[4]采用模糊综合评判方法,通过对各因素的权重分配来确定其优先顺序，此结果对最终决策起着决定性作用。利用层次分析法来确定相关因素对于目标而言的权重，保证了最终结果的科学性，但是层次分析法又有其自身的缺陷,即判断矩阵的一致性与人们决策思维的一致性存在差异。

为了解决上述问题，针对电源分布情况、电网结构、环境情况、电网架构4个分析评价指标与电动汽车充电站负荷、新能源发电容量、电气化汽车铁路3种量化指标构建多层次变电站选址评价体系模型，运用改进层次分析法和熵权法相结合的主客观并重的评价方法对变电站站址进行定量化研究分析，将改进层次分析法计算出的相对权重与熵权重综合考虑，得到最佳变电站站址。此方法不仅考虑了客观性和主观性的统一，也避免了上述的一致性的问题。将改进层次分析法和熵权法综合应用在变电站选址中各因素指标权重的确定方面。

1 变电站选址相关因素

变电站选址是电网规划的主要组成部分，是进行电力系统建设规划的重要环节，因此进行变电站选址需严谨慎重，考虑全面。涉及到变电站选址的因素很多，不仅需要从经济角度考虑，也应该从技术条件上考虑。变电站选址应注意的因素：

1)负荷中心附近。选择变电站站址时，应考虑负荷相关因素在系统中的作用。在符合中心附近选址，可以达到降低电能损耗和减少电网投资的效果，还可以避免长距离输供电发生问题，提高电网安全可靠性。

2)合理布局电源位置。附近电源的建设情况直接影响着变电站站址的选择，尽量保证各电源与变电所不搭建在同一侧，不仅降低电网的投资，也能提高供电安全稳定性能。

3)确定进出线位置。各级电压线路位置的确定是变电站选址重要考虑因素之一，需保证电压线路的进出线位置不发生交叉跨越现象，尽量对终端塔建进行统一安置，走廊线路要进行集中放置。

4)合理选择站址区。选址过程中，要考虑节能减排、节约用地等因素。在规划时，要保证城乡的发展计划相协调；并尽量躲避常发生断层、滑坡地区；也应该考虑所选变电站与其他设备之间的相互影响，要有意避开有腐蚀性气体的工厂。

5)考虑交通运输。保证交通运输畅通，可以在搭建变电站时方便运输大量施工材料和变电器。为了未来的运行和检修，要保证选址的地区交通十分便利。

6)环境情况。尽量拥有可靠水源，保证水源的供给。同时也要考虑附近的住宅区，确定保护措施，防止对环境造成污染。

7)电动汽车充电负荷。负荷的位置，大小等不确定因素使电动汽车的充电负荷具有较大的随机性。电动汽车充电设备的分布情况和功率大小是保证变电站站址选择合理的重要因素。尽量保证电动汽车充电装置在密度较大的区域，这可扩大变电站的备用容量。

上述原则和因素是在变电站布点时通用方法中所必须考虑的，然而，在规划中，需要更好的考虑远景负荷特性，考虑现代城市的电气化的发展，考虑能源结构的调整和新能源大规模接入对变电站布点的影响。

2 变电站选址的结构模型

对于比较复杂的问题，可以将问题分成几层相关联的结构并构造一个层次关系，对层次关系进行分析研究。该研究旨在通过将变电站选址因素进行层次和熵权法进行分析，根据变电站选址要素综合分析，搭建变电站选址结构模型。目标层为变电站选址，准则层根据变电站因素分析研究分为电源分布情况、环境情况、土地因素和电网架构等分析指标和电动汽车充电负荷，新能源发电容量和电动汽车充电站负荷等量化指标。根据上述对影响变电站选址的因素的层次分析及结构总结，评价体系结构和层次结构表示如图1和2所示。

图1 评价体系结构

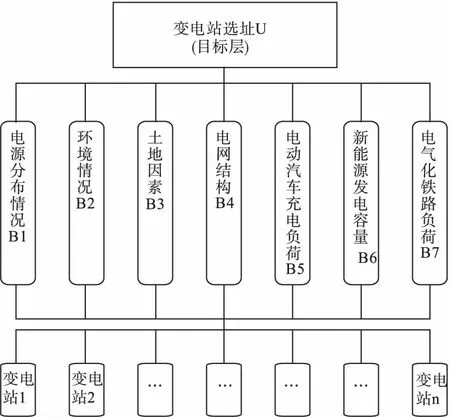
图2 变电站层次模型

3 评估方法

3.1 层次分析法

3.1.1 层次分析法的基本原理

层次分析法(AHP)是美国著名的运筹学家T.L.Saaty于1977年提出的一种定性和定量相结合的决策方法。该法的基本原理是将一个较复杂的问题分解为若干层次和若干因素,再根据两两因素之间的重要程度进行判断,并构建出判断矩阵,通过计算，将判断矩阵的最大特征值以及对应特征向量求出，求得的结果就是不同准则指标的权重,以此结果为依据，选择出最佳方案。早期的层次分析法有较大缺陷，不能保证结果的科学合理性,故该研究采用改进层次分析法，即在判断矩阵很难确定时,根据改进判断标度进行对比，从而构造最佳判断矩阵。

3.1.2 改进层次分析法权重系数确定方法

准则层对于目标层是以改进的层次分析法计算权重。总层目标对准则层指标进行两两比较，从而决定下层元素(准则层)对上层元素(目标层)的重要程度，即为相对权重。

第i个目标对第j个目标的相对权重记为aij≈ωi/ωj，n个准则层目标两两比较后得出的结果即为判断矩阵A：

(1)

式中，ωi，ωj分别表示目标i和目标j的相对权重，可使用Satty标度来反映比较目标之间的相对重要性，从而确定aij的值，如表1所示。

表1 目标相对重要性判断的Satty标度表

下层指标对于相邻上一层目标的相对权重是通过求解判断矩阵来实现的。通过求解矩阵A的最大特征值λmax及其特征向量P，将P进行归一化处理，得到权重向量，即：

对于判断矩阵A，如果判断者能够精确计算aij，则有：

(2)

在式(2)中，aij=aikakj称为一致性条件，如果具有一致性，则该判断矩阵一定是满足一致性的条件矩阵。根据正互反矩阵的重要性质，A的最大特征值应满足：λmax≥n(n为A的阶数)。

将判断矩阵的一致性进行检验，则需引入一致性指标CI(Consistence Index)。

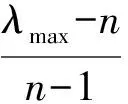
(3)

CI与表2中给出的随机性指标RI(RandomIndex)的数值之比称为一致性比率，即:

(4)

根据式(4)中CR值的计算结果，可以进行检验判断矩阵的一致性。如果CR<0.1，则满足一致性条件；若CR≥0.1，则不符合要求，此时应对所得判断矩阵重新进行计算估计。

3.2 熵权法

3.2.1 熵权法的基本原理

热力学中的熵是重要概念，在信息论方面，用来表述信息源发出信号状态不确定程度。在评价指标中获得的信息量直接影响着评价的精度与准确性。用熵权法所得到的上权重直接表述的是评价指标的相对重要性，评价指标的差异越多越说明重要，其权重也越高。在变电站选址过程中,熵权法所确定的权重，就是根据各评价指标之间的差异来确定权重。

表2 随机指标RI指标表

3.2.2 熵权确定方法

熵在不同领域有着不同的定义,可表示为:

(5)

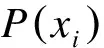
在评价模型中，如有m个目标，n个评价指标，则得到评价指标矩阵：

X=(xij)m×n

(6)

根据指标的差异程度，运用熵的概念，将各指标给定权重修正计算。其计算步骤为:

1)计算xij在指标j下的权重P(xij)

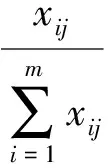
(7)

2)计算指标j的熵值ej

(8)

式中，k=1/lnm，当P(xij)=0时，令P(xij)lnP(xij)=0。

3)计算差异性因数gj

gj=1-ej

(9)

4)判断矩阵

定义了第j个指标的熵之后，第j个指标的熵权定义为：

(10)

根据以上分析可得，熵权法综合各指标提供的信息量并计算综合指标，得出评估问题时各指标在竞争意义上的相对激烈程度。作为一种客观的评价方法，是需要信息量的大小来确定权数值的。

4 辽宁典型电网实例计算

由图2可知，变电站选址评价指标体系是一个二级层次指标体系，在准则层中既有分析指标，也有量化指标。准则层中分析指标对目标层权重的确定采用AHP法，量化指标对目标层的权重确定采用熵权法赋权。方案层对准则层权重的确定采用AHP法赋权。以某市典型地区有量化指标和某地区无量化指标为例分别进行计算验证。

4.1 具有量化指标负荷中心附近变电站选址

在某地区中某负荷中心附近有5个变电站选址方案，即甲风电、乙变电站、丙线路交叉处、丁线路、戊变电站可供选择。因存在量化指标，则需要对分析指标和量化指标进行分别研究，且与专家研究分析得到指标相对重要性，从而进行负荷中心附近变电站方案选择。

4.1.1 准则层对目标层的权重分析

1)判断矩阵A

由专家对指标相对重要性进行两两比较，得判断矩阵 A

2)求解权重向量

将A的列向量进行归一化，计算 A的最大特征值及对应的特征向量，并将记为λmax和ζ。

λmax=7.429 7

ζ=(0.093 6，0.082 6，0.048 4，0.241 0，0.158 7，0.175 6，0.200 1)；

3)判断矩阵A是否具有一致性

计算CI，得CI=0.071 6；

查表得RI=1.32；

计算得CR=0.054 2<0.1，可知矩阵A具有一致性；

记各指标权重为ω

ω=ζ=(0.093 6，0.082 6，0.048 4，0.241 0，0.158 7，0.175 6，0.200 1)。

所以得知，B1、B2、B3、B4、B5、B6，对于目标层U的权重指数为0.093 6，0.082 6，0.048 4，0.241 0，0.158 7，0.175 6，0.200 1。

在该地区中需要考虑新能源发电容量，其指标为量化指标，则选用熵权法进行计算。

表3 新能源发电容量数据表

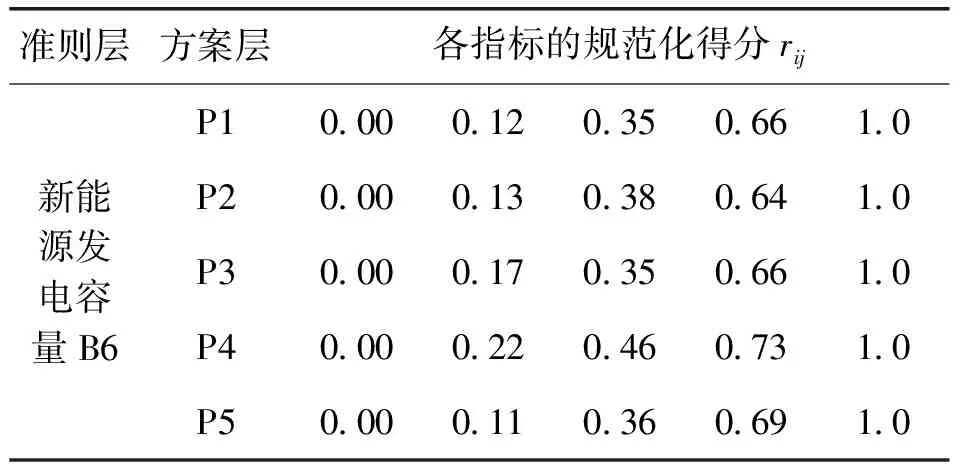
表4 各指标的规范化得分和熵权ωj

表5 各指标的规范化熵权ωj

因此，能源发电容量：

B6=0.121 5+0.099 7+0.077 0+0.161+0.127 3 =0.586 8

4.1.2 方案层对准则层的权重分析

对5个备选地址的分析指标和量化指标进行两两比较。这个过程与建立准则层对目标层判断矩阵步骤相同。需构建每个考虑因素的判断矩阵，并计算权重与检验一致性。对于4个分析指标来说，需获得每个指标的判断矩阵，4个判断矩阵和相对权重如表6～表10所示。

表6 P—B1的判断矩阵

表7 P-B2的判断矩阵

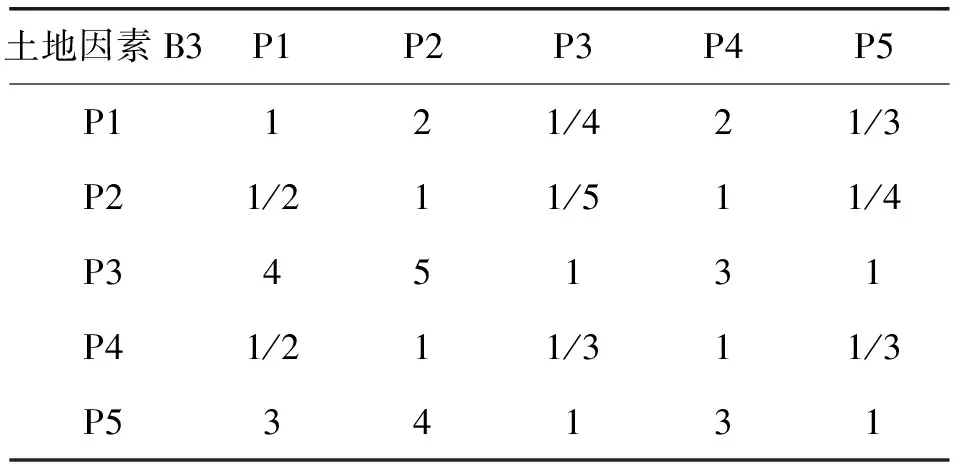
表8 P—B3的判断矩阵

表9 P-B4的判断矩阵

表10 相对权重表

判断矩阵的一致性比率分别为CRBi=(0.08，0.05，0.03，0.08)，可以看出，式中数值均小于0.1，故满足一致性要求。

4.1.3 层次总排序

根据以上层次单排序结果可以进行计算方案层中各评价指标对目标层的组合权重，并根据数据得出重要性排序，确定最佳方案。

方案层P相对于目标层U的权重向量：

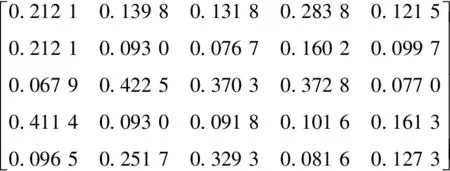
从上式得出的结论可知，方案丙的变电站位置更佳，既靠近负荷中心，又能分担附近变电站所承担的负荷。所以，方案丙为最佳地点。

4.2 无量化指标负荷中心附近变电站选址

某负荷中心附近有四个变电站选址方案，即A变电站、B变电站、C变电站、D变电站可供选择。与专家研究分析得到指标相对重要性，进行负荷中心附近变电站方案选择。

4.2.1 准则层对目标层的权重分析

准则层对目标层的权重计算步骤如下：

1)判断矩阵A

由专家对指标相对重要性进行两两比较，得判断矩阵A

2)求解权重向量

将A的列向量进行归一化，求得矩阵 A的最大特征值及特征向量，并将记为λmax和ζ

λmax=7.429 7

ζ=(0.093 6，0.082 6，0.048 4，0.241 0，0.158 7，0.175 6，0.200 1)；

3)判断矩阵A是否具有一致性

计算CI，得 CI=0.071 6；

查表得 RI=1.32；

计算得 CR=0.054 2<0.1，可知矩阵A具有一致性；

记各指标权重为ω

ω=ζ=(0.093 6，0.082 6，0.048 4，0.241 0，0.158 7，0.175 6，0.200 1)；

所以得知，B1、B2、B3、B4、B5、B6，对于目标层U的权重指数为0.093 6，0.082 6，0.048 4，0.241 0，0.158 7，0.175 6，0.200 1。

对4个备选地址的分析指标和量化指标进行两两比较。这个过程与建立准则层对目标层判断矩阵步骤相同。需构建每个考虑因素的判断矩阵，并计算权重与检验一致性。对于4个分析指标来说，需获得每个指标的判断矩阵，4个判断矩阵和相对权重如表11-表15所示。

表11 P-B1的判断矩阵

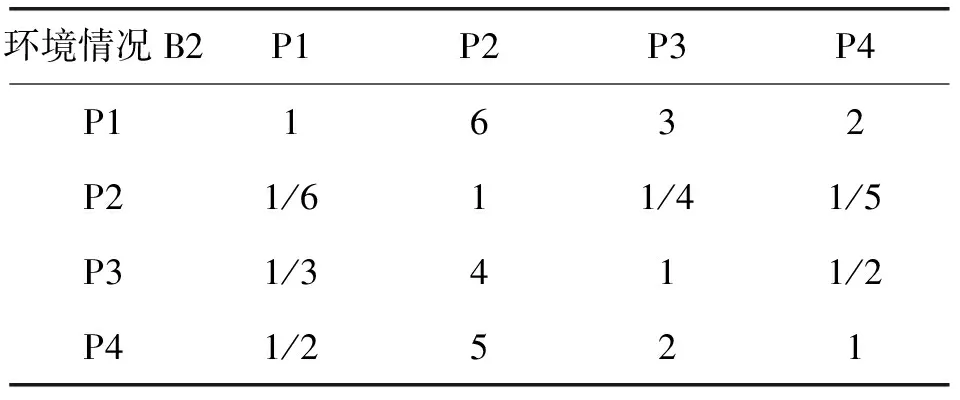
表12 P-B2的判断矩阵

表13 P-B3的判断矩阵

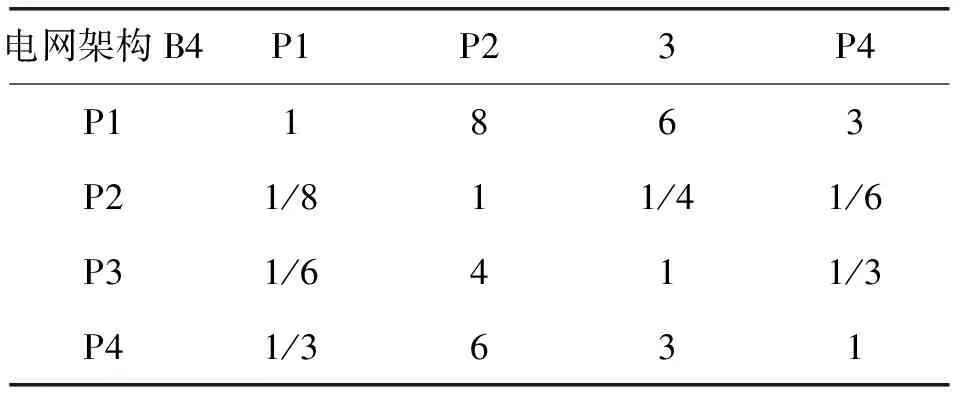
表14 P-B4的判断矩阵

表15 相对权重表

判断矩阵的一致性比率分别为CRBi=(0.08，0.03，0.07，0.07)，可以看出，式中数值均小于0.1，故满足一致性要求。

4.2.2 层次总排序

进行最后一步，层次总排序，方案层P相对于目标层U的权重向量：

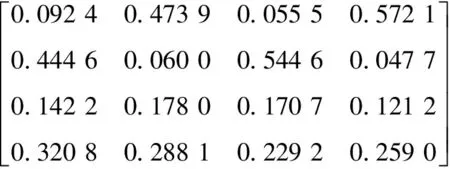
根据上式可得出变电站中电网架构相对措施层中其他指标更加重要。而方案A中的电网架构也更为合理，所以证实方案A是变电站选址的最佳方案。

5 结 论

变电站选址的科学合理性直接影响着电力系统的网络结构、供电质量和运行经济性。因此,选择合适的变电站站址是电网规划的重中之重。针对电源分布情况、电网结构、环境情况、电网架构4个分析评价指标与电动汽车充电站负荷、新能源发电容量、电气化汽车铁路3种量化指标构建多层次变电站选址评价体系模型，运用改进层次分析法和熵权法相结合的主客观并重的评价方法对变电站站址进行定量化研究分析，将层次分析法计算出的相对权重与熵权重综合考虑，得到最佳变电站站址。以220 kV变电站选址规划工程为例，验证此方法的合理性和有效性。研究成果可为变电站选址提供技术参考。

[1]周 敏,程浩忠,周中明.优化理论在城市配电网变电站选址中的应用[J].供用电,2003,20(2):7-10.

[2]杨丽徙,王家耀,贾德峰，等.GIS与模糊模式识别理论在变电站选址中的应用[J].电力系统自动化,2003,27(18):87-89.

[3]李鑫滨，朱庆军.变电站选址定容新模型及其遗传算法优化[J].电力系统及其自动化学报，2009，21(3)：32-35.

[4]贾德峰,许轶珊,任 群.用模糊综合评判法评价变电所所址[J].河南科学,2003,21(3):2-3.

[5]徐 青，吴 捷.模糊综合评判在变电站选址中的应用[J].电力建设，2004，25(7)：1-3.

[6]闫丽梅，许爱华，任 爽.一种变电站选址的新方法[J].高电压技术,2007,33(9)：75-77.

[7]李朝阳.农网变电所所址的合理选择[J].农村电气化，2001，3：1-2.

[8]B.A.Carreras,V.E.Lynch,I.Dobson，et al.Critical points and transitions in an electric power transmission model for cascading[J].Chaos,2002，12(4):985.

[9]B.A.Carreras,V.E.Lynch,D.E.Newman，et al.Blackout mitigation assessment in power transmission system[C]//Proceedings of the 36th Annual Hawaii International Conference on System Sciences,January 2003，Maui，Hawaii,USA.Washington，DC，USA：IEEE Computer Society，2003，2：65-74.

[10]张玉晰，王永滋，谭魁悌.变电所所址选择与总布置[M].北京：水利电力出版社，1986.

[11]Tanion T.Frizzy preference orderings in group decision making[J].Fuzzy sets and Systems,1984,12 (12):117-130.

[12]T.L.Saaty.层次分析法—在资源分配、管理和冲突分析中的应用[M].许树柏等译.北京:煤炭工业出版社,1988.

[13]王莲芬,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990.

[14]陈宜生,刘书声.谈谈熵[M].长沙：湖南出版社,1993.

[15]郭显光.一种新的综合评价方法—组合评价方法[J].统计研究，1995,5：56-59.

[16]周 晔.浅谈变电站的选址要素[J].云南电力技术,2009,5:69-74.

[17]齐文斌,南志远.综合评判模型在变电站选址中的应用[J].现代电力,1999,1:41-48.

[18]韦 钢,贺 静.电网规划中不确定性信息处理的现状及存在问题[J].上海电力学院学报,2003,4:33-37.

[29]费智聪.熵权—层次分析法与灰色—层次分析法研究[D].天津：天津大学,2009.

[20]何 淼,叶 鹏.基于多维度的城市饱和负荷预测方法研究[J].沈阳工程学院学报:自然科学版,2017,13(2):164-168.

(责任编辑魏静敏校对张凯)

SubstationLocationBasedonAHPandEntropyWeightMethod

ZHAO Si-wen,YE Peng,YAO Tian-hao,ZHAO Xu-long,HE Miao

(School of Electric Power Engineering,Shenyang Institute of Engineering,Shenyang 110136,Liaoning Province)

The substation location directly affects the operation reliability and power quality of the power system as a critical step in the power grid planning.A substation location method based on AHP and Entropy weight was proposed considering the impact of new energy access on grid planning fully.A multi-level substation site selection evaluation system model was constructed taking into account the valuation indexes such as the power sources distribution,power grid structure,environment,and power grid architecture,the electric vehicle charging station load,new energy generating capacity and electric railways.The optimal substation site was obtained on the basis of the quantitative analysis with the improved analytic hierarchy process(AHP)method combined with the entropy weight method.The rationality and validity of this method were verified by taking a 220kV substation planning project as an example.The conclusions of this paper can provide technical reference for other substations location.

Substation location; Analytic hierarchy process; Entropy weight; Evaluation index; Structural model

2017-05-22

赵思雯(1994-)，女，辽宁沈阳人，硕士研究生。

叶 鹏(1974-)，男，吉林吉林人，教授，博士，硕士生导师，主要从事电力系统运行与控制方面的研究。

10.13888/j.cnki.jsie(ns).2017.03.010

TM63

： A

： 1673-1603(2017)03-0244-09