试验设计类型之单因素设计

郭春雪，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com )



试验设计类型之单因素设计

郭春雪1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu812@sina.com )

本文目的是全面介绍与单因素设计有关的问题。通过详细分析单因素设计的几种亚型和由配对设计退化而成的单组设计，全面而深入地呈现出合理选用单因素设计的要领；通过对“组别”真相的揭示，提高读者识别“假单因素设计”的能力。真正的单因素设计只涉及一个专业上可以清楚命名的影响因素，其他任何非试验因素对评价指标的影响在该影响因素各水平组之间是均衡的，其与影响因素之间的交互作用在客观上是可以忽略不计的。

单组设计；同质性；单因素K(≥2)水平设计；析因设计；正交设计

1 单因素设计中的两种或三种亚型

1.1 单因素设计之概述

在一个试验研究项目中，研究者仅关注一个影响因素，它既可能是一个试验因素，也可能是一个重要的非试验因素。它的所有水平不需要用“组别”或“分组”或“处理”或“方案”之类含糊其辞的词语才能表达清楚，而是可以方便地以不言自明的专业名称言简意赅地描述出来。例如“药物种类”“某药的剂量大小”“某药的作用时间”“抑郁症的类型”“有无自杀性意念”等。

单因素设计可分为两种亚型：即单组设计和单因素K(≥2)水平设计；但根据人们对定量数据进行统计分析方法来划分，单因素设计也可分为三种亚型：单组设计、成组设计(其学名为单因素两水平设计)和单因素K(≥3)水平设计(或单因素多水平设计)。

1.2 与单组设计有关的问题[1]

1.2.1 何为单组设计

所谓单组设计，就是研究者仅关注影响因素的一个特定水平，由它定义了一个特定的“总体”，从该总体中随机抽取一定数量的受试对象形成一个被研究的“样本”。于是，人们就称这个“样本”构成了一个单组设计下的“受试对象”。

1.2.2 单组设计隐含的前提条件

隐含的前提条件是：在单组设计中的“受试对象”相对于特定的“评价指标”而言，他们或它们应具有很好的“同质性”。

例如，假定有人发现：长期生活在海拔>3 000米山区的大部分正常成年人(假定无性别之间的差异)平均每分钟脉搏次数大约为68次，而由基本常识得知，不居住在前述特定环境下的绝大多数正常成年人平均每分钟脉搏次数大约为72次。要想通过科学严谨的试验研究，并假定“72次/分钟”为“标准值”或“理论值”，则研究者就可以依据某些先验知识估算出合适的样本含量，并只需要从长期生活在海拔>3 000米山区的正常成年人中进行随机抽样，当获得足够样本含量的受试对象并在特定的条件(如静坐半小时)下测定出他们各自的脉搏次数，这些数据就构成了一个来自单组设计的样本数据。

就上面这个例子，如何理解来自单组设计的受试对象应具备“同质性”呢？ 即只要受试对象满足“长期生活在海拔>3 000米山区的正常成年人”这个特定的前提条件，他们脉搏次数的数据波动完全取决于他们的“个体差异”，而与“性别”“家族”“血型”或其他任何可说出名称的“影响因素”无关。换言之，从专业或其他角度来考量，没有理由和任何有力的证据将来自单组设计的全部受试对象划分成两组或多组。但是，若进一步研究发现：在“长期生活在海拔>3 000米山区的正常成年人”中，“经常按一定强度锻炼身体”与“不经常按一定强度锻炼身体”的两类人，其脉搏次数之间存在明显区别，此时，前述所获得的“样本”就不具备“同质性”了，也就是说，前述的“单组设计的样本”就不成立了，而应该被称为“单因素两水平设计的样本”了。其试验因素的名称为“是否经常按一定强度锻炼身体”，它的两个水平分别为“是”与“否”。

1.2.3 单组设计中究竟有没有对照组

在“单组设计”中，似乎没有“对照组”，而没有对照的研究是没有说服力的！事实上，在“单组设计”中是有一个“隐含对照组”的(有人称其为“外部对照组”)，它就是与评价指标的标准值或理论值相对应的那个总体，而来自“单组设计的样本”应该被视为是与其自身所代表的“抽样总体”对应的“随机样本”。由此可知，在评价指标为一元定量变量时，单组设计及其一元定量资料差异性分析问题不应该被叫做“样本均值与总体均值的比较问题”，而应该被称为“一个未知总体均值与一个已知总体均值的比较问题”。

1.2.4 何时适合选用单组设计

由直观判断可知，在一个试验研究中，若选用单组设计，所需要的样本含量会相对较少。人们不禁要问：何时适合选用单组设计？由统计学中的“对照原则”可知，在绝大多数场合下，不适合也不应随意选择单组设计，这是因为通常并不存在主要评价指标的“理论值或标准值”。一般来说，仅在下列两种场合下，才可考虑或借助“单组设计”(注意：绝对不是最佳或最优选择)来设计试验：其一，找不到或不允许(例如在医学上，若设立对照组将严重违反伦理道德或实践上根本无法操作)设立对照组，但可以找到主要评价指标的“公认标准值或理论值”；其二，找不到合理的或合适的对照组，但某项试验若能获得成功，其试验研究本身的价值十分重大，同时，主要评价指标的“理论值或标准值”是客观存在的或由基本常识就可得到“公认”的。例如“换头手术”，迄今为止的理论和实践都已明确认为：“换头手术的成功率几乎为零”，于是，“0”就是“换头手术”成功率的“理论值或标准值”。若临床试验研究的成功率在统计学上被证明明显高于“0”，就表明单组设计取得了预期的效果；又例如，心脏骤停且胸腔骨折又非常严重的患者，若采用常规按压胸部的急救手术使患者心脏复苏，其成功率几乎为零(注意：腹部提压的心脏复苏仪可能是提高此种困境下心脏复苏成功率的有益尝试与实践)，此时，若想开展临床试验，在得到伦理委员会同意的前提下，也可以选用单组设计来安排试验。

1.2.5 单组设计的奇特之处

单组设计是所有试验设计类型中最简单的一种设计类型，然而，用于处理单组设计资料的统计分析方法的种类却远远多于其他任何一种设计类型资料所对应的统计分析方法。这是由于绝大多数多元(包括多因素)统计分析方法仅适用于单组设计多元定量资料或定性资料或定量与定性混合型资料，特别是聚类分析、主成分分析、因子分析、路径分析、结构方程模型分析、潜在类别分析和项目反应模型分析，甚至连回归分析(注意：人们在实际使用回归分析时并没有去关注资料是否来自单组设计，而是把定量和定性自变量全部默认为定量变量，把全部受试对象视为满足“同质性”要求，其实，这是不够妥当的)也是如此。

1.3 与单因素K(≥2)水平设计有关的问题

1.3.1 何为单因素K(≥2)水平设计

所谓单因素K(≥2)水平设计，就是在一个试验研究中，只考虑在一个影响因素(通常是试验因素，但也可以是重要的非试验因素)的两个或两个以上的水平条件下，从受试对象身上测定某些评价指标的数值，以评价该影响因素各水平对结果的影响大小及其差异性情况。例如在文献[2]中，研究者把抑郁症患者分为“单相抑郁型”“双相Ⅰ型”与“双相Ⅱ型”三类，属于单因素三水平设计问题。

1.3.2 单因素K(≥2)水平设计隐含的前提条件

隐含的前提条件是：各水平组中受试对象在其他任何非试验因素方面均衡一致，且任何非试验因素与所考察的影响因素之间对评价指标影响的交互作用在本质上是可以忽略不计的。

1.3.3 单因素K(≥2)水平设计中的对照组

一般来说，在单因素K(≥2)水平设计中可能会有两种对照形式之一：第1种，有一个“空白或标准或试验对照组”；第2种，全部K个组之间形成“相互对照”(例如考察某药物4个不同剂量疗效之间的差别)。

在一项试验研究中，由研究目的确定的影响因素只有一个且至少具有两个水平，其他的非试验因素对评价指标的影响可通过以下三个途径使其降至最低：其一，在有根据地估算出最少样本含量基础上适当增大样本含量；其二，制订严格的关于受试对象的纳入标准和排除标准，并通过完全随机的方式将全部符合纳入标准且不符合排除标准的受试对象均分入拟考察影响因素的各水平组中去；其三，当样本含量并非特别大(1 000例以上，才可被称为较大样本含量)时，应该尽可能找准找全对评价指标有影响的重要非试验因素，并按其对全部符合纳入标准且不符合排除标准的受试对象进行分层，再将各层中的受试对象随机均分入拟考察影响因素的各水平组中去。

1.4 由配对设计退化而成的单组设计

1.4.1 何为配对设计

所谓配对设计，就是与同一个定量评价指标对应的两组数据成对出现，这些成对数据有4种可能的来源：其一，来自同一个个体，故被称为自身配对设计；其二，来自母体相同的两个个体(如双胞胎)，故被称为同源配对设计；其三，来自属性因素(如性别、年龄等)取值相同或接近的两个个体，故被称为属性因素相近者配对设计；其四，来自外部环境因素(如以“夫妻”为配对条件)取值相同或接近的两个个体，故被称为外部环境因素接近者配对设计。

1.4.2 如何使配对设计退化成单组设计

上述4种形式的配对设计一元定量资料，在对其进行差异性分析时，首先要求出每对数据的差量，再求差量的平均值并与其“理论值0”进行比较。由此可知，对原始数据而言，属于“配对设计一元定量资料”；而在对其实施差异性分析时，由“差量”形成的一组数据就自动地退化成为“单组设计一元定量资料”了。

1.4.3 两种单组设计之间的区别是什么

由前面“1.3节”中介绍的“单组设计”可以被称为“标准型单组设计”；而本节中介绍的由配对设计退化而来的“单组设计”，可以被称为“退化型单组设计”。这两种“单组设计”在本质上是一样的，其区别在于：“标准型单组设计”通常存在非零的“理论值或标准值”；而“退化型单组设计”的“理论值或标准值”一定是“0”。

该功能主要面向有图书馆借阅证的校内师生，通过绑定图书证，可以将微信公众号和校园网站服务结合起来，让广大师生享有更便利、功能更全的信息服务，同时该平台也向师生开放了解绑图书证的功能，给用户更多的自主选择权。

1.4.4 如何合理选择配对的形式

在原本属于“单因素两水平设计”的试验研究中，根据该因素两个水平的具体情况，当条件允许时，选择配对设计要比选择非配对设计效果好，因为在相同样本含量的前提下，检验效能会有较大提升；换句话说，在相同检验效能的前提下，可以节省较多的样本含量。

问题是适合选用配对设计的“条件”究竟是什么？

情形一：当2水平影响因素中的一个水平为0水平时，选用自身配对设计是比较合适的。例如，某人研究出一种穴位针灸方法改善受试对象的记忆力，在使用穴位针灸前后分别检测每位受试对象的记忆力。此时，影响因素为“是否使用穴位针灸(未用与使用)”，其中，“未用”就是该影响因素的“0水平”。使用自身配对设计时，两个水平之间的“时间间隔”不应过长，因为一旦时间间隔过长，受试对象自身的体内变化和受到外界的影响都很大。

情形二：当2水平影响因素的两个水平都是非0水平，即两个水平都会产生一定效应的“真实水平”(例如在每位受试对象身上某个穴位采取针灸治疗)且已知治疗的效果明显受到“遗传因素”的影响时，选用同源配对设计的效果为好。

情形三：当2水平影响因素的两个水平都是非0水平，即两个水平都是会产生一定效应的“真实水平”且很肯定已经找准找全对评价指标有影响的重要非试验因素，同时，也能找到足够多的受试对象来按前述提及的全部重要非试验因素分别形成对子时，选用属性因素相近者配对设计是可行的。

说明：以“家庭”或“班级”或“社区”等为配对条件，实施配对设计的试验研究，其应用场合(例如研究每对夫妻智商之间是否有差异等)非常少，此处就不细究了。

2 学会识别假单因素设计的窍门

2.1 “组别”常常是假单因素设计的“套牌”

当今，人们经常会从电视新闻上看到：交警常会发现少数私人汽车后部挂着“假牌照”，甚至还出现了一些“克隆的出租车”。然而，在一些学术论文中，人们经常可以看到用统计表呈现的科研资料会以“组别”或“处理”或“方案”等笼统的词语，作为若干个试验条件或试验分组的“总称”。部分论文的作者便想当然地将自己的科研资料视为“单因素设计资料”，进而不假思索地选择单因素统计分析方法对科研资料进行差异性分析。这种以假乱真、混淆视听的做法，在学术论文中具有相当的普遍性。

下面就从学术期刊或学术论著中摘录有关案例，揭示出假单因素设计的常见表现，以便提高人们识别其真面目的能力。

2.2 “组别”是多个因素水平的全面组合

【例1】某临床医生将12例缺铁性贫血患者随机分入4个组接受不同的治疗，4种治疗方案分别列入表1的第1列“组别”之下，主要评价指标为治疗后红细胞数的增加量。见表1。

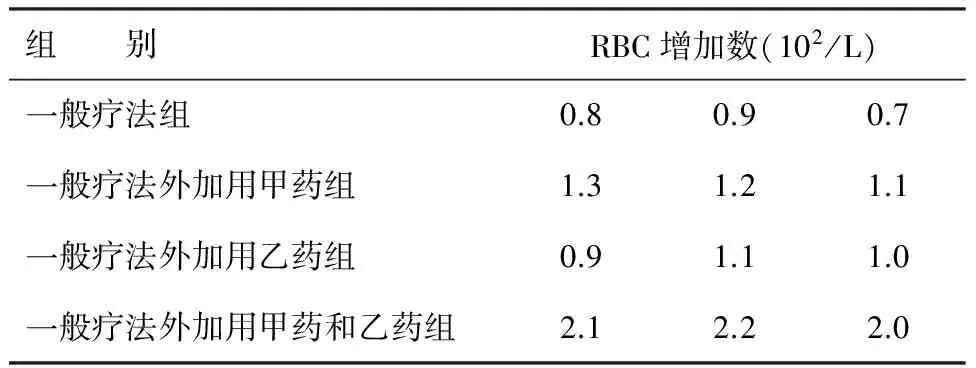
表1 4种不同疗法治疗缺铁性贫血1个月后红细胞平均增加数

剖析：首先，应当指出的是，表1中的总样本含量12是如何确定的，提供数据者似乎没有交代理论依据是什么。然而，在选择统计分析方法对表1中的资料进行差异性分析时，相当多的人将表1中的“组别”视为一个影响因素，“很自然地”选择了单因素4水平设计分析方法。事实上，此处“组别”应该是全部患者在一般疗法基础上，分别接受了4种不同处理之一的处理。这4种处理正好是两个2水平因素的全部水平组合所形成的治疗方案，即甲乙药均不用、仅用甲药、仅用乙药和甲乙药都用。它们正是“甲药用否”与“乙药用否”的全面组合。将表1改写成表2的形式，不仅概念清晰，而且与设计有关的内容(两个因素，各有两个水平且它们的水平全面组合)不言自明。

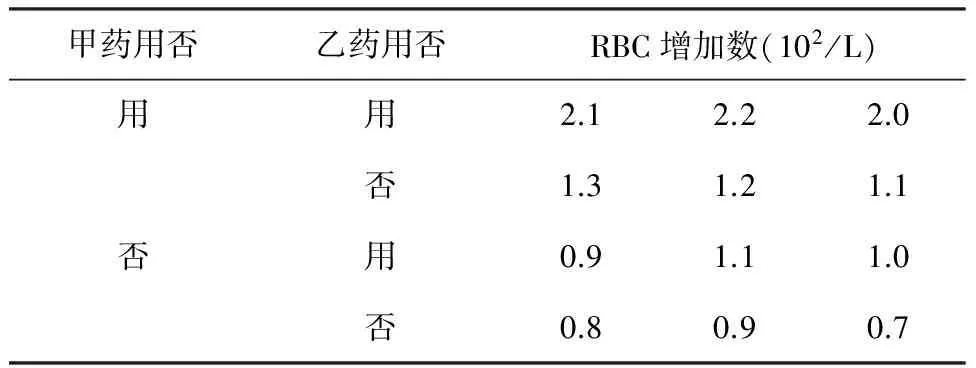
表2 4种不同疗法治疗缺铁性贫血1个月后红细胞平均增加数

容易看出：在表1中，“组别”是一个“假单因素”的“万能名称”；而在表2中，可以清楚地看出：“甲药用否”与“乙药用否”才是表1中“组别”的“真相”。当表2中的两个因素对评价指标的影响同等重要时，由这两个因素所决定的“架构”可被称为两因素析因设计。

事实上，在学术期刊或专著上，“组别”的“内容与含义”更是“千姿百态”，下面将进一步揭示其“真相”。

2.3 “组别”是多个因素水平的部分组合

2.3.1 部分组合是依据高阶交互作用分解方法从全部组合中分割出来的

在分式析因设计[3]中，被挑选出来的试验点是与其相对应的完整“析因设计”的一部分，若将这一部分试验点冠以“组别”作为其总称，当然，会给人以“假象”。这就属于“部分组合是依据高阶交互作用分解方法从全部组合中分割出来的”。

2.3.2 部分组合是依据组合原理拼凑出来的

有一种被称为组合设计[4]的方法：在因素的编码空间中选择几类具有不同特点的试验点，将它们适当地组合起来形成的试验安排。若将这些试验点冠以“组别”作为其总称，当然，也会给人以“假象”。这就属于“部分组合是依据组合原理拼凑出来的”。

2.3.3 部分组合是依据正交性原理从全部组合中挑选出来的

基于正交性原理[5]，从原本属于析因设计的全部水平组合中挑选出一部分试验点，若将这些试验点冠以“组别”作为其总称，当然，也会给人以“假象”。这就属于“部分组合是依据正交性原理从全部组合中挑选出来的”。

2.3.4 部分组合是依据均匀性准则从全部组合中挑选出来的

基于均匀性准则[6]，从原本属于析因设计的全部水平组合中挑选出一部分试验点，若将这些试验点冠以“组别”作为其总称，当然，也会给人以“假象”。这就属于“部分组合是依据均匀性准则从全部组合中挑选出来的”。

2.3.5 部分组合是依据优良性准则从全部组合中挑选出来的

基于优良性准则[7]，从原本属于析因设计的全部水平组合中挑选出一部分试验点，若将这些试验点冠以“组别”作为其总称，当然，也会给人以“假象”。这就属于“部分组合是依据优良性准则从全部组合中挑选出来的”。

2.3.6 部分组合是凭主观臆断从全部组合中盲目抓取的

【例2】某研究者在研究透明质酸(HA)及其受体在不同皮肤组织创面愈合过程中的表达及意义时，从多种不同的皮肤上取样，共形成了8个组，检测各组受试对象皮肤中HA含量，其资料格式如表3所示[8]。

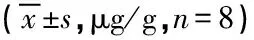
表3 几种不同标本中HA含量的检测结果

剖析：显然，表3中“组别”所代表的是一个“复合型因素”，它究竟由多少个独立影响因素的哪些水平组合而成，需要仔细推敲。这种“组别”所代表的试验安排不应被称为某种标准的多因素设计类型，而应该被称为“多因素非平衡组合试验”。原研究者将表3中的8个组冠以“组别”作为其总称，给人以“单因素8水平设计的假象”。这就属于“部分组合是凭主观臆断从全部组合中盲目抓取的”。

欲对此类定量资料进行差异性分析，需要先对“组别”进行合理地拆分，再结合分析目的、基本常识和专业知识对拆分后的某些组进行合理“组合”，具体如何操作，可参阅有关文献[8]，此处从略。

[1] 胡良平. 实用医学统计学[M]. 北京: 金盾出版社, 2014: 111-121, 183-272.

[2] 林康广, 卢睿, 陈玲玉, 等. 单双相抑郁患者的情感气质特征及其与抗抑郁治疗反应的关系[J]. 四川精神卫生, 2016,29(3): 211-215.

[3] Douglas CM. Design and Analysis of Experiments[M]. 北京: 人民邮电出版社, 2007:282-346.

[4] 任露泉. 试验优化设计与分析[M]. 2版. 北京: 高等教育出版社, 2001: 246-278.

[5] 田口玄一. 实验设计法(上)[M]. 北京: 机械工业出版社, 1987:170-325.

[6] 方开泰, 马长兴. 正交与均匀试验设计[M]. 北京: 科学出版社, 2001: 83-211.

[7] 王万中. 试验的设计与分析[M]. 北京: 高等教育出版社, 2004: 333-357.

[8] 胡良平. 统计学三型理论在实验设计中的应用[M]. 北京: 人民军医出版社, 2006: 139-165.

(本文编辑：陈 霞)

Types of experimental design: a single factor design

GuoChunxue1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China；2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

The aim of this article is to comprehensively introduce some questions related to a single-factor design for an experimental research. A detailed introduction is provided for several subtypes of a single-factor experimental design and a special case which demonstrates a single-group design degenerated from a paired-group design. This introduction intends to present the key points of accurate selection of the single-factor design type for a matched experiment in a comprehensive and in-depth way. Through revealing the true nature of a commonly used concept "group", the paper helps readers improve their ability to identify "a fake single-factor design". A true single-factor design involves only a single factor that can be clearly and scientifically identified and the effect of other non-experimental factors on the evaluation index are balanced among all levels of the factor. The interactions between it and the other influencing factors are negligible.

A single group design; Homogeneity; A single factor design with K(K≥2) levels; Factorial design; Orthogonal design

国家高技术研究发展计划课题资助(2015AA020102)

R195.1

A

10.11886/j.issn.1007-3256.2017.01.002

2017-02-11)