广义等温等压系综-分子动力学模拟全原子水的气液共存形貌∗

尹灵康 徐顺Seongm in JeongYongseok Jho 王健君 周昕†

1)(中国科学院大学物理科学学院,北京 100049)

2)(中国科学院计算机网络信息中心,北京 100190)

3)(Center for Soft and Living M atter,Institute for Basic Science(IBS),U lsan 44919,Repub lic of Korea)

4)(中国科学院化学研究所,北京 100190)

广义等温等压系综-分子动力学模拟全原子水的气液共存形貌∗

尹灵康1)徐顺2)Seongm in Jeong3)Yongseok Jho3)王健君4)周昕1)†

1)(中国科学院大学物理科学学院,北京 100049)

2)(中国科学院计算机网络信息中心,北京 100190)

3)(Center for Soft and Living M atter,Institute for Basic Science(IBS),U lsan 44919,Repub lic of Korea)

4)(中国科学院化学研究所,北京 100190)

(2017年3月29日收到;2017年5月4日收到修改稿)

探测相变过程中瞬时共存相的形貌等特征对理解其微观机制十分重要.本文应用广义等温等压系综-分子动力学模拟方法,研究全原子水模型的气液两相平衡及相变的中间过程.研究发现,此广义系综方法能够通过持续降温,连续地历经从气态、气液共存到液态的整个相变过程,通过持续升温历经其相反过程,而不会发生标准正则系综中的过饱和热滞现象.该方法不需要使用副本交换等增强抽样方法,因此可以用于较大体系的研究,多个独立的模拟即能获得整个气态液态区的平衡性质及共存相特征.本文还提出了计算气液共存界面面积的新方法,给出了水的气液共存界面形状随温度、压强的变化规律.结果表明,低压时水的气液共存界面因其较大的表面张力而接近球面,符合经典成核理论的描述,但随着压强升高接近其临界压强时,气态和液态的差别减小,界面的表面张力变小,界面形状变为无规则的枝杈结构,表现为二阶相变特征.

广义正则系综,气液相变,气液共存,分子动力学

1 引 言

气液相变是自然界中非常普遍的现象,在人类的生活生产中扮演着重要角色,然而人们对相变的微观机制并没有完全理解.描述相变过程的一般理论是经典成核理论(CNT)[1-3].CNT认为相变的发生受成核过程支配,即形成一个具有一定大小的、球形的新相的核,称为临界核,然后这个临界核迅速长大,直至整个系统完全变成新相.但是CNT对临界核的形状、结构做了过于简单的近似,不能解释很多实验现象.近来,大量工作着眼于研究相变过程中的微观细节[4-8],人们发现用多步成核理论[1,9-12]来描述许多相变成核过程可能更加精确.这些结果表明,想要清晰地理解相变过程,形成核以及核生长变大的微观细节是十分重要的.

人们发展了许多方法来研究相变成核过程[13-17]以及相共存态的微观结构[18-23]. Zahn[24]采用路径抽样技术,通过分子动力学模拟研究简单模型的水的沸腾现象,给出了液态体系中相变开始阶段气相核的形成过程.Panagiotopoulos[25]于1987年提出了Gibbs系综Monte Carlo(GEMC)方法,可以直接获得共存区的相平衡.M oučka和Nezbeda[26]以及Trejos等[27]应用该GEMC方法分别研究了BK模型水的气液平衡过程和受限量子液体的气液共存态.Cho等[28-31]对势能函数做出修改,使用广义副本交换方法,能够抽样到稳定存在的共存区的构象,研究了Lennard-Jones流体和全原子水等多种模型的两相共存形貌特征.Xu等[32]引入广义正则系综(GCE),结合副本交换技术,使用Monte Carlo (MC)方法模拟了格点Potts模型的铁磁顺磁相变共存区.Jeong等[33]应用这个GCE副本交换模拟,给出了Lennard-Jones模型和粗粒化mW水模型的气液共存相的微观形貌随温度和压强的变化.

这些相变共存态的模拟研究通常使用副本交换等增强抽样技术,因此一般集中在较小或较简单的系统.本文扩展GCE的MC模拟到分子动力学模拟(MD),研究大尺寸全原子水体系的气液转变及其共存相的微观结构.相较于MC模拟,MD方法有许多成熟的软件包可供使用,因此在研究全原子水模型等比较复杂的系统中比较方便.我们在MD通用程序包(LAMMPS,GROMACS等)中实现了广义等温-等压系综MD方法(gNPT-MD).

我们模拟了4000个TIP4P/2005水分子在不同压强下的气液相变,发现至少在压强不太低的情况下,等温-等压(NPT)系综下水的气液相变的过饱和热滞现象在广义等温-等压(gNPT)系综中被很好地消除,系统能连续地在气液两相之间转变.从而无需使用副本交换等技术,通过持续升温或降温的gNPT-MD模拟,我们就可以得到系统在整个相变区的微观构象,包括纯液态、过热液态、气液共存、过冷气态以及纯气态等,并准确地给出了气态液态间的相平衡条件.为了定量分析共存相的微观特征,我们严格定义液滴表面分子可达面积为液气共存界面面积,提出了一个较精确地计算气液两相界面面积的方法,得到了共存区内气液界面的形貌随温度、压强的变化规律.对比不同压强下共存区的构象,我们发现低压时的共存界面更接近于球面,基本符合经典成核理论,而高压时界面形状复杂,存在许多枝杈结构,表现为二阶相变的特征.计算得到的表面张力表明,高压时表面张力较小,不足以克服界面的形状涨落.

本文的组织如下：第2部分先简单地介绍了GCE的原理,gNPT-MD在模拟软件包中的实现,以及gNPT系综和NPT系综的关系,然后给出了Voronoi单胞分析方法,并详细说明我们改进的计算共存界面面积的方法,随后给出模拟的细节;第3部分,给出了用gNPT-MD方法来研究全原子水模型的气液相变及共存区界面形貌、表面张力等主要结果;第4部分给出结论.

2 研究方法

2.1 GCE与gNPT系综

相变共存区在常规系综(如正则系综NVT, NPT等)下不稳定,其微观构象不能被有效探测.广义系综能够通过使用能量依赖的热源温度(或等价地修改势能面)而有效地抽样这些共存构象.

NVT系综的构象分布函数可以写为

这里β0是倒温度,E(r)是系统势能,r是构象坐标的简单记号.在广义系综如GCE中,势能E(r)被有效势能Ug(E)代替：

其中β0,E0和α为常数参数.改变β0或E0可得到不同的GCE.α＞0对应GCE,α=0对应NVT系综.

在分子动力学模拟中实现GCE系综非常简单,只需在标准的NVT系综模拟中将热源温度替换为能量依赖的瞬时温度 T(E)=1/βg(E)[32],这里GCE的倒温度

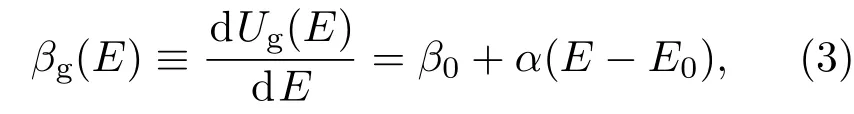
无需修改模拟程序的其他部分.这里E为当前构象的势能,因此GCE中热源温度在模拟的每一步均被重置.容易证明,这样可以得到GCE下的构象空间分布函数,P(r)∝ e-Ug(E(r)).值得注意的是,这样实现的GCE模拟仅保证构象空间内等式(2)给出的这个有效势能的分布,其在动量空间的分布不是任何温度下的Maxwell-Boltzmann分布.

在gNPT系综中,等式(2)中的势能E用焓H=E+PV代替,有效势能可以写为

这里P和V分别是外部压强和系统体积,H0是常数.同样可以有gNPT系综中焓依赖的热源倒温度：

在任意标准分子动力学软件包中,实现gNPT系综与实现GCE类似,即通过等式(5)计算当前构象的H对应的热浴的瞬时温度.值得注意的是,在计算系统当前构象压强以耦合目标压强时,系统压强中理想气体部分的贡献由当前重置后的热浴温度直接给出,不使用系统当前的动能来计算,而系统瞬时压强中的维里部分无需任何改变.

2.2 gNPT系综与NPT系综的关系

我们以gNPT与NPT系综为例说明广义系综与正则系综的关系,GCE和NVT系综的关系基本类似.任意系统的构象空间性质由其态密度eS(H),或者内禀倒温度函数

确定,这里S(H)是熵函数.对gNPT系综,热源倒温度βgNPT(H)和内禀倒温度曲线βs(H)的交点给出H空间分布的极值点.如果此处βgNPT(H)的斜率比βs(H)的切线的斜率大,则为分布的极大值点,即该gNPT系综主要访问这个附近.对较大的α,这个极大值点惟一,近似等于此gNPT系综下H的平均值.

图1给出了典型的相变系统的βs(H)曲线.对NPT系综,热源倒温度与H无关,对应斜率为0的水平直线,而gNPT系综的热源倒温度为斜率为α的直线.在相共存温度区间,每个NPT系综的倒温度线与 βs(H)有三个交点,如图中A,B和C点.但仅纯相或过饱和相(A和C)是概率分布的极大值点,能在此NPT系综中被充分访问,而共存相B是分布的极小点,仅有非常小的访问概率,归因于B点处βs(H)曲线的正斜率.在NPT系综中,在降温和升温过程中,系统分别从气态到液态以及从液态到气态的相变的βs(H)-H曲线不重合,而是存在热滞现象,如图中带箭头的红色虚线所示.因此通常的NPT模拟很难准确地给出两相共存温度,难以有效地探测两相共存的焓区(内禀倒温度的正斜率区)的微观构象.而这些共存构象对应不同温度的NPT系综中相变发生的过渡态,对理解相变微观机制十分关键.在gNPT系综中,当热源倒温度函数的斜率α大于系统内禀倒温度曲线在共存区域的斜率时,每个gNPT系综的倒温度线与βs(H)只有一个交点,因此共存构象能被充分抽样.

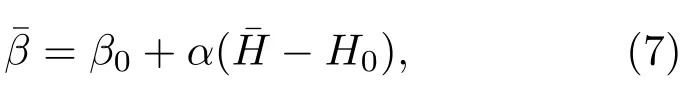
可以给出系统内禀倒温度曲线 βs(H)上的一点(,).改变β0(或者H0)的值,gNPT系综可以充分抽样系统任意焓区的微观构象,给出整个βs(H)曲线,并能够积分得到熵函数S(H).

图1 (网刊彩色)典型的相变过程的倒温度曲线βs(H)与自由能曲线 最上方的蓝色曲线是相变过程的倒温度曲线,红色虚线是NPT系综给出的相变曲线,红色直线为NPT系综和gNPT的热源倒温度线,下方三条蓝色曲线分别给出了T1,Tc,T2三个温度下的自由能曲线(β=1/kB T)Fig.1.(color on line)Typical cu rves of the recip rocal of temperature of phase transitionβs(H)and cu rves of free energy:The b lue cu rve on the top rep resent βs(H)of typical phase transition,the red dashed lines correspond to phase transition of NPT ensem b le,the red fu ll lines correspond to the recip rocal of temperature of NPT ensem b le and gNPT,and the other b lue curves show the free energy at T1,Tc,T2(β=1/kB T).

由此我们容易得到任意温度T下NPT系综的H空间分布,PNPT(H)∝e-H/T+S(H),以及自由能,

这里S(H)由变化参数β0而得到的一系列gNPT系综下的平均焓及对应的给出的βs(H)曲线积分得到,

S(H)依赖于系统外部压强P.对每个压强下的曲线 βs(H),我们可以确定共存温度 Tc,使得βc=1/Tc与 βs(H)所包围的上下两部分面积相等,即图1中两个阴影部分面积相等.此时气液两相的自由能相等,自由能曲线的能垒由表面能提供.一般地,对任意温度和压强,自由能能垒为,

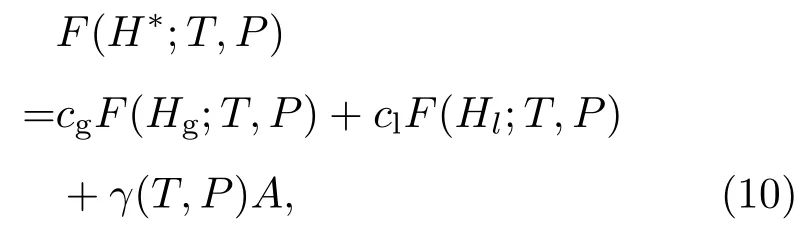
这里cg和cl分别是能垒H∗处气态和液态分子的比例,可由H∗=cgHg+clHl以及cg+cl=1给出;Hg和Hl分别是此温度、压强下气态和液态的平均焓值;γ(T,P)是界面张力,A是界面面积.我们可以由此计算出界面的表面能及表面张力[34,35].

2.3 Voronoi单胞分析方法

Voronoi单胞[36-38]是一种重要的分析工具,可以解决一些随机介质中的结构分析问题,如玻璃、多胞固体、蛋白质等.把空间中任意一点与其他点相连,所有连线的垂直平分面可以包围成一个封闭的多面体,这个多面体称为Voronoi单胞. Voronoi单胞可以把一个封闭空间划分成许多充满空间、但不交叠的凸多面体.在本文中,我们通过Voronoi单胞分析方法来分析模拟结果,通过每个水分子的Voronoi单胞体积来区分水分子属于液态还是属于气态.

我们可以计算得到所有分子的Voronoi单胞体积,然后统计纯气态相和纯液态相中分子的Voronoi单胞体积的分布,得到区分气态和液态的一个临界值.通过此值可以判断相变过程中每个分子的状态(气态还是液态),分子的Voronoi单胞体积大于此值,认为此分子是气态分子,小于此值认为是液态分子.

当两个分子共有同一个Voronoi面时,认为这两个分子是近邻分子.当两个近邻分子处于同一相(气相或液相)时,认为这两个分子属于同一个聚集体.由Voronoi方法可以给出每个分子的近邻分子数,以及两个近邻分子的界面面积等值.通过此方法我们可以获得体系中液相聚集体(液滴)、气相聚集体(气泡)的数目,每一个液滴、气泡的体积大小和所包含的分子数等微观信息.

2.4 形状因子

为了定量地描述相变过程中气液两相界面的形貌特征,我们计算了序参量形状因子[33]

其中A是液相和气相界面的总面积,A0l(A0g)是与体系中所有液滴(气泡)总体积相等的球体的表面积.因此,为了尽可能准确地估计聚集体的形状,我们需要尽量精确地计算两相分子所占的体积及其界面面积.虽然Voronoi单胞方法可以得到两相分子的体积及其界面的面积,但是此界面是由多个二维平面拼接而成,形成的不是一个光滑的表面,而是一个锯齿状的粗糙表面,这样求得的界面面积会偏大.

因此我们使用另一种方法来计算界面面积.液滴是由多个液态水分子堆积而成的凝聚体,计算液滴的表面积就类似于计算蛋白质等物质的溶液可接触面积.把液滴中的水分子视作质点,用两个半径分别为r1和r2(r2＞r1)的探测小球,在液滴表面滚动,两个探测小球的质心经过的区域会形成一个封闭的厚度为d=r2-r1的壳层结构,这个壳层结构就是两相的界面区域.界面区覆盖的面积依赖于两个探测小球的半径大小,探测小球半径如果太小,可能会掉入液滴内水分子的缝隙中,使得界面区比较粗糙;太大则不能很好地描述界面的形状.通常r1应该比水分子半径稍大,近似为液滴内分子的平均距离尺度.厚度d应该远小于液滴的外表面曲率半径,此时界面区与液滴的接触面积和与气泡的接触面积近似相等.因此只要求得界面区的体积Vinter,就可以近似得到界面区覆盖在液滴上的面积A=Vinter/d.

我们均匀分割模拟体系来计算体系中气相区、液相区和界面区的体积.把模拟盒子等分成许多个小网格,判断每个格点处于气态区、液态区还是界面区,根据每个区域的格点数目来计算其体积.网格尺寸相对厚度d较小时,体积的计算可以非常精确.考虑到计算量的大小,选定划分的网格的数目,根据网格大小给定界面区厚度d.

用每个网格的中心点坐标表示此网格的位置,可以计算出每个格点与每个液态水分子的距离,并求出每个格点与水分子的最小距离,当其最小距离小于r1时,此格点处于液态区域,当其大于r2时,此格点处于气态区域,介于两者之间表明格点处于界面区.我们给出了界面区面积以及形状因子对r1的变化曲线,如图2所示.

从图2中可以看出,随着r1的增大,界面区覆盖在液滴上的面积先快速减小,后线性增加,而形状因子的减小趋势逐渐变缓.当r1很小时,处于液态区域的点可能被判断为处于界面区或者气态区,液滴内存在一些空洞和凹陷,导致界面区面积被过度估计.随着r1的增大,这些空洞和凹陷消失,界面区域开始变得光滑.进一步增加r1导致界面面积线性增加.此时的r1能较好地给出界面特征,形状因子也处于缓慢减小的区域.

图2 (网刊彩色)形状因子(a)和界面区覆盖液滴的面积(b)随参数r1的变化Fig.2.(color on line)Shape factor(a)and interface area(b)as a function of param eter r1.

本文中,把模拟体系的x,y,z三个维度均等分成101份,即把整个模拟盒子均分成约1013≈106个小网格,每个网格远小于水分子的体积.界面区的厚度与小网格的边长相等,可以保证界面区被网格完全充满.r1的值在界面面积线性增加的起点附近,为4.3Å,比水分子尺寸稍大,符合预期.

2.5 模拟细节

本文全部模拟工作由LAMMPS分子动力学模拟软件[39]实现的gNPT-MD方法完成.选用全原子水模型TIP4P/2005[40,41],体系中共包含4000个水分子.通过PPPM方法[42]来计算长程相互作用,库仑相互作用和Lennard-Jones相互作用的截断半径均为9.0Å.当原子移动超过1.0Å时,更新近邻列表.通过Nosé-Hoover温度控制器和压强控制器[43,44]控制温度和压强,选用了30,55,135 atm三个压强值.模拟的时间步长选用2 fs,x,y,z三个方向均采用周期性边界条件.

从水的标准液态构象出发,在gNPT系综中模拟持续升温过程(减少β0或增加H0). 高压(135 atm)下,每个温度点模拟8 ns,低压(30 atm, 55 atm)下每个温度点模拟14 ns.用水的标准气态构象作为初始构象进行降温过程的模拟,同样依次模拟各个温度点,每个温度点的模拟时长与升温过程相同.均取最后2 ns的数据进行分析.

3 结果与讨论

gNPT-MD能够有效地探测全原子水模型的气液相变过程,抽样到热力学不稳定的共存区构象.图3给出了不同压强下气液相变的T-H曲线,每一个压强下都有两条模拟曲线,分别为气态到液态的相变(降温)和液态到气态的相变(升温).我们通过gNPT系综得到的结果显示,升温、降温两条T-H曲线重合,即正则系综下气液相变过程中的热滞现象消失,表明在gNPT系综中,体系能连续地在两相间转变.曲线共分为三个区域：曲线左侧,温度随着焓值的增大而升高,此时体系处于纯液相;曲线右侧,温度随着焓值的增大同样逐渐升高,此时体系处于纯气相;曲线中间部分,温度随着焓值的增大而降低,此时体系处于两相共存状态.从而,不仅是纯气体、液体相、过饱和区、spinodal点以及相共存区的微观构象都能在gNPT系综中充分给出.图中黑色虚线是30 atm下NPT系综中的相变曲线,通过持续升温依次模拟各温度点得到液相到气相的转变(向右箭头),通过持续降温得到气相到液相的转变(向左箭头),两条曲线不重合,表示这里存在热滞现象.在纯气态区和纯液态区,NPT系综的结果与gNPT系综的结果相符,但进入过饱和区后,非常快速地通过共存区而不能充分给出两相共存的构象.而且由于热滞的存在,这种持续升降温的NPT系综模拟不能准确地给出两相共存温度等相变的热力学性质.

图3 (网刊彩色)不同压强下温度T随平均焓值的变化 空心圆圈表示气态到液态的相变过程,实心星号表示液态到气态的相变过程.彩色实线表示gNPT系综给出的结果,带“×”号的黑色虚线表示30 atm下NPT系综模拟结果,向右箭头表示其升温过程,向左箭头表示其降温过程.右侧给出了30 atm下相变过程中的构象图,红色小球表示液态水分子,灰色小球表示气态水分子Fig.3.(color on line)The temperatu re as a function of average enthalpy under d iff erent p ressu res:Hollow circles correspond to transition process from gas to liquid,and solid asterisks correspond to the opposite process,the colourfu l solid lines correspond to the resu lts of gNPT ensem b le,the b lack dashed lines with“×”rep resent the resu lts of NPT ensem b le at 30 atm,and the right arrow corresponds to the resu lt of heating process and the left arrow corresponds to the resu lt of cooling process.The con figurations of phase transition at 30 atm are shown on the right,the red balls rep resent liquid-like m olecu les,and the gray balls rep resent gas-likem olecules.

从图3中可以看出,低压时,一阶相变特征明显,气液两相的spinodal点的焓值相差较大,当压强接近TIP4P/2005水模型的临界压强时,一阶相变特征趋于消失,两相过渡更加光滑.随着压强的增大,水能达到的过热温度逐渐升高,这是因为在高压时,液态水克服压强效应变成气态,所需要的能量更多.

图3右侧给出了30 atm时从气态到液态的相变过程中的构象图.A点处于纯气相区域,此时体系中所有分子均为气相分子,用灰色小球表示.随着温度降低,从纯相区经过过饱和区到达spinodal点(B点)附近时,体系中开始出现液相分子,用红色小球表示.在气液共存区,液态水分子聚集成多个液滴,随着H值的下降,液滴融合变大,浸在连通的气泡中,如C,D两点.在D点,体系中的气相和液相互相分离,几乎所有液滴融合成一个大液滴.在液态的spinodal点(E点)时,整个体系基本处于液态,其中包含有多个小气泡.F点处于纯液态区,所有水分子均为液相分子,然而构象中仍有几个气态分子存在,可能是Voronoi单胞方法区分气相和液相时产生的误差.

在D,E两点之间存在着从单个连通的气泡到多个离散的小气泡的急剧变化,这种变化随着压强的降低而更加显著.这两种构象的焓值比较接近,但拓扑结构却存在很大差别,表明低压时,这里似乎对应一个结构的转变.

为了定量地描述相变过程中液滴、气泡数目、大小、形状和拓扑结构等,基于Voronoi单胞分析方法,我们计算了如下几个参数,如图4所示.最上方的曲线是相变区βs(H)曲线,中间的部分给出了较大的液滴、气泡的数目(水分子数大于3的聚集体),最下方的曲线给出了最大的液滴、气泡所含的水分子的数目.

在气态到液态的相变过程(即焓值减小的过程)中,在气态的过饱和区,spinodal点附近,液滴的数目开始增多,而且压强越大,液滴数目越多.进入共存区后,随着焓值的减小,液滴的数目逐渐减少,最后全部液滴连通成一个.在液态spinodal点附近,直到液态过饱和区,气相分子不再连通,以多个小气泡的形式出现.图中的红色虚线与倒温度曲线围成的上下两块区域的面积相等,虚线对应的温度就是正则系综下的共存温度.虚线与βs(H)曲线在共存区的交点是自由能能垒的位置,近似对应此共存温度下的临界核位置.

图4 (网刊彩色)不同压强下相变的βs(H)曲线(a),较大液滴(气泡)的数目(b),最大液滴(气泡)所含的分子数(c)随平均焓值的变化Fig.4.(color on line)Cu rves ofβs(H)under d iff erent p ressu res(a),the num ber of bigger clusters of gas(red)and liquid(green)(b), the num ber ofm olecu les in the biggest cluster(c)as functions of average enthalpy under d iff erent p ressu res.

图5 (网刊彩色)不同压强下形状因子在两相共存区随平均焓值的变化,下面的图片给出了共存温度点附近A,B, C三点的构象图Fig.5.(color on line)Shape factor dependence of average enthalpy at phase-coexisting area under different p ressures.The snapshots below show the con figu rations of A,B and C of cu rves around coexisting temperatu re.

我们计算了最大的液滴或者气泡的形状因子,结果如图5所示.形状因子值越小,越接近于1时,聚集体的形状越接近球形;值越大,越远离球形,聚集体表面越粗糙.A,B,C三个点分别对应三个压强下气液相变过程中共存温度处的临界核位置,其形状因子的值随着压强的升高而增大.图下方给出了三个点的构象图,可以直观地看到体系中聚集体的形状：30 atm时,液滴非常接近球形;55 atm时,最大液滴的表面变得粗糙,开始出现一些分枝结构;135 atm时,最大液滴完全散落在整个体系中,全部是枝杈结构,完全远离了球形.因此低压时,临界核近似于球形,近似符合CNT的假设,而高压时的状态已经背离了CNT的描述.

图6 (网刊彩色)共存温度(a)及表面张力随压强的变化(b) 图中黄色方块表示文献[35]的结果,蓝色菱形表示文献[41]给出的结果,黑色星号表示文献[45]中给出的结果,红色圆圈表示此工作的结果.Fig.6.(color on line)Coexisting temperatu re(a)and su rface tension(b)dependence of p ressu res.The resu lts of Ref.[35](yellow square),Ref.[41](b lue d iam ond),Ref.[45](black star)are shown and the red circles correspond to the resu lts of this work.

表面张力的大小决定了临界核对球形的偏离,我们计算了三个压强下的共存温度,并给出了此共存温度处的表面张力,如图6所示, 30,55,135 atm三个压强下的共存温度分别为534.0,572.0,634.0 K.文献[35,41,45]中给出了TIP4P/2005水模型在NVT系综下的临界点附近的温度变化,并根据压强张量得到了相应的系统压强,文献[45]中还给出了包括2740个水分子的体系的表面张力随温度、压强的变化.我们模拟得到的共存温度随压强的变化与文献的结果基本相符,计算得到的表面张力也近似符合文献中的结果.我们的结果表明高压时气态和液态的密度接近,气液两相的表面张力很小,液滴的形状因涨落会出现许多枝杈结构.低压时气态和液态的密度相差较大,表面张力较大,液滴近似为球形.

4 结 论

为了研究气液相变过程中气液共存状态下的微观细节,我们通过把倒温度改为焓依赖的函数的方式,给出了广义的等温-等压系综,然后在分子动力学标准软件包中实现了gNPT-MD方法.此方法不需要使用副本交换等技术就可以模拟复杂的大系统的相变过程,能有效地抽样得到热力学不稳定的共存区的构象.基于此方法,我们模拟了全原子水模型TIP4P/2005在不同压强下的气液相变过程.

可以发现,用gNPT-MD得到的纯气态和纯液态区的相变曲线能与常规NPT系综下得到结果很好地符合,而且gNPT-MD方法的结果消除了NPT系综中的过饱和热滞现象,能够给出稳定存在的共存区的构象.低压时,相变曲线具有明显的一阶相变的特征,随着压强的升高,在接近模型的临界压强的高压时,一阶相变特征逐渐消失,相变开始具有二阶相变特征.

通过Voronoi单胞分析方法,我们分析了相变过程中形成的气泡、液滴的变化,发现在气态spinodal点附近,液滴的数目随着压强的升高而增多.我们改进了计算气液两相界面面积的方法,通过计算液滴的表面可达面积的方法,得到了更加精确的面积值.计算了序参量形状因子fs,来描述体系中聚集体的形貌特征,发现共存区的微观结构在不同压强下存在着明显的差别.本文的结果表明：低压时气液两相的密度相差较大,因此表面张力较大,临界核能被维持成一个有限的球形,此时的形状因子值较小,更接近1;高压时气态和液态的spinodal点非常接近,气液两相界面的表面张力很小,临界核会出现许多枝杈结构,远离了球形,此时的形状因子值较大.

感谢中国科学院物理研究所杨成博士及中国科学院大学物理学院张传彪的讨论与帮助.

[1]Erdem ir D,Lee A Y 2009 Acc.Chem.Res.42 621

[2]Sleu telM,Lu tsko J,van D riessche A E,Du rán-O livencia M A,M aes D 2014 Nat.Comm un.5 5598

[3]Auer S,Frenkel D 2004 Annu.Rev.Phys.Chem.55 333

[4]Toxvaerd S 2015 J.Chem.Phys.143 154705

[5]Debenedetti P G 2006 Nature 441 168

[6]Gasser U,W eeks E R,Schofield A,Pusey P N,Weitz D A 2001 Science 292 258

[7]Yasuoka K,M atsum oto M 1998 J.Chem.Phys.109 8451

[8]Yasuoka K,M atsum oto M 1998 J.Chem.Phys.109 8463

[9]M yerson A S,Trout B L 2013 Science 341 855

[10]Savage J R,D insm ore A D 2009 Phys.Rev.Lett.102 198302

[11]Sleu telM,van D riessche A E 2014 Proc.Natl.Acad.Sci. 111 E546

[12]de Yoreo J 2013 Nature M ater.12 284

[13]Yarom M,M arm ur A 2015 Adv.Colloid In terface Sci. 222 743

[14]Duška M,Něm ec T,H rubyJ,V inšV,P lankováB 2015 EPJW eb Conf.92 02013

[15]Schenter G K,K athm ann SM,Garrett B C 1999 Phys. Rev.Lett.82 3484

[16]Reguera D,Reiss H 2004 Phys.Rev.Lett.93 165701

[17]Bhim alapuram P,Chakrabarty S,Bagchi B 2007 Phys. Rev.Lett.98 206104

[18]Rane K S,M u rali S,Errington J R 2013 J.Chem.Theory Com put.9 2552

[19]PlankováB,VinšV,H rubyJ,Duška M,Něm ec T,CelnyD 2015 EPJW eb Conf.92 02071

[20]M cG rath M J,K uo I F W,Ghogom u J N,M undy C J, Siepm ann J I 2011 J.Phys.Chem.B 105 11688

[21]M alolepsza E,K im J,K eyes T 2015 Phys.Rev.Lett. 114 170601

[22]Kuo IF W,M undy C J 2004 Science 303 658

[23]Nagata Y,Usui K,Bonn M 2015 Phys.Rev.Lett.115 236102

[24]Zahn D 2004 Phys.Rev.Lett.93 227801

[25]Panagiotopou los A Z 1987 M ol.Phys.61 813

[26]M oučka F,Nezbeda I 2013 F luid Phase Equilib.360 472

[27]Trejos V M,Gil-V illegas A,M artinez A 2013 J.Chem. Phys.139 184505

[28]Cho W J,K im J,Lee J,Keyes T,Straub J E,K im K S 2014 Phys.Rev.Lett.112 157802

[29]K im J,Keyes T,Straub J E 2010 J.Chem.Phys.132 224107

[30]M ałolepsza E,Secor M,K eyes T 2015 J.Phys.Chem. B 119 13379

[31]Lu Q,K im J,Straub J E 2013 J.Chem.Phys.138 104119

[32]Xu S,Zhou X,Ouyang Z C 2012 Comm un.Com put. Phys.12 1293

[33]Jeong S,Jho Y,Zhou X 2015 Sci.Rep.5 15955

[34]G loor G J,Jackson G,B las F J,de M iguel E 2005 J. Chem.Phys.123 134703

[35]Vega C,de M iguel E 2007 J.Chem.Phys.126 154707

[36]K um ar V S,K um aran V 2005 J.Chem.Phys.123 114501

[37]Zhu H X,Thorpe S M,W ind le A H 2001 Philos.M ag. A 81 2765

[38]Oger L,Gervois A,Troadec J P,Rivier N 1996 Philos. M ag.B 74 177

[39]P lim p ton S 1995 J.Com put.Phys.117 1

[40]Abascal J L,Vega C 2005 J.Chem.Phys.123 234505

[41]Vega C,Abascal J L F,Nezbeda I 2006 J.Chem.Phys. 125 034503

[42]Beckers J V L,Lowe C P,de Leeuw S W 1998 M ol. Sim u l.20 369

[43]NoséS 1984 J.Chem.Phys.81 511

[44]Hoover W G 1985 Phys.Rev.A 31 1695

[45]Alejand re J,Chapela G A 2010 J.Chem.Phys.132 014701

(Received 29 March 2017;revised manuscript received 4 May 2017)

Vapor-liquid coexisting morphology of all-atom water model through generalized isothermal isobaric ensemble molecular dynamics simulation∗

Yin Ling-Kang1)Xu Shun2)Seongm in Jeong3)Yongseok Jho3)Wang Jian-Jun4)Zhou Xin1)†

1)(School of Physical Sciences,University of Chinese Academ y of Sciences,Beijing 100049,China)
2)(Com pu ter Network Inform ation Center,Chinese Academ y of Sciences,Beijing 100190,China)
3)(Center for Soft and Living M atter,Institute for Basic Science,IBS,U lsan 44919,Repub lic of Korea)
4)(Institu te of Chem istry,Chinese Academ y of Sciences,Beijing 100190,China)

Exp loring the atom-scale details such asmorphology of coexisting phase during phase transitions is very im portant for understanding their microscopic m echanism.While most theories,such as the classic nucleation theory,usually over-sim p lify the character of the critical nucleus,like the shape,structure,and most current experiment techniques are hard ly to cap ture the instantaneousmicroscopic details,the atomistic molecular dynamics(MD)or Monte Carlo(MC) simulation provides a promise to detect the intermediate process of phase transitions.However,the standard canonicalensemble MD/MC simulation technique can not sufficiently sample the instantaneous(unstable in therm odynam ics) coexistent phase.Therefore,the MC in the general canonical ensemb le,such as general isothermal-volume ensemble (gNVT),combined with the enhanced sampling techniques,such as the rep lica exchange(RE)method,was presented to stabilize then to su ffi ciently sam p le the atom ic con formations of the phase coexistence.Due to the lim it of the RE, the RE-MC simulation on gNVT is usually app lied in sm aller system s.In this paper,we fi rst extend the gNVT-based MC simulation to the MD in the generalized isothermal-isobaric ensemble(gNPT)and very simplyimplement it in the standard atomic MD soft packages withoutm odifying the code,so that we can use these packages in MD simulation of realistic systems.Then we simulate the vapour-liquid phase transition of all-atom ic water model.At least at not very low pressures,we find that the individual gNPT simulation is already enough to reach equilibrium in any region of the phase transition,not only in the normal liquid and vapour regions,but in the super-saturation regions,and even in the vapour-liquid coexistent regions.The obtained energy-temperature curve in the cooling gNPT wellm atches with that in the heating procedure without any hysteresis.It indicates that it is not necessary to use the RE technique in the gNPT,and the interm ediate states during phase transitions in larger system s can be effectively simulated by a series of independent individual gNPT-MD simulations in the standard soft packages.We also p ropose a method to accurately determ ine the interface between the two phases in the coexistence,then provide a quantitativem easurement about the interface tension and themorphology of the coexistent phase in the larger all-atomic water at various temperatures and pressures.The results show that the liquid droplet(or vapour bubble)at the low pressure is close to a spheredue to the larger interface tension,as expectation of the classic nucleation theory of the first-order phase phase transition,but becom esm ore and m ore irregu lar as the decrease of the interfacial tension as increasing the pressure to approach to the critical p ressure,where the phase transition is the second order one.

generalized canonical ensemble,gas liquid transition,gas liquid coexistence,molecular dynam ics

PACS:61.20.Ja,64.60.Q-,64.70.F-,31.15.xv DO I:10.7498/aps.66.136102

∗国家自然科学基金(批准号:11574310)资助的课题.

†通信作者.E-m ail:xzhou@ucas.ac.cn

PACS:61.20.Ja,64.60.Q-,64.70.F-,31.15.xv DO I:10.7498/aps.66.136102

*Pro ject supported by the National Natural Science Foundation of China(G rant No.11574310).

†Corresponding author.E-m ail:xzhou@ucas.ac.cn