畸形波电磁散射特性分析及其特征识别标识的研究∗
吴庚坤 宋金宝 樊伟
(浙江大学海洋学院物理海洋研究所,舟山 316000)
畸形波电磁散射特性分析及其特征识别标识的研究∗
吴庚坤 宋金宝 樊伟†
(浙江大学海洋学院物理海洋研究所,舟山 316000)
(2016年12月30日收到;2017年4月25日收到修改稿)
针对弱非线性的Longuet-Higgins模型在模拟强非线性畸形波海面时所存在的问题,采用修正的相位调制法模拟一维畸形波时间、空间波面,该方法能够实现畸形波的定时定点生成,并且其波形既能保持目标谱的频谱结构,又能较大程度地满足波浪序列的统计特性.同时,基于改进的双尺度(TSM)法及时域有限差分法建立畸形波的电磁散射模型,经过相对平均偏差和均方根偏差误差分析后,基于TSM法研究分析了畸形波及其背景海面波的归一化雷达散射截面(NRCS)的计算结果.实验表明,合成孔径雷达成像中畸形波的NRCS比背景波要小,即畸形波的合成孔径雷达图像成像比背景波要灰暗,因此可以将NRCS作为畸形波的特征识别标识.通过分析研究不同极化方式、入射角、入射频率条件下畸形波与背景波面的电磁散射特性实验数据得出:当二者的NRCS差值大于-11.8 dB及以上时,即认为产生畸形波,这为实际的工程应用提供了参照标准.
畸形波,相位调制,电磁散射,识别标识
1 引 言
畸形波(freak wave)是随机波列中一种极其特殊的单个强非线性异常波现象,其具有能量集中、持续时间短、破坏力强等特点[1].海洋观测资料显示,畸形波遍布世界各大海域,其生成、发生具有突然性,几乎难以预测.同时,伴随着畸形波现象的出现,连续大波(three sisters)和海水深洞(hole in the sea)等异常波现象也会接踵而至,对海洋工程结构和海上作业船舶等构成巨大威胁[2,3].鉴于此,国内外学者对畸形波的研究越来越多,相关部门还组织设立了专门的研讨会(Rogue Waves Workshop)和研究项目(M ax Wave).对于畸形波资料的研究观测,大致是从以下三个方面展开的:畸形波的描述与观测方法,畸形波的生成机制与模拟方法,畸形波监测与预警.畸形波的生成机制研究方面,目前国际上普遍认为畸形波是由不同方向、不同频率特性的波浪在某一固定时间空间点的能量聚焦,同时,其各方向传播的波浪也受到海底地形折射效应、波列频散自聚焦、流场调制等的相互作用.Benjam in等首先提出等振幅的斯托克斯周期波在波列演化过程中存在不稳定性(B-F不稳定性);而后Dysthe,Peterson,Zakharov等在此基础上基于水孤波数学模型Korteweg-de Vries方程、Kadom tsev-Petviashvili方程以及多重尺度三阶非线性薛定谔方程等深入研究了近海畸形波的发生和发展机制;其后,Sundar,Clauss,Sparboom, Mori等多位学者也基于此前的理论依据在畸形波的数值模拟方面取得了众多的研究成果,其中Kim等[4]更是直接模拟出了经典的实测“新年波”序列.国内方面,基于Longuet-Higgins模型和K riebel提出的部分波数瞬态波加随机背景波模型,裴玉国等[5,6]、黄国兴[7]、刘晓霞等[8]将双波列聚焦理论模型扩展到三维模型中进而研究畸形波的生成演化规律;Zhao等[9]、Liu等[10]分别改进了调制聚焦的理论模型,在固定的时间、空间模拟出了畸形波波形;其后,一些学者基于调制不稳定性理论对畸形波演化及其数值模拟进行了相关研究;Zhang等[11,12]基于伪谱数值理论以及修正的四阶非线性薛定谔方程模拟了非线性数值波浪并分析研究了其与实验室仿真数据的对比结果.
实际工程研究中,我们可以尝试通过数值模拟畸形波的一维、二维空间波面,然后对其电磁散射模型进行数值计算和分析,来研究畸形波的形成机理、遥感识别等一系列相关特性.具体而言,我们可以基于畸形波电磁散射数值模拟的理论结果,对比分析畸形波发生海面中畸形波的SAR成像与其对应的背景波海面SAR成像,进而探索畸形波的遥感识别技术,判断畸形波的发生、发展.目前,国内外有关于这一领域的研究相对较少并且有很大的局限性,例如Franceschetti等在双尺度模型(TSM)和Harger分布表面模型的基础上改进了海面模型以用于合成孔径雷达(SAR)模拟,但这种方法并没有充分考虑速度聚束效应和畸形波波高分布的强高斯统计特征[13].本研究工作针对工程应用中弱非线性的Longuet-Higgins模型在模拟强非线性畸形波海面时所存在的实际问题,采用相位调制的方法来模拟畸形波时间、空间波面,使其能够实现畸形波的定时定点生成,并且其波形既能保持目标谱的频谱结构,又能较大程度地满足波浪序列的统计特性.同时,基于数值模拟的实验结果,结合电磁散射理论对经典的双尺度法进行改进,以构建适应于上述畸形波仿真海面的电磁散射模型,对比分析畸形波空间波面与背景波波面的散射系数的区别,进而从理论上分析畸形波波面的散射特性及其特征标识.
2 数值仿真模型
2.1 畸形波的仿真模型
在模拟不含畸形波的普通随机波浪时所采用的理论方法是Longuet-Higgins模型[14],其将大量随机余弦波进行线性叠加来表示在任意时刻某固定位置的波面方程,

上述表达式中,M表示组成波波数;ki,ai,θi和ωi分别表示组成波中i个波的波数、振幅、随机相位和角频率;η(x,t)为离波面边界距离为x的波面波动时间序列.当组成波数M所有波的初始相位在范围(,2π)范围随机取值时则生成普通随机波浪.而如果想要实现畸形波的模拟,即在某一时刻地点的随机波浪中激发畸形波波形就必须使此时间空间的随机波浪能量聚焦.基于Longuet-Higgins模型的表达式,我们采用调制波数M中部分组成波的随机初始相位,以此实现随机波浪序列中畸形波的模拟,因为只是调制了其中的部分组成波,所以可以在较大程度上使天然海浪与模拟随机波浪在统计特性方面保持一致并保持目标海浪谱的结构.具体相位调制如下:假定t=tc,x=xc的时间空间条件下畸形波产生,则我们对部分组成波的随机相位θi进行调制,使时间波面ηi(xi,ti)取正值,即将(1)式改写为背景波和畸形波的叠加波面,

当kixc-ωitc≥ 0时,(令N=int[(kixcωitc)/2π])得出随机相位θi的随机取值范围为

上述θi的取值依据具体说明如下:首先假定前提条件kixc-ωitc≥0,通过向下取整函数int运算后,int(kixc-ωitc)是比kixc-ωitc稍小的正整数(且二者差值小于1),即2π∗int[(kixc-ωitc)/2π]是比kixc-ωitc稍小的正整数,也即2π∗N是比kixc-ωitc稍小的正整数,则kixc-ωitc-2Nπ就落在了象限(0,π/2)范围内(前提条件kixcωitc≥ 0),此时,要想使cos(kix-ωit+θi)取值为正,即cos(kixc-ωitc-2Nπ+θi)为正,需要对随机相位θi的取值范围进行限定,而由上可知kixc-ωitc-2Nπ落在了象限(0,π/2)范围内,则只需规定θi在(3π/2,2π)范围内取值即可,此时cos(kixc-ωitc-2Nπ+θi)≥ 0,即cos(kix-ωit+θi)≥ 0,从而η2(x,t)≥ 0,这样波列群η1(x,t)和波列群η2(x,t)在叠加形成波形η(x,t)时就能保持始终有M-M1个波列为正幅度波,由此可以使得波能量在此正向聚焦,使得ηi(xc,tc)为正值,进而形成畸形波.同理可以推得其他情况下随机相位θi的取值范围.
同理,亦可以推知当kixc-ωitc<0时θi的调制取值范围.
2.2 电磁散射计算模型
在适合小尺寸粗糙面的微扰法(SPM)和适应大尺寸粗糙面的基尔霍夫近似法(KA)的基础上,我们对TSM进行修正,即结合微扰理论一阶近似来计算小尺度粗糙面散射系数,同时对大尺度粗糙面斜率分布做集平均运算进而实现粗糙海面的倾斜效应[15-20].后向散射系数的计算方法为(其中, x-z为其入射面):


其中,ki表示入射波波数;W(kx,ky)表示二维海谱(实际模拟中取JONSWAP谱模型);aHH,aVV表示HH极化、VV极化状态时其极化幅度.当入射波长λ已知时,其波数满足K ≤KL的空间随机面组成TSM中的大粗糙尺寸部分,其符合应用KA法近似条件,我们将这一部分用KA法来近似求解;而空间波数K≥Ks部分组成TSM中的小粗糙尺寸部分,其符合应用一阶微扰近似法的求解条件,我们用SPM法来计算.并且,小粗糙尺寸随机波面同时包括符合Bragg散射的空间波数K=KB=2kisinθi.这里使用(6)式来分辨大粗糙尺寸的截止波数KL.而计算小粗糙尺寸随机散射面过程中,由上所述可得,KS<KB=2kisinθi, kiθsmallcosθi≪ 1,其中边界参数阈值µ的取值取决于入射波数ki,由小粗糙尺寸的高度起伏方根可以求出KS,其表达式如下:

特别需要指出的是,(6)式中不等式左边部分

表示的是对应海面的平均曲率半径,由于实际海浪谱模型是多方向的,所以此处的Θ部分代表二维海浪方向谱的方向参数,然而考虑到下文中所研究的是一维畸形波仿真海面的单向散射特性(图5的实验结果),故在(10)式中给出的海浪谱函数(即S函数)为单变量函数,其只有频率参量而没有方向参量,故此处使其与海面10m风速u10的传播方向保持一致.本文实验中为了基于(2)式模拟畸形波的空间序列,我们令Θ取值为0,以此来表示(7)式中的方向谱取单一方向(即模拟一维的畸形波序列).
在具体分析畸形波散射过程中,由Bragg散射可知,海表面电磁波入射波数为k时,海面成像是通过电磁波与2k sin(θ)的组成波共振作用产生的,则由上述TSM散射理论可将畸形波任一点海表面高度划分为其波高与其波点相切的散射微面高度叠加,并且其任一散射微面的波高是Bragg波与该面元在此点斜率及长度的叠加,即

其中,

ki表示面元内Bragg散射短波波数;Shh=2Rq, Svv=2Rp,Svh=Shv=0,且Rq,Rp为Fresnel反射系数,
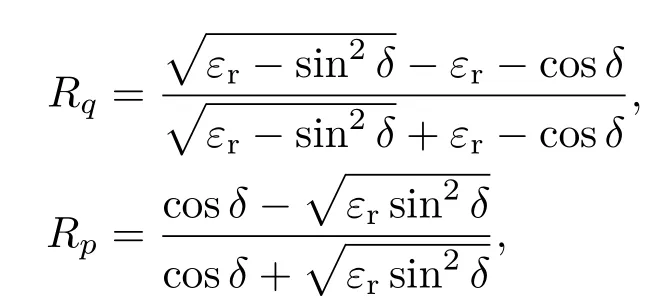
3 实验结果分析
3.1 仿真条件、畸形波的数值模拟及结果分析
本文采用JONSWAP谱[23]作为目标谱,JONSWAP谱是多个国家的学者基于北海“联合波浪计划”的大量实测资料而提出的风浪频谱,在模拟海浪波列方面其区别于其他海浪谱或者其他数学方法最大的优点在于引进谱升高因子γ来描述风浪的成长状态,后经过学者发展(进一步提出谱尖度因子P),使其可以由风浪的表观量有效波高H1/3和有效周期T1/3表示,从而使得JONSWAP谱更符合海浪成长规律,可以表征不同成长阶段的海浪.此外,叠加法符合海浪生成原理,就海浪波动原理而言,其更符合波群相互叠加的海洋现象及波浪生成规律,因此本文采用JONSWAP谱结合线性叠加法来进行海面建模符合物理海洋原理,且这一方法就实际操作而言,其比较容易验证波浪模拟效果.通过与目标海浪谱进行波浪谱谱形拟合(图3)及波浪的统计特性(图2中波高的超值累积概率分布)两组实验,证明此方法模拟精度较高. JONSWAP谱表达式如下:

其中,r,σ分别为峰升高因子和峰形参数;Emax表示谱峰值,且满足关系;当ω≤ω0时,σ=0.07,而当ω>ω0时,σ=0.09;a为无因次常数,且;为无因次峰频率,且此时(1)式中的ai即为JONSWAP谱形式.据此我们可以模拟距离空间位置x=0处畸形波的时间序列,如图1所示;同理我们可以模拟时间t=0时刻的畸形波空间序列,如图4结果所示.实验选取水深d=40 m,谱升高因子γ=3.3,有效波高hs=5m,谱峰周期为12 s,其组成波数M=100,调制波数取80,谱频范围(0,3.3),当时间tc=200时畸形波时间序列模拟结果如图1.
根据国际上对畸形波的普遍定义(Sand& K linting),畸形波波高Hj与其背景波的波高关系应满足条件:a1=Hj/HS≥2,a2=Hj/Hj-1≥2,a3=Hj/Hj+1≥2,a4=ηj/Hj≥0.65.其中a1,a2,a3和a4为畸形波特征参数;ηj为畸形波波峰高度(相对于水平线);Hj-1,Hj+1分别表示模拟序列中紧挨着畸形波前后的两个波波高.参数的参考分别基于上、下跨零法将畸形波特征参数时历记录,其图1中模拟中存在极值波的波浪特征参数统计列于表1.

图1 基于相位调制法的畸形波时间序列模拟结果Fig.1.Time series p lots for sim ulated freak waves with m od ified phase m odu lation method.

表1 上、下跨零法记录的畸形波特征参数值Tab le 1.The characteristic param eters of freak waves based on zero-crossing counting method.
同时,Rayleigh分布与模拟波高分布的对比结果、目标谱JONSWAP谱与波浪时历谱的比较结果分别如图2和图3所示.

图2 Rayleigh分布与模拟波浪的波高超值累积概率分布的对比结果Fig.2.Com parison of the exceedance p robability of wave height for the sim u lation with Rayleigh d istribution.
对比图2结果可知,畸形波仿真波列其超值累积概率分布在很大程度上与Rayleigh分布保持一致;图3则说明本文采用的调制方法在模拟畸形波波浪序列时比较契合原目标谱JONSWAP谱的频谱结构,谱峰周期也基本相同.上述参数对比分析结果(图1,表1)和模拟畸形波波浪谱的分析对比试验(图2,图3)充分说明了该调制方法的有效性.同时,经计算图1中有效波高hs=4.97 m,其与有效波高输入条件5m的相对误差为0.6%,在误差允许范围之内;此外其有效周期、谱峰周期等各参数都在误差范围内,其符合交通部的《波浪模拟试验规程》中各项参数的规定,并且其所有特征参数满足畸形波定义,初步证明了本调制方法的合理性.

图3 目标海浪谱JONSWAP谱与模拟海浪谱的对比结果Fig.3.Com parison of the sim u lated wave spectrum with the target spectrum.
3.2 电磁散射计算结果及分析
基于3.1节畸形波时间序列模拟过程时的初始条件,畸形波空间仿真序列及其背景波的空间序列模拟结果如图4.
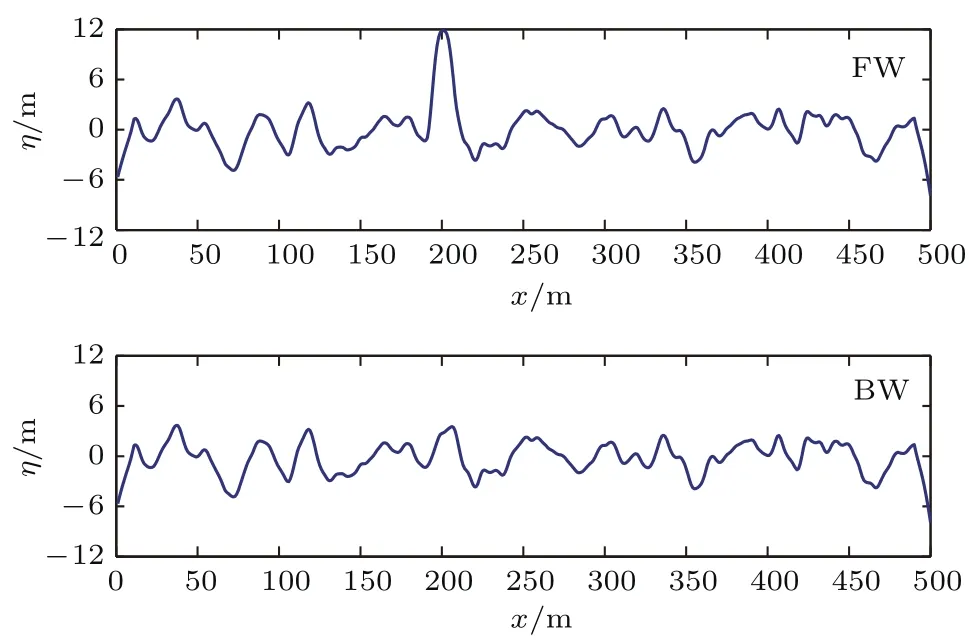
图4 相位调制法模拟的畸形波空间序列(FW)及其背景波序列(BW)Fig.4.Space series p lots for sim u lated freak waves (FW)with m od ified phase m odu lation method and background waves(BW).
考虑到进行电磁散射计算方法中近似算法的便捷性和数值方法的精确性,我们首先对二者进行误差分析.选取数值方法中的时域有限差分法(FDTD)进行分析.FDTD方法直接针对Maxwell旋度方程进行中心差分离散后得到一组差分方程,以TM波为例,则FDTD差分公式为[24]
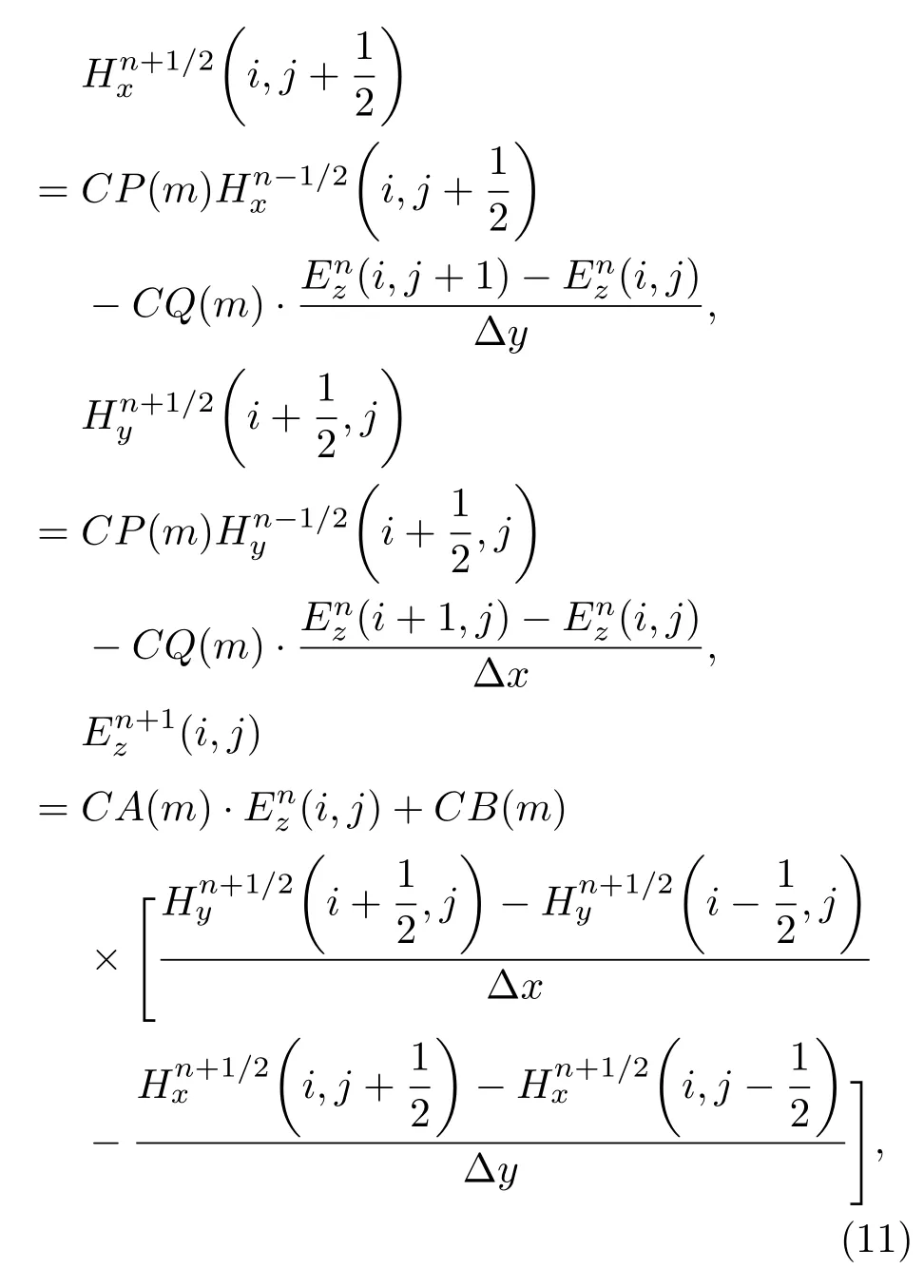
其中,m取值与左端场分量节点的空间位置相同;而CA(m),CB(m),CP(m),CQ(m)已知[24],其TE波的FDTD差分公式由TM,TE波二者对偶关系求得.鉴于FDTD计算中限于固定区域运算,在具体粗糙表面散射计算中,FDTD截断边界处需要有吸收边界,此处取单轴各项异性完全匹配层(UPML)吸收边界,则各向异性介质Maxwell旋度方程为(TM波、无源):

对上述公式进行中心差分近似则得到UPML的FDTD表达式,在其计算达到稳态后,去输出边界上相位、幅值,由等效原理利用时谐场外推公式得远区散射场如下:
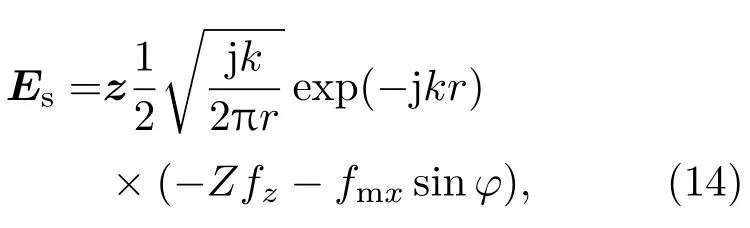

基于上述实验数据,从相对平均偏差和均方根偏差两个角度来衡量TSM法与FDTD法的计算误差.相对平均偏差和均方根偏差的表达式分别如下:

其中,R1,R2分别表示TSM,FDTD的散射系数.经计算得出δ1=3.8%,δ2=4.6%,二者均小于5%,在误差的允许范围之内.由于数值方法直接对Maxwell微分或者积分方程进行数值求解,其具有适用范围广、计算精度高的优点,而近似方法限于建模中物理近似的原因,其具有一定的适用范围.但在上述误差允许范围内,考虑到近似方法的简便性,特别是针对粗糙面掠入射散射计算而言,其散射系数的计算受到计算机内存和时间的限制,因此基于计算效率的考虑,本文采用近似方法的TSM法进行畸形波散射特性与识别标识的研究.

图5 TSM法和FDTD法计算畸形波FW的NRCS对比结果Fig.5.NRCS d iscrepancy of freak waves between TSM method and FDTD method.
在进行一维随机粗糙海面的电磁散射特性研究时,我们取实际数据风速u10为14 m/s,入射角为89.3512°,雷达工作频率为1.2 GHz,极化方式为HH极化,相对方位角为45°,风区为10 km,海表面的介电常数为(48.3,34.9)[18].在此条件下,计算图4畸形波空间序列及其背景波空间序列的电磁散射系数,结果如图6所示.

图6 畸形波FW及其BW的NRCS对比结果Fig.6.NRCS d iscrepancy between background waves (BW)and freak waves(FW).
图6所示为在HH极化条件下畸形波空间序列与其背景波空间序列的电磁散射特性对比,经分析可知,畸形波的后向散射系数在半波长一个周期范围内随着空间距离变化呈周期性改变,其散射特性很大程度上与背景波的散射特性相符,在对比结果中不含畸形波的背景波的NRCS在波峰处达到最大,波谷最小,同一空间位置的畸形波的NRCS值要偏小,其在200m处出现最小值-47.2123 dB,同时这也是图4中畸形波出现的空间位置,并且畸形波的最大波高位置(200m)处散射系数值比同一位置背景波散射系数小得多.这在原理上可以解释为:畸形波作为极端波现象,其底角与水平背景波夹角较大(如图4所示),而本文选取的雷达入射波接近掠入射状态(入射角为89.3512°),其突然产生的畸形波改变了原入射角大小,在入射光线不变的前提下,入射平面却由原来的水平海面改变为沿着畸形波斜角向上的平面,因此其入射波面的法向光线由原来的垂直于水平面变为垂直于畸形波边线平面,其入射角也由掠入射状态变为斜入射状态,进而致使入射到畸形波的反射光线与入射到背景波海面的反射光线的水平分矢量异向,其二者的散射波逆向叠加,使其中相位相反并且波长振幅满足一定条件的波的部分能量抵消,从而导致散射系数降低.此外,对比图4和图6还能发现,不论是背景波还是畸形波,在随机海浪一维空间序列中出现极值波的位置,其电磁散射系数呈现明显的非平滑过渡不稳定性.这是由于我们在使用TSM法计算海面后向散射系数时人为地把海面分解为大粗糙尺度的重力波和小粗糙尺度的张力波造成的.而实际上海面是相对均匀平滑过渡的,这也从另一个角度说明TSM法并不能充分适应随机粗糙海面的电磁散射计算,其过渡临界面处理还有待修正.在图4和图5出现极值波的前后,畸形波与其背景波的电磁散射系数出现了小范围剧烈变化现象,其原因可能是由于电磁散射计算时我们所采用入射角为89.3512°,但TSM模型中并未充分考虑极值波之间的散射遮挡效应所造成的,这有待进一步验证、改善.
基于以上研究结论,我们分析了风速从6-20 m/s条件下畸形波仿真空间序列的特征参数及其与背景波的电磁散射系数差值,实验结果列于表2.由实验结果分析,当风速为14 m/s时,特征参数a1,a2,a3和a4开始同时满足畸形波生成的判定条件,且此时畸形波与其背景波的NRCS差值是-11.8 dB,随着风速变大,其特征参数稳定满足畸形波判定条件,此时NRCS也逐渐变大.以上结论说明,NRCS差值可以作为畸形波判断及研究的一个特征参数,并且其标识阈值是-11.8 dB.

表2 不同风速下畸形波特征参数表(其中D表示畸形波及其背景波波列的NRCS差值)Table 2.The characteristic param eters of freak waves under the different wind velocities.
在上述研究结果的基础上,本文还就VV/HH极化条件下掠入射状态入射角为89.3512°时畸形波散射系数随入射频率改变的变化规律(图7), VV/HH极化下L波段入射频率1.2 GHz时畸形波后向散射系数随入射角改变的变化规律展开研究(图8).计算中取模拟序列中畸形波及紧挨着畸形波前后两个波作为波段对象.

图7 VV/HH极化下入射角89.3512°时畸形波后向散射系数随入射频率的变化Fig.7.E lectrom agnetic scattering characteristics of freak waveswith d iff erent incident frequency of polarization VV/HH and incident angle is 89.3512°.
如图7所示,掠入射状态下,随着入射频率增大,畸形波的后向散射系数不断增大但增大程度不断减小,其满足粗糙面散射理论.由图8结果可知,当入射频率一定、处在中小尺度的入射角度条件下, HH和VV两种极化条件下畸形波的后向散射系数计算结果较为相似,而随着入射角的增大,后向散射系数不断减小,且呈现极度下降的趋势.这是由于当擦地角逐渐变小时,雷达发出电磁波趋于逐渐接近平行海面的角度与海面相接触所致,此时后向散射系数较低.此外,还可以发现,两组实验数据中,VV极化方式下的畸形波的后向散射系数普遍高于HH极化下的后向散射系数.由于交叉极化情况下一般返回信号较弱,暂不进行研究,然而以上分析仅仅是理想状况下的固定海况条件下的理论结果,实际情况中还应该考虑实际风驱粗糙海面的泡沫(飞沫、气泡)等粒子对畸形波海面电磁散射的影响.

图8 VV/HH极化下1.2 GHz入射频率时畸形波后向散射系数随入射角改的变化Fig.8.E lectrom agnetic scattering characteristics of freak waves with different incident angle of polarization VV/HH and incident frequency is 1.2 GHz.
4 结 论
本文充分考虑了实际工程应用中弱非线性的Longuet-Higgins模型在模拟强非线性畸形波海面时所存在的问题,采用对随机相位修正的方法来模拟一维畸形波时间、空间波面,经过与Rayleigh分布的波高超值累积概率分布和目标海浪谱JONSWAP谱形对比,从而证明了该方法的有效性:该方法能实现畸形波的定时定点生成,并且其波形既能保持目标谱的频谱结构,又能较大程度地满足波浪序列的统计特性,其同时也满足初相位在(0 ,2π)范围内随机分布的要求.随后,本文针对FDTD法及TSM法的散射结果数据误差分析结果,基于计算效率的考虑,采用TSM模型研究了不同极化方式、不同入射角度、不同入射频率下畸形波及其背景波的电磁散射特性.实验结果表明,畸形波的NRCS要比背景波的NRCS值小很多.因此,考虑到实际的工程应用中特征参数a1,a2,a3和a4计算观测的复杂性,而NRCS差值却能够从SAR图像中间接计算得到,我们可以把畸形波与背景波的NRCS差值作为畸形波判断识别的一个特征参数.基于表2中的数据分析我们可以得出结论:当SAR图像中NRCS差值小于等于-11.8 dB时,即认为产生畸形波,并且在SAR图像上其产生畸形波的位置要相比其他位置更灰暗,这在实际的工程应用中为畸形波的判断识别提供了一定的参考依据.
[1]Kharif C,Pelinovsky E,Slunyaev A 2009 Rogue Waves in the O cean(Berlin:Deb lik)
[2]Didenku lova I I,Slunyaev A V,Pelinovsky E N,et al. 2006 Natura lHazards and Earth System Sciences 6 1007
[3]Kharif C,Pelinovsky E 2003 Europ.J.M ech.22 603
[4]K im N,K im C H 2003 In t.J.Off shore and Polar Engineering 13 38
[5]Pei Y G,Zhang N C,Zhang Y Q 2007 Acta Oceanol. Sin.29 172(in Chinese)[裴玉国,张宁川,张运秋2007海洋学报29 172]
[6]Pei Y G,Zhang N C,Zhang Y Q 2007 China Ocean Engineer.21 515
[7]Huang G X 2002 Ph.D.D issertation(Dalian:Dalian University of Technology)(in Chinese)[黄国兴2002博士学位论文(大连:大连理工大学)]
[8]Liu X X,Zhang N C,Pei Y G,Zhang Y Q 2007 Num erical Sim u lation of Freak W aves in Three-D im ensiona l Wave Field(Beijing:China Ocean Press)pp908-914(in Chinese)[刘晓霞,张宁川,裴玉国,张运秋2007中国环境资源与水利水电工程(北京:海洋出版社)第908-914页]
[9]Zhao X Z,Sun Z C,Liang S X 2009 China Ocean Engineer.23 429
[10]Liu Z Q,Zhang N C,Yu Y X 2011 Acta Oceanol.Sin. 30 19
[11]Zhang Y Q,Zhang N C 2007 Acta Oceanol.Sin.26 116
[12]Zhang Y Q,Zhang N C,Pei Y G 2007 China Ocean Engineer.21 207
[13]Onorato M,Osborne A R,Serio M 2004 Phys.Rev.E 70 67302
[14]Longuet-Higgins M S 1952 J.M arine Res.11 245
[15]W u G K,JiG R,Ji T T,Ren H X 2014 Acta Phys.Sin. 63 134203(in Chinese)[吴庚坤,姬光荣,姬婷婷,任红霞2014物理学报63 134203]
[16]Guo L X,W ang Y H,W u Z S 2005 Acta Phys.Sin.54 5130(in Chinese)[郭立新,王运华,吴振森2005物理学报54 5130]
[17]Yang J L,Guo L X,W an JW 2007 Acta Phys.Sin.56 2106(in Chinese)[杨俊岭,郭立新,万建伟2007物理学报56 2106]
[18]U laby F 1982M icrowave Rem o te Sensing(Vol.2)(London:Addison-W esbey Pub lishing)
[19]W ang Y H,Guo L X,W u Z S 2006 Acta Phys.Sin.55 209(in Chinese)[王运华,郭立新,吴振森2006物理学报55 209]
[20]Zhang Y D 2004 Ph.D.D issertation(X i’an:X id ian University)(in Chinese)[张延冬2004博士学位论文(西安:西安电子科技大学)]
[21]V lad im ir K,Daniele H 2003 J.Geophys.Res.108 8054
[22]X ie T,He C,W illiam P,K uang H L 2010 Chin.Phys. B 19 024101
[23]Xu D L,Yu D Y 2001 Theory of Random Waves(Beijing:Higher Education Press)pp200-204(in Chinese) [徐德伦,于定勇2001随机海浪理论(北京:高等教育出版社)第200-215页]
[24]Ge D B,Yan Y B 2005 Finite-D iff erence Time-Dom ain M ethod for E lectrom agnetic W aves(X i’an:X idian University Press)(in Chinese)[葛德彪,闫玉波2005电磁波时域有限差分方法(西安:西安电子科技大学出版社)]
(Received 30 Decem ber 2016;revised manuscript received 25 April 2017)
Electromagnetic scattering characteristics analysis of freak waves and characteristics identification∗
Wu Geng-Kun Song Jin-Bao Fan Wei†
(O cean College,Zhejiang University,Zhoushan 316000,China)
Based on the Longuet-Higgins wavemodel theory,a modified phasemodulation method of simulating freak waves is im proved in this paper.Themethod can generate freak waves at assigned time and p lace,and their waveform s can not only m aintain the frequency spectrum structure of the target spectrum and also satisfy the wave series statistics to a great extent.Then,the electromagnetic backscatteringmodel of freak and background wave is estab lished by the finite difference time dom ain method and the two-scalemethod.A fter averaging relative deviation and analyzing the error of the rootmean square deviation within themeasurement uncertainties,considering the com putational efficiency,we use the two-scalemodelmethod to calculate the electrom agnetic scattering coefficient of freak wave.Num erical results show that the norm alized radar cross section(NRCS)of freak wave ismuch sm aller than that of background wave.On the other hand,we analyze the electromagnetic scattering p roperties of freak waves under the different polarization modes, incident angles and incident frequencies.We find that in the condition of grazing incidence,the backscatter coefficient of freak wave increases with the increase of the incident frequency,but the increase am p litude is reduced,which m eets the rough surface scattering theory.W hen the incident frequency is fixed and the incident angle is small,the backscatter coefficient calculation results of freak wave are sim ilar under the condition of different polarizations VV’s and HH’s, but the backscatter coefficient of freak wave decreases obviously with the increase of incident angle,which is caused by the radar electromagnetic wave that is parallel to the sea surface and contacts it gradually.In addition,we find that the backscatter coefficient calcu lation result of freak waves under the VV polarization ismuch higher than under HH polarization from the two groups of experimental figures.According to the result of datum analysis,a conclusion is drawn that we can determ ine where the freak wave is when the NRCS difference of synthetic aperture radar(SAR) im age is sm aller than-11.8 dB.In the practical engineering app lication,the characteristic param eters are diffi cult to observe,while the difference in electromagnetic scattering coefficient between freak wave and background wave can be calculated from the SAR im age of sea surface.This conclusion provides a reference standard for predicting the freak waves in engineering app lication,through which we can calcu late the characteristic param eters of freak wave,determ ine its position,and study the electromagnetic scattering characteristics under the different polarization modes,incident angles and incident frequencies in future researches.
freak waves,phasemodulation,electromagnetic backscattering,indicator
PACS:43.30.Hw,13.40.Ks,42.68.M j DO I:10.7498/aps.66.134302
∗国家自然科学基金(批准号:41576013)、国家高技术研究发展计划(批准号:2013AA 122803)和国家重点研发计划(批准号: 2016YFC 1401404)资助的课题.
†通信作者.E-m ail:fanwei@zju.edu.cn
PACS:43.30.Hw,13.40.Ks,42.68.M j DO I:10.7498/aps.66.134302
*Pro ject supported by the National Natu ral Science Foundation of China(G rant No.41576013),the National H igh Technology Research and Developm ent Program of China(G rant No.2013AA 122803),and the National Key R&D Plan,China (G rant No.2016YFC1401404).
†Corresponding author.E-m ail:fanwei@zju.edu.cn

