地磁场实验中测量装置的改进

毛忠泉，聂 丹

(华南理工大学 物理与光电学院，广东 广州 510640)

地磁场实验中测量装置的改进

毛忠泉，聂 丹

(华南理工大学 物理与光电学院，广东 广州 510640)

基于磁阻传感器的地磁场测量实验中,磁阻传感器芯片所在转盘的可调自由度较低，在测量地磁场总量和磁倾角时会出现较大误差，且操作较复杂. 为此把原装置的单环转盘改良为三环转盘，改进后的实验装置可以直接测量地磁场的大小和磁倾角，并有效地降低实验误差，同时能更直观地展示地磁场矢量和地磁子午面之间的几何位置关系.

地磁场；磁倾角；磁阻；子午面；单环转盘；三环转盘

地磁场是地球及其周围空间存在的天然磁场. 地磁场的分布类似于磁偶极子所形成的磁场分布，地磁的南极和北极分别对应于地理的北极和南极，磁轴与地球自转轴夹角约为11.5°. 地磁场的强度非常小，约为10-5T量级. 地磁场在军事、航天、航海和地震预测等科研领域中有重要的应用. 地磁场测量方法有多种，如光磁共振法、磁聚焦法、磁旋光成像法、正切电流计法和磁阻传感器测量方法等[1-6]，其中磁阻传感器测量方法的测量装置简单，操作简便，拓展性强，是目前大学物理实验教学中最常用测量方法[7-10]. 但是，实验教学仪器主要采用单环转盘结构，在直接测量地磁场总强度和磁倾角实验中容易引入较大误差，也不利于学生观察地磁子午面. 本文介绍一种改进该实验装置的简单方法，通过把原来的单环转盘改进为三环转盘后，可直接测量地磁场的大小和磁倾角，并能有效地降低实验误差.

1 实验原理

地磁场矢量B在水平地面上的分量为B∥，指向地心的垂直分量为B⊥，B∥与B所在平面为地磁子午面，B∥与B的夹角为磁倾角β. 在大学物理实验中要求测量出B和β. 磁阻传感器测量方法是利用磁阻电桥芯片来测量磁场的大小和方向. 磁阻电桥的4个桥臂为波莫合金薄膜制备的各向异性磁电阻[7]，其输出电压Uout与芯片平面的磁场大小B的关系为

Uout=U0+KBcosθ,

(1)

其中，U0是与磁场无关的电压输出，K为电桥的灵敏度，θ为电桥芯片的引脚方向与磁场方向的夹角. 由(1)式可见，当电桥芯片的引脚方向与磁场方向平行时，输出电压最大，设为Umax；当电桥芯片的引脚方向与磁场方向反平行时，输出电压最小，设为Umin. 于是，磁场的大小可表示成：

B=(Umax-Umin)/2K,

(2)

由此可见，只要在水平地面或地磁子午面转动电桥芯片，分别测出Umax和Umin，即可得到B∥或B的值，通过测量在地磁子午面中转过的角度即可得到β.

2 实验装置及改进方案

2.1 现有实验装置及实验方案

目前大部分高校的地磁场实验装置为上海复旦天欣科教仪器有限公司的磁阻效应地磁场测试仪，其装备了HMC1021Z磁阻电桥芯片. 测试仪由亥姆赫兹线圈和固定了芯片的转盘构成，其中转盘只有水平和垂直2种位置，可调自由度较低，如图1(a)～(b)所示. 测量磁场前，需先通过亥姆赫兹线圈测出芯片的灵敏度K[7-8]. 地磁场的测量则主要有3种方案：

1)在水平面转动转盘，测出Umax和Umin，通过(2)式求出水平分量B∥[图1(a)]. 调整转盘为铅直，同时把芯片引脚方向调节到铅直，测出垂直分量B⊥.B和β由B⊥与B∥合成求出[7].

2)建立直角坐标系，分别测出Bx，By，Bz，最后通过矢量合成求出B和β[9].

3)把转盘调整成铅直，并转动转盘使芯片引脚的方向水平；然后在水平面上转动整个实验仪，直到输出电压为最大(或最小)，此时转盘平面便是地磁子午面，最后在地磁子午面上转动转盘，电压输出最大值时，引脚方向便是地磁场的方向[图1(b)],通过(2)式可求得其大小[7-8].

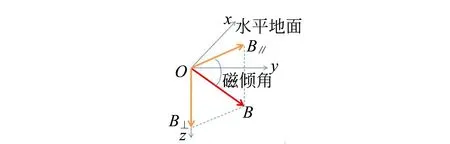
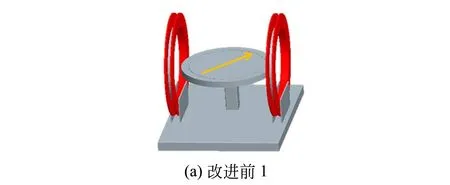
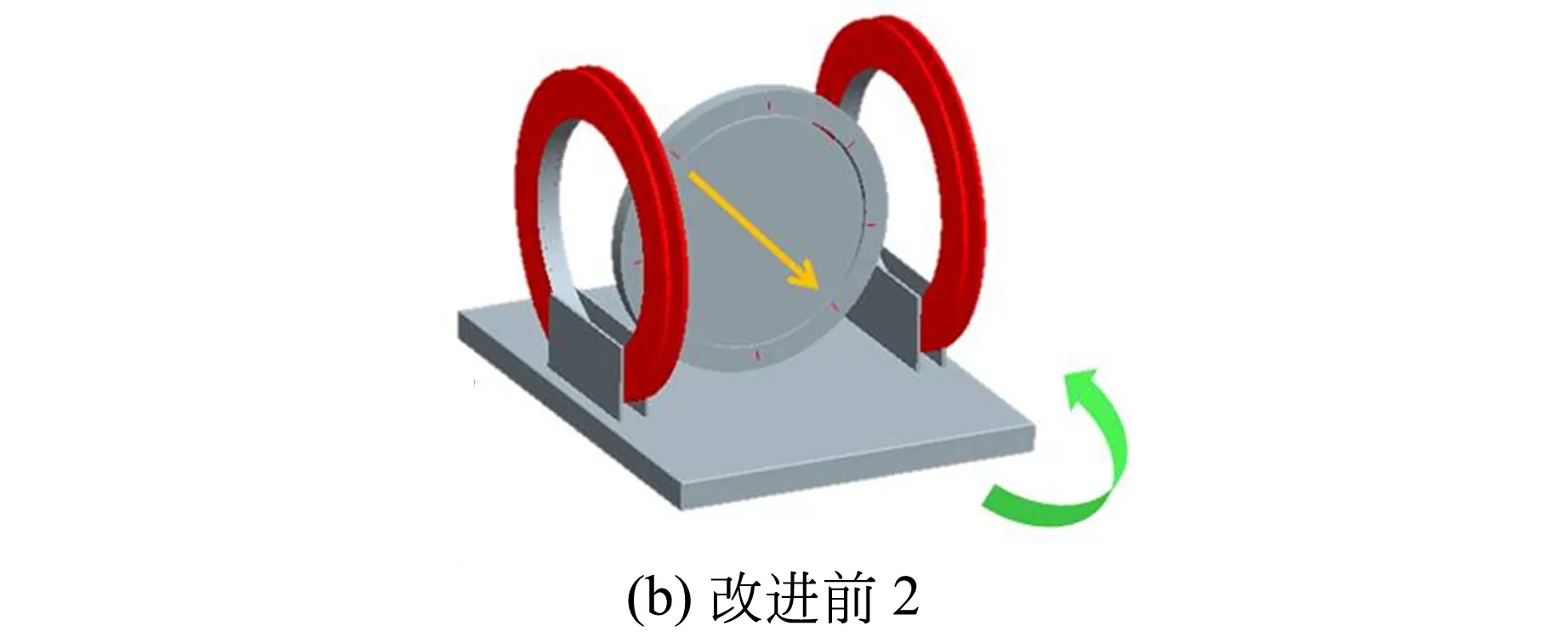
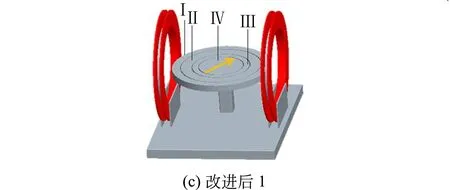
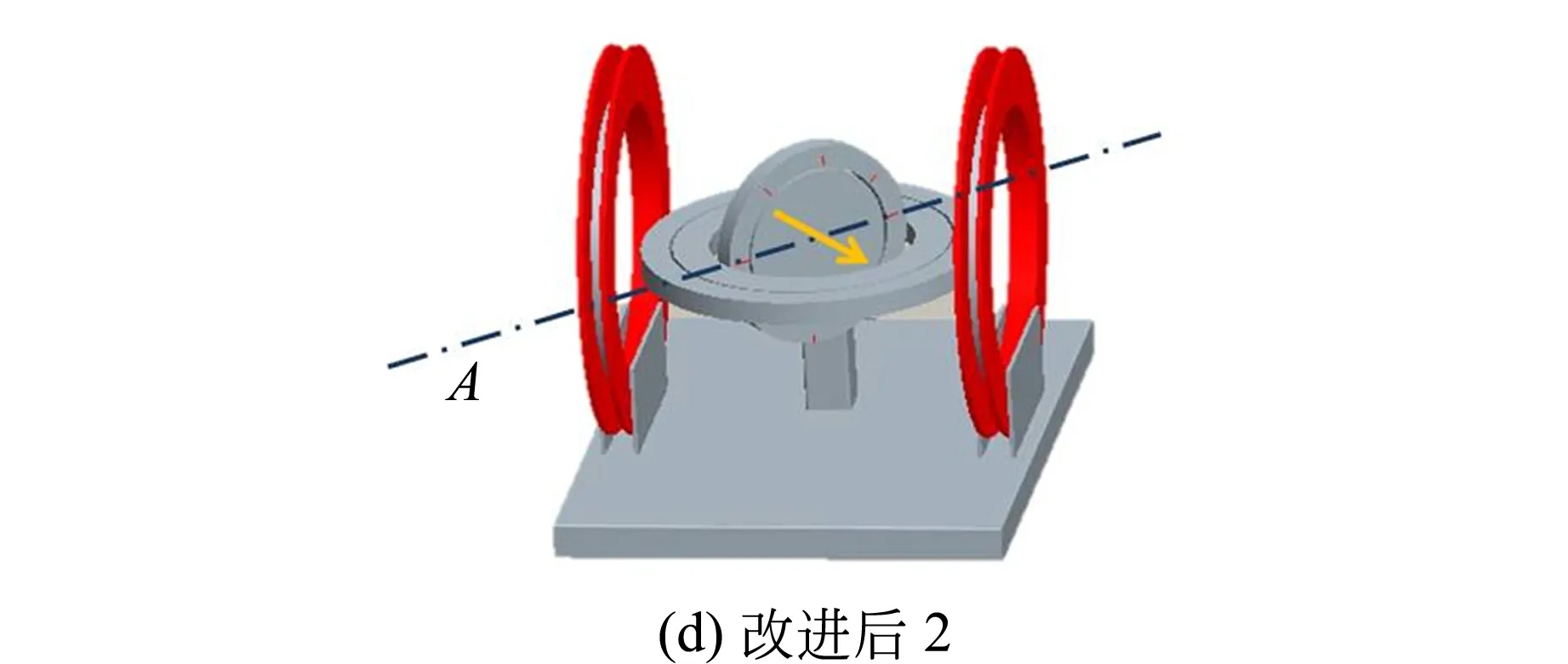
图1 改进前后的地磁场测量仪示意图(黄色箭头代表引脚方向)

前2种方案的缺点是间接测量地磁场总强度，不直接涉及地磁子午面，导致学生不理解地磁子午面. 第3种方案虽然引入了子午面，但是由于不能保证实验桌面处处水平，转动整个实验装置引入很大的误差，影响实验数据的准确度.

2.2 改进实验装置及实验方案

为了克服上述问题，本文提出改进方案，只需要对转盘做简单地改良即可. 如图1(c)所示，把原来的单环转盘结构改成三环转盘结构. 钢环I起支撑作用，固定在支架上；钢环Ⅱ可在钢环Ⅰ的平面上转动；钢环Ⅲ为刻度盘，通过转轴A与钢环Ⅱ相连，可绕转轴转动，如图1(d)所示；HMC1021Z芯片固定在中心盘Ⅳ的中心，中心盘Ⅳ可在钢环Ⅲ的平面内转动. 各钢环、中心盘间通过锁止螺钉和转动旋钮调节相对转动.

改进后的实验装置可操作性更强，可胜任更多的测试功能. 以下是常用的实验测量方案：

1)测量灵敏度K. 调整钢环Ⅰ，Ⅱ，Ⅲ和中心盘在同一个水平面内，转动中心盘使芯片引脚与转轴A重合；转动钢环Ⅱ使芯片引脚与亥姆赫兹线圈中心轴重合. 测出输出电压与励磁电流的关系，从而计算出K.

2)测量水平分量B∥. 在水平面内转动钢环Ⅱ[从而带动钢环Ⅲ和中心盘，如图1(c)所示]，测量出输出电压的最值，从而计算出B∥.

3)测量总强度B和磁倾角β. 在水平面内找到输出电压的最大值后，锁紧钢环Ⅰ和Ⅱ之间的螺钉，调节钢环Ⅲ(带动中心盘)与水平面垂直. 此时，钢环Ⅲ与中心盘所在平面为地磁子午面，如图1(d)所示. 在地磁子午面上转动中心盘到电压输出的最大值位置，此时引脚所指方向为地磁场矢量的方向，从钢环Ⅲ的刻度上可直接读出磁倾角β. 根据输出电压的最值可算出B.

4)测量垂直分量B⊥. 只需要调节中心盘使芯片引脚沿铅直方向，测出相应的输出电压即可算出B⊥.

2.3 测试结果

用同一块K=52.6 V/T的HMC1021Z芯片分别安装在改进前和改进后的实验仪中，测量了华南理工大学五山校区实验楼的地磁场的水平分量和总量. 图2为30次等精度测量的结果. 由图2可见，对于水平分量，改进前和改进后的测试结果基本一致. 但是，对于总磁场，改进前测量的数据离散度较高，B=(0.512±0.030)×10-4T；而改进后测量的数据离散度明显减小，B=(0.467±0.009)×10-4T. 改进后的实验数据与广州地磁台所测数据更吻合(0.452×10-4T)[11]，而改进前的测量结果则误差较大，这很可能是由于实验时在非水平的桌面上转动仪器造成的系统误差. 类似的情况同样发生在测量磁倾角的实验中，此处不再赘述.

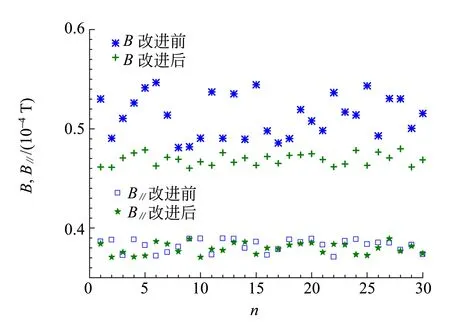
图2 改进前和改进后的实验装置测量地磁场的结果

3 结 论

综上所述，通过把地磁场测量装置的单环转盘改进为三环转盘后，可以直接测量地磁场的大小和磁倾角. 通过对比测试，发现改进后的仪器可以有效地降低实验的系统误差. 同时，由于增加了转盘的自由度，使得仪器在操作上的拓展性和灵活性更强，有利于在实验过程中加深学生对地磁子午面的理解.

[1] 吴奕初，胡占成，刘海林，等． 光磁共振实验测量地磁场方法的探究[J]． 物理实验，2016，36(4):1-6.

[2] 王玉清，杨德甫,刘艳峰，等． 利用磁聚焦法测量地磁场的研究[J]. 大学物理， 2009，28(7):36-38．

[3] 李小俊，白晋涛，李永安，等． 磁旋光成像地球磁场测量方法[J]． 自然科学进展，2007，17(9):1168-1173．

[4] 苏学军，牟青，曹彪，等． 电子自旋共振对地磁场的测量方法[J]． 实验室研究与探索， 2013，32(10):44-47．

[5] 王思慧,刘振宇,江洪健，等. 磁针磁矩的测量和耦合磁针的实验研究[J]． 物理实验，2016，36(3):19-23．

[6] 王国余,张欣,景亮. 新型磁阻传感器在地磁场测量中的应用[J]. 传感器技术,2002,21(10)：43-45.

[7] 周晓明. 大学物理实验[M]. 广州：华南理工大学出版社，2012：363-367.

[8] 魏奶萍. 磁阻传感器测量地磁场的实验数据处理[J]. 大学物理实验， 2016，29(3):115-117．

[9] 杨春振，崔泽轮. 基于新型磁阻传感器的地磁倾角测量[J]. 大学物理实验， 2012，4:3-5．

[10] 吴春姬，纪红，徐智博，等. 巨磁电阻效应实验仪[J]. 物理实验，2015，35(3):33-36.

[11] 罗玉芬，黎晓之，陆镜辉. 广州地磁台地磁场长期变化的分析研究[J]. 防灾技术高等专科学校学报，2005，7(4)：64-67.

[责任编辑：尹冬梅]

Improvement of the equipment in geomagnetic field measuring experiment

MAO Zhong-quan, NIE Dan

(Department of Physic, South China University of Technology, Guangzhou 510640, China)

In the geomagnetic field measuring experiment based on magnetic resistance sensor, the uncertainty in measuring the amplitude of the geomagnetic field and geomagnetic inclination was large due to the low freedom of the spin disc. Here a three-ring spin disc was designed to substitute the single-ring spin disc. In this way, the measuring error was reduced. At the same time, the improved equipment could help to demonstrate directly the relative position of different geomagnetic vectors and the geomagnetic meridian plane.

geomagnetic field; geomagnetic inclination; magnetic resistance; geomagnetic meridian plane; single-ring spin disc; three-ring spin disc

2017-01-18

国家自然科学基金(No.NSFC11304098)

毛忠泉(1980-)，男，广东化州人，华南理工大学物理与光电学院讲师，博士，从事纳米磁学方面研究.

O441.5

A

1005-4642(2017)07-0014-03