可逆矩阵的初等变换对其逆矩阵的影响

周慧倩

(洛阳师范学院 数学科学学院，河南 洛阳 471022)

可逆矩阵的初等变换对其逆矩阵的影响

周慧倩

(洛阳师范学院 数学科学学院，河南 洛阳 471022)

通过伴随矩阵和初等矩阵的理论，推导当可逆矩阵做初等变换时，其逆矩阵的变化规律．

可逆矩阵；逆矩阵；伴随矩阵；初等变换

0 引言

可逆矩阵是线性代数的重要内容，是解决科学研究以及生产实践中诸多问题的重要理论工具[1-3]，有必要对这部分内容做深入的探讨．与矩阵密切相关的是初等变换，那么当可逆矩阵做初等变换时，逆矩阵如何变化？这是一个有趣又有用的问题，讨论它并不复杂也不困难，但是很有意义．一方面这个结论很多地方会用到，到用时再去推导未免麻烦误事;另一方面通过这些讨论可以加深学生对相关知识的理解，促进知识的融会贯通，锻炼学生独立探索、深入思考问题、解决问题的能力．

1 伴随矩阵法

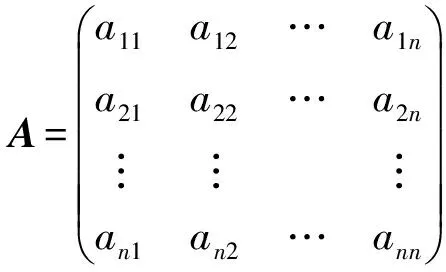
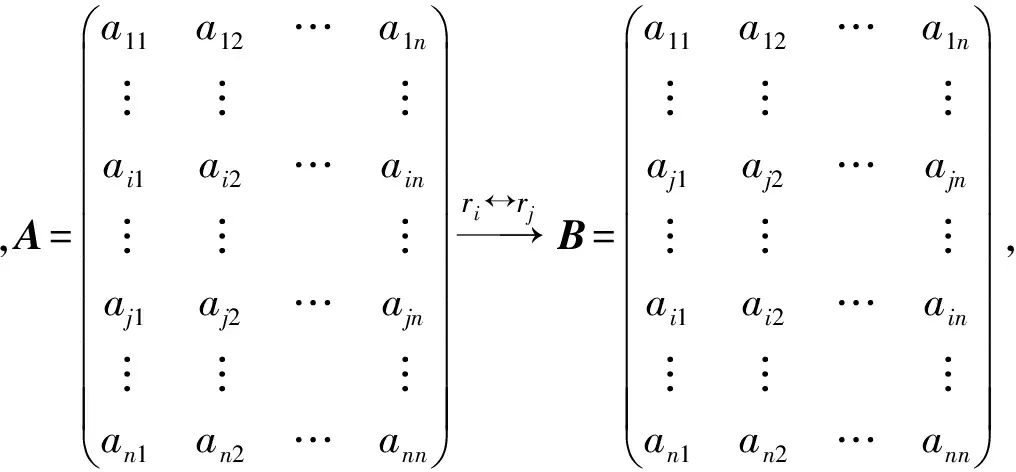
于是

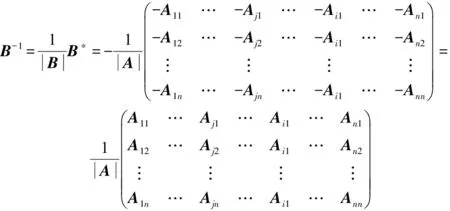
可见B-1可由A-1互换i，j列所得．

2)A的一行乘一非零数，

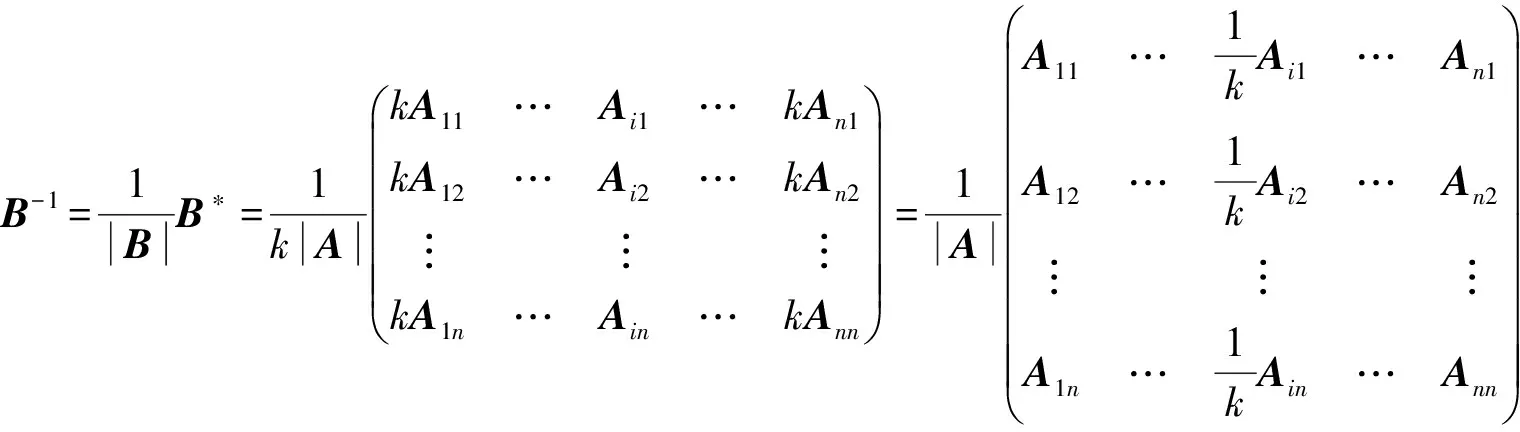
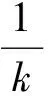
3)A的一行的倍数加到另一行，

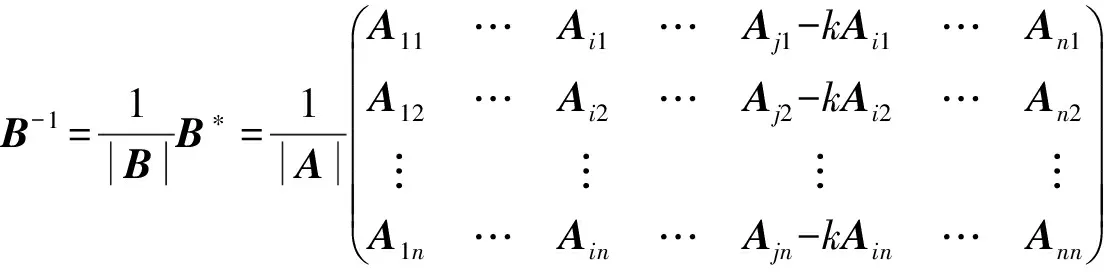
可见B-1可由A-1第i列的-k倍加到第j列所得．

2 初等变换法

根据初等变换与初等矩阵的关系，也可证明上面的结论．

设可逆n阶矩阵A经一次初等行变换化为B，则有初等矩阵Q,使B=QA,则B-1=(QA)-1=A-1Q-1.

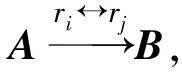
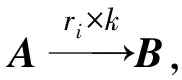
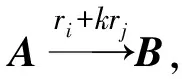
以上的讨论结果即定理1．

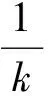
3 列变换的情形

对于三种列变换的讨论用上述两种方法类似进行，结论如下：

相应地有定理2．

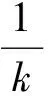
[1] 同济大学数学系.工程数学线性代数[M].5版.北京：高等教育出版社，2011:57-63.

[2] 谭军.矩形初等变换的一些性质及应用[J].郑州航空工业管理学院学报，2002(4)：71-73.

[3] 倪臣敏，孙逊.矩阵的初等变换在《线性代数》中的应用[J].四川教育学院学报，2008(7)：104-107.

[4] 王萼芳.高等代数[M].5版.北京：高等教育出版社，2013：177-192.

[5] 王天泽.线性代数[M].北京:科学出版社,2013:46-48.

ElementaryTransformationsofInvertibleMatrixonItsInverseMatrix

ZHOU Huiqian
(CollegeofMathematicsScience,LuoyangNormalUniversity,Luoyang471022,China)

By the theory of adjoint matrix and elementary matrix, the change rules of its inverse matrix are derived when elementary transformations are transformed to invertible matrix.

invertible matrix; inverse matrix; adjoint matrix; elementary transformation

2016-11-04

周慧倩(1981—)，女，河南延津人，洛阳师范学院数学科学学院讲师.

10.3969/j.issn.1007-0834.2017.02.012

G642.0;O151.21

：A

：1007-0834(2017)02-0052-03