应用新型Lanchester方程的非对称空战进程预测

张洋铭，陈云翔，蔡忠义，项华春

（空军工程大学装备管理与安全工程学院，西安 710051）

应用新型Lanchester方程的非对称空战进程预测

张洋铭，陈云翔，蔡忠义，项华春

（空军工程大学装备管理与安全工程学院，西安 710051）

针对未来空战中可能出现的非对称空战问题进行研究，在设定的非对称空战背景下构建新型Lanchester方程对问题进行建模分析，得到单一机种和多兵种非对称空战模型，并通过仿真试验验证了模型的有效性，对非对称空战指挥决策提供了一定的帮助。

新型Lanchester方程，非对称空战，进程预测

0 引言

现代战争中由于高技术武器装备的广泛应用以及战场环境的变幻莫测，交战某一方往往会呈现出非对称的作战优势，并借助该优势一举歼灭敌人取得战争胜利。美军在近几次高技术局部战争中，充分利用自身空中力量和信息力量的非对称优势势如破竹，赢得战场胜利。想要在未来空战中占据主动权，就必须对非对称空战态势进行深入研究。

兰彻斯特方程是一种能有效预测战争进程的军事运筹方法，它的经典模型已经成功应用于战斗建模、耗损预测、人口发展等诸多领域，如文献［1］利用兰彻斯特方程构建空中体系对抗模型，文献［2］利用兰彻斯特方程面开火模型建立现代海战损耗模型，文献［5］中利用兰彻斯特平方律解决空战对抗问题，这些文献都在兰彻斯特方程基础上进行了一定程度的改进，但是由文献［3］可知未来空中作战也将呈现非对称空战态势，同军种多兵种作战模式雏现，需要针对各类非对称因素进行特定研究，基于此，本文拟采用一种综合考量空战态势的新型兰彻斯特方程来研究非对称空战问题，建立非对称空战进程模型，并对未来非对称空战的主要决定性影响因素进行分析探讨。

1 非对称空战概述

非对称空战是指空战双方在不对等条件下，尤其是指空战双方使用不同类型作战力量（这里不仅包含空中格斗的战斗机，也包括双方进行防空作战的地面武器装备等）、不同类型战法或不对等的战场信息资源情况下进行的空战。非对称空战主要有两种类型：一种是以整体强势为基础，比如一方空中力量、防空力量、信息力量全面压制对方的非对称空战；另一种是整体弱势的一方以创造局部优势为基础，比如一方超视距攻击优势明显的非对称空战。

非对称空战既能够使强者更强，也能够使弱者在局部占优，既是强者的有利选择，更是弱者的最佳选择。在运用非对称空战战略时，不能盲目追求高精尖技术的运用，不能只与对手比较武器装备的战术技术性能优劣，而应该注重对传统作战手段和技术装备进行创新性应用，坚持高中低技术装备相结合、常规和非常规手段相结合，发挥多种作战手段的综合优势，以联合作战行动形成体系作战能力对对手作战体系中最具关键性、易损性和杠杆性的节点进行打击，最终赢得空战胜利。

本文在考虑空战双方非对称条件时，主要从作战力量和信息力量出发，以双方空战装备作战效能非对称、信息力量非对称和作战协同能力非对称等几个方面考虑，来研究非对称空战的进展情况。

2 兰彻斯特方程概述

兰彻斯特方程是著名的英国汽车工程师、流体力学家和运筹学家兰彻斯特在1914年提出的一种描述飞机运用和空战的战斗动力学方程，兰彻斯特方程能够有效预测战争进程和战斗损耗情况，对战术运用和兵力部署起到很好的指导作用。兰彻斯特方程最早主要有3种基本模型：直接开火模型、格斗模型和面开火模型，随着时间推移出现了游击战模型、自主开火模型、几何平均模型等，不同的战场态势需要用不同的模型解析，这里只介绍作为本文研究模型基础的直接开火模型和面开火模型。

2.1 兰彻斯特直接开火模型

兰彻斯特直接开火模型的主要假定是双方兵力完全暴露在对方视野或侦查范围中，在对方武器射程内进行连续战斗，一方的武器开火均匀分布在另一方的战斗单位上且命中即摧毁，一方的有效开火速率与另一方的兵力水平无关。在这样的假定下可以列出兰彻斯特直接开火模型的常微分方程为：

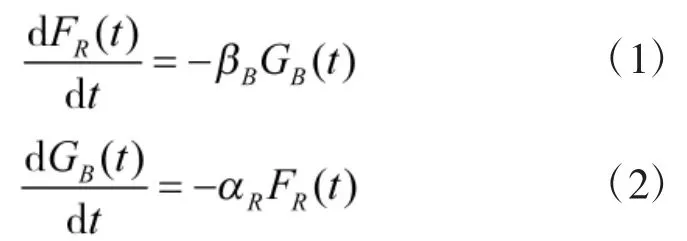
其中，FR（t）为红方在t时刻作战力量（可以表示为武器装备或战斗人员数量，也可以表示为作战力量指数），αR为红方对蓝方的损耗系数（战斗单位的平均作战效能值），GB（t）为蓝方在t时刻的作战力量，βB为蓝方对红方的损耗系数。根据直接开火模型的常微分方程可以得到双方作战力量的时间解为：

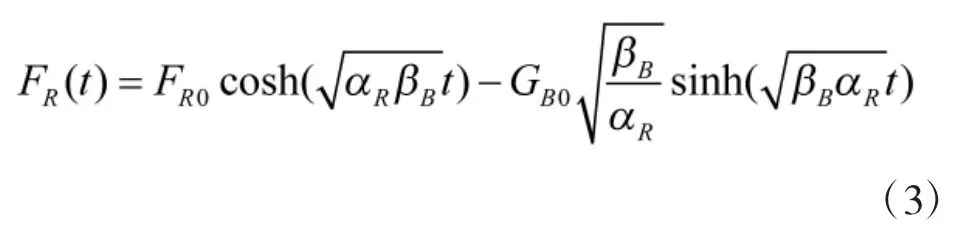
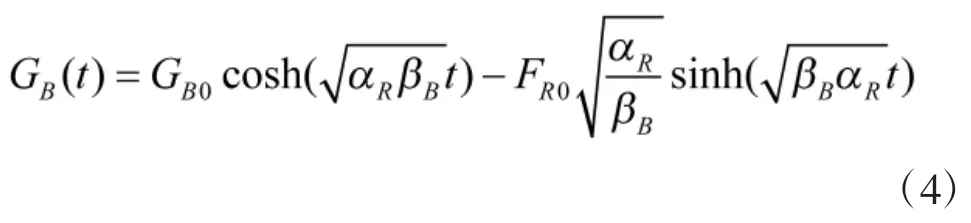
同时可以经过变换得到双方作战的取胜时间解：

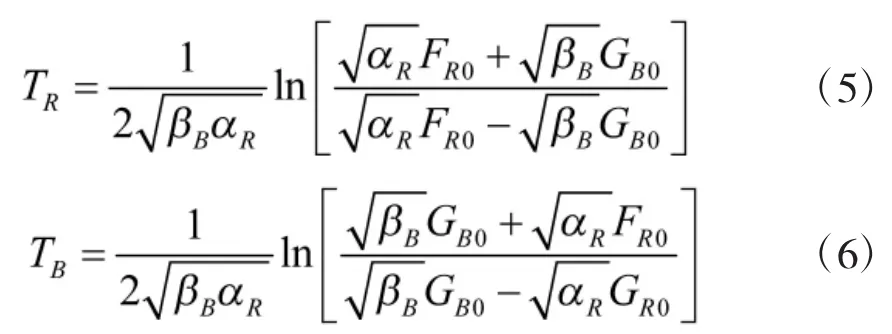
2.2 兰彻斯特面开火模型

兰彻斯特面开火模型的主要假定是双方进行连续战斗时一方完全暴露或信息透明，另一方信息未知或信息不全面，双方所有战斗力量分布在整个面上，每一方的损耗速率与双方作战力量的乘积成正比。在这样的假定下可列出兰彻斯特面开火模型的常微分方程为：

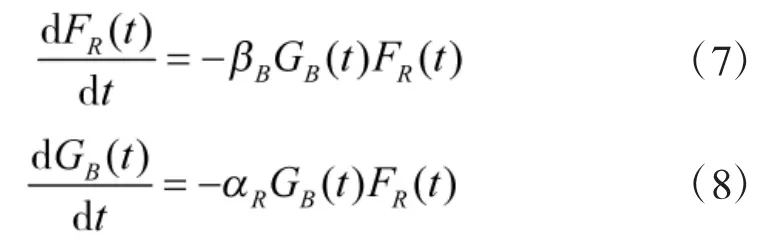
同样也可以得到其时间解：

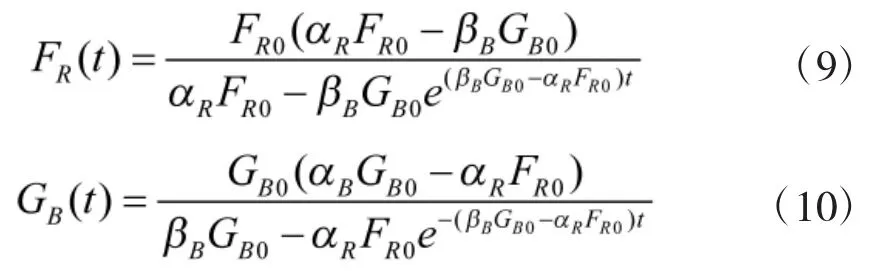
在兰彻斯特相应模型基础上可以针对特定作战背景对兰彻斯特方程进行改进，使之适应现代战争和未来战场的需求。接下来利用改进的兰彻斯特方程对非对称空战进程进行预测。

3 改进型兰彻斯特空战预测模型

3.1 非对称想定

针对前文中对非对称空战的描述，后面主要从空战中进行空空作战、空地作战和防空作战的战斗力量作战效能非对称、信息力量非对称和作战协同能力非对称几个方面，对非对称空战中的兰彻斯特模型进行建立。本文假设交战双方在开阔地域进行连续战斗，视空、地武器装备与操作人员为同一的整体，损耗即为消灭，不考虑累计毁伤；实际战斗过程中双方信息力量未知（即有可能出现面开火的情况），具有信息优势的作战力量对劣势力量为直接开火，处于信息劣势的作战力量为面开火；考虑实战中存在飞机等武器装备中非战斗减员的情况且双方兵力可以补充，在这一系列想定下进行模型建立。

3.2 单一机种非对称空战模型

在空战领域中，所谓“单一兵种”空战指的是双方单一型号机群交战，双方战机可以采用不同编队和不同战法进行作战；所谓“多兵种”空战指的是多种不同类型的空地武器装备协同交战，因此，构建单一机种非对称空战模型时只考虑单一型号的战机交战即可。假设F（Rt）、G（Bt）为红、蓝方在t时刻作战力量情况，LR、LB为红、蓝方兵力补充速率，δR、δB为红、蓝方非战斗损失率，μR、μB为红、蓝方直接开火的比例系数，αR、分别为直接开火、面开火时红方对蓝方的损耗系数，βB、分别为直接开火、面开火时蓝方对红方的损耗系数。这里对损耗系数的处理采用经典的损耗系数方程，可以认为损耗系数只与双方武器装备的发现概率 P（h）和击毁概率 P（k｜h）有关，即和求法类似，不再赘述。在此基础上构建单一兵种非对称空战的常微分方程如下：

3.3 多兵种非对称空战模型

实际空战中交战双方在开阔地域往往会出现空空交战、空地交战和防空作战相结合的立体化交战模式，这个时候就会有多个兵种参与到空战过程，比如歼击机部队、轰炸机部队、地空导弹部队、高炮部队等，每个参战兵种都会对对方相应兵种进行打击或干扰，这就需要对多兵种非对称空战情况进行考虑。假设FRi（t）、GBj（t）为红、蓝方各兵种在t时刻作战力量情况，LRi、LBj为红、蓝方各兵种作战力量补充速率，δRi、δBj为红、蓝方各兵种非战斗损失率，μRi、μBj分别为红、蓝方各兵种直接开火的比例系数，分别为直接开火、面开火时红方第i个单位对蓝方第j个单位的损耗系数，分别为直接开火、面开火时蓝方第j个单位对红方第i个单位的损耗系数，CR、CB分别为红方、蓝方兵种间的作战协同程度（该协同程度反映了作战单元对协同作战的增益情况），φij为蓝方第j个单位对红方第i个单位的火力分配系数，φji为红方第i个单位对蓝方第j个单位的火力分配系数，m和n分别为红方和蓝方兵种数量，。在此基础上构建多兵种非对称空战的常微分方程如下：

在分别构建了单一机种和多兵种空战的改进型兰彻斯特模型后，即可以通过计算机仿真来分析非对称空战背景下双方作战力量、信息力量和作战协同程度等对空战进程的影响情况。

4 仿真分析

4.1 单一机种非对称空战仿真

在仿真计算过程中，主要针对交战双方作战力量多少、信息力量强弱和作战协同优劣来分析非对称空战进程。作战力量多少主要体现在双方初始兵力情况（即F（R0）和G（B0））以及双方兵力补充速率（即LR和LB）；信息力量强弱主要体现在双方的发现概率P（Rh）和P（Bh）、（h）和（h）以及直接开火比例系数μR、μB，但是需要注意的是信息处于非对称优势的一方无论在直接开火还是面开火中发现概率都要大于信息劣势方，才能彰显其信息优势；作战协同优劣在单一机种仿真中暂不考虑。具体仿真过程可以分为如下几类：

①考虑作战力量非对称：先假设红方初始单一机群数量F（R0）=50，蓝方数量G（B0）=100，双方兵力补充速率LR=LB=5，双方直接开火形势下发现概率，击毁概率均取为1，表明“发现即摧毁”，面开火时发现概率，击毁概率均取为 0.5，直接开火比例 μR=μB=0.5，δR和 δB按照近年来各国空军飞机失事趋势均取为0.05，在单一机种模型基础上进行仿真计算，然后通过改变红蓝方力量对比，观察作战力量非对称下的空战进程，非对称初始兵力仿真如下页图1所示。

通过初始兵力的变化，可以发现在蓝方具备非对称力量优势的情况下，力量优势越明显，单一机种空战进程越快，并且非对称优势方损耗越小，那么在初始力量确定的情况下观察双方兵力补充速率对空战进程的影响如何，如下页图2所示。

由图2清楚地发现，初始兵力劣势方（红方）在增强兵力补充的过程中，劣势方凭借雄厚的后备空战力量逐渐扭转战场态势，当兵力补充速率达到某一程度时双方将会僵持下去，当劣势方兵力补充速率达到某一优势时，将会反败为胜。这也启示未来非对称空战指挥员在排兵布阵时要展现战略思维能力，初始优势并不代表战役胜利，即使是空中战场，也可以通过“化整为零”消耗对手、不断补充兵力战胜对手。

图1 非对称初始兵力仿真图

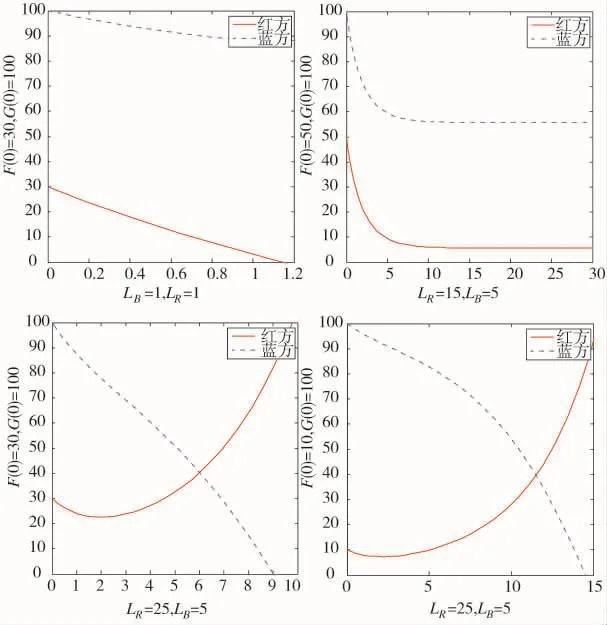
图2 非对称兵力补充速率仿真图

②考虑信息力量非对称：先假设红蓝双方交战的飞机数量FR（0）=GB（0）=100，双方兵力补充速率LR=LB=5，假设红方具备非对称的信息优势，比如强大的预警体系支撑、先进的机载雷达设备等，那么μR=0.5～1，μB=0～0.5，双方直接开火形势下发现概率P（Rh）≥P（Bh），面开火时发现概率（h）≥（h），通过改变参数来仿真计算，由图3观察信息优势对空战进程的影响。

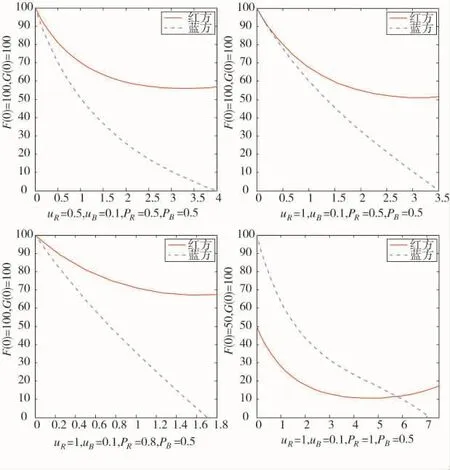
图3 非对称信息力量仿真图

在仿真图3中可以反映出信息非对称优势能够凭借信息力量优势快速建立起空战优势，信息优势越明显越能够快速解决战斗，并且通过信息力量的非对称优势可以弥补空战力量的劣势，扭转空战局势，取得最终胜利，特别是在高信息化对抗的空中战场，信息优势的建立、制信息权的掌控都是对战场进程至关重要的决胜因素。

4.2 多兵种非对称空战仿真

未来空战必然是多兵种、立体化的协同作战，多兵种空战必须要空空、空地和防空力量协同配合，单兵种作战力量的优势并不代表空战整体优势，只有建立协同优势，才能确保空战胜利。为简化多兵种非对称空战过程，现设定某空战背景下红蓝双方分别有歼击机部队、防空兵部队和轰炸机部队参战，红、蓝方歼击机数量FR1（0）=100、GB1（0）=100，防空火炮数量FR2（0）=100、GB2（0）=100，轰炸机数量FR3（0）=30、GB3（0）=30；红方对蓝方火力分配系数φ11=0.8、φ21=0、φ31=0.2、φ12=0.7、φ22=0、φ32=0.3、φ13=0、φ23=1、φ33=0，蓝方对红方火力分配系数 φ11=0.8、φ21=0、φ31=0.2、φ12=0.7、φ22=0、φ32=0.3、φ13=0、φ23=1、φ33=0；假设 δR=δB=0、LRi=LBj=0，即红蓝双方无非战斗减员和战斗补充；根据文献［2-3］中对武器装备作战效能指数的计算，令直接开火的αR11=16.8、αR21=0、αR31=16.8、αR12=23.4、αR22=0、αR32=23.4、αR13=0、αR23=18、αR33=0、βB11=14.4、βB21=0、βB31=14.4、βB12=20.2、βB22=0、βB32=20.2、βB13=0、βB23=18.8、βB33=0，令面开火的损耗系数为直接开火的一半；假设 CR=0.5，CB=0.5；μRi=0.5，μBj=0.5；在这些假设前提下，通过仿真观察整个空战进程如图4所示。

图4 多兵种非对称空战仿真

由图4（a）可以观察出多兵种空战模型仿真出来的空战进程，其中由于红方防空效能占优，导致蓝方歼击机率先被歼灭，继而红方歼击机损耗完毕；紧接着蓝、红方轰炸机相继损耗殆尽，最终红方剩余防空火炮数量多于蓝方，红方实际上取得了该多兵种空战的胜利。通过图4（a）可以很好地验证本文多兵种非对称空战模型的正确性。

通过图 4（b）、4（c）可以看到由于蓝方多兵种作战协同化程度高，或者叫作作战协同程度存在非对称优势，那么空战进程发生重大转变，蓝方对协同化程度一般的红方形成破竹之势，迅速扭转战局，最终取得胜利，即便红方在武器装备数量上比蓝方有非对称优势，也难以完全战胜高度协同化的蓝方，在未来非对称空战战场，各兵种之间协同作战的重要程度可见一斑。当然，由图4（d）可以说明，作战协同处于劣势的一方，需要作战效能更高的空战兵器、更加强大的信息支援能力等才能够有击败对方的可能。

5 结论

本文从对未来非对称空战进行进程预测的视角出发，在传统的兰彻斯特方法基础上进行加工改进，构建了一种用于非对称空战预测的新型兰彻斯特方程，得到了基于该新型兰彻斯特方程的非对称空战进程预测方法，并对其模型进行仿真验证。通过仿真，发现该模型符合非对称空战背景下的客观规律，能够有效预测未来非对称空战进程；并且通过对作战力量、信息力量和作战协同度等几个空战影响因子进行数学实验，为空战战术运用和武器装备发展等提供了一定的建设性意见。

［1］XU H J，GUO H.Air combat mathematical models and efficiency evaluation ［M］.Beijing：National Defense Industry Press，2010.

［2］XU X W，WANG S Y.Modern combat simulation［M］.Beijing：Science Press，2004.

［3］LUO X M.Asymmetric operation mathematical modeling and simulation analysis［M］.Beijing：National Defense Industry Press，2012.

［4］GUO Q S.Military equipment warfighting simulation［M］.Beijing：National Defense Industry Press，2013.

［5］郭辉，徐浩军，谷向东.基于改进兰彻斯特平方律的空战进程预测研究［J］.火力与指挥控制，2010，35（9）：50-52.

［6］吴俊，杨峰，梁彦.面向信息化战争的广义兰彻斯特作战模型［J］.火力与指挥控制，2010，35（2）：50-53.

［7］HUANG F，LI A P，SHANG C A.Application on Lanchester fight theory in antiaircraft fight ［J］.Journal of Air Force Engineering University，2003，4（6）：34-36.

［8］CHEN X Y，JING Y W，LI C J，et al.Optimal strategies for winning in military conflicts based on Lanchester equation［J］.Control and Decision，2011，26（6）：945-948.

［9］ZHAN D H，CHEN G，ZHANG H J，et al.Lanchester combat model in conditions of modernized warfare ［J］.Computer Engineering and Applications，2011，26（6）：945-948.

［10］KANG C L.National defence system analysis method［M］.Beijing：National Defense Industry Press，2003.

［11］CHEN X Y，JING Y W，LI C J.Warfare command stratagem analysis for winning based on lanchester attrition models ［J］.Journal of Systems Science and Systems Engineering，2012，21（1）：94-105.

［12］ZHOU L Z.Emulational method and its principle computing win-probabilities for Lanchester operational course［J］.Control and Decision，2009，21（11）：3171-3179.

Forecast of Asymmetric Air Combat Course Based on New Lanchester Equation

ZHANG Yang-ming，CHEN Yun-xiang，CAI Zhong-yi，XIANG Hua-chun
（School of Equipment Management and Safety Engineering，Air Force Engineering University，Xi’an 710051，China）

Aiming at researching on the asymmetric air combat problem which maybe appear in the future，the paper finds a new Lanchester equation to analyze this problem within the hypothetical background of asymmetric air combat.Some Simulations are made to verify the effectiveness of this new method and its models，and some guidance will be offered to the decision of asymmetric air combat.

new Lanchester equation，asymmetric air combat，course forecast

C93；TJ86

：A

10.3969/j.issn.1002-0640.2017.06.024

2016-05-09

：2016-06-23

张洋铭（1988- ），男，山东烟台人，博士生。研究方向：装备管理与决策。

1002-0640（2017）06-0105-05