X波段导航雷达海浪数值模拟
马狄席泽敏包中华
(海军工程大学武汉430033)
X波段导航雷达海浪数值模拟
马狄席泽敏包中华
(海军工程大学武汉430033)
针对X波段导航雷达海浪特性研究的需要,对海浪进行了数值模拟。采用经典PM谱作为靶谱,利用Longuest—Higgins模型仿真海浪,然后对仿真的海浪进行阴影调制和倾斜调制得到调制后的雷达图像,并经过海浪谱反演技术验证了仿真的可行性和准确性。
X波段雷达;PM谱;阴影调制;倾斜调制;反演
Class NumberTN957.52
1 引言
X波段雷达通过电磁波照射海面成像,形成了“海杂波”图像,不仅能检测海上目标,同时也能从图像中可以得到海浪的流速、波向等信息。为了更好了解海浪产生过程,理解雷达对海浪调制机理,分析海浪在导航雷达中的成像机理及其谱的特性,本文对经过雷达调制后的海浪进行了模拟仿真。
2 海浪数值模拟
2.1 海浪模型
由线性重力波相关理论可知,窄带谱的高斯随机过程可以用来描述海面波场在时间空间上的分布,即Longuest—Higgins模型[1],海面波某一位置的高度η(x,y,t)可以用不同频率、不同波矢和随机相位的余弦波组成,海面波高的具体表达式如下:
式中Amn为沿着波矢量(kxm,kyn)的幅度,ωmn为角频率,与kxmkyn成频散关系,(x,y)海面上的空间坐标,δmn为[] 02π均匀分布的随机相位。幅度Amn由二维谱P(ωm,θn)求得:
2.2 海浪模拟
2.2.1 PM谱
为了求解二维波数谱P(ωm,θn),进而求解海面波高,需要选择合适海浪谱和方向谱函数,本文中采用的是由1978年第15届ITTC(国际拖曳水池会议)采用的PM谱[2],如下所示:
式中θ为组成波的方向,θ0为主波方向,由随机波浪理论可知组成波的能量的角度θ-θ0分布在
式中Hs为海浪的有效波高,T01为海浪的平均周期。
2.2.2 方向分布函数
只有波数谱还不足以描述海浪的特性,在研究海蓝绕射、折射等运动时,要用到方向谱,因此考虑波浪的方向分布函数[3]具有重要的意义。
本文采用的是经验公式如下:
2.3 海浪数值仿真
由海浪模型可知,二维谱P(ωm,θn)求解得到后便可求出海面波高中的Amn,进而求解出海面波高。仿真海浪图如下所示。
3 雷达调制海浪
雷达对于海杂波主要有阴影、倾斜、轨道和流体力学调制四种调制[5]方法。在远距离掠射角下起重要作用的是阴影调制和倾斜调制[6]。
3.1 阴影调制
X波段导航雷达的电磁波远距离射向海表面的时,形成了很低的掠射角(在很远距离几乎与海表面平行),此时波面较低的海浪被前面较高的波浪遮挡,使得电磁波无法到达较低的波浪,具体实现方法如下。
由图3可设雷达电磁波掠射到海平面面元(x,y,t)的掠射角θ为
式中R(x,y)是面元到天线的水平距离,Λ是天线高度,则在该面元前面的另一面元(x',y',t)(即水平距离R(x',y',t)<R(x,y,t))的俯角θ(x',y',t)≥θ(x,y,t),则该面元被遮挡,阴影调制具体方法如下:
其中σ(x,y,t)为η(x,y,t)分为256个灰度值所得结果。
3.2 倾斜调制
倾斜调制主要是由于海浪中存在大尺度的海浪成分,导致了电磁波后向散射面积单元发线方向的改变,导致入射角发生变化进而影响后向截面积的变化。当波向朝向雷达时倾斜调制最强,背离时最弱。
由图3可知:倾斜调制主要由俯角和水平距离进行判决,具体实现方法如下:
面元(x,y)的外法线单位矢量为
式中(lx,ly,lz)为雷达天线所在空间坐标。
用海平面的切矢量和单位矢量的点积来表示倾斜调制的结果:
3.3 两种综合调制
两种综合调制后的实现如下所示。
否则,在其他条件,两种综合调制的结果为0。
3.4 仿真图像
根据阴影调制和倾斜调制上述机理进行雷达海杂波图像仿真时,设置X波段导航雷达的参数如表1所示。线方向的单位矢量u⇀为
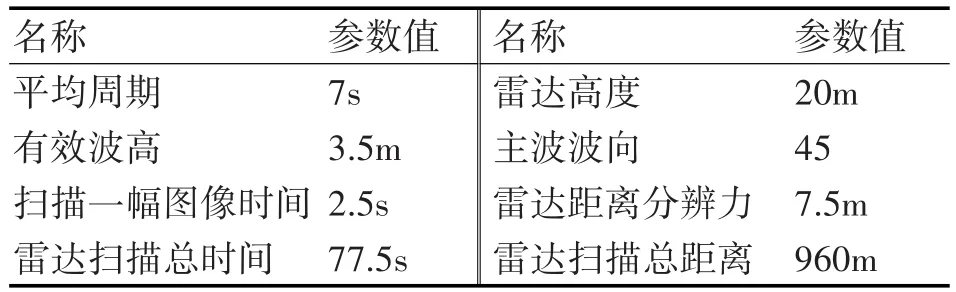
表1 X波段导航雷达海杂波图像仿真参数
按照上述仿真参数进行仿真,得到两种综合调制后海浪波高图像如图4所示。
在图4图像中心位置为雷达所在位置,由图像可以看出:离雷达位置越远,阴影调制越明显,这也验证了阴调制的原理。
4 反演结果及分析
将仿真后的海浪数据进行海浪谱相关参数的反演,具体的流程图如图5所示。
将经过雷达调制后的海浪波高数据进行3维FFT变换后得到3维图像谱[7],再经高通、带通滤波[8],积分后得到二维图像谱,对二维图像谱进行处理得到海浪最终的平均波向、平均周期等参数信息。
反演出的一维频谱与输入的一维频谱如图6所示。
由图6可知:反演的一维频谱与输入的一维频谱峰频重合,其他部分趋势一致,验证了仿真的正确性和有效性。
反演结果如表2所示。
上述的反演结果与崔利民[9]在其博士文中结果和周蓓[10]在其硕士论文中结果相比较为符合,同样验证了仿真的准确性和有效性。
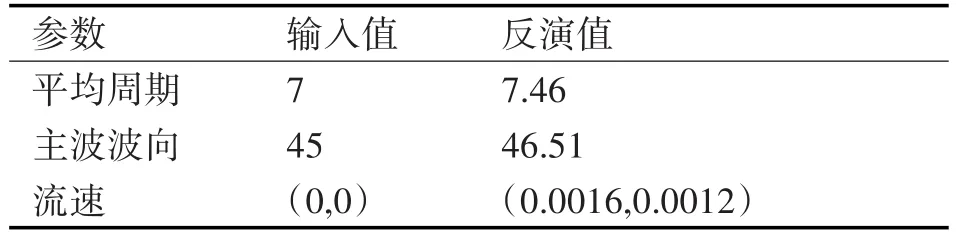
表2 反演仿真数据结果
5 结语
本文主要仿真了经过雷达调制海浪波高,并通过海浪谱的反演技术反演出海浪的相关参数并与输入参数做了对比,验证了仿真的正确性和有效性。
由于仿真时海浪参数、模拟海浪时的随机相位以及雷达参数都将对模拟结果造成不同的影响,接下来将在参数影响[11]方面和流速反演[12]方面进行进一步的研究。
[1]文圣常,余宙文.海浪理论与计算原理[M].北京.科学出版社,1984:130.
[2]俞津修.随机波浪及其工程应用[M].大连:大连理工大学出版社,2000:157.
[3]文圣常,余宙文.海浪理论与计算原理[M].北京:科学出版社,1984:159.
[4]俞津修.随机波浪及其工程应用[M].大连:大连理工大学出版社,2000:182.
[5]蔡文娟.岸基X波段宽带相参雷达海浪信息提取技术研究[D].哈尔滨:哈尔滨工业大学,2014:13-15.
[6]杨亚东.X波段海浪信息参数反演算法研究[D].成都:电子科技大学,2014:41-43.
[7]邹塞.X波段宽带相参雷达海面回波信息反演技术研究[D].哈尔滨:哈尔滨工业大学,2015:23-32.
[8]周蓓.X波段雷达海面流场信息提取技术研究[D].青岛:中国海洋大学,2008:11.
[9]崔利民.X波段雷达海浪与海流遥感机理及信息提取方法研究[D].青岛:中国科学院海洋研究所,2010:51-57.
[10]周蓓.X波段雷达海面流场信息提取技术研究[D].青岛:中国海洋大学,2008:28.
[11]骆小谚.海浪极化SAR成像模拟及反演技术研究[D].成都:电子科技大学,2008:32-35.
[12]Nieto Borge J C.Inversion of marine radar images for surface wave analysis[J].Journal of Atmospheric and Oceanic Technology,2004,21(8):1291-1300.
Numerical Simulation of Radar Wave in X-Band Navigation
MA DiXI ZeminBAO Zhonghua
(Naval University of Engineering,Wuhan430033)
Aiming at the need of the study of the characteristics of the wave of the x-band navigation radar,the numerical simulation has been done.Using the classical PM spectrum as the target spectrum,the Longuest-Higgins model is used to simulate the waves,and then the simulated waves are subjected to shadow modulation and tilt modulation.The modulated radar images are obtained and the feasibility and accuracy of the simulation are verified by the wave spectrum inversion technique.
X-band radar,PM spectrum,shadow modulation,tilt modulation,inversion
TN957.52
10.3969/j.issn.1672-9730.2017.07.012
2017年1月7日,
2017年2月10日
马狄,男,硕士,研究方向:目标成像与识别。席泽敏,男,博士,副教授,研究方向:目标成像与识别。包中华,男,博士,讲师,研究方向:雷达信号处理、导航雷达海态反演。

