围长至少为5的平面图的injective染色*

卜月华, 叶飘飘

(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.浙江师范大学 行知学院,浙江 金华 321004)



围长至少为5的平面图的injective染色*

卜月华1,2, 叶飘飘1

(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.浙江师范大学 行知学院,浙江 金华 321004)

通过构造一个(Δ+3)-临界图G,运用权转移的方法证明了该图G不存在.同时，用反证法证明了：对于围长至少为5的平面图G,若Δ(G)≥30,则χi(G)≤Δ+3.这个结论改进了现有的一个结果.

平面图;围长;injective染色;面

0 引 言

本文仅考虑有限简单图.对于一个平面图G,把它的顶点集、边集、面集、最大度、最小度、围长及图G中u,v间的距离分别记作V(G),E(G),F(G),Δ(G),δ(G),g(G)和dG(u,v).对于图G的一个顶点v,若d(v)=k(或d(v)≥k,或d(v)≤k),则称v为一个k-点(或k+-点,或k--点).对平面图的面也可以类似定义.∀f∈F(G),记B(f)为面f的边界迹.若u1u2…un在B(f)上按顺时针排列,则面f记为f=[u1u2…un].围长g(G)表示图G中最短圈的长度.

图G的正常顶点染色是指对图G的每个顶点分配一种颜色,使得相邻的2个顶点染不同色,其所需的最少颜色数称为图G的色数,记为χ(G).图G的injectivek-染色是指映射c:V(G)→{1,2,…,k},使得有公共邻点的2个顶点u,v满足c(u)≠c(v).若图G有一个injectivek-染色,则称图G是injectivek-可染的,并称χi(G)=min{k|G是injectivek-可染的}为图G的injective色数.

Injective染色是由Hahn等[1]提出,并且证明了对任意的平面图G都有Δ(G)≤χi(G)≤(Δ(G))2-Δ(G)+1.随后,人们对平面图的injective染色问题展开了一系列的研究.Doyon等[2]证明了:对任意围长为g(G)且最大度为Δ的平面图G,有:若g(G)≥7,则χi(G)≤Δ+3;若g(G)≥6,则χi(G)≤Δ+4;若g(G)≥5,则χi(G)≤Δ+8.文献[2-5]研究了稀疏图和平面图的injective色数的上界问题.文献[6]证明了:对于围长g(G)≥6的平面图G,χi(G)≤Δ+3;若Δ≥9,则χi(G)≤Δ+2;若Δ≥17,则χi(G)≤Δ+1.文献[7]证明了:对于围长为g(G)≥5的平面图G,χi(G)≤Δ+6;若Δ≥35,则χi(G)≤Δ+3.

问题1 是否存在一个整数M,使得g(G)≥5且Δ≥M的平面图G是injective (Δ+1)-可染的？

本文研究围长为g(G)≥5的平面图G的injective染色,证明了下面这个定理:

定理1 若图G是g(G)≥5,Δ(G)≥30的平面图,则χi(G)≤Δ(G)+3.

1 临界图的构型

若图G不是injectivek-可染,但是它的任意真子图都是injectivek-可染,则称这样的图G为k-临界图.接下来将研究k-临界图的一些性质.

设c是图G的injective染色,顶点v所染的颜色记作c(v),对G的一个顶点子集S,所染的颜色集记作c(S)={c(v) | v∈S}.

以下是k-临界图G(k≥Δ+1)的一些性质,其证明可见文献[6].

性质1 设图G是k-临界图,其中k≥Δ+1,uv∈E(G).若D(u)≤k-1+d(u),则D(v)≥k+d(v).

性质2 设图G是(Δ+t)-临界图,其中t≥1,则G不包含相邻2-点且δ(G)≥2.

性质3 设图G是(Δ+t)-临界图,其中t≥1,v是2-点,记N(v)={v1,v2}.若D(v)≤Δ+t+1,则∀i∈{1,2},D(vi)≥Δ+t+d(vi).

性质4 设图G是(Δ+t)-临界图,其中t≥1,v是3-点,记N(v)={v1,v2,v3}.若D(v)≤Δ+t+2,则∀i∈{1,2,3},D(vi)≥Δ+t+d(vi).

由性质4可知,轻3(0)-点与轻3(0)-点不相邻.

2 定理1的证明

下面用反证法证明定理1.若定理1的结论不成立,则存在平面图 G′,使g(G′)≥5,Δ(G′)≥30,但χ(G′)>Δ(G′)+3.令图G是一个满足Δ(G)≤Δ(G′)=Δ,g(G)≥5,χ(G)>Δ+3且|E(G)|+|V(G)|最小的平面图,则图G是(Δ+3)-临界图.显然,图G是连通图且δ(G)≥2.

记ε=1/5.用权转移方法证明G是不存在的.

下面根据G的结构性质,在保持总权和不变的情况下,对G中的点和面的权按一定规则进行转移,得到一个新的权函数w*(x).下面将证明:对任意x∈V∪F,都有w*(x)≥0,从而得出如下矛盾:

这个矛盾说明G不存在,从而定理1是成立的.

权转移分2步进行.第1步:对∀x∈V∪F,设置初始权为w(x).运用一些转权规则,将证明除一些5-点、6-点外的任意顶点和面得到的新权w′(x)≥0.第 2 步:将对于这些权小于零的顶点定义新的转权规则,得到的新权记为w*(x)，并将证明w*(x)≥0.

定义以下权转移规则:

R1:3≤d(v)≤9的点v给相邻的轻2-点转权1;

R3:若4≤d(v)≤9,则v给相邻的3(1)-点转权ε;

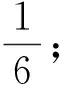
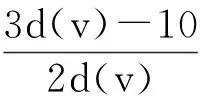
记 f是G的k-面.因为k≥5,所以对∀f∈F(G),w′(f)=d(f)-5≥0.

对于顶点v,设d(v)=k,则由性质2知 k≥2.

3)k=4,w(v)=1.因为d(v)=4,所以与v相邻的每个2-点都是轻2-点.

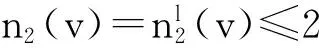
在运用第1次权转移规则后,对∀x∈V(G)∪F(G),除了一些5-点和6-点外,其余的顶点和面都有非负的权值.称这些权值可能为负的5-点和6-点为坏5-点和坏6-点;称权值非负的顶点为好点.综上讨论,存在4种可能的坏5-点和坏6-点.

对uv∈E(G),若d(u)≥10,d(v)≥10,则称uv为特殊边.

第2次权转移规则R6～R8:

R7:每个2≤k≤9的k-点v将多余的权值平均转给每个关联面;

R8:通过R6,R7转权后,每个5+-面 f将多余的权值平均转给面 f上可能的坏5-点和坏6-点.

运用第2次转权规则之后,把∀x∈V(G)∪F(G)的新权记为w*(x).

反证法 若4≤d(w1)≤5,则可设d(u1)=2.由G的极小性知,G-vw有一个(Δ+3)-injective染色c.先擦去v和w的颜色.若|c(N2(v))|≤Δ+2,则可以把c延拓到整个图G.因为w的禁用色至多是8,所以w可以被正常染好.否则,设 |c(N2(v))|≥Δ+3.因为|N2(v)|=Δ+3,所以|c(N2(v))|=Δ+3.考虑 u1,易知擦去v和w的颜色之后,|c(N2(u1))|≤Δ+1,可以用c(u1)染v,再把u1染好,最后染w.这样,c就成为G的一个(Δ+3)-injective染色.与假设矛盾.断言1证毕.

下面分4种情形讨论坏5-点和坏6-点最终的权.

若v不关联6+-面,则v恰好关联5个5-面.有{w1x1,x1y1,y1z1,z1u2,u1w1}⊆E(G),其中u1,u2∈N(u).记 f1=[uvww1u1],f2=[zvuu2z1],f3=[yvzz1y1],f4=[xvyy1x1].若d(u1)≥10,则uu1是特殊边,由R6 知,面 f1至少可以从u,u1获得权1.因为v是面 f1中唯一的坏5-点或坏6-点, 所以由R8 知, v从面 f1获得权 1.因此,w*(v)≥w′(v)+1>0.类似地,若d(u2)≥10,则 w*(v)≥0.下面仅考虑d(u1)≤9,d(u2)≤9.

②w1和z1中至少有1个为9--点,不妨设3≤d(z1)≤9.因为z是轻2-点,所以由性质3知,D(z1)≥Δ+3+d(z1).

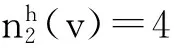
通过2次权转移就检验了对任意x∈V(G)∪F(G),都有w*(x)≥0,从而得到矛盾.定理1证毕.

3 结 语

本文讨论了围长至少为5的平面图的injective染色问题,证明了:若图G是 g(G)≥5,Δ(G)≥30的平面图,则χi(G)≤Δ(G)+3.根据文献[7]的结论和本文结果,下面这个问题是有意义的,即:对于g(G)≥5的平面图G,探讨最小的正整数Δ0,使得当Δ(G)≥Δ0时,有χi(G)≤Δ(G)+3.

[1]Hahn G,Kratochvíl J,Sirá J,et al.On the injective chromatic number of graphs[J].Discrete Math,2002,256(1/2):179-192.

[2]Doyon A,Hahn G,Raspaud A.Some bounds on the injective chromatic number of graphs[J].Discrete Math,2012,310(3):585-590.

[3]Cranston D,Kim S,Yu G.Injective colorings of graphs with low average degree[J].Algorithmica,2010,60(3):553-568.

[4]Cranston D,Kim S,Yu G.Injective colorings of sparse graphs[J].Discrete Math,2010,310(21):2965-2973.

[5]Bu Y,Chen D,Raspaud A,et al.Injective coloring of planar graphs[J].Discrete Appl Math,2009,157(4):663-672.

[6]Dong W,Lin W.Injective coloring of planar graphs with girth 6[J].Discrete Math,2013,313(12):1302-1311.

[7]Dong W,Lin W.Injective coloring of plane graphs with girth 5[J].Discrete Math,2014,315/316(12):120-127.

(责任编辑 陶立方)

Injective coloring of planar graphs with grith 5

BU Yuehua1,2, YE Piaopiao1

(1.CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China; 2.XingzhiCollege,ZhejiangNormalUniversity,Jinhua321004,China)

LetGbe a plane graph withg(G)≥5 andχi(G) be the injective chromatic number ofG. It was improved some known results by proving thatχi(G)≤Δ+3 whenΔ(G)≥30. The result was obtained by contradiction: LetGbe a (Δ+3)-critical graph, a discharging procedure was applied to the proof by showing thatGcould not exist.

planar graph; grith; injective coloring; face

10.16218/j.issn.1001-5051.2017.01.001

2016-04-23；

2016-05-29

国家自然科学基金资助项目(11271334)

卜月华(1960-)，男，浙江东阳人，教授，博士生导师.研究方向：组合数学与图论.

O157.5

A

1001-5051(2017)01-0001-08