基于分支定界和模拟退火算法的成爆弹型弹量计算模型
李亚雄,刘新学,徐 萌
(1 火箭军工程大学,西安 710025; 2.中国人民解放军31102部队, 南京 210016)
基于分支定界和模拟退火算法的成爆弹型弹量计算模型
李亚雄1,刘新学1,徐 萌2
(1 火箭军工程大学,西安 710025; 2.中国人民解放军31102部队, 南京 210016)
在多型导弹组合打击模式下,对同一目标打击存在多种混合火力弹型弹量组合方案;如何选出既满足毁伤要求,耗弹量又尽可能少的组合方案是决策者关心的重大问题;针对该问题决策变量维数高的特点,基于分支定界算法和模拟退火算法,建立了两种成爆弹型弹量计算模型,设计了两种算法组合使用方法;算例分析表明:建立的模型具有较高的计算效率和全局寻优能力,具有重要的工程应用价值。
分支定界;模拟退火;弹型弹量
目前,对于导弹成爆弹量计算的研究主要基于单弹型打击的前提,并没有区分弹型的差异。比如,文献[1]基于导弹对目标的命中弹数指标要求和单发命中概率,给出了单目标成爆弹量的计算模型。文献[2]分析研究了目标网格分割粒度、仿真次数对成爆弹量计算精度的影响。文献[3]基于对机场内部子系统的串、并联结构与机场保障能力的关系,给出了摧毁机场目标最大保障能力的耗弹量计算模型。在上述研究中,目标毁伤效果f与成爆弹量N之间的函数关系f(N)属于单调递增关系,决策变量为一维变量,满足打击要求的最小弹量即为所需要的成爆弹量,计算结果是唯一的。在混合火力打击条件下,由于弹型选择的多样性,在总耗弹量相同的情况下,满足打击要求的弹型弹量组合通常有多种方案。除了导弹数量,弹型也是重要的决策变量,变量维数的增加极大地提高了计算的复杂度。另外,在混合火力打击模式下,“基于物理”的武器毁伤效果评估与单弹型打击相比有着结构性的差异,涉及目标易损性,系统结构、功能评价等问题。本文重点对获得毁伤效能评估基础上弹型弹量的优化计算问题进行研究。
1 成爆弹型弹量计算问题数学模型
1.1 成爆弹型弹量计算问题数学模型构建
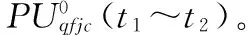
混合火力打击成爆弹型弹量计算问题可用式(1)所示的数学规划模型表示:
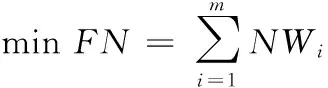
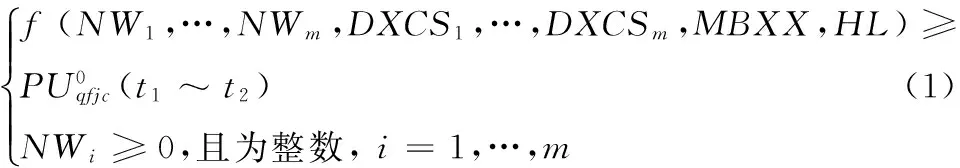
式中:FN为总耗弹量;NWi为第i种弹型的成爆弹量,为该问题的决策变量,i=1,2,…,m;DXCSi为第i种弹型的战技参数,i=1,2,…,m;MBXX为计算毁伤效果需要的目标参数;HL为混合火力子目标和瞄准点分配方案;f(*)为混合火力打击获得的毁伤效果。
1.2 成爆弹型弹量计算问题数学模型特点

1.3 成爆弹型弹量计算问题的求解思路
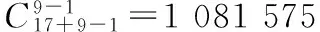
2 基于分支定界算法的成爆弹型弹量计算模型
2.1 分支定界法简介
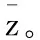
2.2 基于分支定界算法的成爆弹型弹量计算步骤
基于分支定界算法的成爆弹型弹量计算步骤如下:
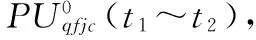
步骤2:进行增加弹数分支,分别将每种弹型的弹数增加1枚,得到m个成爆弹数相同的弹型弹量组合方案,每个方案称为一个分支。计算这m个方案对目标打击的毁伤效果,对满足毁伤要求的方案停止增加弹数分支,转入步骤3。如果所有分支均不满足毁伤要求,则选择毁伤效果指标值最好的分支,减去其余分支,重复步骤2,继续进行增加弹数分支。
步骤3:进行减少弹数分支,分别将每种弹型的弹数减去1枚,得到m个成爆弹数相同的弹型弹量组合方案,每个方案称为一个分支。计算这m个方案对目标打击的毁伤效果,减去不满足毁伤要求的分支,若所有分支均被减去,则分支前的弹型弹量组合为即为满足打击要求的耗弹量最小的方案;对没有减去的分支,重复上述过程,直到所有分支都被减去为止。
需要指出的是,分支定界法用于解决线性整数规划问题时能够得到完备的整数解集,而成爆弹型弹量计算问题属于非线性NP完全问题,运用分支定界的思想求解得到的解属于准优解,不能保证全局最优。
3 基于模拟退火算法的弹型弹量计算模型
3.1 模型的基本概念
在模拟退火算法中,自然界的金属物体涉及状态、能量最低的状态和能量等概念;组合优化算法中涉及解、最优解、目标函数等概念;在求解成爆弹型弹量时,涉及组合方案、满足要求的方案、总耗弹量等概念。其相互关系如表1所示。

表1 成爆弹型弹量计算模型相关概念
3.2 初始解集的构造和领域结构
根据模拟退火算法的基本原理,结合成爆弹型弹量计算模型的特点,给出两种构造初始解集的方法。
方法1:为了得到满足打击要求的混合火力打击弹型弹量方案集,在利用模拟退火算法求解时,采用多起点策略,若有弹型m种,则初始解的规模设为m。不失一般性,可以从分别设每种弹型为1枚弹作为初始解集,如表2所示。

表2 模拟退火算法的初始解集
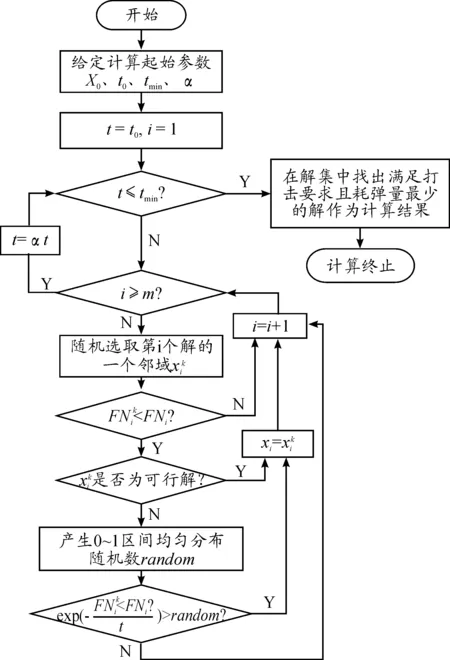
方法2:为提高计算效率,可以先由基于分支定界算法的计算模型得到L个满足打击要求的可行解,当L=m时,直接将其作为初始解集;当L>m时,随机选取其中m个作为初始解集;当L 3.3 温度参数的控制 模拟退火算法中包含内外两重循环,其中外层循环靠温度的下降进行控制,内层循环靠每一温度迭代长度控制。温度参数是模拟退火算法的关键参数之一,主要包括起始温度的选取、温度的下降方法、停止温度和每一温度的迭代长度。 1) 起始温度。起始温度t0应保证平稳分布中每一状态的概率相等,即满足下式: (2) 式中:ΔFNij为第j次迭代和第i次迭代的目标函数差,ΔFNij=FN(j)-FN(i)。 很容易得到t0的估计值为 t0=KΔ0 (3) 式中:K为充分大的数,实际计算中,可以选K=10,20,100,…的试验值。 Δ0按下式计算: (4) 对于具体的成爆弹型弹量计算问题,可以按照上式对Δ0进行估计。 2) 温度下降方法。温度下降采用最常用的相同比率下降法,即温度tk+1=αtk,其中0<α<1,α越接近1,温度下降越慢。 3) 终止温度及算法的终止原则。模拟退火的最终温度为0,最简单的原则是给定一个比较小的正数tmin,当温度t≤tmin时,算法停止。 4) 每一温度的迭代长度。根据成爆弹型弹量计算问题的特点,采用固定长度的方法确定每一温度的迭代步数。根据与邻域大小相关的规则,迭代长度可设为弹型数量m。 3.4 解的接受机制 区分两种初始解集的生成方法,建立不同接受机制。 3.5 算法计算流程设计 基于模拟退火算法的成爆弹型弹量计算,如果按照方法1生成初始解集,计算流程如图1所示;如果按照方法2生成初始解集,计算流程如图2所示。 图1 成爆弹型弹量计算流程(方法1) 4.1 问题背景 问题背景:用甲型侵彻子母弹、乙型侵彻子母弹和丙型延时子母弹等3种弹型对机场跑道进行混合火力打击(目标和武器参数略)。打击要求为跑道0~60 min内起飞飞机数平均下降率不小于0.6。求能够完成上述任务的混合火力成爆弹型弹量。 4.2 分支定界算法及结果分析 运用分支定界算法对问题进行求解,计算步骤如图3所示。 图2 成爆弹型弹量计算流程(方法2) 由于没有对所有方案进行遍历,而且打击效果与弹型弹量的关系并不是线性关系,因此基于分支定界算法得到的弹型弹量组合方案只是“准优解”不一定是耗弹量最少的方案。例如,在耗弹量为7枚的36种弹型弹量组合方案中,共有5种方案对目标的毁伤效果能够满足要求,在耗弹量为6枚的28种弹型弹量组合方案中,共有2种方案对目标的毁伤效果能够满足要求。实际通常在对计算时间快速性要求很高的条件下应用该方法,或者将其计算结果作为智能优化计算方法的初始解,以加快收敛速度。 图3 基于分支定界算法的成爆弹型弹量计算 4.3 模拟退火算法及结果分析 设定起始计算参数,t0=100,tmin=0.1,α=0.7。为便于比较两种成爆弹型弹量计算问题的计算效率,运用枚举法、基于分支定界算法的计算模型、基于模拟退火算法的计算模型3种方法的计算结果和计算效率对比如表3所示。 表3 成爆弹型弹量计算结果对比 如表3所示,对于该计算实例,基于分支定界算法的计算模型求解结果不是全局最优解,而是“准优解”,基于模拟退火算法的计算模型能够得到全局最优解,采用普通方法生成初始解的模拟退火算法比枚举法能够提高2.4倍的计算效率,如果采用分支定界法得到的解为初始解,能够提高9.1倍的计算效率,表明该方法综合了分支定界计算的快速性和模拟退火算法全局寻优能力,是解决打击要求给定的混合火力成爆弹型弹量计算问题的有效方法。 分析了混合火力打击弹型弹量计算问题与传统成爆弹量计算问题的差异,建立了数学模型,分析了模型特点,分别基于分支定界算法和模拟退火算法,构建了成爆弹型弹量计算模型,两种方法各有优点,将两种模型组合使用较好地解决了具有高维变量的混合火力成爆弹型弹量计算问题。在工程应用实际中,由于决策变量的多维性,在总耗弹量相同或相近的前提下,满足毁伤要求的弹型弹量通常有多种组合方案。对这些组合方案优选时,不能仅仅考虑总弹量一个指标,需要从工程应用实际出发,综合考虑多种因素。比如,作战部队、作战地域的协同使用问题,以及各型导弹武器的库存量、补充周期等因素。对于弹量组合方案的综合优选将是下一步需要研究解决的问题。 [1] 肖旭青,周奕,黄伟,等.成爆弹量预测模型研究[J].兵工自动化,2010,29(4):12-14. [2] 史宏亮,齐少军,刘忠仕,等.基于数值仿真的面杀伤战斗部对面目标成爆弹量计算方法[J].战术导弹技术,2010(3):53-56. [3] 张红文,陈智江,毕义明.基于遗传算法的机场目标耗弹量优化方法[J].火力指挥与控制,2007,32(8):84-86. [4] 邢文训,谢金星.现代优化计算方法[M].北京:清华大学出版社,2005. [5] 曾剑新,周焰,张斌.基于模拟退火和共同进化算法的协同航路规划[J].火力指挥与控制,2011,36(12):34-39. [6] 《运筹学》教材编写组.运筹学[M].北京:清华大学出版社,2005. (责任编辑 周江川) Model for Calculating the Quantity of the Bomb Based on the Branch-Bound and Simulated Annealing Algorithm LI Yaxiong1, LIU Xinxue1, XU Meng2 (1.Rocket Force University of Engineering, Xi’an 710025, China; 2.The No. 31102ndTroop of PLA, Nanjing 210016, China) In the multi mode missile combined attack mode, there are many kinds of combination scheme for the same target attack. How to choose the combination scheme that meets the requirements of the damage, and the quantity of the quantity of ammunition as few as possible is a major concern of the decision maker. To solve the problem of high dimension of decision variables, and based on the branch and bound algorithm and the simulated annealing algorithm, two kinds of calculation models for the amount of kinds of bomb are established, and the combination of the two algorithms is designed. Example analysis shows that the model has high computational efficiency and global optimization ability, and it has important engineering application value. branch and bound; simulated annealing; bomb quantity 10.11809/scbgxb2017.07.005 2017-03-13; 2017-04-10 李亚雄(1979—),男,博士,副教授,主要从事军事运筹学研究。 format:LI Yaxiong,LIU Xinxue,XU Meng.Model for Calculating the Quantity of the Bomb Based on the Branch-Bound and Simulated Annealing Algorithm[J].Journal of Ordnance Equipment Engineering,2017(7):20-24. TJ765 A 2096-2304(2017)07-0020-05 本文引用格式:李亚雄,刘新学,徐萌.基于分支定界和模拟退火算法的成爆弹型弹量计算模型[J].兵器装备工程学报,2017(7):20-24.
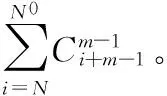

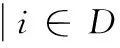
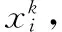
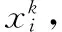
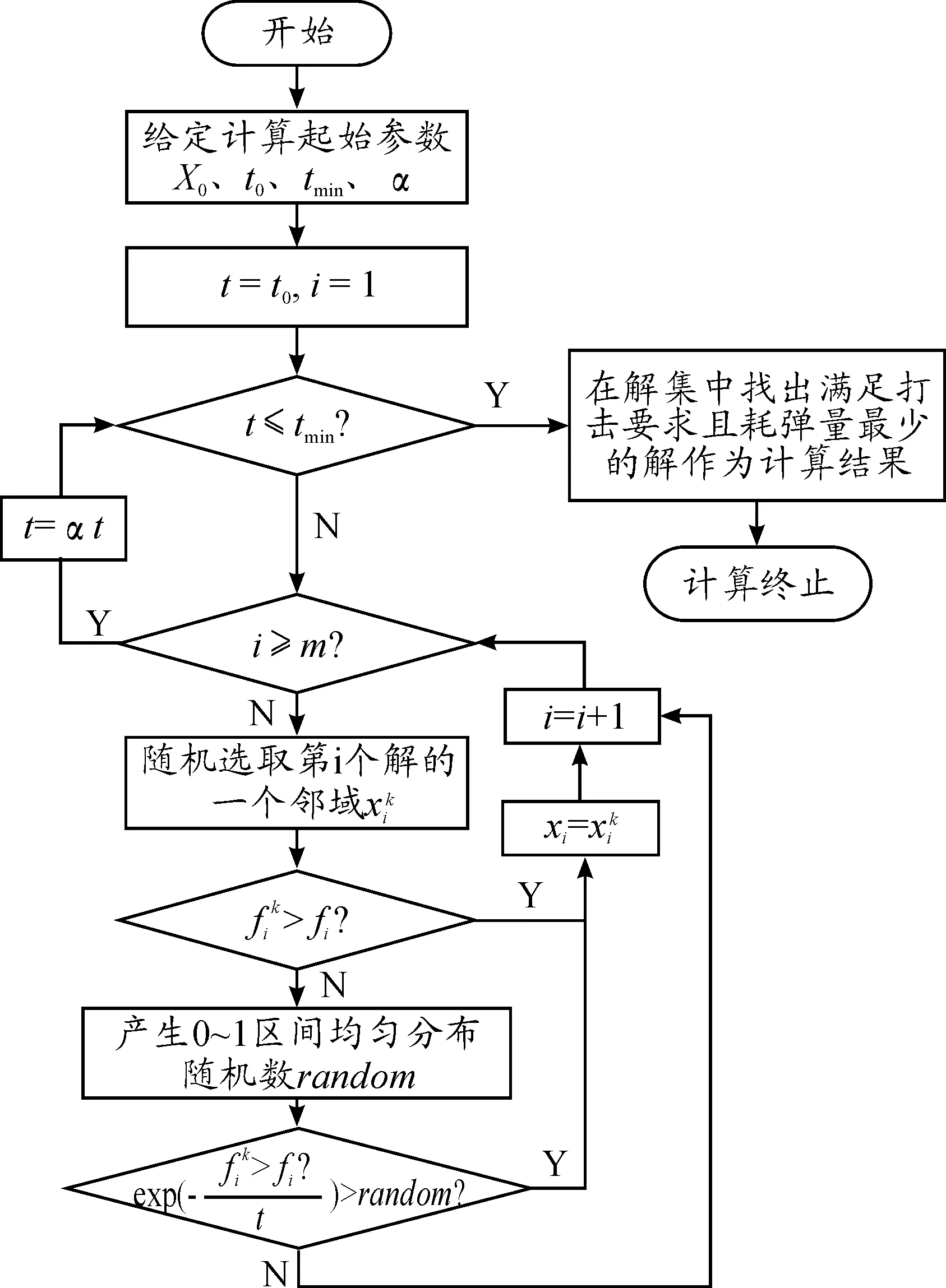
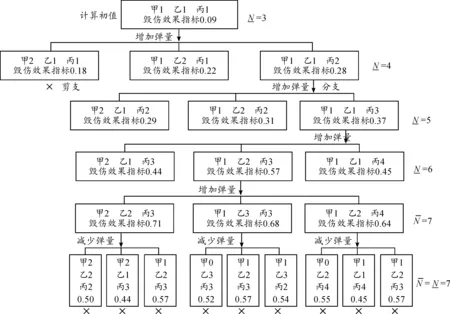
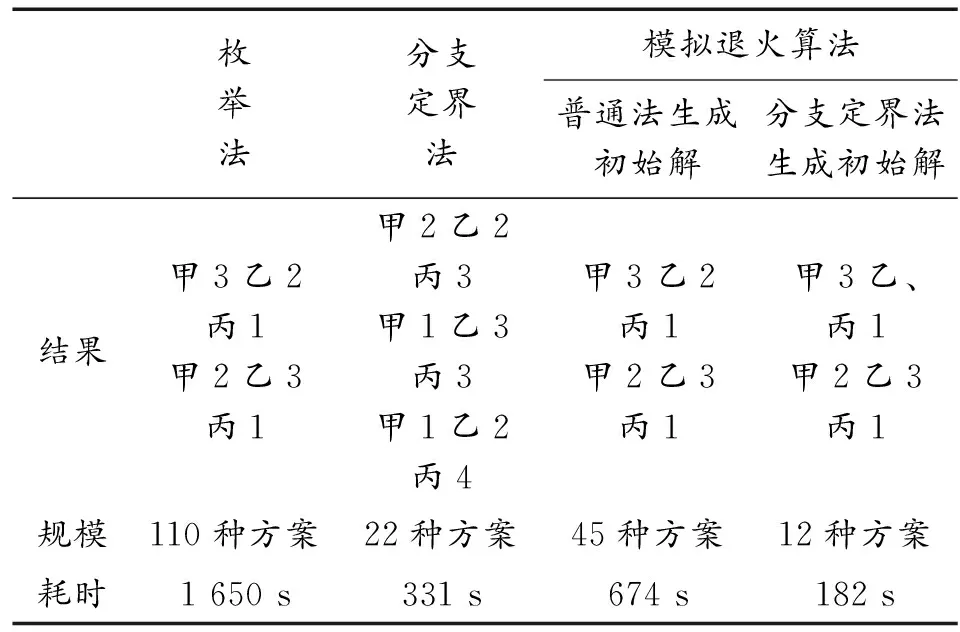
4 仿真算例及结果分析

5 结束语

