基于双线性对的踪迹属性计算可靠性分析∗

付浩

（长沙师范学院教育技术中心长沙410100）

基于双线性对的踪迹属性计算可靠性分析∗

付浩

（长沙师范学院教育技术中心长沙410100）

针对目前越来越复杂的安全协议，在建立计算可靠的安全协议符号分析方法的深入研究，提出了一种解决该问题的新方法，即踪迹属性的计算可靠性分析方法。关于踪迹属性的计算可靠性分析方法研究，在主动攻击者模型下，提出了计算可靠且支持双线性对、公钥加密、数字签名的安全协议符号模型，该模型明确指定双线性对实例生成器、加密算法和签名算法需要满足的安全假设，并证明了在满足这些安全假设的条件下，符号方法分析的踪迹属性蕴含计算方法分析的踪迹属性，这证明了该模型具有计算可靠性。

安全协议；计算可靠性；踪迹属性；双线性对

Class NumberTP391

1 引言

进入二十一世纪以来，随着互联网网络信息技术的飞速发展，信息网络的广泛应用已成为人们工作和生活不可或缺的一部分。计算机网络给人们生活带来巨大便利，同时也对网络上信息的安全保护提出了更高的要求。如果计算机网络的安全问题不能切实有效地解决，那么它的应用和发展必定会受到一定的影响。

安全协议是解决网络安全问题最有效的手段之一。构建安全网络环境一般采用密码技术的安全协议，安全协议的目标既是为了实现信息的加密传输，也是为解决网络中的安全问题，它的正确性和安全性对于网络安全极其重要。安全协议的形式化分析已有三十多年的历史，一直存在两类不同的方法：计算方法和符号方法。计算方法是在概率论和计算复杂性理论基础上的一种“归约”方法，其结果更具密码学可靠性。但是证明过程是高度创造性的手工数学式证明，这对于目前越来越复杂的安全协议，不仅证明本身越来越复杂，而且证明的正确性也越来越不容易。符号方法用形式化语言和符号推理对协议进行分析和验证，更容易实现自动化分析。但是由于对密码学原语和攻击者能力的理想建模，使得这类分析方法的肯定性结论往往并不直接具有现实意义，被认为没有真正建立起密码学的可靠性。目前，安全协议的设计与分析已经成为研究热点，并且也有多种形式化的方法来解决其中的问题。

Micciancio和Warinschi［1］针对使用公钥加密原语的双方协议，首次在主动攻击者模型下分析了踪迹属性的计算可靠性。当加密算法满足IND-CCA安全性时，每个计算踪迹都是某个符号踪迹在计算模型下的映射。该可靠性定理表明在给定条件下计算方法中攻击者的能力不比符号方法中攻击者的能力强。这也表示如果安全协议在符号模型下满足某符号踪迹属性，则在计算模型下也满足其对应计算踪迹属性。

本文将对经典Micciancio-Warinschi方法进行扩展，进一步描述基于双线性对的多参与者密钥交换协议，并优化攻击者模型，最终建立使用数字签名原语、公钥加密原语和双线性对的符号模型和计算模型；随后分析了符号迹和计算迹之间的对应关系，论证了符号模型下踪迹属性的计算可靠性。

2 符号模型

2.1 消息

在该符号模型中，协议交互消息通过符号表达式表示，称之为消息项，由参与者标识符和随机数经过密钥生成、连接、公钥加密、数字签名和模幂、双线性对运算等构建。

定义1消息

消息的语法可由如下BNF规则给出：

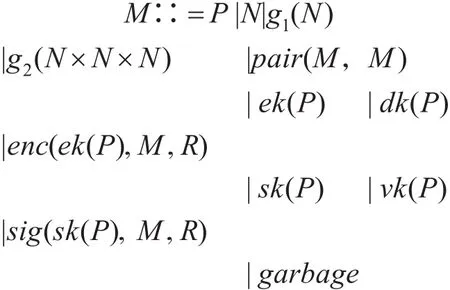
其中P表示协议参与者的身份标识符。N=NP∪NE表示协议参与者和攻击者产生的新鲜值。R=RP∪RE表示协议参与者和攻击者产生的随机数。g1(x)表示用新鲜值x生成的双线性对中加法循环群G1中的元素gx1。g2(x)表示x生成的双线性对中乘法循环群G2中的元素g2x。ek(pi)，dk(pi)，sk(pi)，vk(pi)分别表示参与者pi的加密密钥、解密密钥、签名密钥和签名验证密钥。pair(m1，m2)表示两个消息项m1和m2的连接。enc(ek(pi)，m，r)表示用密钥ek(pi)和随机值r加密消息m。sig(sk(pi)，m，r)表示用密钥sk(pi)和随机值r签名消息m。garbage表示攻击者产生的一些无效项。

定义2子项

项t，t′∈M，若下列条件之一满足：

如果项t为一个变量或一个常量，则t′=t；

如果t=f(t1，t2，…，tn)，则或者t′=t，或者存在ti，i∈{1，2，…，n}使得t′⊑ti，

则称子项关系t′⊑t成立。

定义3置换

置换σ为函数σ={x1→t1，…，xn→tn}，将变量xi置换为消息项ti。

2.2 协议

定义4协议

一个k方协议由k个不同角色组成，Π：i→Π(i)，i∈[k]。角色的并发执行称为协议的一次会话。角色形式化为协议会话中某个参与者执行的一组发送接收消息的动作序列，Π(i)= {(R1，Q1)，(R2，Q2)，…，(Rn，Qn)}，其中(Rj，Qj)∈Π(i)表示第i个角色在第j步接收消息Rj后计算Qj并发送。对于协议会话的发起者，R1为空；会话中某些角色的Qn也可能为空。但是，并不是所有协议都是有效的。

定义5有效协议

我们称协议Π有效：

当参与者数量的长度为l，协议中消息序列的长度为m，如果存在一个多项式p，使得l关于p(m)有界；

且对于协议会话角色i的消息序列Π(i)中的任何一个Qj，都存在一个多项式时间算法可计算。

2.3 攻击者模型

安全协议分析的符号模型假定攻击者控制着整个通信网络，所有参与者之间交互的消息都通过攻击者转发。攻击者能够观察所有消息，而且可以截获并伪造消息。通过允许攻击者选择某参与者集合并获得该集合中所有参与者的私钥来模拟攻击者攻陷某不可靠参与者集合［2］。

攻击者可以执行以下三类动作：

1）Corrupt(p1，…，pl)：攻击者攻破参与者{p1，…，pl}，获得其对应私钥；

2）new(i，p1，…，pk)：攻击者可以作为角色i与参与者{p1，…，pk}发起协议的新会话；

3）Send(sid，m)：攻击者可以在会话sid中发送消息m，参与者收到消息相应的更新状态，并向攻击者返回对消息m的响应。

攻击者的知识推理能力通过定义攻击者所能计算的所有消息来描述，即推演关系“├”。攻击者的知识包括攻击者的初始知识和从诚实参与者截获的所有消息，以及通过推演关系获得的所有消息。

定义6推演关系

推演关系“├”是满足下述条件的最小关系

1）若m∈S，则S├m，S├l；

2）若x∈{P，EK，VK，NC，DKC，SKC，NE}，则S├x；

3）S├garbage；

4）若S├ek(x)，S├m，r∈RE，则S├enc(ek(x)，m，r)，若S├enc(ek(x)，m，r)，S├dk(x)，则S├m，S├r；

5）若S├sk(x)，S├m，r∈RE，则S├sig(sk(x)，m，r)，若S├sig(sk(x)，m，r)，则S├verify(vk(x)，sig(sk(x)，m，r))。

定义7有效Dolev-Yao攻击者

若攻击者发送的每条消息都是其可推演的，则称此攻击者为有效Dolev-Yao攻击者。

2.4 符号迹

定义8符号迹

k方协议Π的符号踪迹ts是满足符号迁移规则的有穷全局状态序列［3］。

全局状态由一个三元组(Sid，f，S)组成，其中，Sid={(n，(p1，…，pk))}表示会话标识的有穷集合，n标识会话，pi表示会话n中角色i的参与者身份标识；函数f将每个会话标识sid映射到会话的当前局部状态，f(sid)=(i，σ，t，(p1，…，pk))，其中i表示会话sid中当前执行的角色，σ是一个将变量映射到符号消息的部分函数，t表示协议执行的当前位置；S表示攻击者已获得的知识集合。

协议的初始状态qI=(∅，∅，NE)。

3 计算模型

在计算模型中，协议的安全强度与协议安全参数η密切相关，新鲜值长度、密钥长度等参数的取值都与安全参数η［2］相关。协议消息为二进制位串，通过随机数生成、模幂、连接、公钥加密算法与数字签名算法得到。密码算法是协议安全性的基础，符号模型由于将密码算法抽象为确定的黑盒算法，丧失了计算可靠性。计算模型在使用密码算法时，将其作为具有标准安全属性和特殊属性的多项式时间内可计算函数使用［4］。

3.1 密码算法及安全性

公钥加密是使用比较广泛的加密算法之一。在公钥加密算法中，密钥是密钥对的形式出现。一个密钥对可分为公钥和私钥。密钥所有者将公钥进行公布，其他人可以通过所获得的公钥对数据进行加密。加密的数据可以通过该公钥所有者的私钥进行解密。

定义9公钥加密算法

公钥加密算法由三个关于安全参数η的多项式时间算法组成AE=(KG，E，D)。

密钥生成算法KG：根据给定安全参数η从密钥空间随机选择密钥对(ek，dk)并将其输出，η决定密钥长度。

加密算法E：根据随机硬币r，加密密钥ek和消息明文m，计算并输出密文c，记为Eek(m，r)。

解密算法D：根据解密密钥dk和密文c验证c的有效性，若有效则输出其解密明文，记为Ddk(c)，否则输出错误消息⊥。

并且，对任意的安全参数η，密钥(ek，dk)∈KG(h)，随机硬币r，若m是明文空间的消息，则Ddk(Eek(m，r))=m。

定义10非适应性不可区分选择密文攻击安全（IND-CCA安全）

对于任意安全参数η，任意概率多项式时间图灵机攻击者A的优势［5］

是η的可忽略函数，则称加密算法AE=(KG，E，D)满足IND-CCA安全。

定义11数字签名算法

数字签名算法Sig由三个关于安全参数η的多项式时间算法组成Sig=(KGs，S，V)。

密钥生成算法KGs：以1η为输入（η是安全参数），随机产生密钥对(sk，vk)，其中，sk为签名密钥，vk为验证密钥。

签名算法S：用给定签名密钥随机产生对给定消息的签名σ。

验证算法V：给定消息m、签名s及验证密钥vk，检验s是否是m对应于vk的正确签名。

定义12不可伪造性（UNF安全）

对任一数字签名方案(KGs，S，V)，在多项式时间内，如果适应性选择消息攻击者A可构造出一个能通过验证算法验证的指定签名的概率是可忽略的，则称该方案是UNF安全的［6］。

定义13双线性对

双线性对e：G1×G1→G2，其中G1为素数阶q加法循环群，G2为同样阶的乘法循环群，g1为G1中的生成元。

双线性对具有如下特点：

1）双线性：对于任意x，y∈Z*q，

2）非退化性：e(g1，g1)是G2的生成元，用g2表示，g2≠1G2。

3）可计算性：对于任意u，v∈G1，存在一种有效的算法计算e(u，v)。

双线性对实例生成器IG是一个概率多项式时间算法，给定安全参数η，输出五元组(q，G1，G2，g1，e)。

3.2 计算迹

在计算模型中，协议的描述同符号模型，但是交互的消息不再是代数项，而是二进制位串。因此对协议中每个角色的接收发送消息动作(Rj，Qj)∈Π(i)，需要析构接收消息Rj的对应位串，以及构造发送消息Qj的对应位串［7］。

在标识符为sid的会话中，接收消息位串m，给定变量到位串映射t，角色i的析构消息位串算法parsei，sid(m，Rj，τ)递归定义如下：

1）当Rj=x∈X，若m的类型与x不匹配，则中止；若τ(x)已定义且τ(x)=m，则返回τ(x)；若τ(x)≠m，表示不是期望接收的消息，中止；若t(x)未定义，则令τ(x):=m，返回t。

2）当Rj=ek(x)，若m不是加密公钥，则中止；否则令tagek(ek):=m。若m是参与者pi的加密公钥，且τ(x)未定义，则令τ(x):=tagagent(pi)，返回t；否则中止。

3）当Rj=sig(sk(pi)，Rj1，r)，若m不是签名，则中止；否则令tagsig(s，m′，vk):=m。令τ1= parsei，sid(tagvk(vk)，vk(pi)，τ),τ2=parsei，sid(m′，Rj1，t)，若映射关系τ1和τ2有冲突，中止；否则返回τ1∪τ2。

在标识符为sid的会话中，给定变量到位串映射t，角色i的构造消息位串算法construci，sid(Qj，t)递归定义如下：

1）当Qj=x∈N，若τ(x)已定义，则返回τ(x)；否则中止。

2）当Qj=ek(x)，若τ(x)未定义，中止；否则令tagagent(pj):=τ(x)。通过密钥生成算法得到加密密钥ek，返回tagek(ek)。

3）当Qj=dk(x)，若τ(x)未定义，中止；否则令tagagent(pj):=τ(x)。若pi≠pj，即角色i的参与者pi不拥有解密密钥，中止；否则通过密钥生成算法。

4）当Qj=sig(sk(x)，Qj1，r)，若τ(x)未定义，中止；否则令tagagent(pj):=τ(x)。若pi≠pj，中止；否则sk，vk为参与者pj的签名密钥和验证密钥，选择随机数r，递归计算m′=construci，sid(Qj1，t)，通过签名算法获得m=Ssk(m′，r)，并返回tagsig(m，m′，vk)。

定义14计算迹

k方协议Π的关于安全参数η和概率多项式时间攻击者A的计算踪迹(η)是满足以下给定算法的有穷全局状态序列［8］。

全局状态由一个三元组(Sid，g，C)组成，Sid表示会话标识的有穷集合，C表示已攻破的参与者，函数g将每个会话标识sid映射到会话sid的当前局部状态，形如(i，τ，t，(p1，…，pk))，i表示会话sid中当前执行的角色，τ是一个将变量映射到位串的部分函数，t表示协议执行的当前位置，pj表示角色j的参与者身份［9］。

协议的初始状态是qI=(∅，∅，∅)。攻击者被激活。

若攻击者输出corrupt(p1，…，pk)，则qI→(∅，∅，{p1，…，pk})，攻击者获得参与者p1，…，pk的解密密钥和签名密钥。

若攻击者A输出new(i，p1，…，pk)，则(Sid，g，C)→(Sid′，g′，C)。其中Sid′:=Sid∪{sid}，sid为攻击者新发起会话的标识。∀x∈Sid，g′(x):=g(x)。g′(sid):=(i，t，e，(p1，…，pk))，其中ε表示协议中角色i的执行序列，τ(Pj):=tagagent(pj)，j∈[k]，nj←{0，1}η，τ(Xj):=tagnonce(nj)。

若攻击者A输出send(sid，m)，则(Sid，g，C)→(Sid，g′，C)。此处sid∈Sid，但m可以是攻击者通过算法构造的任意位串。若x≠sid，g′(x):=g(x)。令(i，τ，t，(p1，…，pk)):=g(sid)，Rj为协议当前执行到t处时期望收到的消息，Qj为协议收到消息Rj后发送的消息，并且协议执行的当前位置转到t′。通过解构算法parse解构输入消息m，若m与Rj匹配成功，τ′:=parse(m，Rj，τ)，通过构造算法con⁃struct构造输出消息m′:=construct(Qj，τ′)。若parse和construct算法都成功，则g′(sid):= (i，τ′，t′，(p1，…，pk))，否则g′(sid):=g(sid)。

当攻击者输出其他消息，则计算迹终止。

协议Π的计算迹为ExeccΠ，A(η)={tr1…trn|((Sid1，g1，C1)(Sid2，g2，C2)…(Sidn+1，gn+1，Cn+1)使得(Sid1，g1，C1)(＜tr1＞(Sid2，g2，C2) (…(＜trn＞(Sidn+1，gn+1，Cn+1)}。

4 计算可靠性

定义15计算实例

令ts=(Sid1s，f1，S1)，…，(Sidms，fm，Sm)为符号踪迹，tc=(Sid1c，g1，C1)，…，(Sidnc，gn，Cn)为计算踪迹，则当满足下列条件时，称tc是ts的计算实例，符号表示为ts≼tc。

1）m=n；

2）∀l∈[n]，Sidls=Sidlc，Cl={p:dk(p)∈Sl}；

3）∀sid∈Sidls，令(i，σ，t，(p1，…，pk)):=fl(sid)，(j，t，s，(q1，…，qk)):=gl(sid)，存在消息符号表达式到位串的映射c使得t=c°σ，且i=j，t=s，(p1，…，pk)=(q1，…，qk)。

定理1计算可靠性定理

令k方协议Π使用的加密算法满足IND-CCA安全，签名算法满足UNF安全，双线性对实例生成器满足DBDH假设，则对于任意概率多项式时间攻击者A，存在可忽略函数ε(h)，使得

证明：

首先，构造位串m到消息表达式的单射函数cˉ:{0，1}*→M，将攻击者自己生成的所有随机数{0，1}*→R，新鲜值{0，1}*→NE，以及不可析构的垃圾消息{0，1}*→Garbage［10］。

若m是参与者身份标识符，则tagagent(p):=m，返回p。

若m是新鲜值，则在计算迹的状态序列中检测m是否是参与者p在会话sid中生成的，若是则返回np，sid，否则返回NE(m)。

若m是加密密钥，则tagek(ek):=m，ek对应的参与者为p，若不存在则返回ek(n)，否则返回ek(p)。若m是解密密钥，则tagdk(dk):=m，dk对应的参与者为p，若不存在则返回dk(n)，否则返回dk(p)。

若m是验证密钥，则tagvk(vk):=m，vk对应的参与者为p，若不存在则返回vk(n)，否则返回vk(p)。若m是签名密钥，则tagsk(sk):=m，sk对应的参与者为p，若不存在则返回sk(n)，否则返回sk(p)。

若m是群G1中的元素，则tagg1(g1):=m，返回g1(x)。

若m是群G2中的元素，则tagg2(g2):=m，返回g2(x)。

若m是对偶，则tagpair(m1，m2):=m，返回pair(cˉ(m1)，cˉ(m2))。

接下来，通过映射函数cˉ将计算迹tc=(Sid1，f1，C1)…(Sidn，fn，Cn)映射到符号迹cˉ(tc)=(Sid1，f1，S1)…(Sidn，fn，Sn)。令fl(sid)=(i，cˉ°τ，t，(p1，…，pk))，其中(i，τ，t，(p1，…，pk)):=gl(sid)，定义攻击者的知识集合：S1:=NE。若第l次迁移规则是Corrupt(p1，…，pk)，则Sl+1:=Sl∪{dk(pj)，sk(pj):j∈[k]}；若第l次迁移规则是new(i，p1，…，pk)，则Sl+1:=Sl；若第l次迁移规则是Send(sid，m)，攻击者收到响应消息为m′，则Sl+1:=Sl∈{cˉ(m′)}。

tc是ExeccΠ，A(η)的分布下的计算迹，下面证明cˉ(tc)以压倒性概率是有效的符号迹。若cˉ(tc)不是符号迹，则存在第l步迁移send(sid，m)，m不满足NE∪{dk(pj)，sk(pj):pj∈C}∪{cˉ(m′):m′Sl}├cˉ(m)。若cˉ(m)不可推演，则cˉ(m)中有某一子项T不可推演。

若T为解密密钥ek(p)，T不可推演则可以通过攻击者A来构造攻击者A′破坏加密算法的非适应性不可区分选择密文安全，因此攻击者发送m的概率是可以忽略不计的；

若T为签名密钥ek(p)，T不可推演则可以通过攻击者A来构造攻击者A′破坏签名算法的不可伪造安全，因此攻击者发送m的概率是可以忽略不计的。

综上所述，对于所有计算迹中攻击者发送的消息不满足NE∪{dk(pj)，sk(pj):pj∈C}∪{cˉ(m′):m′Sl}├cˉ(m)的概率是可忽略不计的，计算模型中攻击者的行为都符合符号模型下的假设。因此，cˉ(tc)以压倒性概率是有效的符号迹。又由于cˉ是单射，因此有部分函数c:=cˉ-1。若cˉ(tc)是符号迹，则cˉ(tc)≼ctc。因此

证毕。

5 结语

本文分析了踪迹属性的计算可靠性。具体包括：1）给出了支持公钥加密、数字签名以及双线性对的符号模型，定义了消息的符号表达式和多方协议的描述。2）给出了攻击者模型，并在主动攻击者模型下进行分析。3）定义了协议的符号迹和计算迹。4）证明了在满足一定的安全假设下给出的模型每个计算迹都是某个符号迹的计算实例，即计算方法中攻击者的能力不比符号方法中攻击者的能力强。

［1］Daniele Micciancio and BogdanWarinschi.Soundness of formal encryption in the presence of active adversaries［C］//Theory of Cryptography Conference（TCC'04）.Cam⁃bridge，MA，USA.Springer LNCS 2951，2014：133-151.

［2］Cortier V，Kremer S，Warinschi B.A survey of symbolic methods in computational analysis of cryptographic sys⁃tems［J］.Journal of Automated Reasoning，2015，46：225-259.

［3］Meng B.A Survey on Analysis of Selected Cryptographic Primitives and Security Protocols in Symbolic Model and Computational Model［J］.Information Technology Journal，2014，10（6）.

［4］Blanchet B.Security protocol verification：Symbolic and computational models［C］//Proceedings of the First inter⁃national conference on Principles of Security and Trust. Springer-Verlag，2015：3-29.

［5］Canetti R，Goldreich O，Halevi S.The random oracle meth⁃odology，revisited［J］.Journal of the ACM，2014，51（4）：557-594.

［6］Ran Canetti and Hugo Krawezyk.Analysis of key ex⁃change Protocols and their use for building secure chan⁃nels.In Birgit Pfitzmann，editor，EUROCRYPT，volume 2045 of Lecture Notes in Computer Science，Pages 453-474.Springer，2016.

［7］罗正钦.基于UC框架的安全协议形式化分析［D］.上海：硕士论文.上海交通大学，2013. LUO Zhengqin.Formal analysis of security protocols based on UC framework［D］.Shanghai：Master Thesis，Shanghai Jiaotong University，2013.

［8］李建欣，李先贤，卓继亮，等.SPA：新的高效安全协议分析系统［J］.计算机学报，2015，28（3）：209-318. LI Jianxin，LI Xianxian，ZHUO Jiliang，et al.SPA：new ef⁃ficient security protocol analysis system［J］.Journal of computers，2015，28（3）：209-318.

［9］李梦君，李舟军，陈火旺.SPVT：一个有效的安全协议验证工具［J］.软件学报，2015，17（4）：898-906. LI Mengjun，LI Zhoujun，CHEN Huowang.SPVT：an ef⁃fective security protocol verification tool［J］.Journal of software，2015，17（4）：898-898.

［10］张子剑，祝烈煌，王峰，等.计算可靠且高效的群组密钥协商协议符号化分析方法［J］.计算机学报，2014，35（4）：664-672. ZHANG Zijian，ZHU Liehuang，WANG Feng，et al.Cal⁃culation and reliable and efficient group key agreement protocol symbolic analysis method［J］.Journal of comput⁃er，2014，35（4）：664-672.

Reliability Analysis of Trace Properties Calculation Based on Bilinear Pairings

FU Hao
（Education Technology Center，Changsha Normal College，Changsha410100）

In this paper view of the present increasingly complex security protocols，the establishment of calculation and reli⁃able security protocol in-depth study of symbolic analysis method，this paper proposes a new method to solve the problem，namely the trace properties calculation of reliability analysis methods.Researching on trace properties calculation of reliability analysis methods，under the active attacker model，puts forward the calculation and reliable support for bilinear pairings，public-key en⁃cryption，digital signature safety protocol symbol model.This model explicitly specifies the double linear generator for instance，en⁃cryption and signature algorithm need to satisfy the safe assumption，and proves that under the condition of meeting these safe as⁃sumption，symbolic methods to analyze the trace attribute contains the calculation method for the analysis of trace attribute，which proves the reliability of the proposed model.

security protocols，calculate reliability，trace properties，bilinear pairings

TP391

10.3969/j.issn.1672-9722.2017.07.027

2017年1月7日，

2017年2月18日

国家自然科学基金青年科学基金项目（编号：41604117）资助。

付浩，男，硕士，助理工程师，研究方向：物联网、网络安全协议。