正交度对高精度二维转台测量精度的影响

王建永 张晨阳 赵文峰 崔世程

（北京空间机电研究所，北京 100094）

正交度对高精度二维转台测量精度的影响

王建永 张晨阳 赵文峰 崔世程

（北京空间机电研究所，北京 100094）

针对二维跟踪测量转台方位轴和俯仰轴正交度对角度测量精度的影响，基于球面三角计算方法和向量运算方法，文章分别推导获得转台不正交时角度测量误差的计算公式，分析上述公式获得正交度及其测量误差对转台测角精度的影响规律。结果表明，二维转台俯仰运动范围大于 10°时，转台方位轴和俯仰轴正交度对方位测角精度影响较大，对俯仰测角精度影响可忽略不计；转台测角精度对正交度的测量误差非常敏感，俯仰角为75°时，若正交度测量误差为3″，则方位角测量误差可达11.2″。基于此提出一种正交度分段拟合的修正方法可将正交度对测角精度的影响控制在4″以内。最后，针对性的介绍了转台旋转轴正交度的两种测量方法及其测量误差主要来源。研究结果对通用二维跟踪测量转台测角精度指标的合理分解具有一定的指导意义。

二维转台 轴系正交度 误差分析 测量方法 航天遥感

0 引言

随着航天事业的发展，星载高精度二维转台在空间角度测量领域的应用越发广泛，根据星载精密探测仪器在轨任务需要，需要配备能快速完成高精度指向和精确测角的星载高精度二维转台。因此转台的测角精度直接决定系统的总体性能和在轨任务实现[1-2]。

目前针对转台测角精度影响因素的研究主要集中在轴系跳动、测角元件精度、延时精度、转台控制精度等方面[3-5]：轴系跳动可通过控制加工和装配精度加以保证[6-8]；测角元件精度可通过选择高精度的光电编码器或旋转变压器得以解决[7-11]；延时精度通过采用高精度的晶振及配套电路得以实现；转台控制精度通过提升算法和控制系统鲁棒性得以提高[12-15]。但转台正交度对转台测角精度的研究相对较少。而星载用转台存在尺寸、质量约束，并且需要承受发射动力学环境、在轨空间温度交变、空间失重环境以及空间寿命可靠性等环境条件，使得星载用转台的正交度很难维持在2″以内。且由于任务需要，星载用转台的运动范围较大，使得正交度对转台测角精度的影响变得尤为不可忽略。

本文推导分析了转台测角精度与转台正交度的函数关系，分别研究了正交度及其测量误差对测角精度的影响规律，并提出了一种分段拟合的修正算法以进一步提高转台测角精度，有助于在通用二维转台研制过程中对转台测角精度指标进行合理分解。

1 正交度影响数学模型

1.1 影响机理分析

二维转台利用俯仰旋转轴（内框）和方位旋转轴（外框）根据右手螺旋定则建立目标测量坐标系，见图1。理想状态下，X、Y、Z三轴构成笛卡儿坐标系。但是由于零件加工误差和产品装配误差的叠加，造成二维转台俯仰轴和方位轴不正交（正交度定义为θ），即真实俯仰轴Y′与理想俯仰轴Y存在夹角θ，根据真实转台旋转轴系分别建立真实角度测量坐标系（O-X′Y′Z′）和理论测量坐标系（O-XYZ），即

在理想情况下（θ=0°），在O-XYZ坐标系中，OP对应的测量角度为（Az，H），在实际情况下，由于θ的存在，在O-X′Y′Z′坐标系中，OP的实际测量角度为（Az′，H′），即方位测角误差为δAz=Az-Az′，俯仰角测量误差为δH=H-H′。

1.2 误差模型推导

图2为测角指向示意图。由OP0旋转至OP存在两种路径：第一种为先完成方位轴旋转（由OP0旋转至OP1），再完成俯仰轴旋转（由OP1旋转至OP）；第二种为先完成俯仰轴旋转（由OP0旋转至OP2），再完成方位轴旋转（由 OP2旋转至 OP）。因此，转台测量误差公式可采用两种推导方法：第一种路径采用球面三角法进行误差模型推导，而第二种路径则采用直角坐标系向量法进行误差模型推导。

1.2.1 球面三角法

图3为球面直角ΔABC，其中O为球心，∠A为ΔAOB与ΔABC的夹角（直角），∠B为ΔAOB与 ΔBOC的夹角，∠C为ΔAOC与ΔBOC的夹角，a，b，c分别为弧段对应的球心角，由球面三角理论可知，已知任意两个角度，根据式（2），即可求出其余角度[16]。

如图2所示，OP0通过旋转到达OP指向位置，在转台理论测量坐标系里，先绕Z轴旋转Az，再绕Y轴旋转H，即在球面上弧段对应的球心角为弧段对应的球心角为H，Y轴垂直于Z（Z′）轴，则在真实测量坐标系中，由于Y′轴与Y轴偏差了θ，实际需要先绕Z′轴（即Z轴）旋转Az′，再绕Y′轴旋转H′，即在球面上弧段对应的球心角为Az′，弧段对应的球心角为H′，由于Y轴与Z（Z′）轴夹角为γ（θ的余角），则弧段与弧段的夹角为γ，根据以上分析，建立球面三角△PP1P1′，根据式（2）可得δAz和δH的误差公式，其中H和Az满足右手螺旋定则，以绕旋转轴逆时针旋转为正。

1.2.2 直角坐标系向量法

图 4为旋转与角位置对应关系图。在真实二维转台测量坐标系中，先完成俯仰轴旋转，即OP0绕Y′轴旋转H′到达OP2，再绕Z（Z′）轴旋转Az′到达 OP，即在真实测量坐标系中 OP的角度为（Az′，H′）；而在理论二维转台测量坐标系中，OP0绕Y轴旋转H到达OP2′，再绕Z（Z′）轴旋转Az到达OP，即在理论测量坐标系中OP的角度为（Az，H），即方位测角误差为δAz= β- =Az-Az′，俯仰角测量误差为 δH=H-H′。由于 OP2、OP2′和OP均为OP0通过旋转产生。定义OP0为单位向量。图4中i、j、j′、k分别为X轴、Y轴、Y′轴和Z轴单位向量。

根据旋转关系，即OP2（对应向量简化为p2）与OP0的夹角为H′，OP2与Y′轴垂直。定义P点在O-XYZ坐标系中的坐标为（x，y，z），则P2点在O-XYZ坐标系中的坐标为（x′，y′，z）。由Y′轴位于ZOY平面里，且Y′轴与Y轴夹角为θ，即j在O-XYZ坐标系中坐标为（0，cosθ，sinθ），可得出

对比式（3）、式（4）与式（9）、式（10），基于两种计算方法用不同的优先旋转次序推导获得的误差计算公式是相同的。通过直角坐标系向量法的计算过程可知，沿方位轴（外框轴）的旋转不会引入测角误差，沿俯仰轴（内框轴）的旋转会产生俯仰测角误差和方位测角误差。

2 正交度影响数值分析

2.1 正交度对测角精度影响数值分析

针对某转台俯仰运动范围为[-30°，75°]，实测转台正交度为50″，通过式（9）、式（10）可计算出转台的方位角和俯仰角测量误差随俯仰角的变化曲线，如图5所示，转台俯仰角越大，则方位角和俯仰角测量误差越大。在75°时，方位角测量误差为-186.6″，而俯仰角误差仅为-0.02″，由此可得：正交度对方位角测量误差影响较大；对俯仰角测量误差极小，可忽略。

2.2 正交度测量误差敏感性数值分析

根据 2.1节的分析可知，在俯仰角较大时，正交度产生的方位测角误差较大，而俯仰测角误差则可以忽略不计。对式（9）进行微分，则

式（11）中正交度θ为小量，sin2θ≪1可忽略不计。转台俯仰测角误差dH′也为小量，sindHθ′为无穷小，可忽略不计。因此方位测角误差仅与转台俯仰角H′、正交度测量误差dθ′相关。

取正交度θ为50″，当转台运动俯仰角H′变化范围为[0°，75°]，正交度测量误差变化范围为[0″,15″]时，方位测角精度变化如图6（a）所示；当正交度测量误差取定值15″时，方位测角精度只与俯仰角（H′）变化相关，对应关系曲线如图6（b）所示；当转台俯仰角取定值75°时，方位测角精度只与正交度测量误差（H′）的变化相关，对应关系曲线如图6（c）所示。图6（a）对应的数据如表1所示。从图6和表1可知，当转台俯仰角较大时（俯仰角≥10°），方位测角精度对正交度测量误差非常敏感，例如，俯仰角为75°时，正交度测量误差在3″时，方位测角误差达11.2″。因此对于俯仰运动范围较大且测角精度要求较高的二维转台，则选择与测角精度相匹配的高精度正交度测量方法是极其必要的。

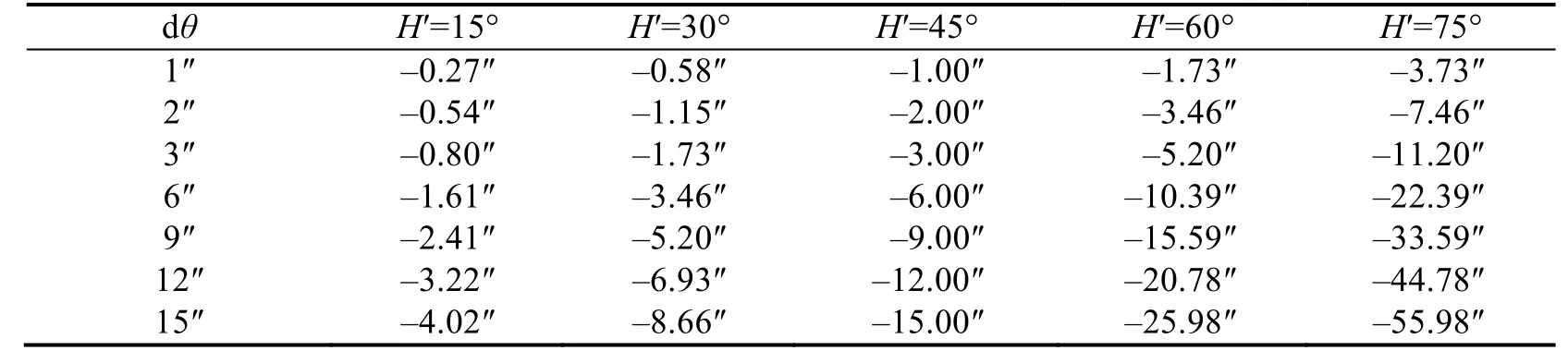
表1 正交度测量误差和转台俯仰角对方位测角精度关系表Tab.1 the relationship between the orthogonality measuring error and the azimuth angle measuring precision under different pitch angles

3 正交度修正方法

由上可知，转台正交度及其测量误差对方位测角精度影响较大，为提高二维转台的测角精度，必须对转台的正交度进行修正。二维指向机构的控制系统通常采用FPGA+DSP的信号处理系统，为减小计算量同时又能保证修正后的测角精度，本文提出一种采用分段函数线性拟合方法，取正交度测量值为 50″时，对式（9）分别在H′为0°、43°、58°、66°、71°、74°时进行一阶泰勒展开，展开后的分段拟合函数如式（12）所示（计算时 H′单位为 rad），考虑到修正时算法的稳定性，在满足修正精度（为测角精度的0.1倍）的情况下，在两个分段函数设置重叠区域。

分段拟合方位测角误差曲线如图7（a）所示，原始方位测角误差曲线如图7（b）所示，拟合误差曲线如图7（c）所示，由图可知，通过分段拟合修正，测角误差可以控制在3.6″。考虑到星载转台控制器用DSP资源余量和修正精度要求，选用高阶分段函数进行修正可以有效提高修正精度。

4 转台正交度测量方法

由上文分析可知，二维转台测量精度受正交度影响较大，且对正交度的测量精度非常敏感。但是，不同的正交度测量方法对应的测量误差也不同，这直接影响了二维转台的测量精度。因此，采用合适的正交度测量方法十分必要。本文有针对性介绍两种测量方法：接触式测量方法和非接触式光学测量方法。

（1）接触式测量法[16-18]

接触式测量法采用基准圆柱和三坐标测量仪配合完成正交度测量，需要转台方位轴（外环轴）运动范围不小于180°，俯仰轴（内环轴）旋转范围360°，通过计算方位角旋转180°前后的基准圆柱旋转中心的跳动值计算出正交度。本方法测量精度与基准圆柱和三坐标测量仪的精度密切相关，具体计算可见文献[18]。

（2）非接触式光学测量法[19-20]

光学测量法采用平面反射镜加自准直仪（或经纬仪）完成测量，需要转台方位轴（外环轴）运动范围不小于180°，俯仰轴（内环轴）运动范围360°，先在俯仰轴两端粘贴平面反射镜，并将平面反射镜与轴线调整垂直，测试时，先将外环轴旋转至0°，旋转中环轴，利用反射镜1间隔45°共测量8组数，可计算出外环轴为0°时的中环轴旋转轴线，再将外环轴旋转至180°，采用同样方法，利用反射镜2在中环轴同样的角度测量8组数，计算出外环轴为180°时的中环轴旋转轴线，将中环轴相同角度数据之差的一半中的最大值即为两轴正交度（共 4组数），具体测量方法和数据处理方法详见文献[19]。本测量方法精度较高，要注意两点：1）平面反射镜要与旋转轴线垂直；2）如果正交度测量值较大，必要时加密测量间隔，以减小测量误差。

5 结束语

本文深入分析了高精度二维转台正交度对测角精度的影响，给出了正交度对测角精度的影响公式、正交度测量误差敏感度公式及相应的误差修正公式，基于误差公式进一步分析了正交度对测角精度的影响，正交度测量误差对测角精度的影响以及正交度的修正对测角精度的影响，得出以下结论：

1）在俯仰角较大（大于10°）时，正交度误差对方位角测量精度影响较大，正交度为50″时，在俯仰角为75°时，产生的方位角测量误差为-186.6″；

2）正交度对俯仰角测量精度影响较小，俯仰角为 75°时，产生的俯仰角测量误差为-0.02″，可忽略不计；

3）方位角测量精度对正交度测量误差比较敏感，当俯仰角为75°时，正交度测量误差为3″时，产生的方位角测量误差为11.2″；

4）正交度对方位角测量精度的影响可以通过分段函数线型拟合方式进行修正，修正后正交度误差对测角精度的影响可以控制在4″以内。

References)

[1]杜俊峰, 张孟伟, 张晓明. 光电经纬仪测角精度分析[J]. 应用光学, 2012, 33(3)： 466-473. DU Junfeng, ZHANG Mengwei, ZHANG Xiaoming. Angle Measurement Accuracy of Photoelectric Theodolite[J]. Journal of Applied Optics, 2012, 33(3)： 466-473. (in Chinese)

[2]王家骐, 金光, 颜昌翔. 机载光电跟踪测量设备的目标定位误差分析[J]. 光学精密工程, 2005, 13(2)： 105-116. WANG Jiaqi, JIN Guang, YAN Changxiang. Orientation Error Analysis of Airborne Opto-electric Tracking and Measuring Device[J]. Optics and Precision Engineering, 2005, 13 (2)： 105-116. (in Chinese)

[3]杜俊峰, 李正周. GD-220光电经纬仪轴系的精度分析[J]. 光学精密工程, 2002, 10(4)： 416-419.DU Junfeng, LI Zhengzhou. Analysis of the Axial Accuracy of the GD-220 Photoelectric Theodolite[J]. Optics and Precision Engineering, 2002, 10(4)： 416-419. (in Chinese)

[4]李岩, 范大鹏. 光电稳定机构指向误差建模与敏感度分析[J]. 国防科技大学学报, 2008, 30(1)： 104-109. LI Yan, FAN Dapeng. Development of Pointing Error and Sensitivity Analysis of Opto-electrical Stabilization Mechanism[J]. Journal of National University of Defense Technology, 2008, 30(1)： 104-109. (in Chinese)

[5]曲智勇, 姚郁. 仿真转台误差分析及误差建模[J]. 计算机仿真, 2006, 23(3)： 301-304. QU Zhiyong, YAO Yu. Error Analysis and Error Modeling of Simulation Turntable[J]. Computer Simulation, 2006, 23(3)：301-304. (in Chinese)

[6]李婧, 康建兵. 闭环轴角解算误差分析及精度补偿方法[J]. 航天返回与遥感, 2014, 35(1)： 97-102. LI Jing, KANG Jianbing. Analysis and Compensation of Position Error Based on Loop Tracking Resolver-to-digital Converter[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1)： 97-102. (in Chinese)

[7]KIFIDENA V S B, FERREIRA P M. Kinematic Modeling of Quasistatic Errors of Three-axis Machining Centers[J]. Int J Machine Tools ＆ Manufacturing, 1994, 34(1)： 85-100.

[8]王涛, 朱明超, 訚胜利, 等. 稳定平台轴系精度对视轴指向误差的影响分析[J]. 红外与激光工程, 2011, 40(11)： 2265-2269. WANG Tao, ZHU Mingchao, YIN Shengli, et al. Analysis of LOS Pointing Error Derived from Precision of Shafting in Stabilization Mechanism[J]. Infrared and Laser Engineering, 2011, 40(11)： 2265-2269. (in Chinese)

[9]曹艳波, 艾华. 编码器轴系晃动对测角精度影响分析[J]. 光学仪器, 2016, 38(4)： 297-330. CAO Yanbo, AI Hua. Impact Analysis of the Spindle Rotation Error onto the Angular Measurement Precision of Photoelectric Encoders[J]. Optical Instruments, 2016, 38(4)： 297-330. (in Chinese)

[10]刘永江. 基于旋转变压器的位置检测方法及其应用[D]. 武汉： 华中科技大学, 2003. LIU Yongjiang. The Method and Application of Measurement of Position Based on Resolver-to-digital Converter[D]. Wuhan： Huazhong University of Science and Technology, 2003. (in Chinese)

[11]张京娟. 一种新型的旋转变压器测角误差标定技术[J]. 仪器仪表学报, 2010, 31(1)： 149-152. ZHANG Jingjuan. Novel Method of Calibrating the Angle-measurement Error of Resolver[J]. Chinese Journal of Scientific Instrument, 2010, 31(1)： 149-152. (in Chinese)

[12]肖龙, 杨佩君, 汤恩生. 基于软件锁相环的电机速度控制系统[J]. 航天返回与遥感, 2006, 27(3)： 41-46. XIAO Long, YANG Peijun, TANG Ensheng. The Velocity Control System of Electromotor Based on the Software Phaselocked Loop[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(3)： 41-46. (in Chinese)

[13]WAN Jiuqing. The Analysis and Design of High-speed Brushless Resolver Plus R/D Converter Shaft-angle Measurement System[J]. Electrical Machines and Systems, 2001, 11(1)： 10-16.

[14]肖龙, 汤恩生. 电机控制系统PID参数的遗传算法优化[J]. 航天返回与遥感, 2006, 27(2)： 34-37. XIAO Long, TANG Ensheng. The Optimizition of Genetic Algorithms for the PID Parameters of Motor Controller System[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(2)： 34-37. (in Chinese)

[15]HANSELMAN D C. Resolver Signal Requirements for High Accuracy Resolver-to-digital Conversion[J]. Industrial Electronics, IEEE Transactions on, 1990, 37(6)： 30-31.

[16]彭成荣. 航天器总体设计[M]. 北京： 中国科学技术出版社, 2011： 204-205. PENG Chengrong. System Design for Spacecraft[M]. Beijing： Science and Technology of China Press, 2011： 204-205. (in Chinese)

[17]任顺清, 陈希军, 袭建军. 三轴转台垂直度误差的测试与分离技术[J]. 计量技术, 2002(5)： 6-9. REN Shunqing, CHEN Xijun, XI Jianjun. The Measurement and Seperation of Vertical Error for Three-axis Turntable[J]. Measurement Technique, 2002(5)： 6-9. (in Chinese)

[18]王玉田. 三轴转台轴线垂直度的测试方法[J]. 计测技术, 2014, 34(1)： 42-44. WANG Yutian. The Method of Measuring Perpendicularities of Three-axis Turntable[J]. Metrology & Measurement Technology, 2014, 34(1)： 42-44. (in Chinese)

[19]贾宏进, 秦石乔, 胡浩军, 等. 轴系倾角回转误差与垂直度测量方法[J]. 计量技术, 2008(11)： 25-28. JIA Hongjin, QIN Shiqiao, HU Haojun, et al. The Measurement Method of the Wobble Error and Vertical Shaft[J]. Measurement Technique, 2008(11)： 25-28. (in Chinese)

[20]国防科学技术工业委员会. 惯性技术测试设备主要性能试验方法： GJB 1801-93[S]. 北京： 国防科工委军标发行部, 1994. COSTIND. Testing Methods of Major Performance for Test Equipments of Inertial Technology： GJB 1801-93 [S]. Beijing：Military Standard Press of Commission of Science Technology and Industry for National Defense, 1994. (in Chinese)

Effects of Orthogonality on the Measurement Precision of High-accuracy Two-dimensional Turntable

WANG Jianyong ZHANG Chenyang ZHAO Wenfeng CUI Shicheng
（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Considering the influence of orthogonality between azimuth axis and pitch axis on the angle measuring precision of two-dimensional tracking turntable, the formula of angle measuring error is derived based on the spherical triangle method and vector method respectively, when the azimuth axis and pitch axis of turntable is non-orthogonal. The effects of the orthogonality and its measuring error on the angle measuring precision are obtained from the formula. Results shows that when the motion range of the turntable is wider than 10°, the orthogonality between the azimuth axis and pitch axis has great effects on the measuring precision of the azimuth angle, but little effects on the pitch angle. Further results shows that the angle measuring precision is quite sensitive to the orthogonality measuring error. When the pitching angle is 75° and the orthogonality measuring error is 3″, the azimuth angle error can reach to 11.2″. Then an orthogonality segmented fitting method is proposed, which can control the angle measuring precision within 4″. Finally, two kinds of revolving axes orthogonality measuring methods and their main error source are summarized. These results have some instructional value for the analysis on the angle measuring precision of the general two-dimensional tracking turntable.

two-dimensional turntable; axes orthogonality; error analysis; measuring method; space remote sensing

V423.6

A

1009-8518(2017)03-0094-08

10.3969/j.issn.1009-8518.2017.03.011

王建永，男，1985年生，2010年获中国空间技术研究院光学工程专业硕士学位，工程师。研究方向为空间光机结构总体设计。E-mail：719920772@qq.com。

（编辑：王丽霞）

2017-02-09

国家重大科技专项工程