某水电站边坡降雨入渗力学特性及稳定性分析
徐 俊
(江苏省江都水利工程管理处,江苏 扬州 225200)
工程勘察
某水电站边坡降雨入渗力学特性及稳定性分析
徐 俊
(江苏省江都水利工程管理处,江苏 扬州 225200)
降雨对边坡稳定性及其失稳破坏有着重要影响,基于某水电站的工程地质参数,建立有限元模型,通过Abaqus对雨水入渗的瞬态渗流对边坡力学特性的影响进行建模与计算,认为静水压力随深度线性增加,建立CPE4P网格进行计算,对其渗透率、孔压、横纵向位移、偏应力、塑性应变及应力路径等作了分析,得出一系列降雨入渗作用下应力、应变及稳定性相关结论。
降雨;渗流;ABAQUS;失稳;边坡;塑性区
某水电站坝址处降雨频发,降雨对水电站边坡的稳定性造成了严重影响,土体的抗剪强度等力学参数会随着降雨的作用而降低[1],空隙水的压力会随着地下水位的抬高而升高[2-3],进而造成稳定性的下降[4]。除此之外,高强度、长时间的降雨会导致暂态饱和区的出现,以此导致空隙水压力的升高。基于此,有必要对雨水入渗情况下瞬态渗流影响下的边坡应力、应变等力学特性进行研究。
降雨入渗作为—种典型的非饱和流固耦合现象,目前已有较多学者对降雨入渗进行了研究,取得了较多成果[5-10]。但研究领域多在降雨入渗的影响因素、滑坡、初始含水率、稳定性等层面上,而基于多参数、多指标的综合分析研究较少,该文从数值模拟角度出发,土体参数取自于水电站,全面对渗透率、孔压、横纵向位移、偏应力、塑性应变及应力路径等进行了分析,以此更好地为降雨入渗对边坡的稳定性研究作参考与支持。
1 降雨入渗计算力学原理及边界条件
1.1 计算原理
土体材料的渗透系数与基质吸力关系如式(1):
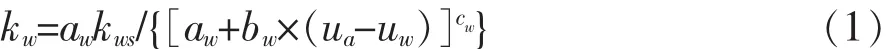
式中 kw为土体饱和时的渗透系数,取5.0×10-6m/s(0.018m/h);uw和ua为土体中的水压力、气压,因坡面与大气接触的原因,式中取为0。aw、bw和cw为材料系
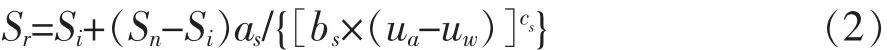
式中 Sr为饱和度;Si为残余饱和度,取0.08;Sn为最大饱和度, 取1;as、bs和cs为材料系数, 分别取1,5.0×10-5,3.5。
值得注意的是,ABAQUS中,有效应力的定义为σ′=σ-(χuw+(1-χ)ua),χ取为饱和度Sr,将ua赋值为0,采用基于有效应力的本构关系,该本构重点体现了基质吸力对模型的影响,这与反映黏聚力的强度本构具有较大差异。
1.2 边界条件
降雨入渗的物理过程十分复杂,Larson与Mein研究发现,通过土壤允许的入渗容量fp,降雨强度q及水力传导系kws数参数,可以揭示出降雨入渗行为。
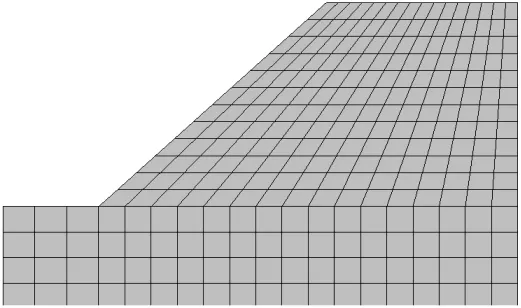
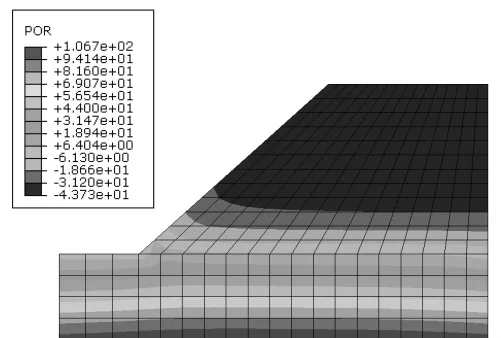
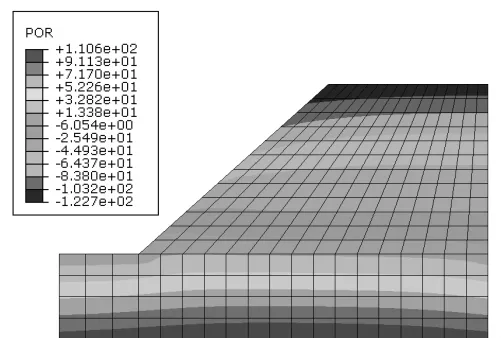
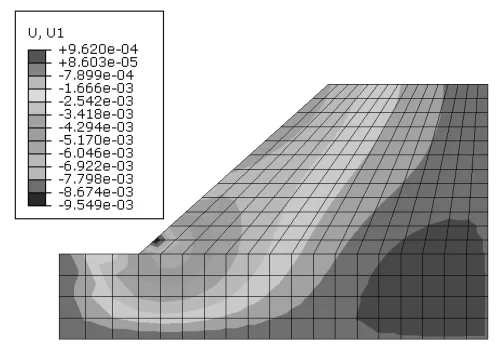
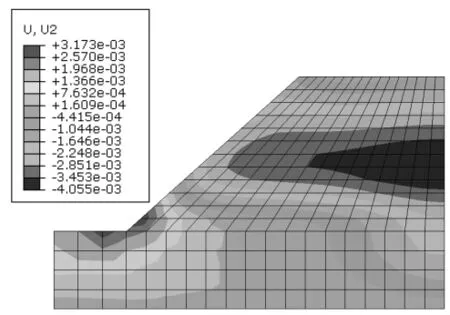
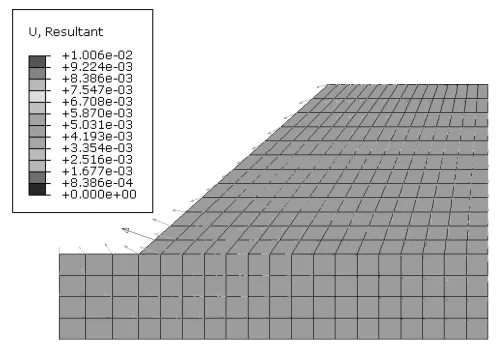
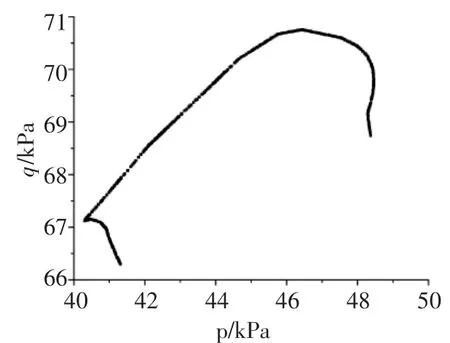
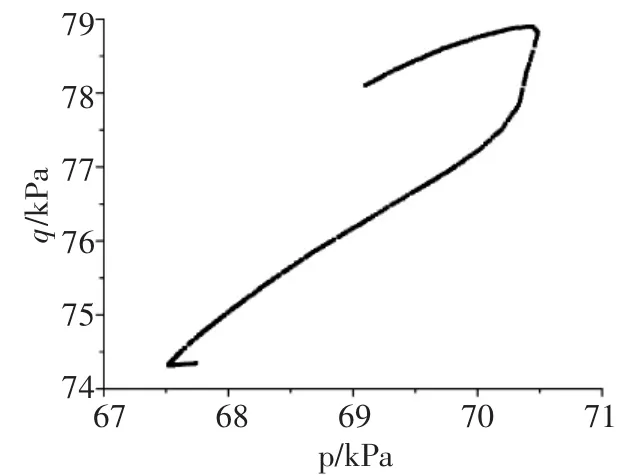
1.2.1 当q 地表径流在该情况下不会发生,降雨完全入渗至边坡,水的入渗率是不变的。 1.2.2 当fp>q>kws 雨水在该情况下全部入渗,随着入渗度的不断增加,fp不断减小,但降雨强度还未超过允许容量,因此,入渗率并不会出现降低的情况,其仍具有较高的数值。该情况时,坡面为流量边界。 1.2.3 当q>fp 降雨强度已超过土壤入渗容量,会出现部分降雨不入渗,而形成地表径流的情况。该情况中,坡面上的土体为饱和状态的土体,当达到入渗容量后,降雨将不断下降。 本文考虑fp>q>kws情况,降雨边界函数用降雨强度(单位流通量)来表示,同时,不考虑地表积水的情况,使分析区域顶面均受到降雨作用,其设置入渗强度和持续时间分别为20mm/h,66h。数,文中分别取1000,0.01,1.7。 饱和度随基质吸力的关系如式(2): 本文所建立的边坡模型即来自该水电站边坡,降雨入渗的模型参数来自于某水电站土体的实测参数,为了便于研究,将其简化成理想边坡,该边坡(坡角40°,坡高30m)力学参数如表1。 表1 水电站土体参数 基于降雨入渗计算力学原理及边界条件的选择,进行有限元模型的建立,所建立的有限元模型如图1。其element type选择为CPE4P,渗透系数随饱和度及基质吸力随饱和度的变化可根据式(1)和式(2)得到。 图1 有限元网格模型 其中,利用distribution定义孔压边界条件,在左、右两侧水位以下的边界上设置随深度线性增加的静水压力孔,按照式(3)进行设置。 式中 p为静水孔压力(Pa);Y为深度(m)。 分析步长时间为72h,以0.1作为初始时间增量步,将孔压设定为沿深度线性关系增加,降雨强度的时程赋值曲线Amp-1如表2。 表2 时间和幅值大小关系 对研究坡顶区域的降雨入渗边界条件进行设置,嵌入有效应力有限元文件,即可进行该模型的降雨入渗有限元分析。 在降雨入渗发生后,46,72h的孔压等值线云图如图2、图3。由图可知,孔压的分布云图与初始状态发生显著差异,在坡顶部范围以下的吸力区发生范围减小的现象,基质吸力参数较初始状态减小,随着降雨时间的增加,法向状态延长,饱和度也随之增大,孔隙水压力参数也随之增大。 图2 降雨46h后孔压云图 图3 降雨72h后孔压云图 随着降雨时间的增加,浅层土体的基质吸力不断减小甚至消失。而随着降雨减少直至停止,在时间不断延长的情况下,饱和度出现逐渐减小的情况,孔隙水压力也随之逐渐减小,土体浅层的基质吸力出现逐渐增加的情况。 降雨发生72h后的水平位移及沉降的等值线云图如图4与图5。由此可知,发生在坡脚的最大水平位移是9.55mm,边坡的中部发生最大沉降现象,沉降位移是4.06mm。由于初始设置的分布条件,导致坡顶没有出现最大抗降。 图4 降雨72h后的水平位移 图5 降雨72h后的沉陷 对坡顶进行单独分析,当降雨入渗发生后,吸力出现降低情况,孔压出现增加情况,有效应力出现减小情况,发生了卸裁回弹现象。除此之外,降雨入渗不断持续,使得土体容重和含水率增加,进而使得沉降和应力均出现增加现象。 降雨72h后的位移矢量如图6。可以看出,降雨入渗发生后,边坡出现明显滑动变形趋势,由此可知,边坡稳定性逐渐变低。 图6 降雨72h后的位移矢量 降雨入渗23h及72h后的等效塑性应变云图如图7和图8。可以看出,坡脚浅层由于降雨入渗作用首先出现塑性区,且塑性区沿坡面会不断地向上扩展。 图7 降雨入渗23h的等效塑性应变 图8 降雨入渗72h的等效塑性应变 选取塑性区中心点,等效塑性应变时程曲线如图9。可以看出,当t=20h时,塑性区出现在坡脚,随后降雨入渗时间的快速增加,当时间增加到50h后,降雨情况开始减小,此后,塑性区便不再向后扩展,等效塑性应变随之也不再增加,保持稳定不变。 图9 塑性中心单元等效塑性应变时程 利用ABAQUS提供的combine函数,绘出塑性区中心点和非塑性区中心点的有效应力路径如图10和图11。 图10 塑性中心单元有效应力路径曲线 图11 非塑性区单元有效应力路径曲线 由图10和图11可知,塑性中心单元和非塑性区中心单元的有效应力路径明显出现了不同的力学特征,对于出现在坡脚的塑性中心单元,如图10,由于降雨入渗,孔压开始增加,有效平均应力出现减小的情况,而减小到一定阈值后,有效应力路径表现出屈服现象,其处于屈服面位置,此时,应力路径向左下方逐渐下移,其沿着摩尔库仑强度包线形成的屈服面朝左下方移动,当降雨量减小后,移动停止,此时,吸力开始增加,孔压开始减小,在有效应力开始增大后,起逐渐远离屈服面。 而对于非塑性单元,如图11,其处于土方内部,上方的单元吸水后容重增加,导致塑性区单元的平均有效应力和偏应力都是增加的,直至降雨的后期,接近降雨结束时平均有效应力和偏应力都有所下降,即降雨入渗作用下主要是边坡浅层可能会出现失稳现象,该区域具有较高的失稳倾向性。 基于某水电站边坡的力学参数,通过ABAQUS对边坡降雨入渗现象进行了非饱和流固耦合分析,得出在降雨入渗的作用下,位移矢量图表明,边坡有明显的滑动变形的趋势,边坡稳定性由此逐渐降低,坡脚浅层会首先出现塑性区,并沿着坡面不断向上扩展,塑性点和非塑性点的有效应力路径表现出了不同的特征。 [1]王英豪.利用赤平极射投影法评价岩质边坡稳定性[J].水科学与工程技术,2011(6):57-59. [2]汪仕旭.降雨入渗对边坡稳定性的影响[D].广州:广东工业大学,2011. [3]曾耀.水库库岸老滑坡复活过程中地下水作用机制研究[D].武汉:中国地质大学,2010. [4]季洪涛.基于突变理论的土石坝坝坡安全稳定分析[J].水利建设与管理,2015(12):24-34. [5]张家明.植被发育斜坡非饱和带土体大孔隙对降雨入渗影响研究[D].昆明:昆明理工大学,2013. [6]周家文,徐卫亚,邓俊晔,等.降雨入渗条件下边坡的稳定性分析[J].水利学报,2008,39(9):1066-1073. [7]蒋中明,熊小虎,曾铃.基于FLAC~(3D)平台的边坡非饱和降雨入渗分析[J].岩土力学,2014,35(3):855-861. [8]陈洪松,邵明安,王克林.土壤初始含水率对坡面降雨入渗及土壤水分再分布的影响[J].农业工程学报,2006,25(1):44-47. [9]朱伟,陈学东,钟小春.降雨入渗规律的实测与分析[J].岩土力学,2006,27(11):1873-1879. [10]王协群,张有祥,邹维列,等.降雨入渗条件下非饱和路堤变形与边坡的稳定数值模拟[J].岩土力学,2010,31(11):3640-3644. (责任编辑:尹健婷) The numerical simulation of rainfall infiltration in slope on stress strain and stability characteristics in a hydropower station XU Jun The rainfall will affect the mechanical parameters of soil, based on Abaqus, the stress and strain of slope on rainwater infiltration effect is studied.An ideal slope is regarded as a case for modeling and calculation without considering the effect of rainfall water, and the hydro-static pressure increases linearly with depth, the CPE4P grid is established to calculated.The permeability, pore pressure, horizontal and vertical displacement, deviatoric stress, plastic strain and stress path are analyzed on post-processing,the instability phenomenon may appear on the shallow slope because of the effect of rainfall infiltration. rainfall; seepage; ABAQUS; instability; slope; plastic zone TU457 B 1672-9900(2017)03-0001-04 2017-04-21 徐 俊(1988-),男(汉族),江苏扬州人,本科,主要从事边坡稳定性方面的研究,(Tel)13813151027。2 降雨入渗模型的建立与求解



3 降雨入渗后的结果分析



4 结语
(Jiangdu Water Conservancy Project Management Office, Yangzhou 225200,China)

