温稠密物质物态方程的理论研究

马桂存张其黎 宋红州 李琼 朱希睿 孟续军

(北京应用物理与计算数学研究所,北京 100089)(2016年11月23日收到;2016年12月26日收到修改稿)

专题:高压下物质的新结构与新性质研究进展

温稠密物质物态方程的理论研究

马桂存†张其黎 宋红州 李琼 朱希睿 孟续军

(北京应用物理与计算数学研究所,北京 100089)(2016年11月23日收到;2016年12月26日收到修改稿)

本文详细地介绍了温稠密物质物态方程的理论模型,其中包括液体变分微扰理论、化学图像模型、离化电离平衡模型、平均原子模型和INFERNO模型;给出了混合物物态方程的计算方法;对第一原理分子动力学和量子蒙特卡罗方法进行了介绍;对一些典型材料(如氢、氘、氦、氙、金、钨等)在温稠密区的物态方程进行了计算和总结;分析了离解、电离效应对物态方程的影响.

温稠密物质,物态方程,等离子体

1 引 言

材料的物态方程是反映物质的压强、密度、温度之间的函数关系的方程[1].它在工程和科学技术中有着广泛的应用背景,如天体物理中的恒星构造、地球物理中的地核运动以及核聚变等领域中都需要知道材料的物态方程.在恒星体的内部(如太阳以及银河系中的其他类星体中),其物质的状态实际上是一种高温、高密度的等离子体状态.地球的内核实际上也是一种熔融的温稠密的等离子体态.

随着科学技术的快速发展,目前人们能够在实验室中实现材料的高温高压状态,如激光惯性约束聚变和磁约束聚变.美国的国家点火装置、中国的神光装置以及即将在欧洲建造的国际热核聚变实验堆装置等都是实现材料在极高温极高压状态的大型设备.在这些研究领域中所涉及的材料的物态方程其温度密度范围都非常宽广,从室温到几千万度,压强从常压到几千万大气压.在如此宽广的温度密度变化范围内,物质经历着固态、液态、气态、等离子体态等各种聚集态的变化,发生着相变、离解、电离等各种复杂的物理过程.在宽广的温度与密度范围内,如何准确给出材料的状态方程是一项富有挑战性的科学课题.

在高温高压下,物质全部熔化,出现部分离化或电离等复杂的物理变化过程.这种部分离化的强耦合电子离子系统给理论描述带来了很大的困难.托马斯-费米理论只适用于极高压强的物质状态(通常为几千万甚至亿万大气压).该模型不考虑原子的壳层结构,认为物质中的原子处于完全电离的状态.在千万大气压的压强段,物质中的原子实际上是处于部分离化的状态,即一部分电子仍然被束缚在原子核周围,另一部分电子则处于游离状态.也就是说,物质在高温高压“过渡区”的状态实际上是一种部分离化的等离子体状态.由于在这个区域内,粒子之间的相互作用很强,多体微扰理论不适用.而且,由于存在多种粒子的激发态,使得统计物理计算十分困难.

用于该区域的理论模型有物理图像法和化学图像法.物理图像法中的逸度展开方法[2]只能用于高温低密度系统.对于温稠密系统的物态方程,一般都采用化学图像方法计算.化学图像方法需要先给出系统的自由能,如俄罗斯科学家Fortov等[3]提出的自由能模型,以及美国和欧洲科学家Saumon,Chabrier,van Horn提出的自由能模型,即SCVH模型[4].液体微扰理论和粒子之间的相互作用势是该类模型的理论基础[5−7].在用SCVH模型对氢高压物态方程的研究中,他们发现了一种等离子体相变,即氢从导电率很低的绝缘态到导电率很高的金属态的转变.

除了上述物理与化学图像外,处理部分离化的等离子体系统还可以采用经验模型,如Kerley[8]提出的离化电离平衡模型.将该模型与液体微扰理论相结合,可以获得宽广的温度与密度范围内的物态方程[9].该模型是建立在经验内插基础之上,它有很多的经验参数,确定起来很困难.有些参数需要靠冲击波实验以及其他一些实验才能确定[10].

平均原子模型是将等离子体中的复杂离子系统等效为一个原子,用一个原子的性质来表达整个系统的性质. 最有代表性的就是Rozsnyai[11]的EOSTA模型和Liberman[12]的INFERNO模型.该模型在过渡区物态方程的计算中也取得了相当的成功.朱希睿和孟续军[13]对Rozsnyai的EOSTA模型进行了推广,并将其用于Au,Al,Hg等材料的电子热能热压计算.通过改进计算方法,INFERNO模型已经用于Al,Be,U等材料高压雨贡纽的计算[14,15].Barshalom和Oreg[16]通过修改维里定理的表达方式,得到了与实验符合得较好的冷能冷压.最近,马桂存等[17]又将该模型用于金高压雨贡纽的计算.上述平均原子模型的共同特点是考虑了束缚态电子的压致离化和温致离化效应,能够比较好地用于过渡区.但该模型也有很多不足之处,主要是没有考虑离子本身的热运动,以及没有考虑其他离子的热运动对所研究的平均原子内的电子态的关联影响.

在物态方程的数值模拟方面,目前主要采用量子分子动力学和量子蒙特卡罗方法.分子动力学(如VASP[18])只能用于较低的温度,一般认为其适用的温度不超过10 eV.尽管人们也提出了高温数值模拟方法,如无轨道分子动力学方法[19].但是,如何构造密度泛函和粒子之间的相互作用势仍然是没有解决的问题.量子蒙特卡罗方法虽然是用于多体相互作用系统比较好的数值模拟方法.但由于其计算量大,计算方法复杂,目前仅用于低原子序数材料的物态方程计算[20,21].

混合物的物态方程在实际应用中也非常重要,如人们在研究木星的构造时,就需要氢和氦混合物的物态方程.无论是用物理图像法,还是化学图像法计算混合物的物态方程,其计算量将成倍地增加.此外,如何给出不同种类粒子之间的相互作用势也是一个非常复杂的问题.目前的第一原理计算只能模拟上百个原子,所以在目前的计算条件下,完全用第一原理方法来给出混合物的物态方程也是不现实的.因此,寻找从单质物态方程构造混合物物态方程的经验方法,就成为构造混合物物态方程的主要方法.其中,体积相加模型就是一种获得混合物物态方程的有效方法[22].

本文从两方面来介绍温稠密物质物态方程的计算方法.在第2节中,主要介绍温稠密物质物态方程的理论模型,其中,包括考虑原子内部电子热激发效应的流体变分微扰理论、化学图像模型SCVH、离化电离平衡模型IEQ、平均原子模型和INFERNO模型以及混合物态方程的计算方法.在第3节中,主要介绍第一原理分子动力学方法和量子蒙特卡罗方法,以及这两种方法在氢、氘、氦、金、钨等材料物态方程计算中的应用结果.最后,给出本文的总结.

2 物态方程的理论模型

2.1 液体变分微扰理论

液体是常见的一种物质状态,是固体熔化或气体在低温下被压缩形成的一种状态,它的物态方程在物态方程的理论研究中占有十分重要的地位.由于液体分子在空间排列无序,以及粒子间存在很强的相互作用,理论上给出液体状态方程都采用变分微扰论方法.在给定粒子之间相互作用势的基础上,以硬球模型或软球模型为参考态来建立计算液体物态方程的理论计算方法,被称之为液体变分微扰论(FVT)[23].传统的液体物态方程理论模型是不考虑系统中粒子内部电子的激发.这种近似在低温下是可行的,但随着温度的升高,电子被激发到高量子态,甚至电离.在本节中我们将考虑这种热效应对物态方程的贡献,并称考虑热效应的液体变分微扰论为IFVT.

对于给定温度和密度的热力学系统,亥姆霍兹自由能是系统的热力学特征函数,完全决定系统的热力学性质.所以,模型的建立从构造系统的自由能开始.相互作用系统的自由能可以分为三个部分:

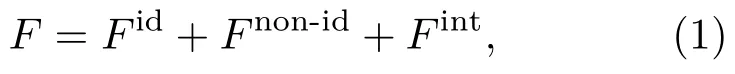
其中,Fid是理想气体部分,Fnon-id是相互作用引起的自由能,Fint是内部运动的自由能.根据液体变分微扰,系统的自由能为

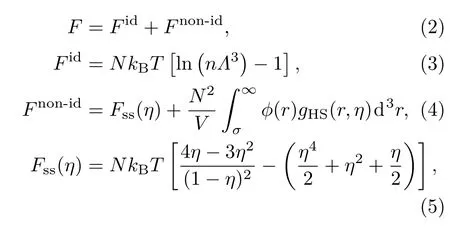
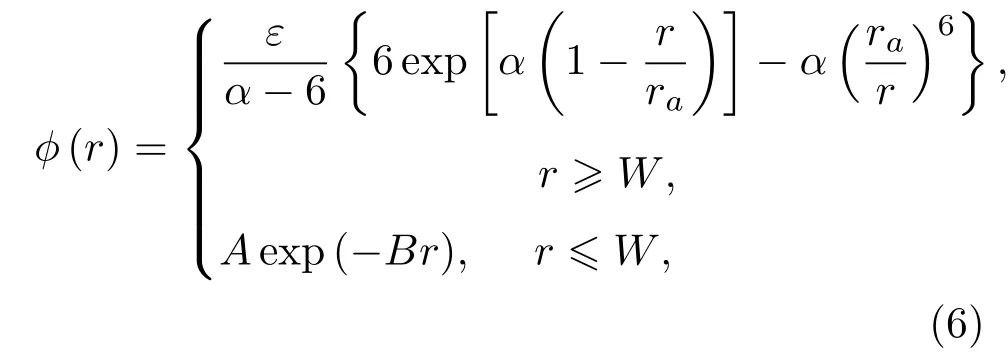
其中,参数ε=243.1 K,α=12.8,ra=4.42Å,W=1.28Å;近距离的非物理吸引势用指数衰减排斥势代替,A,B的取值保证函数值和一次导数在衔接处连续.对上述自由能变分,可求得与自由能极小值相对应的硬球直径.

考虑到热效应修正,自由能需要增加原子的壳层电子跃迁项Fint,

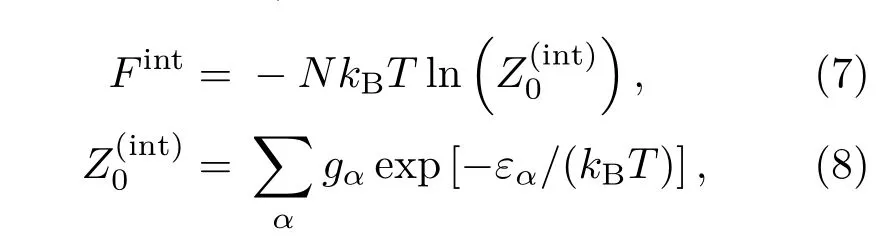
其中,gα和εα分别是氙原子第α个能级的简并度和能量,数值取自NIST数据库[24].

基于上述液体变分微扰方法,我们计算了氙的雨贡纽压强和温度,并考查了热效应修正的影响,其结果如图1和图2所示,其中FVT和IFVT分别为传统的液体变分微扰方法和考虑了热效应修正的液体变分微扰方法.从6 g/cm3处开始热效应修正显著降低了雨贡纽压强和温度,使其与实验数据[25,26]符合更好.这是由于壳层电子跃迁能够吸收冲击波能量,使得原子的热运动能量减少,从而显著降低温度和压强.由此可以看出,采用原子的壳层电子跃迁项能够比较准确地描述液体变分微扰方法的热效应修正,使得雨贡纽压强和温度的计算值在较大范围内得到显著改善,与传统的液体变分微扰方法相比,热效应修正使得模型的适用范围得到了较大扩展.

图1 氙的Hugoniot压强随密度的变化,冲击初态为165 K,2.96 g/cm3Fig.1.The Hugoniot of xenon,the initial state is 165 K,2.96 g/cm3.

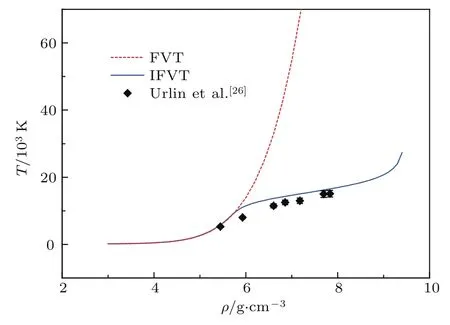
图2 氙的Hugoniot温度随密度的变化,冲击初态同图1Fig.2.The Hugoniot temperatu re changes with density,the initial state is the same as that in Fig.1.

2.2 化学平衡模型

当温度逐渐升高或密度进一步增大,就会引起分子的离解和原子的电离,形成分子、原子、离子和电子的混合物.对于这样一个复杂的系统,计算该系统物态方程的方法主要有自由能极小方法.Saumon,Chabrier和van Horn提出了一种计算系统自由能的方法,即SCVH模型[4−6].该模型是一种化学图像法,即事先假定系统中包含有哪几种物质成分,如分子、原子、离子以及电子等,然后根据系统的自由能极小来确定各种成分的比例.下面我们将以氢为例来具体介绍SCVH模型.

在低温下,氢以分子形式存在,当温度升高或密度增加时,会发生氢分子的离解和氢原子的电离.SCVH模型分两步给出了系统的自由能,首先给出氢分子和氢原子混合物的自由能,然后再给出氢离子(即质子)和电子组成的等离子体系统的自由能.对于氢分子和氢原子组成的混合物,它的自由能为

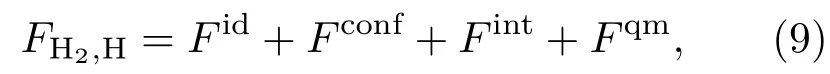
其中,Fid是分子或原子的质心运动动能;Fconf表示相互作用引起的自由能,即H2-H2,H-H以及H2-H之间相互作用导致的自由能;Fint是由分子内部自由度和原子内部自由度导致的自由能,即分子的振动与转动以及原子内电子热运动的能量;Fqm是考虑分子和原子自身运动的量子效应修正,它是一个小量,由W igner[27]和Kirkwood[28]的ħ2展开方法给出.对于相互作用部分Fconf,则采用以硬球系统为参考系的Weeks-Chand ler-Andersen形式的液体微扰论方法[29−31]计算.准确给出分子与分子、原子与原子以及分子与原子之间的相互作用势是本模型的关键.H2分子之间的有效两体相互作用势用冲击波实验数据拟合确定,H原子之间以及H2分子与H原子之间的相互作用势由第一原理方法给出.由于SCVH模型涉及压致离化区域,所以Fint部分采用Hummer和Mihalas[32]提出的占据概率方法计算,

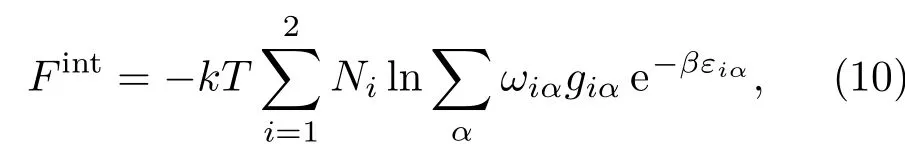
式中,下标i=1,2分别对应于H2,H;ωiα表示束缚态α存在的概率(0≤ ωiα≤ 1);Ni表示系统中分子或原子的数目;εiα,giα分别表示分子或原子内部运动的能级和简并度.

对于由质子和电子组成的等离子体系统,SCVH模型采用屏蔽的一元等离子体模型描述,即认为质子在由电子组成的负电荷背景中运动,离子之间的相互作用势用屏蔽的库仑势Veff描述.这种模型被称之为SCOP(screened one component plasma),它的自由能为[6]

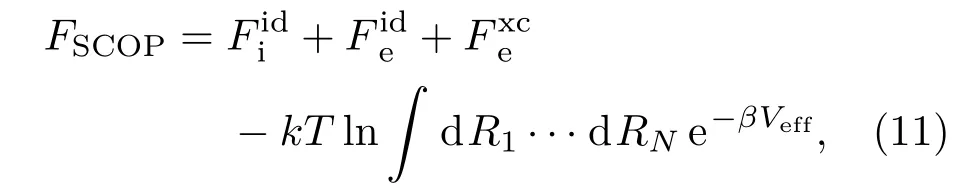
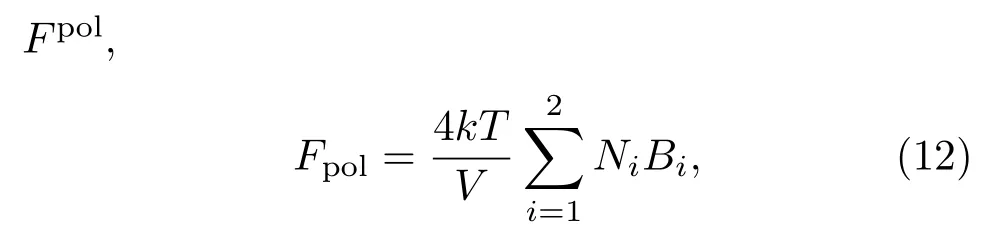
所以,整个系统的自由能为

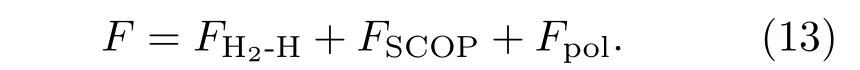
在给定的温度和密度下,通过求系统的自由能极小,可以给出各种粒子成分的含量.此外,通过热力学关系式,可以求出系统的内能、压强等物理量.图3给出了氢原子的浓度随温度密度的变化关系[5].温度从2884—18197 K在对数坐标下等间隔分布.从图3可以看出,在低温(T＜3000 K)下,氢分子含量比较多,氢原子占的比例比较少.随着温度的升高,氢原子的浓度在低密度区由小变大逐渐接近于1,这表明温致离解效应在该区域起作用.其次,随着密度的增加氢原子浓度在减小,在密度为0.5—1.0 g/cm3内有一个明显的转变,它反映的是压强导致的离解和离化效应.即在给定的温度下,当密度大于1.0以后,系统中的氢分子将不复存在,取而代之的是氢原子或氢离子.图4给出了氢的物态方程,即压强随温度密度的变化[4].其中的两条低温等温线出现了明显的转折,它反映了在该区域出现了等离子体相变(plasma phase transition,PPT),即从导电率很低的绝缘体状态转变到导电率很高的金属状态.该相变类似于气液相变,即物理量存在不连续变化,且有临界点存在.这种相变的内在机理就是压致离化,即由压强或密度的增加而导致的凝聚体物性的突变.关于PPT的详细讨论请看参考文献[6].

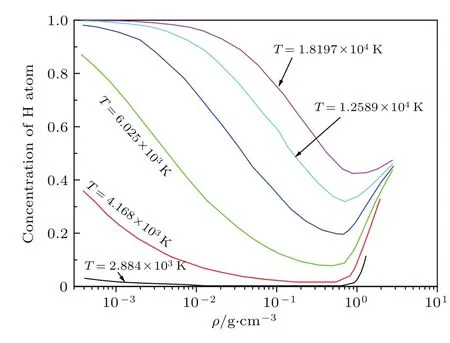
图3 在一系列的温度下氢原子的浓度随密度的变化Fig.3.The concentration of Hatomchanges with density at a series of temperatu res.

图4 氢在一系列温度下的等温线Fig.4.The equation of state of hyd rogen at a series of temperatu res.

2.3 离化电离平衡模型

上节中的SCVH模型依赖于粒子之间的详细相互作用,给出粒子之间的相互作用势是一项复杂而繁重的工作.在本节中,我们将在经验模型的基础上,给出氘的物态方程.在给定的温度和密度下,对于由单一成分组成的系统,其能量和压强通常写成如下三项式形式:

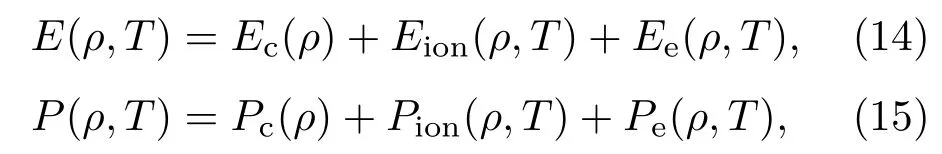
其中,Ec,Pc为冷能、冷压;Eion,Pion为离子的热能、热压;Ee,Pe为电子的热能、热压.对于由氘分子,或氘原子组成的系统,其冷能、冷压都用如下经验公式描述[9]：

式中,EB是结合能;δ= ρ/ρ0;α,ν是可调参数,可根据实验数据给出.

离子部分的贡献由修正的硬球模型(即CRIS模型[34−36])给出:

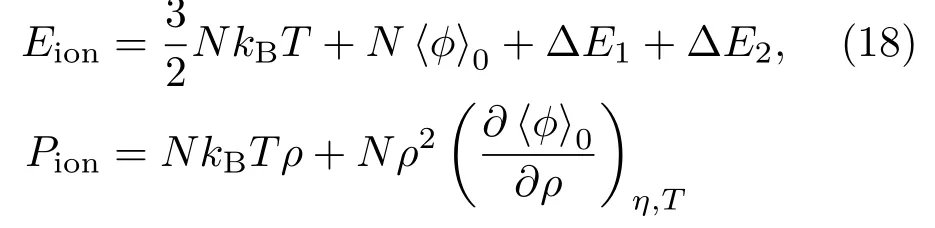
式中N〈ϕ〉0是一级势能项[34];为硬球系统的堆积因子(packing fraction of hard sphere);∆E1,∆E2,∆P1,∆P2是高价修正项[35,36].

热激发的电子对物态方程的贡献采用离化电离平衡模型(IEQ)计算[8].设在体积为V和温度为T的系统中,含有N个粒子,它包括不带电的中性原子和带正电的离子.原子的核电荷数为Z,原子量为W.每个原子或离子的电子结构是通过指定每个轨道上的电子占据数来确定,然后,根据量子力学原理来确定每个电子的轨道能量,系统的宏观量是各种离子成分贡献的统计平均.在描述电子运动时,要区分电子的两种状态,一种是束缚态,一种是巡游态.处于束缚态的电子只能围绕原子核运动,一般用原子轨道波函数描述;处于巡游态的电子可以在整个系统中运动,一般用平面波描述.该模型的优点是它考虑了各种离子成分对物态方程的贡献.系统的自由能可以表示为[8]

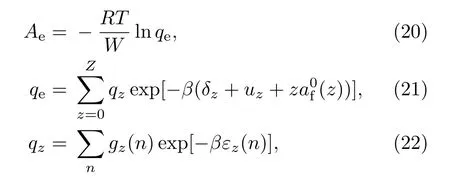
其中,qe为系统的配分函数,qz为带电荷为z的离子的配分函数.(21)式中的求和是对各种离子态进行的,各种离子态的电荷数分别为z=0,1,2,3,...,Z,共包含Z+1种离子态;uz为带电荷z的离子的基态能量;a(z)为一个自由电子的自由能,电中性要求每个离子平均含有z个自由电子;δz表示每个原子的电荷涨落.(22)式中的求和表示对每个离子的能级进行求和,其中εz(n),gz(n)分别表示离子的各个量子态的能量和相应的简并度.为了能够使上述模型准确地描述电子的电离态,必须做一些修正,如连续谱能量修正、电荷涨落效应和体积涨落效应修正等.

根据上述物态方程理论模型,我们计算了液氘在一定的温度与密度范围内的物态方程,并计算了液氘在一定的压力范围内的雨贡纽.图5和图6给出了液氘的低压和高压雨贡纽,同时也给出了雨贡纽实验点、第一原理计算以及各种理论模型的结果.

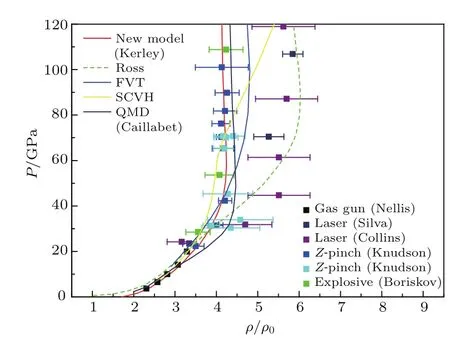
图5 液氘的雨贡纽(低压部分)Fig.5.The Hugoniot of liquid deuterium(lowpressure part).

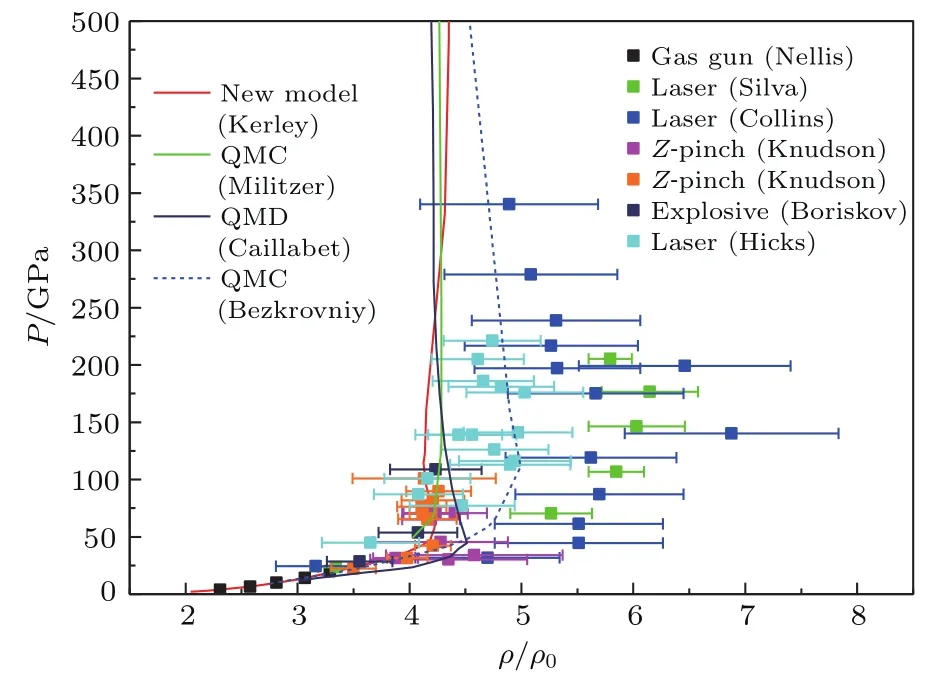
图6 液氘的雨贡纽(高压部分)Fig.6.The Hugoniot of liquid deuterium(high pressu re part).

目前用于测量液氘雨贡纽的实验有四类:第一类是化爆和二级轻气炮[37],它们给出的雨贡纽压强只有20 GPa(见图中Gas gun);第二类是球面内爆[38],它的压强达到110 GPa(见图中Explosive)；第三类是Z-pinch[39],它达到的压强也有100 GPa;第四类是强激光实验[40−42],它达到的压强有350 GPa(见图中Laser).较早期的强激光实验[40,41](见图中Silva和Collins)由于其测量的方法导致的误差非常大.所以,它给出的雨贡纽线最大压缩比也非常大.后期的Z-pinch、球面内爆以及强激光实验结果[42]都给出了较小的最大压缩比.最早的第一原理计算结果是由美国科学家Militzer和Ceperley[43]用量子蒙特卡罗方法在2000年给出(见图中QMC).后来的第一原理计算结果,如采用直接积分的量子蒙特卡罗方法[44]以及第一原理分子动力学计算结果[45](见图中QMD)都表明,液氘雨贡纽的最大压缩比为4.65左右.同时,在这一时期,物态方程的理论模型也得到了很大的改进.Ross[46]的线性混合模型提出得比较早,该模型给出的雨贡纽曲线的压缩比也比较大,与早期的激光实验结果差不多.后来提出的物态方程理论模型,如液体变分微扰理论[7,23](见图中FVT),Saumon和Chabrier[4−6]的化学平衡模型(见图中SCVH),以及在本节中以Kerley的Sesame物态方程模型为基础新做的物态方程(见图中Newmodel[9]),都给出了较小的压缩比.

2.4 INFERNO模型

INFERNO模型是在固体凝胶模型中加入一个原子而形成的平均原子模型.在通常的固体结构中,带正电的离子按照一定的方式排列,在每个离子周围又有很多电子,它们代表核芯电子与价电子(或巡游电子).核芯电子只能在束缚它的原子核周围运动,而巡游电子属于整个系统,可以在物质内部自由运动.在量子统计自洽场INFERNO模型中,认为正离子是均匀分布在整个空间的,同时,为了保持系统的电中性,也有均匀分布的同样多的负电荷存在,这种模型被称为凝胶模型.现在,在凝胶模型中加入一个原子,该原子的核电荷位于系统中央,为了保持系统的电中性,在以原子核为中心,原子半径为大小的空间内,所有的正电荷将被排斥掉,剩下的是按照量子力学规律分布的负电荷.这种模型通常被称之为INFERNO模型[12,47].

在INFERNO模型中,球内电子的波函数满足相对论形式的单电子狄拉克方程[12,47]:

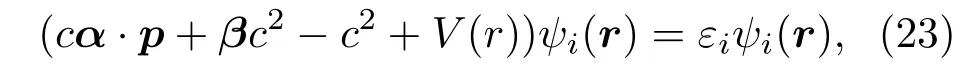
式中α,β是Dirac矩阵,c是光速.在原子球内(或muffi n-tin球内)的势函数V(r)可以表示为

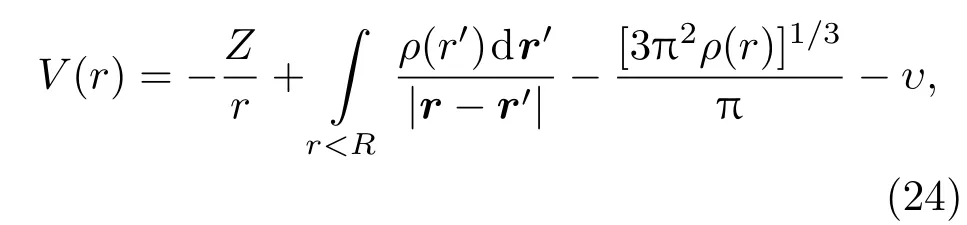
其中,Z是核电荷数,ρ(r)是球内电子电荷密度分布,R是原子球半径,υ为拉格朗日乘子.mu ffi n-tin球外的势函数可以表示为

在INFERNO模型中,电子的状态被分为束缚态、共振态、巡游态(或散射态)三种类型,电子的波函数要通过自洽求解量子力学的Dirac方程获得.电子所受到的势场是一个自洽的多体势,它包含了电荷之间的库仑能,以及多体效应引起的交换关联能.共振态、散射态的出现给理论计算带来了很大的困难[47],特别是在高能量、高角动量的情况下,电子波函数要发生剧烈振荡,这些问题的出现使理论计算非常复杂.为了克服上述困难,美国利弗莫尔实验室的科学家提出了用位相-振幅形式的波函数方法[14]来描述电子态,克服了高能量的连续谱在计算上困难,得到了很好的结果.2009年,法国原子能科学研究中心的科学家提出了采用大规模并行计算的方法[15]来克服高能量积分,高角动量求和困难.2011年,俄罗斯科学家也用类似的方法计算了INFERNO模型的物理量[48].除了在计算方法上得到改进外,最近,以色列科学家又对INFERNO模型在压强计算上进行了改进[16,49,50],提出了根据维里定理计算压强的方法,得到了与实验一致的很好结果.

我们利用INFERNO模型,对Au在宽广的温度与密度范围内的物态方程进行了计算[17].图7给出了金属Au中的电子压强随密度的变化,每一条线对应一个温度.温度从log10(2.3×103)到log10(4.8×106),等间距分布.从图7可以看出,在比较低的温度下,电子系统的压强随密度都发生了非单调变化.引起这个变化的主要原因是Au原子中的外壳层电子的状态发生了变化,即从束缚态变成了巡游态,这种转变被称之为绝缘体金属转变或Mott转变[51].对发生这种转变的理解并不是非常困难.设想初始时,系统中的Au原子处于密度小于10 g/cm3的某个状态,显然,在这种状态下,Au的外壳层电子被原子核束缚,整个系统是绝缘体.如果在温度不变的条件下,对系统进行压缩,在某个密度下,Au原子的外壳层电子波函数就要发生重叠,它将引起外壳层的d电子和s电子从束缚态变成巡游态.转变完成,整个系统将变成金属.这一转变的主要特征是其d电子能谱由宽变窄,再变宽,即d电子由束缚态变为共振态,再变为巡游态.这种现象被称之为压致电离效应[47,51],即由压强引起的电子态的转变.在用INFERNO模型对Au全区域物态方程的计算过程中,在某些温度密度点处经常会遇到共振能态,它是由压强或温度变化引起的电子状态的变化.共振能态的主要特点是其态密度有尖锐峰出现,而且峰宽非常窄,这给计算带来了很大的困难.为了克服这一困难,我们对共振能态的特点进行了仔细的分析,得到了计算连续谱的波函数的有效方法[47],这种方法对处理共振能态特别有效.

对于离子热运动部分,我们采用一种内插模型来描述固态或液态系统的物态方程,它就是大家常用的自由体积模型[1].在给出了物态方程的各个部分贡献之后,就可以按照三项式形式的物态方程计算材料的雨贡纽.图8给出了Au的理论雨贡纽.为了比较,我们也在图8中给出了利用一些加载设备如化爆、二级轻气炮等从实验上获得的金材料的高压雨贡纽[52−55].从图8可以看出理论与实验符合得非常好.在很高的压强下材料的雨贡纽曲线发生了弯曲,它是由原子的内壳层电子的离化从而吸收冲击波能量所致.

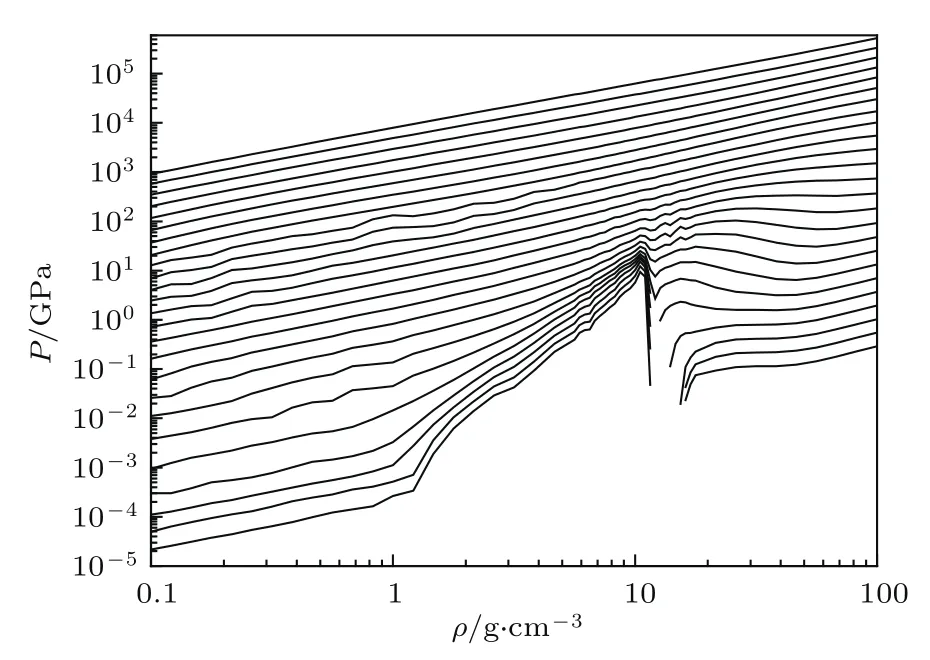
图7 在一系列温度下Au中的电子热压随密度的变化Fig.7.The electronic pressure of gold changes with density at a series of temperatures.

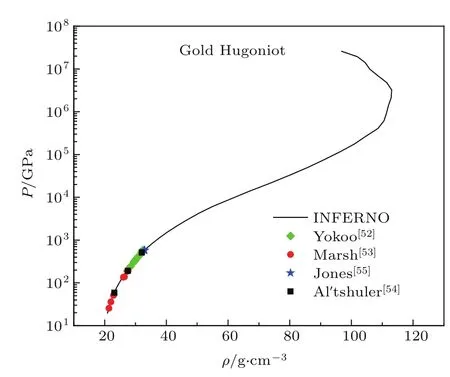
图8 Au的高压雨贡纽曲线,其中,实线是理论结果Fig.8.The Hugoniot curve of gold at high pressu re,solid line is the resu lt of theory.

2.5 平均原子模型

在前面几节,我们已经涉及了物质中的原子的离化或电离效应,如在SCVH模型、INFERNO模型以及IEQ模型中,都考虑到了原子的电离效应.在每一种模型中,都给出了用一定的方法来处理周围的带电粒子对所考虑的离子的影响.INFERNO模型对束缚电子与自由电子之间的转换做了自洽处理.实际上,在部分离化的等离子体区域,还有另一种经常使用的平均原子模型,即Rozsnyai[11]给出的平均原子模型.它是基于温稠密物质的等效原子模型思想,即认为在整个系统中每个原子都是等价的.这样每原子周围的环境都是一样的,因而导致在原子边界上的电荷密度是连续的,周期性边界条件要求电荷密度的导数也应连续.这些条件界定了离子内部束缚电子的占住方式.自由电子和准自由电子的存在,以及离子内部电子细致组态的考虑,使模型在计算上变得比较复杂.在Hartree-Fock理论的框架下,电子的运动方程为

其中 Vsc(r)为自洽势,ϕi(r)为单电子波函数,εi为单电子能级.在球坐标系下分离变量,可得到径向波函数Pnl(r)满足的方程.考虑到电荷密度及其导数的连续性,径向波函数Pnl(r)应满足下列两种形式的边界条件：

第一种边界条件取为

周期场中的电子,其波函数一般要受到简谐波的调制.对应来讲,波函数按第一类边界条件衔接时是因为整个物质内部处于最低能态,按第二类边界条件衔接意味着物质内部已处于最高能态.由于物质内部调制波的周期是最基本周期的整数倍,那么原子间波函数的连接就不只是第一类和第二类边界条件,还可能是中间过渡的边界条件.

严格确定原子的波函数取第一类边界条件还是第二类边界条件是没有太大意义的.当原子中的电子波函数取第一类边界条件与第二类边界条件之间的允许值时,电子的能级就具有了一定的范围,这个能级范围也可以叫做“能带”.不过这个能带的起源与固体理论中能带的起源本质是不同的.这个“能带”对确定有界原子束缚态波函数的能态密度具有重要意义.能带的出现使得高温稠密等离子体的原子结构求解更加复杂.为了简化模型,一般取第一类边界条件.

原子胞中的电子被分为束缚电子和自由电子,其数密度可以写为

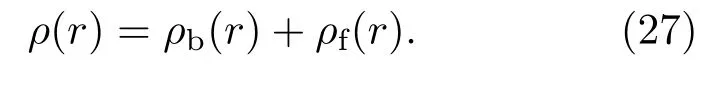
自由电子的数密度ρf(r)本应由自由电子的正能态波函数来确定,但由于正能态能量、轨道量子数都是无限的,为了快速计算,采用分波加统计的方法解决,并且具有较高的精度.自由电子数密度ρf(r)可以写为

其中,V(r)是自洽势,µ是化学势,T是温度,l0是分波的界限,其取值视所需计算量和精度所定.束缚态电子的数密度ρb(r)为

关于压强的计算,由于已经把一部分波函数能延伸到原子边界处的束缚电子划归准自由电子用分波法处理,所以剩下的束缚电子的径向波函数就基本不能延伸到原子边界处,这样电子压强就只能与非束缚电子有关.这样我们得到的电子压强就可以只由三部分组成:

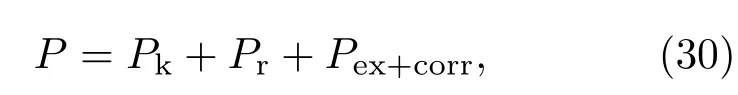
其中,Pk为自由电子产生的动压,Pr为分波电子产生的压强,Pex+corr为交换、关联效应综合产生的负压.

在含温有界原子模型下,精确的原子总能量由四部分组成:束缚电子的组态平均能量Ebav,自由电子的单电子能Ef、束缚电子与自由电子间的相互作用能Eb-f,自由电子与自由电子间的相互作用能E f-f,即

关于压强和能量的各部分贡献的详细计算请看参考文献[13,56].由于我们的含温有界模型是自动包含温度、密度效应的,并且由于部分分波法的引入大大降低了高温下原子参数和状态方程参量的计算量,因而我们可以在保证相当的精度下快速得到任意温度密度下的状态方程参数.

图9和图10展示了本模型计算的Au在温度分别为0.1,5.0,10.0,50,100,500,1000 eV下,电子压强P和原子能量E随物质密度的大范围变化(密度为1.0—5000 g/cm3,基态能E0=−17865.2288 a.u.).从计算结果中可以看出,在密度为20 g/cm3以及70 g/cm3处均显示出了较强的原子壳层效应,这是由于原子壳层的压制离化所导致的.在图10中,原子的能量不再随密度的增加而稳步上升,甚至会出现随密度的增加原子能量降低的现象.这是由于本模型考虑的是孤立原子的能量,在密度比较稀时,低壳层会出现一些空轨道,而密度的增加标志着压力的增大,会把一些外壳层的电子压回低壳层的空轨道上,使得电子的总势能下降,从而造成整个原子的能量会有所降低.

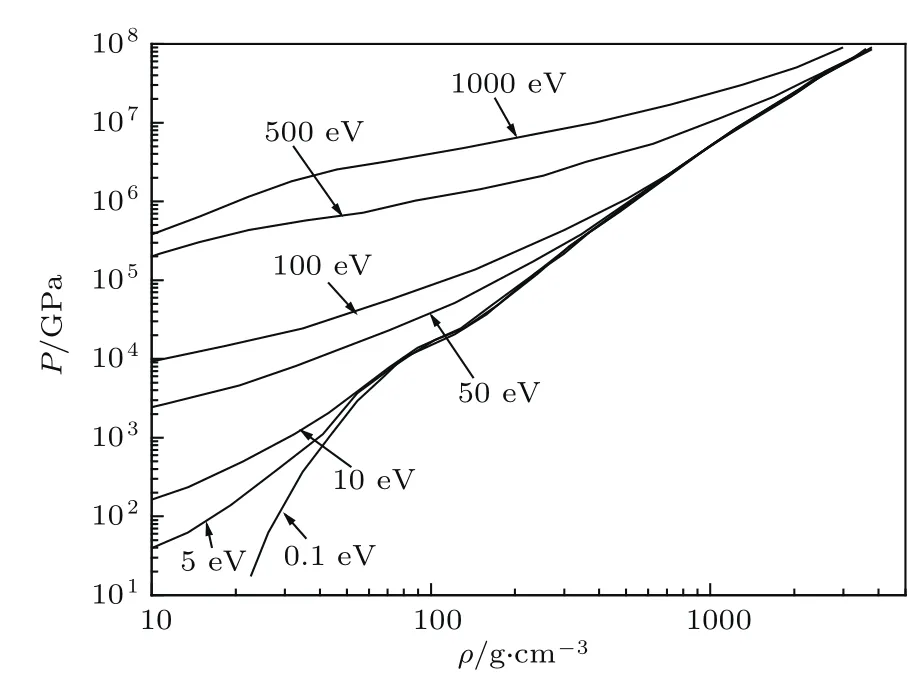
图9 在一系列的温度下Au电子压强随密度的变化Fig.9.The electronic pressu re of gold changes with density at a series of temperatu res.

图10 在一系列的温度下Au原子能量随密度的变化Fig.10.The energy per atomof gold changes with density at a series of temperatu res.

2.6 混合物物态方程

在激光惯性约束聚变以及天体物理的行星构造研究中,人们经常会遇到混合物情况.如何给出混合物物态方程是备受关注的一个问题.例如在研究木星构造时,就要知道氢与氦混合物的状态方程.木星表层中[57]氢占74.2%,氦占23.1%,其他元素占0.027%.前面几节介绍的物态方程计算方法都是对单一成分而言的,对于由多种元素组成的混合物,如果按照液体微扰论方法计算物态方程,那就需要给出不同粒子之间的相互作用势,这在实际问题中很难做到.如果按照第一原理计算方法求物态方程,对于不同的混合比都一一去做数值计算,其计算量也是相当大的.所以,有必要寻找一种从单质物态方程计算混合物物态方程的经验方法.线性混合模型或体积相加模型可以比较好地给出混合物的物态方程.在这个模型中,认为在等温等压条件下,混合物的体积是单质成分在与混合物有相同的压强和温度下的体积之和,即

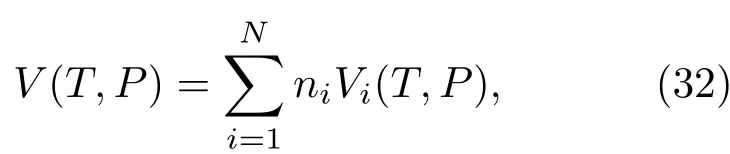
其中,N是混合物中组元的总数,ni是第i组元的摩尔分数.如果用质量百分比χi来表示,即

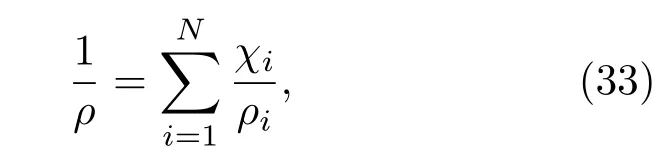
其中,ρ是混合物的密度,ρi是组元i的密度.系统的内能为

系统的熵为

其中,Ei,Si分别是组元i的内能和熵;Smix是混合熵增.

下面以氢与氦混合物为例,具体讨论体积相加模型在物态方程计算中的应用.图11给出了用体积相加模型计算的氢氦混合物的物态方程,氢与氦的原子个数比为NH:NHe=2,同时我们将第一原理分子动力学(QMD)计算结果[22]也标注在图中,可以看出两者符合得比较好,说明体积相加模型是计算混合物物态方程的一个很好的近似计算方法.但是,用第一性原理分子动力学和量子蒙特卡罗方法对氢氦混合物物态方程的详细研究表明:在某些温度密度范围内,线性混合模型与第一原理结果相比却给出了高达12%误差[22].我们也用分子动力学方法计算了氘氦混合物的物态方程[58].定义混合比x=NHe/(NH+NHe).图12给出了氘氦混合物在压强P=10 GPa,不同温度、不同混合比下的体积差:∆Vmix/V=(VLM−V)/V随混合比x的变化,其中V是实际体积,VLM是混合模型给出的体积.从图12可以看出,在高温下,混合比x接近0.5时,偏差最大,最高可达到8%.研究表明,氦混合到氢中会对氢分子的离解产生一定的影响.同时它也对氢原子的电离产生一定的影响.这种影响在某些情况下是无法用线性混合模型来表达的.

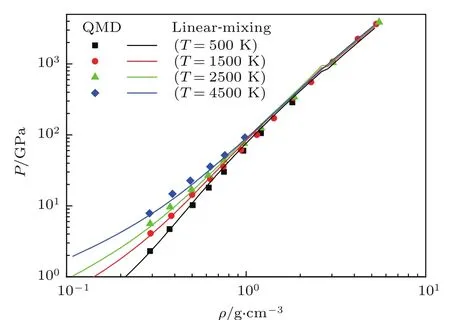
图11 在不同温度下氢氦混合物的物态方程,其中,实线是体积相加模型的结果,数据点是第一原理分子动力学结果[22]Fig.11.The equation of state for Hand He mixing at d iff erent temperatu res.lines are the resu lts of add itive volume,dots fromQMD[22].

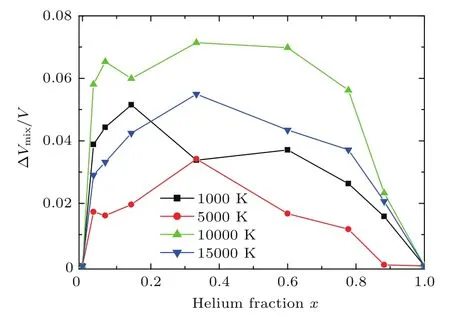
图12 在压强为10 GPa时不同温度下体积差随混合比的变化Fig.12.The volume d iff erence changes with mixing fraction of Heliumat pressu re 10 GPa.

如果我们定义系统的过剩压强为总压强与理想气体压强之差,即Pex=P−Pid,则在线性混合的假设下,让每个单一成分按照等温等Pex混合,其混合体积仍然是各成分的体积之和,那么按照这种方式得到的混合物物态方程与第一原理的差别会更小[59].从热力学上看,这种让过剩压强相等的混合模型相当于认为混合系统是由独立的平均有效原子组成,各种有效原子之间不存在相互作用,混合系统的过剩自由能就是每个有效原子的自由能之和.

3 物态方程的第一原理计算

在温稠密物质系统内部,粒子之间的关联相互作用非常强,随着温度和密度的变化在温稠密物质内部会发生部分离化、强关联以及量子效应等一系列复杂过程,特别是在金属绝缘体转变区域,很难找到一种有效的理论方法来描述其变化行为.第一原理分子动力学和量子蒙特卡罗方法为我们提供了认识该区域物态变化行为的有效数值模拟工具,两者都是解决多体问题的有效方法.第一原理分子动力学是建立在密度泛函理论基础上的有限温度数值模拟方法,量子蒙特卡罗方法是建立在路径积分基础上的一种随机行走方法.

3.1 第一原理分子动力学方法

计算材料在有限温度下状态方程的数值方法,目前比较常用的是基于密度泛函理论的分子动力学方法,通常称为量子分子动力学(QMD)方法[18,60],该方法通过Born-Oppenhaimer近似,将电子离子问题部分解耦合,每个离子都在电子与其他离子形成的有效势场中运动,离子受到的力通过Hellman-Feynman定理给出,离子运动按照经典力学规律描述.在离子运动的每个时刻中,电子运动由求解该时刻离子位置构型下的电子Hamiltonian系统来确定.QMD方法严重依赖赝势和交换关联势的准确性,同时随着温度升高,需要计算的能带数目增加,导致计算量大大增加,因此QMD不适合在很高温度下的材料模拟.在本节中,我们将介绍利用QMD方法对氦、金、钨的物态方程以及钨的电学性质的计算.

在分子动力学模拟中,一般采用超原胞和周期性边界条件,模拟的原子数越多,所需的计算量就越大,通常用64或128个原子就可以达到理想的结果.电子和离子之间的相互作用势选用超软赝势或投影缀加波赝势,交换关联泛函选用广义梯度近似Perdew-Burke-Ernzerhof[61,62]形式,倒空间布里渊区积分采用Monkhorst-Pack[63]方法或用单Gamma点方法;平面波展开的波函数截断能量一般为几百eV.平面波截断能量和k点的数目在实际计算时都要经过优化,以达到满足实际精度的要求.离子系统的运动釆用NVT系综描述,由Nose-Hoover[64]恒温器来控制离子温度,电子温度分布则根据Fermi-Dirac统计得到.

3.1.1 氦的物态方程

我们用分子动力学VASP程序计算了氦在10000 K和30000 K的等温线(见文献[58]图1).计算表明,在温度不超过30000 K,密度不超过5 g/cm3的范围内,用化学模型来计算状态方程是合理的.在更高的温度密度区域,则需要进一步改进模型.图13显示了根据物态方程计算得到的氦的一次冲击和二次冲击Hugoniot曲线,同时还显示了Nellis等[65]的实验数据.从图13可以看出,QMD和化学平衡模型(CM)的计算结果符合得很好,且一次冲击Hugoniot与实验数据一致,二次冲击Hugoniot结果与实验数据相比稍微偏软,这与实验点的精度有关.尽管如此,理论仍然在实验的误差范围.

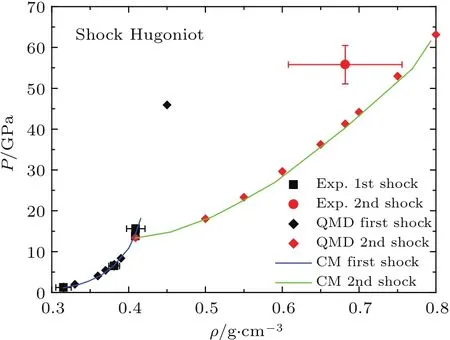
图13 氦的一次和二次冲击Hugoniot曲线Fig.13.The Hugoniot of heliumfromfi rst and second shock.

3.1.2 金的物态方程

我们用分子动力学方法计算了Au密度在19.3—42 g/cm3,温度在1000—50000 K区间的物态方程,并在此基础上得到了Hugoniot曲线[66],如图14所示[52,67−70].图中D是冲击波速度,u是粒子速度,其中的数据点是实验结果,粉色的曲线是马桂存等[67]在2005年用QEOS方法计算的结果.在低压区(u＜1.5 km/s),我们的结果与QEOS基本一致,且与早期的实验结果符合得很好.在1.5 km/s＜u＜6 km/s区间,我们的结果与QEOS方法计算的结果差别较大,Yokoo研究组[52]的实验结果与我们的计算结果更接近,QEOS方法计算的结果偏软,其原因是QEOS方法在做参数拟合时只用到了早期的化爆和气炮实验结果.在更高压区,目前的实验手段只有激光加载才能达到,但由于实验中各种复杂的因素导致激光加载实验数据的精度较差、数据点分散,因此实验结果不能用来标定理论数据.由此可以得出结论:仅利用低压的实验数据拟合参数得到的QEOS理论状态方程,不能保证在高压时的准确性;为了能使其用于惯性约束聚变数值模拟中,需要更多的高精度的高压实验数据来标定理论物态方程的参数.

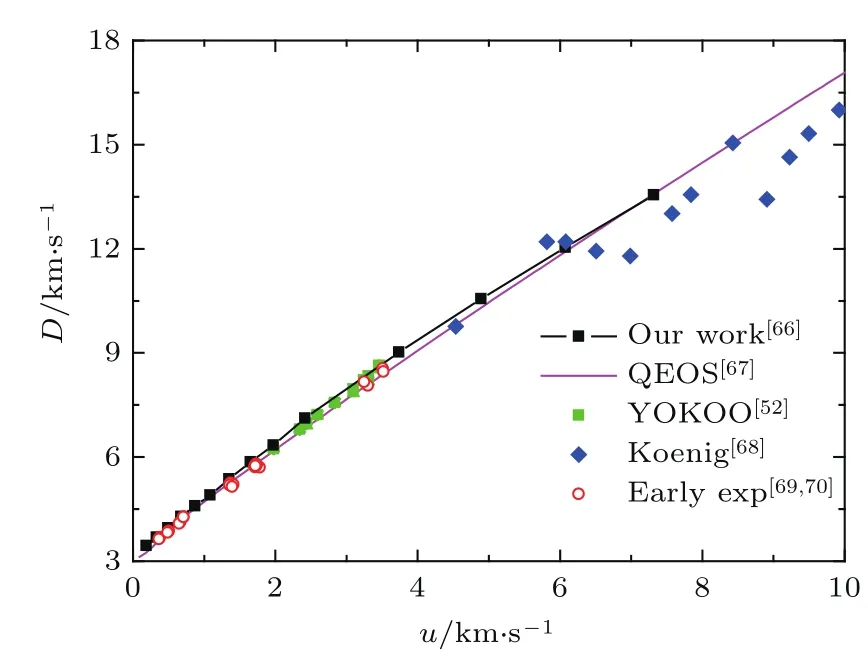
图14 金的冲击波速度与粒子速度关系Fig.14.The shock velocity changes with particle’s velocity for gold.

3.1.3 钨的物态方程

从理论上说,数值模拟膨胀态金属流体系统的金属-非金属转变非常困难,由于系统在极端条件下的无序性和热激发行为,体系成分复杂,包括离子、自由电子、中性原子、分子及团簇等,且各成分高度瞬时变化;此外物理过程也非常复杂,包括各种分解、激发、电离及其逆过程,体系成分及其中发生的物理过程强烈地受周围环境的影响,必须考虑多体效应以及关联相互作用.基于有限温度密度泛函理论的量子分子动力学方法提供了有效模拟极端情况下流体特性的工具.该方法对离子实采用经典分子动力学描述,对电子采用有限温度量子处理,并结合线性响应理论的Kubo-Greenwood公式,在统一的框架下计算材料的物态方程、光学性质、电学性质和热力学性质.

我们采用第一原理分子动力学方法研究了膨胀钨在较宽的温度与密度范围的物态方程,并与已有的实验结果进行了比较,如图15所示.以温度为300 K时的体积V0作为参考体积.其中,用QMD计算的等温线的温度分别为0,300,500,1000,1500 K.在图15中,我们还给出了Konstantin等[71]采用WC压砧,MgO-Au作为压标,给出的一系列温度下的压强实验数据.理论与实验符合得很好.

图15 金属钨在膨胀区的物态方程Fig.15.The equation of state for tungsten in the expanded region.

3.1.4 钨的电导率

我们利用分子动力学VASP程序计算体系的电导率,主要通过Kubo-Greenwood公式[72,73]计算电导的实部随频率的变化:

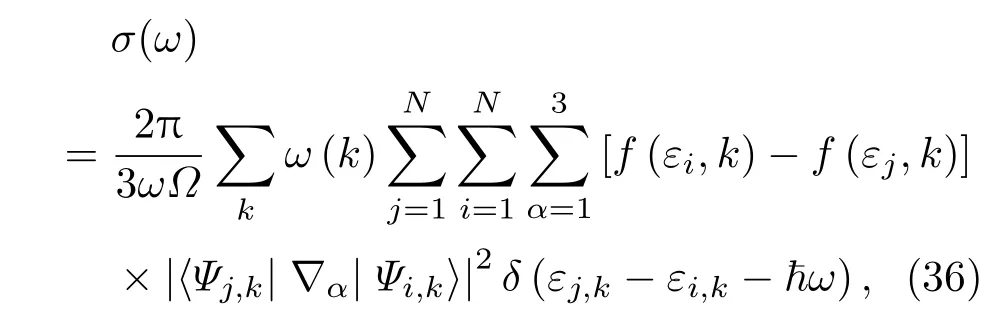
式中Ψi,k和Ψj,k为Kohn-Sham方程本征态,εi,k和εj,k为对应的本征值;f(εi,k)是电子占据数;ω(k)是k点权重.

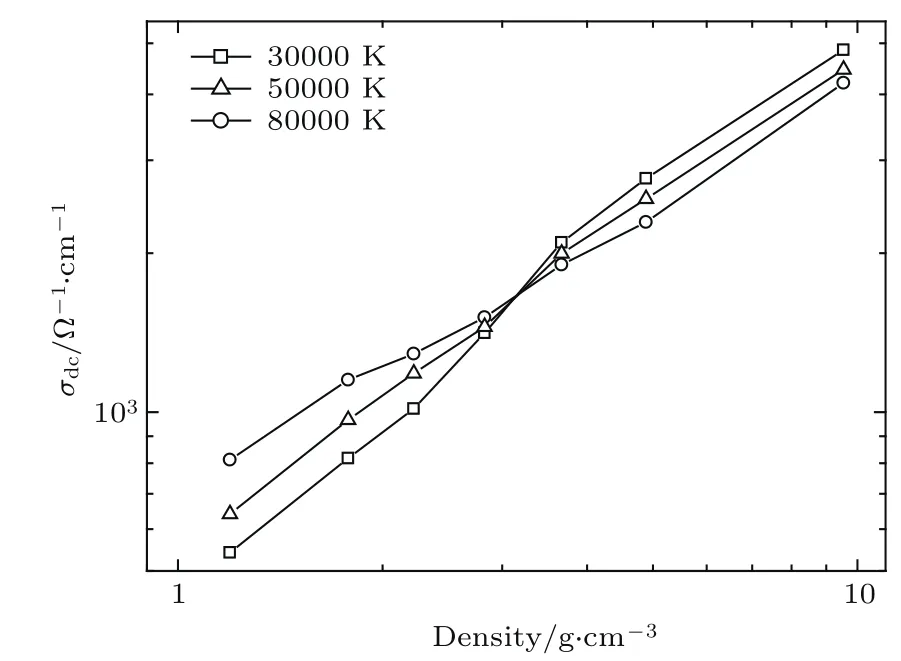
图16 在不同的温度下钨的静态电导率随密度变化行为,其中,在密度为3 g/cm3附近,电导率出现了反转,表明出现金属-非金属转变Fig.16. The static conductivity of W changes with density at d iff erent temperatures. Near density 3 g/cm3,the behavior of conductivity changed abruptly,which means that metal tonon-metal transition occu rred.

金属与非金属区别在于在电子能谱中是否有能带间隙,而带隙的出现可以通过电导反映出来.由于离化引起热激发,体系直流电导将随温度的增加而增大,但是随着密度的减小又将导致电导率的降低.体系的实际电导随温度和体积的变化关系是上述两种行为的竞争结果,体系发生金属-非金属转变需要低电子浓度以及达到一定程度的无序性,最终导致电子的局域化并引起金属-非金属相变.

3.2 量子蒙特卡罗方法

路径积分蒙特卡罗(PIMC)方法是比较适合的模拟系统有限温度性质的第一性原理方法[76].该方法已经很好地用于描述Bose系统的热力学性质,但对于Fermi系统,由于波函数的交换反对称性导致所谓的“负符号”问题限制了它的应用.为了解决这个问题,Ceperley等提出了约束路径积分蒙特卡罗(RPIMC)方法[76−78],Hu等[21]利用RPIMC方法计算了一套氘的状态方程数据.Filinov等[79−81]认为RPIMC方法引入了不可控的近似,他们发展了直接费米路径积分蒙特卡罗(DPIMC)方法,并成功计算了非理想氢等离子体平衡态的热力学性质.我们采用DPIMC方法对氢的状态方程进行了计算,并与QMD和RPIMC的结果进行了比较.

3.2.1 DPIMC方法简介

众所周知,量子系统的热力学性质完全由其配分函数Z决定.对于由Ne个电子和Np个质子组成的二元混合系统,其配分函数Z可表示为

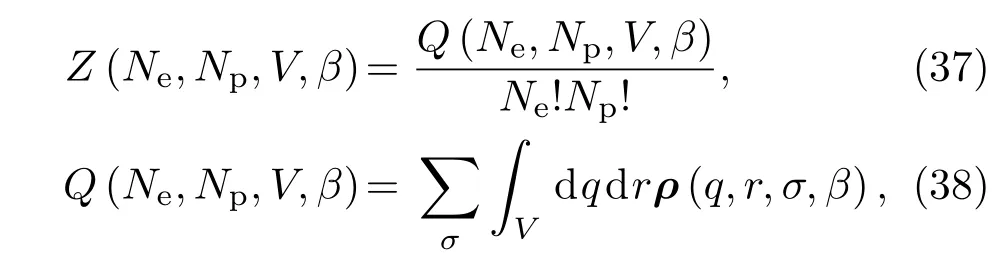
其中,β=1/kBT;q=q1,q2,...,qNp和r={r1,r2,...,rNe}分别表示质子和电子的坐标;σ={σ1,σ2,...,σNe}表示电子的自旋态.ρ是密度矩阵,可以表示为路径积分的标准形式:

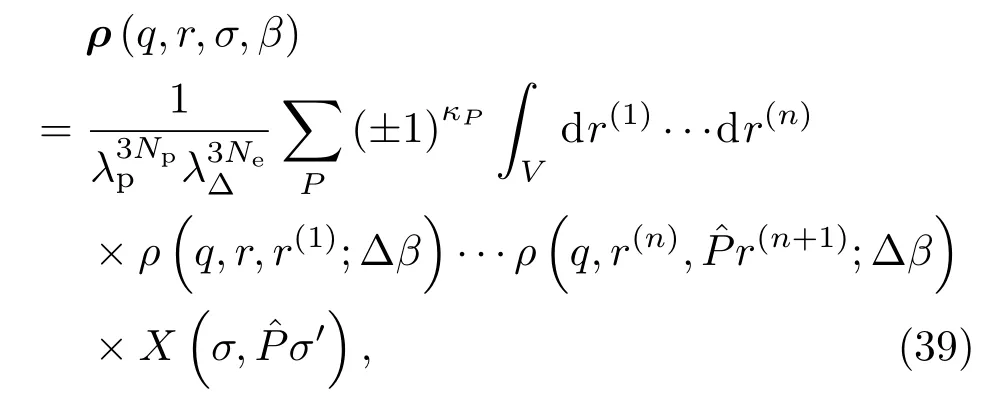
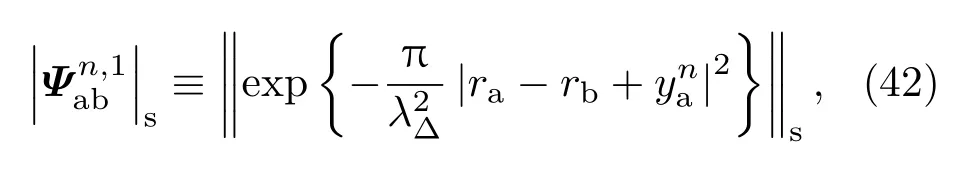
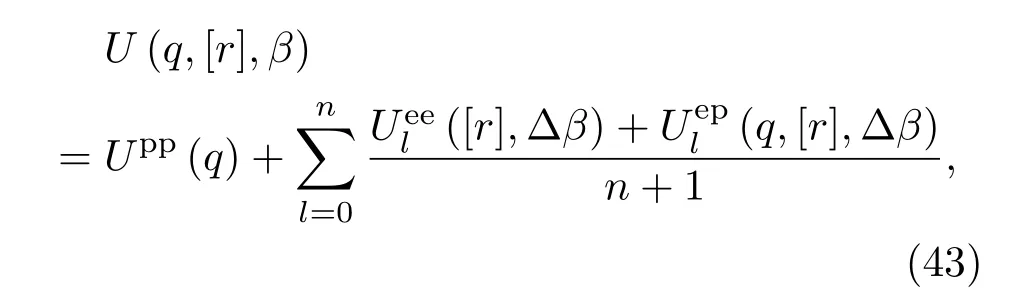
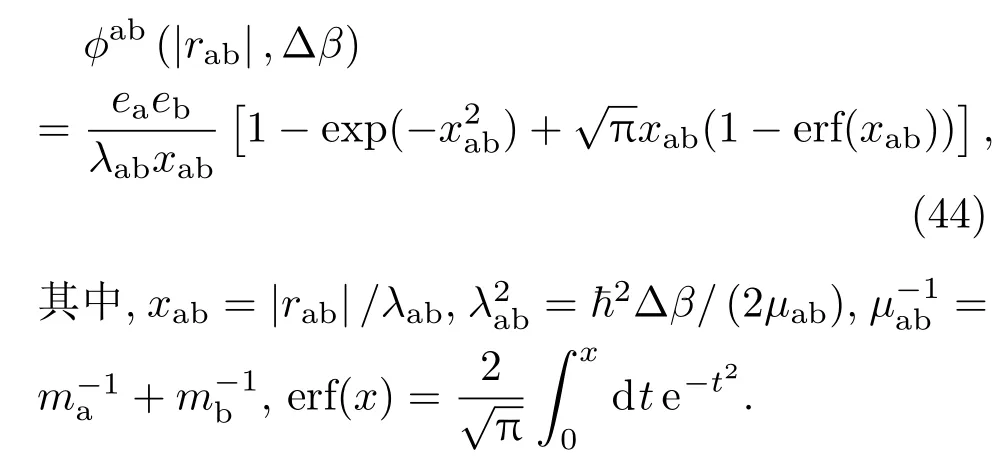
根据统计物理学的热力学公式,可以得到系统能量和压强的表达式.能量的计算公式为βE=−β∂ln Q/∂β,压强公式为βp=∂ln Q/∂V=[α/3V∂lnQ/∂α]α=1.以上计算状态方程的公式中都包含多重积分,不能直接进行计算,但很适合采用标准的蒙特卡罗方法进行数值计算.

3.2.2 DPIMC计算结果

我们对氢等离子体状态方程进行了大量的计算.图17是125000 K温度下的压强随密度的变化,我们将计算结果与其他数值方法进行了比较,图中的QMD表示基于密度泛函理论的量子分子动力学方法[82],RPIMC表示约束路径积分蒙特卡罗方法[77].在低密度下,关联效应和简并效应都较弱,三种数值方法计算的结果符合得很好.但在高密度下,关联效应和简并效应都很强,三种方法计算的结果存在比较大的偏差.QMD计算的压强比两种路径积分方法更高,可能的原因有以下两点:1)在高温下,QMD一般采用无轨道形式,其电子动能算符的密度泛函形式采用Thomas-Fermi模型,该模型高估电子的压强;2)在密度泛函理论中,交换-关联势通常采用对零温电子气的蒙特卡罗模拟结果进行拟合得到的经验形式,其能否准确描述高温电子的交换-关联效应,没有经过检验.两种路径积分的结果也存在偏差,与它们在处理“负符号”问题时所引入的近似有关.

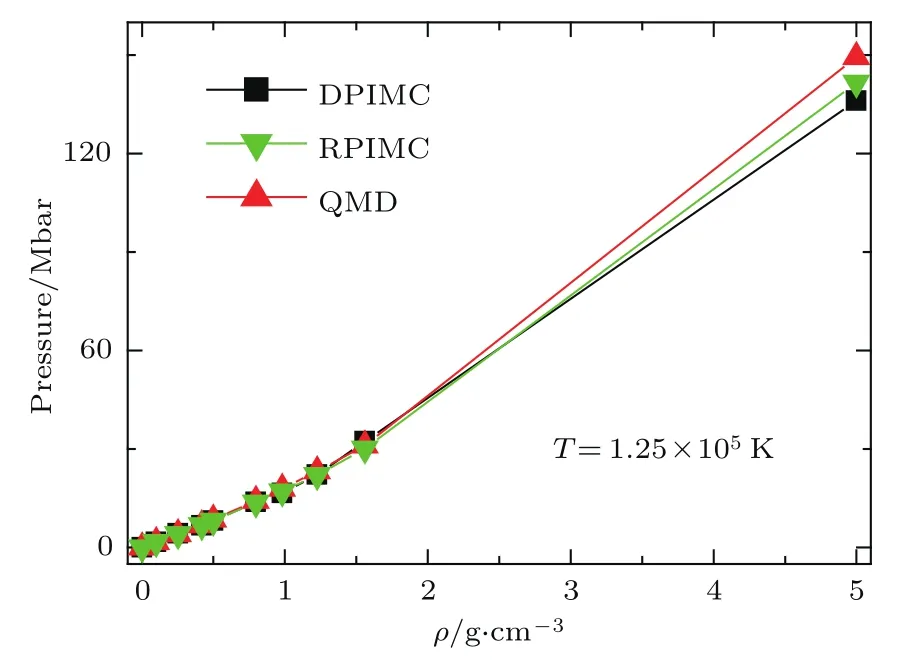
图17 温度T =125000 K时压强与密度的关系(1 bar=105Pa)Fig.17.The pressu re changeswith density at temperature T=125000 K(1 bar=105Pa).

由于QMD与DPIMC计算能量的方式不同,它们计算的能量不能直接比较,在图18中我们比较了DPIMC和RPIMC计算的能量.在大部分温度范围内,两者都符合得很好,只在低温(T=31250 K)下有明显差别,如图18的内插图中最左边的点所示.在该点,Γ=3.37,Θ=0.48,关联和简并效应都不能忽略.这说明DPIMC和RPIMC对关联和简并效应考虑的近似程度是不一样的,在目前的实验技术条件下,在该温度密度下有可能通过精密的实验来进行验证,并为更准确的理论模型提供参考.

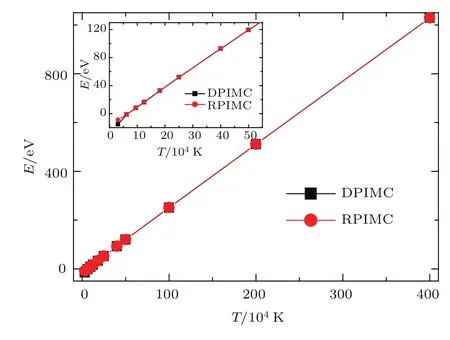
图18 电子数密度为0.05962 A−3时,能量与温度的关系Fig.18.The energy changes with temperatu re at electron density 0.05962 A−3.

4 结 论

针对温稠密物质状态的变化特点,我们介绍了一系列能够计算该区域物态方程的物理模型.建立在液体微扰论基础上的化学图像模型SCVH能够比较好地描述物质从分子到原子、从原子到离子的离解和电离过程.该模型的不足之处是它依赖于粒子之间的详细相互作用势.建立在经验模型基础之上的离化电离平衡模型(IEQ),也是一种近似的化学平衡模型.它也能够比较好地给出物质在过渡区的物态方程.其缺点是该模型有一些经验参数需要由实验来确定.平均原子模型在概念上虽然简单,但它却是描述过渡区原子电离的很好模型.在INFERNO模型中,由于对共振电子态的特殊处理,从而避免了电子电离带来的物理量跳跃.这是INFERNO模型的最大优点.但是该模型也有不足之处,主要是它没有考虑离子的热运动,以及没有考虑其他离子对该离子的关联影响.

第一原理分子动力学和量子蒙特卡罗方法是计算温稠密区物态方程的有效方法.这两种数值模拟方法的最大特点是它能够在量子力学的框架内高效、准确地处理分子离解、原子电离等复杂的物理过程,而且,还能够对温稠密物质的电学性质、光学性质等输运特性做很好的计算.两者共同特点是模拟的粒子数少,计算量大.量子分子动力学方法向高温推广也有一定的困难.量子蒙特卡罗方法向多电子束缚态的低温推广也有一定的困难.

等离子体相变(即PPT)是在温稠密区发现的一个有趣的物理现象,但是在一些分子动力学模拟计算中却没有发现这一现象[83,84],所以有必要从理论和实验上对该问题做进一步地探讨.其次,在温稠密区出现的多元素混合物的相分离现象(如氢氦混合物[85])也是值得进一步研究的课题.这些现象将直接影响人们对行星(如木星)构造的认识.

[1]Xu X S,Zhang W X 1986In troduction tothe Theory of Equation of State(Beijing:Science Press)(in Chinese)[徐锡申,张万箱 1986实用物态方程理论导引(北京:科学出版社)]

[2]Rogers F J,Young D A1997Phys.Rev.E56 5876

[3]Fortov V,Iakubov I,Kh rapak A2006Physics of Strongly Coupled P lasma(Oxford:Ox ford University Press)

[4]Saumon D,Chabrier G,van Horn HM1995Astrophys.J.Suppl.Ser.99 713

[5]Saumon D,Chabrier G 1991Phys.Rev.A44 5122

[6]Saumon D,Chabrier G 1992Phys.Rev.A46 2084

[7]Ju ranek H,Redmer R 2002J.Chem.Phys.117 1768

[8]Kerley G I1986J.Chem.Phys.85 5228

[9]Kerley G I2003Equations of State for Hydrogen and DeuteriumSandia National Laboratories Technical Report No.SAND 2003-3613

[10]Jin F Q 1999In troduction tothe Experimen ts of the Equation of State(Beijing:Science Press)(in Chinese)[经福谦1999实验物态方程导引(北京:科学出版社)]

[11]Rozsnyai BF 1972Phys.Rev.A5 1137

[12]Liberman D A1979Phys.Rev.B20 4981

[13]Zhu X R,Meng X J 2011Acta Phys.Sin.60 093103(in Chinese)[朱希睿,孟续军 2011物理学报 60 093103]

[14]W ilson B,Sonnad V,Sterne P,IsaacsW 2006J.Quan t.Spectrosc.Radiat.Transfer99 658

[15]Penicaud M2009J.Phys.:Condens.Matter21 095409

[16]BarshalomA,Oreg J 2009High Energy Density Physics5 196

[17]Ma G C,Zhang Q L,Lu G 2017Chin.J.High Press.Phys.31 1(in Chinese)[马桂存,张其黎,卢果 2017高压物理学报31 1]

[18]Kress G,Fu rthmu ller J 1996Phys.Rev.B54 11169

[19]Lambert F,C lerouin J,Zerah G 2006Phys.Rev.E73 016403

[20]D river KP,Militzer B2012Phys.Rev.Lett.108 115502

[21]Hu S X,Militzer B,Goncharov V N,Skupsky S 2011Phys.Rev.B84 224109

[22]Vorberger J,Tamb lyn I,Militzer B,Bonev S A2007Phys.Rev.B75 024206

[23]Ju ranek H,Redmer R 2000J.Chem.Phys.112 3780

[24]Kramida A,RalchenkoYu,Reader J,N ISTASD TeamN ISTAtomic Spectra Database(ver.5.3)http://physics.nist.gov/asd[2015-1-2]

[25]NellisW J,van Thiel M,Mitchell AC 1982Phys.Rev.Lett.48 816

[26]Urlin V D,Mochalov MA,Mikhailova OL 1992High Press.Res.8 595

[27]W igner E 1932Phys.Rev.40 749

[28]Kirkwoord J 1933Phys.Rev.44 31

[29]Andersen HC,Chand ler D 1970J.Chem.Phys.53 547

[30]W eeks J D,Chand ler D,Andersen HC 1971J.Chem.Phys.54 5237

[31]W eeks J D,Chand ler D,Andersen HC 1971J.Chem.Phys.55 5422

[32]Hummer D G,Mihalas D 1988Astrophys.J.331 794

[33]Ebeling W,Forster A,Richert W,Hess H1988Physica A150 159

[34]Kerley G I1980J.Chem.Phys.73 469

[35]Kerley G I1980J.Chem.Phys.73 478

[36]Kerley G I1980J.Chem.Phys.73 487

[37]Nellis W J,Mitchell AC,van Thiel M,Devine G J,Trainor R J 1983J.Chem.Phys.79 1480

[38]Boriskov G V,Bykov AI,II’kaev R I,Selemir V D,Simakov G V,Trunin R F,Urlin V D,Shuikin AN,NellisW J 2005Phys.Rev.B71 092104

[39]Knudson MD,Hanson D L,Bailey J E,Hall C A,Asay J R 2001Phys.Rev.Lett.87 225501

[40]Da Silva L B,Celliers P,Collins GW,Budil KS,Holmes N C,Barbee TW,Hammel BA,Kilkenny J D,W allace R J,Ross M,Caub le R,Ng A,Chiu G L B1997Phys.Rev.Lett.78 483

[41]Collins G W,Da Silva L B,Celliers P,Gold D,Foord M,Wallace R,Ng A,W eber S,Budil K,Caub le R 1998Science281 1178

[42]Hicks D G,Boehly TR 2009Phys.Rev.B79 014112

[43]Militzer B,Ceperley D M2000Phys.Rev.Lett.85 1890

[44]Bezkrovniy V,Filinov V S,KrempD,Bonitz M,Sch langes M,Kraeft W D,Levashov P R,Fortov V E 2004Phys.Rev.E70 057401

[45]Caillabet L,Mazevet S,Loubey re P 2011Phys.Rev.B83 094101

[46]Ross M1998Phys.Rev.B58 669

[47]Ma G C,Qi J,W ang M2015Chin.J.Comput.Phys.32 361(in Chinese)[马桂存,齐进,王敏 2015计算物理32 361]

[48]Novikov V G,Ovechkin AA2011Math.Models Comput.Simu lations3 290

[49]BarshalomA,Oreg J 2007High Energy Density Phys.3 12

[50]BarshalomA,Oreg J 2006J.Quan t.Spectrosc.Radiat.Transfer99 35

[51]Kerley G I1987In t.J.Impact.Eng.5 441

[52]YokooM,KawaiN,Nakamura KG,KondoK2008Appl.Phys.Lett.92 051901

[53]Marsh S P 1980Los Alamos Shock Hugoniot Data(Berkeley:University of California Press)

[54]Al’tshu ler L V,Bakanova AA,Dudoladov IP,Dynin E A,Trunin R F,Chekin BS 1981J.Appl.Mech.Tech.Phys.22 145

[55]Jones AH,IsbellW M,Maiden C J 1966J.Appl.Phys.37 3493

[56]Zhu X R,Meng X J,Tian MF 2008Acta Phys.Sin.57 4049(in Chinese)[朱希睿,孟续军,田明峰2008物理学报57 4049]

[57]Militzer B2005J.Low.Temp.Phys.139 739

[58]Zhang Q L,Zhang G M,ZhaoY H,Liu HF 2015Acta Phys.Sin.64 094702(in Chinese)[张其黎,张弓木,赵艳红,刘海风2015物理学报64 094702]

[59]Danel J F,Kazand jian L 2015Phys.Rev.E91 013103

[60]Car R,ParrinelloM1985Phys.Rev.Lett.55 2471

[61]PerdewJP,Burke K,ErnzerhofM1996Phys.Rev.Lett.77 3865

[62]W ang Y,PerdewJ P 1991Phys.Rev.B44 13298

[63]Monkhorst HJ,Pack J D 1976Phys.Rev.B13 5188

[64]Nose S C 1984J.Chem.Phys.81 511

[65]NellisW J,Holmes N C,Mitchell AC,Trainor R J,GovernoG K,Ross M,Young D A1984Phys.Rev.Lett.53 1248

[66]Zhang Q L,ZhaoY H,Ma G C 2014Chin.J.High Press.Phys.28 18(in Chinese)[张其黎,赵艳红,马桂存2014高压物理学报28 18]

[67]Ma G C,PeiW B,W ang M2005Annual Report of ICF272(in Chinese)[马桂存,裴文兵,王敏 2005 ICF科技年报272]

[68]Koenig M,Faral B,Boudenne J,Batani D,Benuzzi A,Bossi S,Remond C,Perrine J P,Temporal M,Atzeni S 1995Phys.Rev.Lett.74 2260

[69]McQueen R,Marsh S 1960J.Appl.Phys.31 1253

[70]Al’tshu ler L,Krupnikov K,Brazhnik MI1958Sov.Phys.JETP7 614

[71]Konstantin D L,Pavel N G,Dorogokupets P I,Igor SS,Shatskiy A,Fei Y W,PashchenkoS V,Seryotkin Y V,HigoY J,Funakoshi K,Ohtani E 2013J.Appl.Phys.113 133505

[72]KuboR 1957J.Phys.Soc.Jpn.12 570

[73]G reenwood D A1958Proc.Phys.Soc.London715 585

[74]Mott N 1984Rep.Prog.Phys.47 909

[75]KorobenkoV N,Rakhel AD 2013Phys.Rev.B88 134203

[76]Ceperley D M1995Rev.Mod.Phys.67 279

[77]Pierleoni C,Ceperley D M,Bernu B,MagroW R 1994Phys.Rev.Lett.73 2145

[78]MagroW R,Ceperley D M,Pierleoni C,Bernu B1996Phys.Rev.Lett.76 1240

[79]Filinov V S,Bonitz M,Ebeling W,Fortov V E 2001P lasmas Phys.Con trolled Fusion43 743

[80]Filinov V S,Fortov V E,Bonitz M,KrempD 2000Phys.Lett.A274 228

[81]Filinov V S,Bonitz M,KrempD,Kraeft W D,Ebeling W,Levashov P R,Fortov V E 2001Con trib.P lasmas Phys.41 135

[82]W ang C,Zhang P 2013Phys.P lasmas20 092703

[83]Holst B,Redmer R,Desjarlais MP 2008Phys.Rev.B77 184201

[84]Redmer R,Ropke G 2010Contrib.Plasma Phys.50 970

[85]Militzer B2013Phys.Rev.B87 014202

PACS:64.10.+h,62.50.–p,91.60.Fe,52.25.KnDOI:10.7498/aps.66.036401

Theoretical study of the equation of state for warmdense matter

Ma Gui-Cun†Zhang Qi-Li Song Hong-Zhou LiQiong Zhu Xi-Rui Meng Xu-Jun

(Institu te of Applied Physics and Compu tational Mathematics,Beijing 100089,China)(Received 23 November 2016;revised manuscript received 26 December 2016)

In this paper,we present in detail various theoretical models for studying the equation of state of warmdense matter,including the fluid variational theory,the chemicalmodel,the ionization equilibriummodel,the average atommodel and INFERNOmodel.The method of calculating the equation of state of a mixture is alsogiven.The results fromthe fi rst principles molecu lar dynamics simu lation and the quantumMonte Carlosimu lation are alsoprovided.Typicalmaterials such as hydrogen,deuterium,helium,xenon,gold,tungsten,etc.are studied in warmdense region by using all themethods,showing the eff ects of dissociation and ionization in the equation of state.

warmdensematter,equation of state,plasma

10.7498/aps.66.036401

†通信作者.E-mail:ma_guicun@iapcm.ac.cn

†Corresponding author.E-mail:ma_guicun@iapcm.ac.cn