三维边界层内定常横流涡的感受性研究∗
沈露予 陆昌根
(南京信息工程大学海洋科学学院,南京 210044)(2016年7月14日收到;2016年10月12日收到修改稿)
三维边界层内定常横流涡的感受性研究∗
沈露予 陆昌根†
(南京信息工程大学海洋科学学院,南京 210044)(2016年7月14日收到;2016年10月12日收到修改稿)
层流向湍流转捩的预测与控制一直是研究的前沿热点问题之一,其中感受性阶段是转捩过程中的初始阶段,它决定着湍流产生或形成的物理过程.但是有关三维边界层内感受性问题的数值和理论研究都比较少;实际工程问题中大部分转捩过程都是发生在三维边界层流中,所以研究三维边界层中的感受性问题显得尤为重要.本文以典型的后掠角45◦无限长平板为例,数值研究了在三维壁面局部粗糙作用下的三维边界层感受性问题,探讨了三维边界层感受性问题与三维壁面局部粗糙长、宽和高之间的关系;然后,考虑在后掠平板上设计不同的三维壁面局部粗糙的分布状态、几何形状、距离后掠平板前缘的位置以及流向和展向设计多个三维壁面局部粗糙对三维边界层感受性问题有何影响;最后,讨论两两三维壁面局部粗糙中心点之间的距离以及后掠角的改变对三维边界层感受性的物理过程将会发生何种影响等.这一问题的深入研究将为三维边界层流中层流向湍流转捩过程的认识和理解提供理论依据.
感受性,三维边界层,壁面局部粗糙
1引 言
边界层内层流向湍流转捩的预测与控制一直是研究的前沿热点问题之一.层流向湍流转捩的物理过程非常复杂,而边界层感受性问题是转捩过程的初始阶段,它决定着层流向湍流转捩的物理机理.早期感受性问题的研究主要集中在二维边界层的情况,而三维边界层内感受性问题的研究较少[1−6];然而,绝大多数的实际转捩过程都发生在三维边界层流中,所以研究三维边界层内的感受性问题更具有重要的实际和理论意义[7].
无限长后掠平板边界层是一种典型的三维边界层流,若在低湍流度的环境下,转捩过程主要由定常横流涡主导;而在高湍流度情况下,转捩过程主要由非定常横流涡主导.实际飞行器的飞行环境大都属于低湍流度的环境,这时三维边界层内的转捩过程一般都取决于定常横流涡;因此,研究三维边界层内诱导产生定常横流涡的物理过程对飞行器的设计和制造是十分重要的.1990年,Bippes和Nitschke-Kowsky[8]通过实验证实后掠翼边界层内的定常横流涡扰动是由壁面局部粗糙激发产生的,而不是自由流中的小扰动引起的.Radeztsky等[9]则在实验中发现后掠翼边界层内的转捩只对三维壁面局部粗糙敏感,对二维壁面局部粗糙不敏感.随后,Radeztsky等[9,10],Deyhle和Bippes[11],Reibert等[12,13]对壁面局部粗糙形状、大小和位置等因素对三维边界层感受性的影响进行了一系列研究.Reibert等[12]还发现在机翼前缘设置的一排壁面局部粗糙时,可以激发出与壁面局部粗糙间距相应波长的横流涡,且横流涡的波长不会大于局部粗糙之间的距离.Fedorov[14],Manuilovich[15],Crouch[16],Choudhari[17],Ng和Crouch[18]通过有限雷诺数方法研究的结果都表明壁面局部粗糙是激发三维边界层内形成定常横流涡的一种机理;但是,有限雷诺数方法忽略了三维边界层非平行性的影响.Betrolotti[19]通过计算证实边界层前缘的非平行性对后掠翼边界层的感受性有着显著的影响.Collis和Lele[20]将计算获得的结果与Crouch[16]以及Choudhari[17]的计算结果比较后发现,忽略非平行性的影响会对后掠翼边界层流中的感受性问题产生较大的影响.Schrader等[21,22]通过直接数值模拟研究了正压梯度情况下三维边界层的感受性问题.最近,Tempelmann等[23]采用直接数值模拟方法和抛物化方程的方法(PSE)计算了壁面局部粗糙作用下后掠翼边界层内的感受性过程,并与Reibert等[12]的实验结果和Ng和Crouch[18]采用有限雷诺数方法计算得到的结果进行了比较,结果是令人满意的.Kurz和Kloker[24]研究了不同几何形状壁面局部粗糙高度对后掠翼边界层内感受性过程的影响,并获得了一些有意义的结果.
为了符合飞行环境下三维边界层感受性的实际情况,本文采用直接数值模拟方法研究了三维壁面局部粗糙作用下非平行三维边界层内的感受性问题,并且通过数值计算确定了三维壁面局部粗糙长、宽和高、位置、形状、多个分布的局部粗糙以及后掠角等因素与三维边界层感受性之间的关系,这将为飞行环境下三维边界层转捩过程的预测和控制的相关研究提供可靠的理论依据.
2控制方程和数值方法
2.1 控制方程
首先选用边界位移厚度δ∗、无穷远来流速度U∞以及流体密度ρ为特征量,将不可压Navier-Stokes方程进行无量纲化,获得无量纲的Navier-Stokes方程为
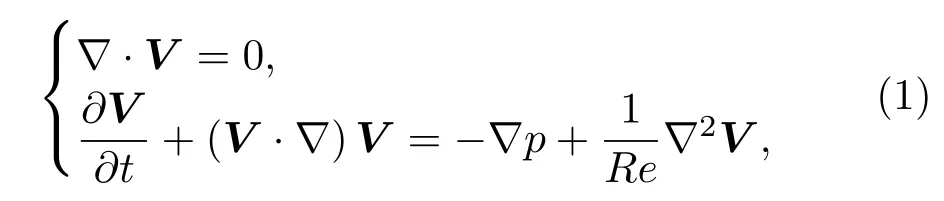
其中:速度V=U+V′,V′={u,v,w}T为扰动速度,基本流U为数值求解Navier-Stokes方程获得的三维边界层基本流的数值解;p为压力;雷诺数为Re=(U∞δ∗)/υ,且υ为流体的运动黏性系数.
2.2 数值方法
基本方程的数值离散为:时间偏导数采用四阶修正后的Runge-Kutta格式进行时间推进[25];空间偏导数采用变间距的紧致有限差分格式,即对流项采用五阶精度迎风紧致有限差分格式,压力梯度项采用六阶精度紧致有限差分,黏性项采用五阶精度紧致有限差分格式离散,展向偏导数均采用傅里叶级数展开,压力方程采用三阶精度的变间距有限差分格式进行迭代求解,具体数值计算格式详见文献[4,6,26].
2.3 计算区域和边界条件
图1所示为本文直接数值模拟的计算区域:流向区域为x∈[0,300],法向区域为y∈[0,14.39],即五倍边界层厚度,展向区域z∈[−Z/2,Z/2],展向宽度Z根据具体情况确定,后掠角ΦBS为无穷远来流U∞方向与x轴之间的夹角.计算网格:x方向、y方向和z方向上的网格数为512×200×16,其中x方向和z方向上采用等间距网格,y方向上采用变间距网格,这样选取网格是为了在壁面附近流场变化剧烈的区域加密网格以便计算获得更准确的流场信息.数值计算选取的雷诺数为Re=1000.

图1 计算区域示意图Fig.1.Computational domain.
上边界条件:p=0;扰动速度为零.下边界条件:采用无滑移条件,则u(x,0)=0,v(x,0)=0,w(x,0)=0,∂p/∂y=0.并在平板上设计壁面局部粗糙.入流条件:扰动速度为零;∂p/∂x=0.出流条件:∂p/∂x=0;扰动速度采用无反射条件[26].展向采用周期性边界条件.
2.4 数值验证
经较长时间(T=2000左右)的数值计算,获得了稳定的三维边界层流向、法向和展向速度(U,V和W)的数值结果,与三维边界层基本流的Falkner-Skan-Cooke理论解比较,发现两者之间是完全符合的,其最大绝对误差为10−5量级,这证明本文构建的直接数值模拟方法具有较高的精度、较好的分辨率以及较稳定的数值计算特性,这为边界层内层流向湍流转捩过程的研究提供了合理的计算平台.
3数值结果与分析
3.1 二维壁面局部粗糙问题
首先,数值研究二维壁面局部粗糙作用下三维边界层内的感受性问题.计算区域的入口雷诺数为Re=220(即Rex=16384,Rex=U∞l/υ,l是到平板前缘的距离),在平板壁面上设计二维壁面局部粗糙,采用线性化的处理方法将二维壁面局部粗糙等效为平板壁面局部区域上的扰动速度,其表达式为

二维壁面局部粗糙放置在流向区域xw∈[6,12]和展向区域zw∈[−Z/2,Z/2];其流向长度、展向宽度以及法向高度分别为L=6.0,Z=50和h=0.004.经较长时间(T>2000)的数值计算,发现在二维壁面局部粗糙作用下三维边界层内流向、法向和展向的扰动速度都趋近于稳定状态,没发现任何小扰动波的演变规律,这说明在二维壁面局部粗糙作用下三维边界层内没发现激发形成小扰动波的物理过程.
3.2 三维壁面局部粗糙问题
在本小节,数值研究了三维壁面局部粗糙作用下三维边界层的感受性问题.计算区域入口雷诺数为Re=220(即Rex=16384),在平板上设计三维壁面局部粗糙[21],采用线性化的处理方法将三维壁面局部粗糙等效为平板壁面局部区域上的扰动速度,其表达式为
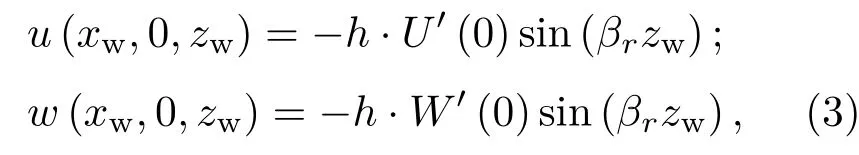
其中:三维壁面局部粗糙的高度h=0.004,U′(0)和W′(0)分别为基本流在壁面上的法向导数值;三维壁面局部粗糙设计在平板壁面上的流向、展向和法向区域分别为xw∈[6,12],zw∈[−Z/2,Z/2]和y∈[0,0.004];并选取三维壁面局部粗糙展向宽度为Zw=31.42以及计算区域的展向宽度Z=Zw,且βr=Zw/2π.
在上述条件下,数值研究了三维壁面局部粗糙作用下三维边界层内被激发产生定常横流涡的物理过程.图2给出了T=2000时三维边界层流中被诱导形成小扰动波的流向小扰动速度最大值(y=0.66)处流向、法向和展向小扰动速度(u,v和w)在xoz平面上的等值线分布.由图2可知,在三维壁面局部粗糙作用下三维边界层内被激发产生的小扰动波的波阵面与流向的夹角为45°;流向和展向小扰动速度明显大于法向扰动速度(约大两个量级),且正负条纹相间,其中白色条纹为正的扰动速度以及黑色条纹为负的扰动速度.

图2 三维边界层内被激发出的小扰动波的速度(u,v和w)在xoz平面的分布Fig.2.Velocity distributions(u,v and w)on the xoz plane of the excited perturbation waves in the threedimensional boundary layer.
图3给出了在y=0.66处三维边界层内被激发产生的不稳定小扰动波的流向小扰动速度沿x和z向的演化过程.由图3可知,三维边界层内被感受出不稳定的小扰动波的流向小扰动速度沿x和z向的演变规律始终保持定常状态.
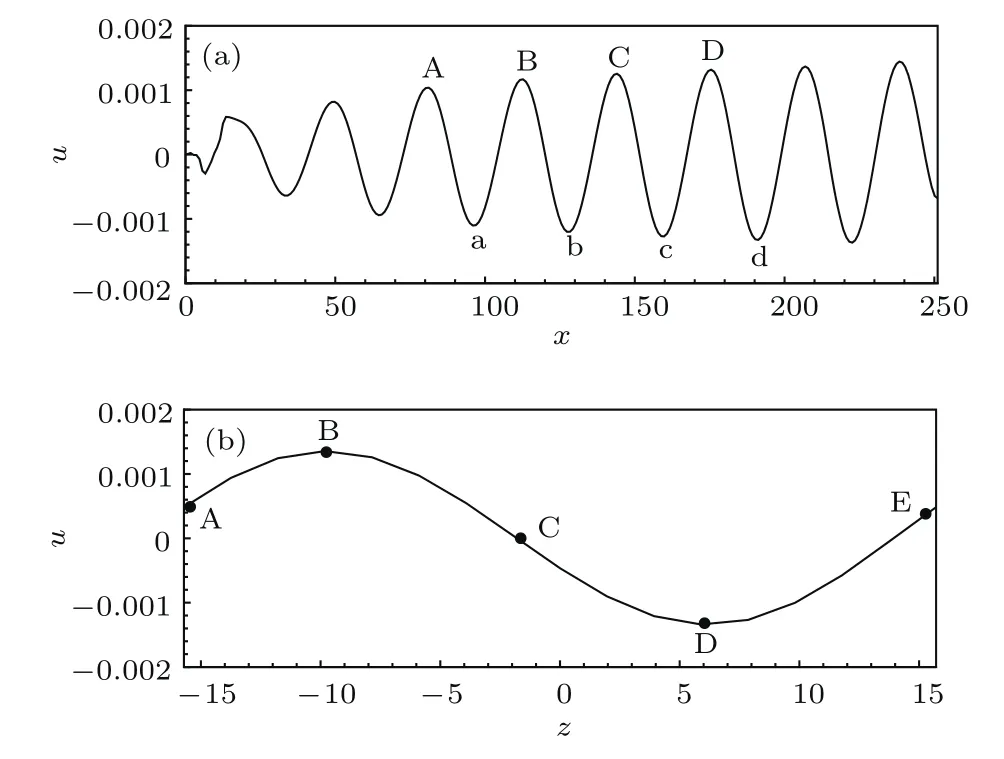
图3 三维边界层内被激发形成小扰动波的流向扰动速度分别沿x和z方向的演变Fig.3.Variations in the x-and z-directions of streamwise velocity of the excited perturbation waves in the three-dimensional boundary layer.
为了验证上述结论,在数值计算过程中分别跟踪图3(a)中所标注的波峰A,B,C和D以及波谷a,b,c和d点的流向位置,发现不稳定的小扰动波的波峰和波谷在任何时刻都保持停留在相同的流向位置上,如图4(a)所示;随后,又分别跟踪图3(b)中所标注的波峰B、波谷D以及点A,C和E的展向位置,发现不稳定的小扰动波的波峰、波谷以及零点位置在任何时刻也都保持在相同的展向位置上,如图4(b)所示.也就是说不稳定的小扰动波的相速度为零,即在三维壁面局部粗糙作用下三维边界层内被感受出的小扰动波为驻波.
再根据图3(a)和图3(b)中三维边界层内被激发产生的小扰动波的流向扰动速度沿x和z向的演化过程,可分别近似数值计算求得驻波的流向和展向平均波数αCF和βCF.具体计算方法为:记录驻波波峰与波峰、波谷与波谷之间的距离,数值计算驻波的波长;依次反复进行,最后取算术平均,获得平均流向和展向波长(或波数).此外,同样还数值计算了后掠角分别为15°,30°,60°和75°时在三维壁面局部粗糙作用下三维边界层内的感受性问题.在不同后掠角情况下,在三维边界层内都能激发出驻波,其数值结果详见表1.
从表1可知,随着后掠角的改变,在三维边界层内被激发产生的驻波的展向波数βCF不发生变化,仅仅只有流向波数αCF发生变化;并且驻波波阵面与流向的夹角θCF始终与后掠角ΦBS完全一致.

图4 小扰动波流向小扰动速度的波峰(实线)和波谷(虚线)等位置随时间t的演变Fig.4.Position variations with time of the peaks and valleys of streamwise velocity of the excited perturbation waves in the three-dimensional boundary layer.

表1 驻波流向和展向平均波数αCF和βCF以及波阵面与流向夹角θCF随后掠角ΦBS的变化Table 1. The angle θCFbetween wave front and streamwise direction,average wave numbers αCFand βCFof the stationary waves varying with the backswept angle ΦBS.
另外,在这里,将三维边界层内被激发出的驻波在局部粗糙中心点处的初始幅值ACFR定义为

其中:uCFR,vCFR和wCFR分别为x,y和z方向上被诱导出的驻波在壁面局部粗糙中心点处的初始扰动速度,且初始扰动速度平方项上的横杠表示时均值.图5给出了三维边界层内被激发出的驻波的初始幅值随后掠角的变化.
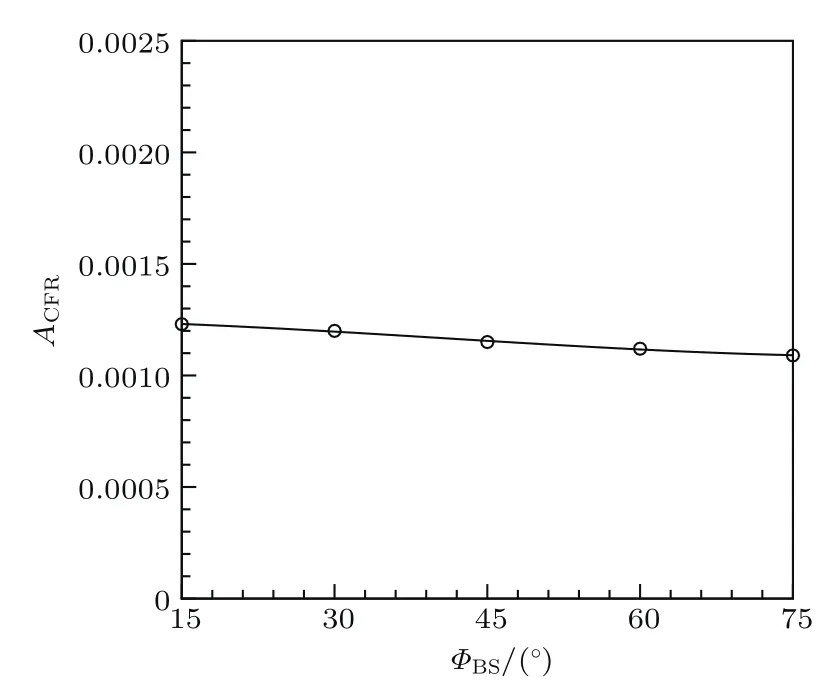
图5 三维边界层内被激发出的驻波的初始幅值随后掠角的变化Fig.5.The initial amplitude of the excited stationary waves in the three-dimensional boundary layer varying with the back-swept angle.
从图5可知,随着后掠角ΦBS的不断增加,在三维壁面局部粗糙作用下三维边界层内被激发出的驻波在局部粗糙中心点处的的初始幅值ACFR呈现缓慢的线性衰减趋势.
最后,在流向长度和法向高度不变的情况下,数值研究三维壁面局部粗糙的展向宽度Zw的变化对三维边界层感受性的影响问题;即选取展向宽度Zw分别为62.83,20.94,15.71和12.57情况下,讨论在三维壁面局部粗糙作用下三维边界层感受性问题的影响.在线性理论的求解过程中,假设驻波的频率等于10−4量级的数值近似等于零,这是因为若取驻波的频率绝对等于零的话在求解线性理论解时会产生明显的数值震荡,经这样近似处理后就能有效地遏制数值震荡,详细结果见表2.由表2可知,在三维壁面局部粗糙作用下三维(后掠角为45°时)边界层内被激发出的驻波的流向和展向平均波长均近似等于Z,即在三维壁面局部粗糙作用下三维边界层内被激发出扰动驻波的流向和展向波长近似等于两两三维壁面局部粗糙展向间距中心点之间的距离,这一结论与Reibert等[12]的实验结论一致.从表2还可知,三维边界层内被激发出的驻波的色散关系与线性理论求得的定常横流涡的色散关系的解也是符合的.
再从表2中选取某一展向波数βCF=0.5的驻波情况,数值计算获得驻波的幅值和相位沿y向的分布,并与线性理论解比较,发现两者之间的也是完全重合的,详细见图6所示.
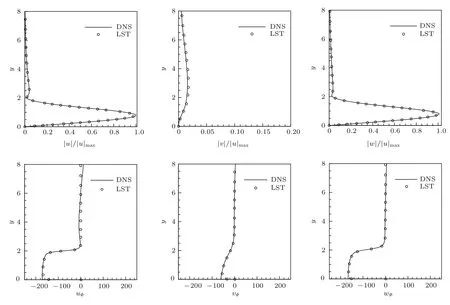
图6 三维边界层内被激发出驻波的扰动速度的幅值|u|,|v|和|w|以及相位uΦ,vΦ和wΦ沿y向的分布(x=125,βCF=0.5)Fig.6.The amplitude|u|,|v|and|w|and phase uΦ,vΦ and wΦ distribution in the y-direction of the excited stationary waves in the three-dimensional boundary layer(x=125,βCF=0.5).

表2 驻波的平均流向波长λx与平均展向波长λz与线性理论解比较Table 2.The average streamwise and spanwise wavelength λxand λzcomparing with the theoretical solutions.
综上所述,在三维壁面局部粗糙作用下三维边界层内感受出的驻波色散关系、幅值和相位的数值结果都与定常横流涡的线性理论解符合,从而证明了在三维壁面局部粗糙作用下三维边界层内被激发的扰动驻波就是定常横流涡,也就是说三维壁面局部粗糙是三维边界层内感受性问题的一种理论机理.
3.3 三维边界层感受性问题与三维局部粗糙结构、位置以及流向个数之间的关系
以展向波数βCF=0.5的驻波情况为例,分别通过改变三维壁面局部粗糙长、宽和高,三维壁面局部粗糙中心点距前缘的距离以及三维壁面局部粗糙的流向分布的个数来分别研究它们与三维边界层感受性问题之间的关系.
3.3.1 三维边界层感受性问题与三维壁面局部粗糙长、宽和高之间的关系
图7给出了在三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的初始幅值ACFR与三维壁面局部粗糙长度L之间的关系,其中图7中的壁面局部粗糙长度L被波长4π/αCF归一化以及被激发出的定常横流涡的初始幅值ACFR被最大幅值Amax归一化.从图7可知,在三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的初始幅值ACFR/Amax与正弦曲线sin(LαCF/4)相重合,即在三维壁面局部粗糙作用下三维边界层内激发出的定常横流涡的初始幅值ACFR/Amax与局部粗糙长度LαCF/(4π)之间呈现正弦曲线变化的关系;且当壁面局部粗糙长度L等于2π/αCF时,能被激发出最大初始幅值的定常横流涡.
图8给出了在三维壁面局部粗糙作用下三维边界层内激发出定常横流涡的初始幅值ACFR/Awmax与三维壁面局部粗糙宽度Zw之间的关系,其中Awmax为边界层内被激发出定常横流涡的最大初始幅值.由图8可知,当Zw<21.0,Zw=21.0和Zw>21.0时,三维边界层内被激发出的定常横流涡的初始幅值分别随三维壁面局部粗糙宽度的增大而增长,直至到三维壁面局部粗糙宽度等于21.0时取得最大值以及随三维壁面局部粗糙宽度的增大而演度成较快衰减的趋势.这一变化过程与Schrader等[21]数值研究三维边界层感受性问题得到的结果一致.
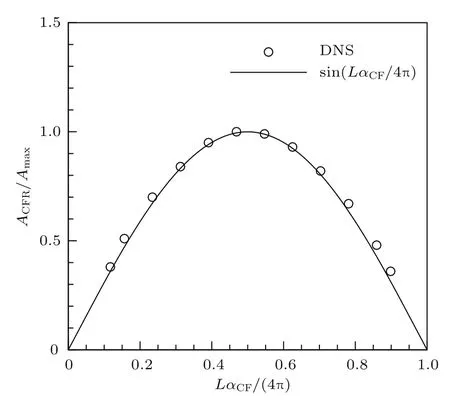
图7 三维边界层内被激发出的定常横流涡的初始幅值与三维局部粗糙长度之间的关系Fig.7.The relation between the initial amplitude of the excited stationary cross- fl ow vortice in the threedimensional boundary layer and three-dimensional localized roughness length.

图8 三维边界层内被激发出的定常横流涡的初始幅值与三维局部粗糙宽度之间的关系Fig.8.The relation between the initial amplitude of the excited stationary cross- fl ow vortice in the threedimensional boundary layer and three-dimensional localized roughness width.
图9给出了在三维壁面局部粗糙作用下三维边界层内激发出的定常横流涡的初始幅值ACFR/A0与壁面局部粗糙高度h之间的关系,其中A0为h=0.01时三维壁面局部粗糙作用下三维边界层内被激发产生的定常横流涡的初始幅值.从图9中可以看出,当无量纲粗糙高度hw≤0.02时,定常横流涡的初始幅值与局部粗糙高度呈现线性增长关系;当h>0.02时,定常横流涡的初始幅值随局部粗糙高度的增长几乎呈现非线性关系;该结论与Kurz和Kloker[24]数值计算的结果符合.
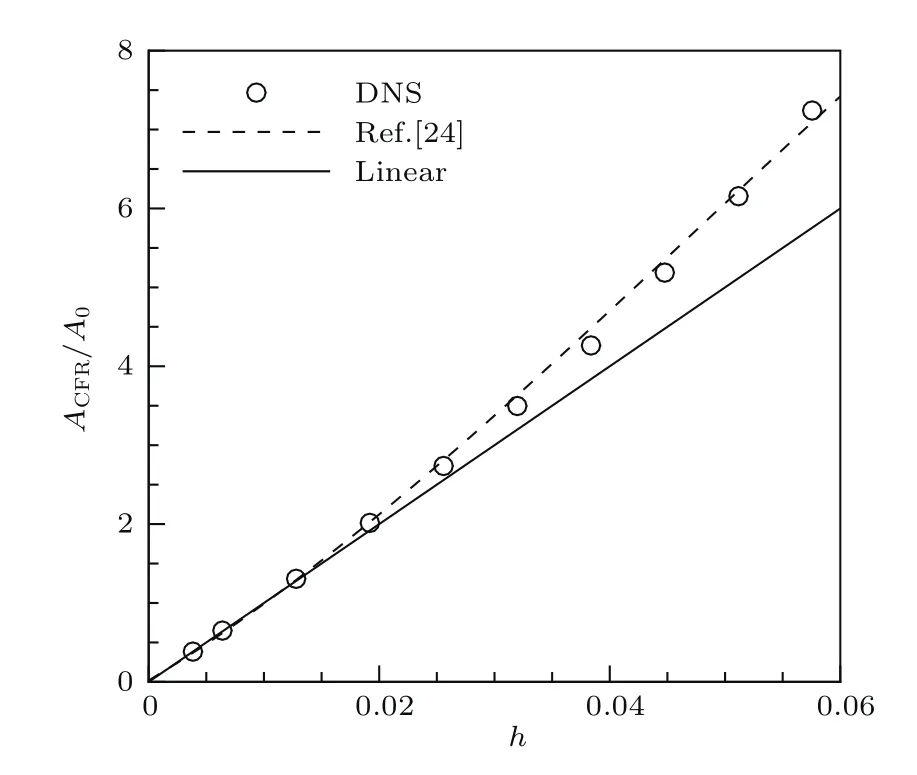
图9 三维边界层内被激发出的定常横流涡的初始幅值与三维局部粗糙高度之间的关系Fig.9.The relation between the initial amplitude of the excited stationary cross- fl ow vortice in the threedimensional boundary layer and three-dimensional localized roughness height.
3.3.2 三维边界层感受性问题与三维壁面局部粗糙位置以及流向个数之间的关系
在三维壁面局部粗糙长、宽和高不变的情况下,仅改变三维壁面局部粗糙中心点距前缘的距离或位置(简称三维壁面局部粗糙位置)来研究三维边界层内被激发出的定常横流涡的初始幅值与三维壁面局部粗糙位置之间的关系.图10给出了三维边界层内被激发出的定常横流涡的初始幅值ACFR/A0随三维壁面局部粗糙位置Rex的变化,其中A0为Rex=1282时在三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的初始幅值.
从图10可以看出,在1002<Rex<5502的范围内,三维边界层内被激发出的定常横流涡的初始幅值随着三维壁面局部粗糙位置逐渐向下游移动而渐渐衰减,而三维壁面局部粗糙中心点距前缘距离越近所能激发三维边界层内产生的定常横流涡的初始幅值越大.

图10 三维边界层内被激发的定常横流涡初始幅值与三维局部粗糙位置Rex的关系Fig.10.The relation between the initial amplitude of the excited stationary cross- fl ow vortice in the threedimensional boundary layer and three-dimensional roughness location Rex.
若在平板壁面上沿流向分别均匀放置多个三维壁面局部粗糙(n=1,3,5,···,15),且两两三维壁面局部粗糙中心点之间的流向间隔等于三维壁面局部粗糙的展向宽度Zw时,研究在流向多个分布的三维壁面局部粗糙作用下三维边界层内的感受性问题.图11给出了在流向设计多个三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的初始幅值ACFR/An=1与三维壁面局部粗糙在流向分布的个数n之间的关系,其中An=1代表单个三维壁面局部粗糙作用下边界层内被激发出的定常横流涡的初始幅值.从图11可知,当流向三维壁面局部粗糙个数n≤5,5<n<11和n≥11时,分别随着流向三维壁面局部粗糙个数的增加而三维边界层内被激发出的定常横流涡的初始幅值增长较快、缓慢增长和渐渐趋于平稳演化的发展趋势.
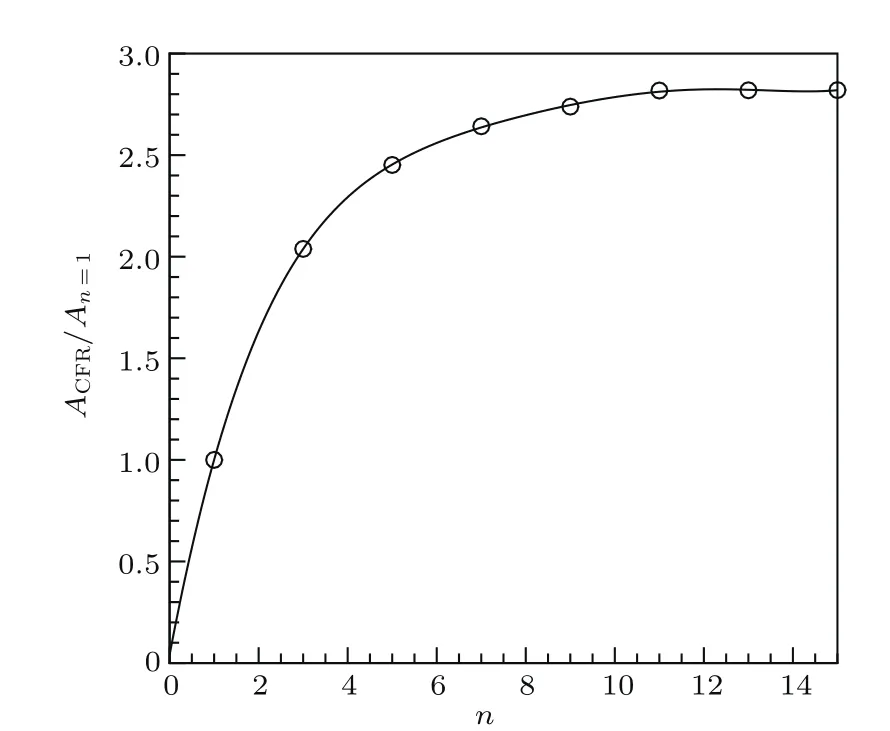
图11 三维边界层内被激发的定常横流涡初始幅值与流向三维局部粗糙个数之间的关系Fig.11.The relation between the initial amplitude of the excited stationary cross- fl ow vortice in the threedimensional boundary layer and three-dimensional roughness numbers.
3.4 三维局部粗糙展向宽度的改变将会对三维边界层内感受性问题产生的影响
计算区域:流向区域x∈[0,300];法向区域y∈ [0,14.39]和展向区域z∈ [−Z/2,Z/2],且Z = 62.83.后掠角为45°. 计算网格数:512×200×32;三维壁面局部粗糙的展向分布为zw∈[−Zw/2,Zw/2],且Zw=31.42,即Zw≤Z.
首先,讨论三维壁面局部粗糙的展向宽度的变化将会对三维边界层内被激发出的定常横流涡产生什么影响.图12给出了在三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的流向扰动速度沿x向的演化.
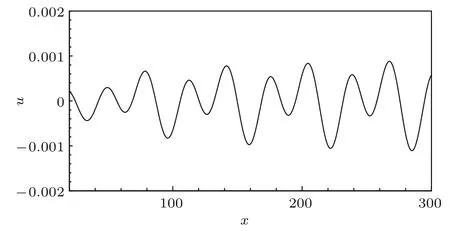
图12 三维边界层内被激发的定常涡扰动速度u沿x向的演变Fig.12.The x-direction evolution of the excited stationary cross- fl ow vortices in the three-dimensional boundary layer.
通过快速傅里叶变换,可以从图12中提取获得两种不同流向和展向波长的不稳定的定常横流涡,它们的流向或展向波长分别为62.83和31.42.也就是说三维边界层内被激发出的一种不稳定的定常横流涡,其流向或展向波长等于两两三维壁面局部粗糙中心点之间的展向间距Z,另一种不稳定的定常横流涡的流向和展向波长等于三维壁面局部粗糙的展向宽度Zw,详细结果如图13(a)和图13(b).
其次又将三维壁面局部粗糙的展向宽度Zw分别改为15.71和12.57,且两两三维壁面局部粗糙中心点之间的展向间距Z仍保持不变的情况下,同样可通过傅里叶变换的方法分别提取获得了三维边界层内被激发出的两种不同的定常横流涡:一种不稳定的定常横流涡的流向和展向波长仍等于两两三维壁面局部粗糙中心点之间的展向间距Z,且该不稳定的定常横涡的色散关系相同;但是,此时三维边界层内被激发出的不稳定的定常横涡的幅值将随三维壁面局部粗糙的展向宽度的减少而逐渐衰减;另一种定常横流涡的流向和展向波长仍等于三维壁面局部粗糙的展向宽度Zw,且对应于三维壁面局部粗糙的展向宽度为15.71和12.57时分别为中性的和稳定的定常横流涡,详细如图13(a),图13(c)和图13(d)所示.也就是说,三维壁面局部粗糙的展向宽度的大小不同能诱导三维边界层内产生不同性质的定常横流涡,即不稳定的、中性的和稳定的定常横流涡.

图13 三维边界层内被激发的(a)λ=Z不稳定波,(b)λ=31.42不稳定的,(c)λ=15.71中性的以及(d)λ=12.57稳定的定常横流涡的流向扰动速度沿x向的演变Fig.13.The x-direction evolutions of the excited stationary cross- fl ow vortices in the three-dimensional boundary layer:(a)λ=Z the unstable wave;(b)λ=31.42the unstable wave;(c)λ=15.71the neutral wave;(d)λ=12.57the stable wave.
随后,再通过改变三维壁面局部粗糙的展向宽度Zw,来研究三维边界层内被激发的定常横流涡的初始幅值ACFR与三维局部粗糙展向宽度Zw之间的关系,详细见图14.从图14中可以看出,三维边界层内被激发出的两种定常横流涡的初始幅值都随着三维壁面局部粗糙展向宽度Zw的增加而增长,其中三维边界层内被激发的流向和展向波长等于Zw的定常横流涡的初始幅值明显大于流向和展向波长都等于Z的定常横流涡的初始幅值.当Zw≤30时,流向和展向波长等于Zw的定常横流涡的初始幅值呈现出快速增长的趋势;当Zw>30时,其增长趋势逐渐变缓.当Zw≤12时,流向和展向波长等于Z的定常横流涡的初始幅值展现出缓慢增长的趋势;当Zw>12时,其增长趋势逐渐加快.
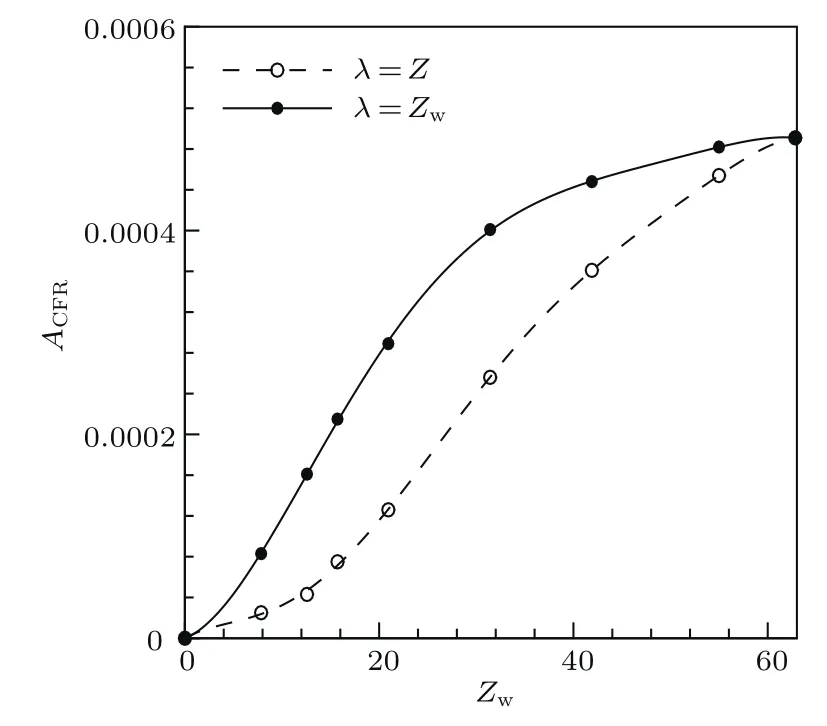
图14 定常横流涡的初始幅值ACFR与三维壁面局部粗糙展向宽度Zw之间的关系Fig.14. The relation between the initial amplitude ACFRof the excited stationary cross- fl ow vortice in the three-dimensional boundary layer and threedimensional localized roughness width Zw.
紧接着,又研究了在展向方向设计两个三维壁面局部粗糙作用下三维边界层内被激发产生定常横流涡的物理过程.在平板上均匀设计两个展向宽度Zw=15.71相等的三维壁面局部粗糙,且两两局部粗糙中心点之间的展向间距为Zd=Z/2.在这样的条件下,能够在三维边界层内激发产生两个流向和展向波长分别都等于Zd和Zw的定常横流涡.然而,又讨论在平板上均匀设计两个不同展向宽度分别为Zw1=15.71和Zw2=12.57情况下的三维壁面局部粗糙,且两两局部粗糙中心点之间的展向间距仍为Zd=Z/2;这时,能够在三维边界层内激发出三个不同波长的定常横流涡:一种是流向和展向波长等于Zd的定常横流涡;而另外两个定常横流涡的流向和展向波长分别都等于三维壁面局部粗糙的展向宽度Zw1和Zw2.

图15 三维边界层内激发出的定常横流涡的流向扰动速度沿x向的演化 (a)Zd=62.83的不稳定波;(b)Zw=31.42不稳定波;(c)Zw=15.71的中性波;(d)Zw=7.86的稳定波Fig.15. The x-direction evolutions of the excited stationary cross- fl ow vortices in the three-dimensional boundary layer:(a)Zd=62.83the unstable wave;(b)Zw=31.42the unstable wave;(c)Zw=15.71the neutral wave;(d)Zw=7.86the stable wave.
最后,选取计算区域的展向宽度为Z =125.66,并在平板上分别均匀设计两个三维壁面局部粗糙、且展向宽度Zw相等,即Zw分别取31.42,15.71和7.86,并使两两局部粗糙中心点之间的展向间距保持不变(Zd=62.83);在上述基础上,两两三维壁面局部粗糙作用下三维边界层内能够激发出流向和展向波长都分别等于Zd和Zw的定常横流涡:一种是流向和展向波长等于Zd的不稳定的定常横流涡,且色散关系相同;但是,幅值随着三维壁面局部粗糙展向宽度的减少而呈现衰减的演化规律;以及分别对应三维壁面局部粗糙展向宽度为31.42,15.71和7.86而获得了另一种流向和展向波长等于Zw的不稳定的、中性的和稳定的定常横流涡;其数值计算获得的定常横流涡的波长分别与Zd和Zw之间存在的最大相对误差大约为10−3量级,详细如图15和表3所示.由此可见,可通过改变三维壁面局部粗糙的展向宽度来避免三维边界层内诱导不稳定定常横流涡的发生,从而达到抑制三维边界层转捩的目的.
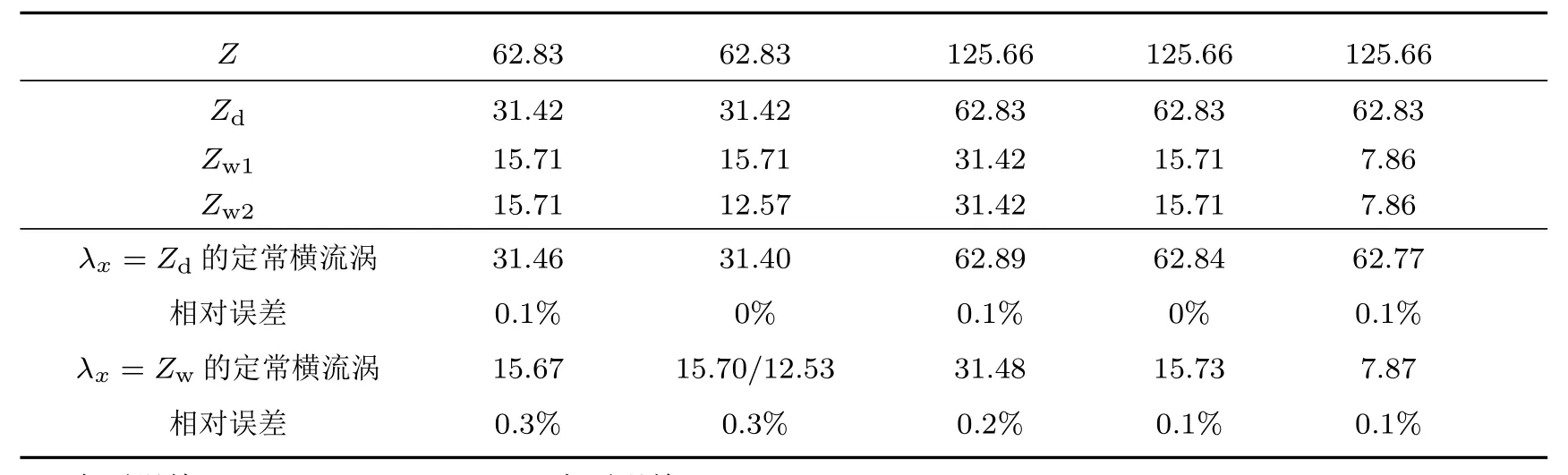
表3 三维边界层内激发的定常横流涡的平均流向波长λxTable 3.The average streamwise wavelength λxof the excited stationary cross- fl ow vortices in the threedimensional boundary layer.
3.5 三维边界层内感受性与后掠角之间的关系
在Z=62.83和Zw=31.42的情况下,通过改变后掠角来研究三维壁面局部粗糙作用下三维边界层内激发出的定常横流涡将产生什么作用.经数值计算获得了三维边界层内被激发形成的定常横流涡的平均流向波数αCF、平均展向波数βCF以及波面与流向之间的夹角θCF,其结果详见表4.从表4中可见,随着后掠角度ΦBS的不断增大,其三维边界层内被激发产生的定常横流涡的平均展向波数βCF保持恒定;但是,平均流向波数αCF随着后掠角ΦBS的不断增大而增大;并且三维边界层内所激发出的定常横流涡的波阵面与流向之间的夹角θCF与后掠角ΦBS符合一致,其两者之间产生的最大相对误差约为0.7%;此外,随着后掠角的不断增大,三维边界层内所激发出的两种定常横流涡的初始幅值的大小将逐渐缓慢衰减,详细如图16所示.
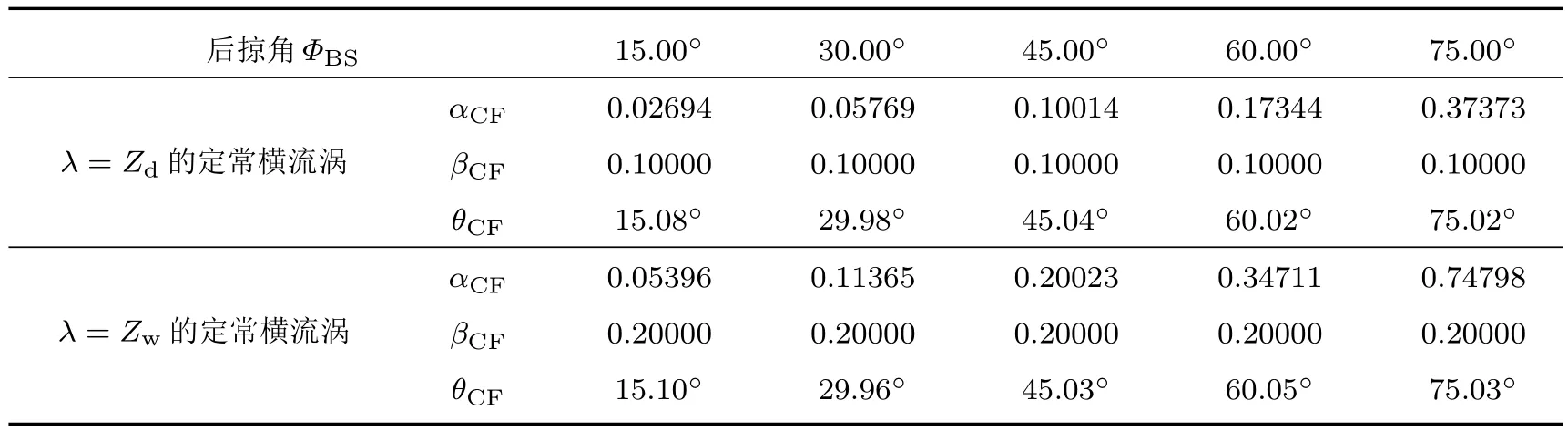
表4 三维边界层内激发的定常横流涡的平均流向波数αCF、平均展向波数βCF以及波面与流向夹角θCF随后掠角ΦBS的变化Table 4.The angle θCFbetween wave front and streamwise direction,average wave numbers αCFand βCF of the stationary cross- fl ow vortices varying with the back-swept angle ΦBS.
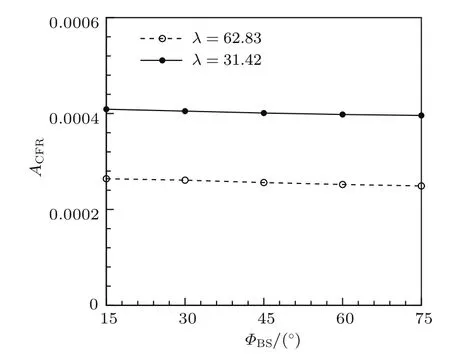
图16 三维边界层内被激发出的定常横流涡的初始幅值随后掠角的变化Fig.16.The initial amplitude of the excited crossfl ow vortices in the three-dimensional boundary layer varying with the back-swept angle.
3.6 三维壁面局部粗糙的几何形状的改变对三维边界层内感受性的影响
在平板上分别设计流向和展向截面几何形状为正弦曲线、矩形和三角形的三维壁面局部粗糙,来探索三维壁面局部粗糙的几何形状的改变对三维边界层内感受性的影响.不同几何形状的三维壁面局部粗糙都被设计在相同的流向区域xw∈[6,12]和展向区域zw∈[−Z/2,Z/2],且Z=31.42,计算网格数为512×200×16;计算区域包括流向区域x∈[0,300]、法向区域y∈[0,14.39]和展向区域z∈[−Z/2,Z/2].
首先,研究三维壁面局部粗糙展向几何形状的变化对三维边界层感受性的影响.下面,分别研究在展向几何形状为矩形、正弦和三角形的三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的物理过程.其中三维壁面局部粗糙的流向几何形状均为矩形,且保持三维壁面局部粗糙具有相同的体积,再采用线性化的处理方法将三维壁面局部粗糙等效为平板壁面局部区域上的扰动速度,其表达式为:


从图17可以看出,无论三维壁面局部粗糙的展向几何形状是矩形、正弦还是三角形,其在三维边界层内被激发出的定常横流涡的幅值、波长、相位以及演变的物理规律几乎完全相同,也就是说在三维壁面局部粗糙的流向几何形状均为矩形以及保持三维壁面局部粗糙具有相同的体积的条件下,仅改变三维壁面局部粗糙的展向几何形状对三维边界层内诱导的定常横流涡无影响.

图17 不同展向几何形状三维壁面局部粗糙激发出的定常横流涡沿流向的演化Fig.17.The x-direction evolutions of the stationary cross- fl ow vortices excited by the three-dimensional roughness with di ff erent spanwise shapes.
其次,研究三维壁面局部粗糙流向几何形状的变化对三维边界层感受性的影响.分别研究在流向几何形状为矩形、正弦和三角形的三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的物理过程,其中上述三维壁面局部粗糙的展向几何形状均为正弦形分布,且保持三维壁面局部粗糙具有相同的体积,再采用线性化的处理方法将三维壁面局部粗糙等效为平板壁面局部区域上的扰动速度,其表达式为:

上式中的x1和x2分别为三维壁面局部粗糙流向位置的起点和终点;xw∈[x1,x2],x1=6,x2=12.从图18可以看出,无论三维壁面局部粗糙的流向几何形状是矩形、正弦形还是三角形,其在三维边界层内激发出的定常横流涡的波长、相位以及演变规律几乎完全符合;仅被激发出的定常横流涡的幅值稍有变化,其中流向几何形状为矩形的三维壁面局部粗糙激发出的定常横流涡的幅值最大,其次是正弦形以及最小为三角形.也就是说在三维壁面局部粗糙的展向几何形状均为正弦形以及保持三维壁面局部粗糙具有相同的体积的条件下,仅改变三维壁面局部粗糙的流向几何形状对三维边界层内诱导的定常横流涡的幅值产生一定影响外,其他参数无影响.
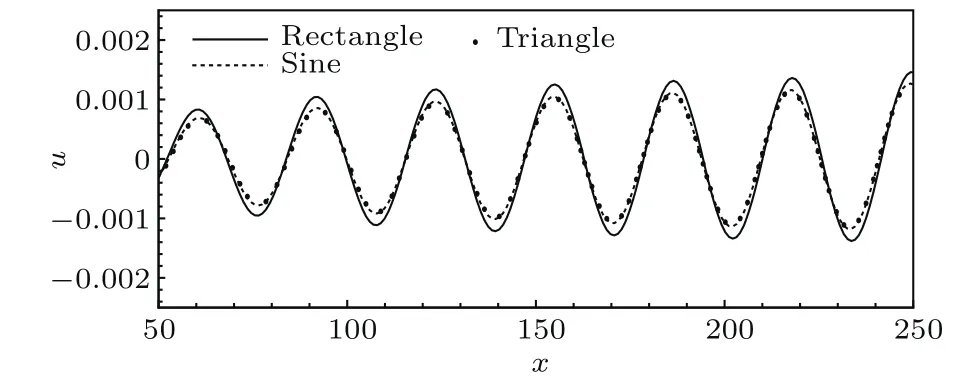
图18 不同流向几何形状三维壁面局部粗糙激发出的定常横流涡沿流向的演化Fig.18.The x-direction evolutions of the stationary cross- fl ow vortices excited by the three-dimensional roughness with di ff erent streamwise shapes.
随后,我们在不改变三维壁面局部粗糙几何形状的情况下,研究具有相同几何形状的壁面凹凸的三维壁面局部粗糙对三维边界层感受性过程的作用.在壁面上设计展向几何形状为正弦、流向几何形状为矩形的壁面局部凹凸,其数学表达式为(6)式,分别取三维壁面局部凹凸高度h为0.004和−0.004,经数值计算发现,在三维边界层内被激发出的定常横流涡沿流向的演化结果,如图19所示.从图19中可以看出,展向几何形状为正弦、流向几何形状为矩形的三维壁面局部凹凸粗糙作用下三维边界层内激发出的定常横流涡具有相同的演化规律,且定常横流涡的幅值和波长相等,惟一不同的是相位相反而已.若在壁面上分布设计展向几何形状为矩形和三角形,且流向几何形状均为矩形的壁面局部凹凸的情况下,获得了与在壁面上设计展向几何形状为正弦、流向几何形状为矩形的壁面局部凹凸的结果相同.
最后,我们研究在壁面上设计流向和展向几何形状均为正弦的壁面局部凹凸粗糙,其数学表达式为(9)式,分别取三维壁面局部凹凸高度为0.006和−0.006.经数值计算发现,在三维边界层内被激发出的定常横流涡沿流向的演化结果,如图20所示.从图20中可以看出,流向和展向几何形状为正弦形的三维壁面局部凹凸粗糙作用下三维边界层内激发出的定常横流涡具有相同的演化规律,且定常横流涡的幅值和波长相等,唯一不同的是相位相反而已.若在壁面上分布分别设计流向和展向几何形状为矩形和三角形壁面局部凹凸粗糙的情况下,获得了与在壁面上设计流向和展向几何形状为正弦形的壁面局部凹凸粗糙的结果相同.也就是说,可以通过合理设计三维壁面局部粗糙的凹凸结构来达到延迟三维边界层内转捩过程的发生.

图19 展向几何形状为正弦的三维壁面局部凹凸激发出的定常横流涡沿流向的演化,h=0.004(实线),h=−0.004(虚线)Fig.19.The x-direction evolutions of the stationary cross- fl ow vortices excited by the three-dimensional concave and convex with sine spanwise shapes:h=0.004(solid line),h=−0.004(dashed line).
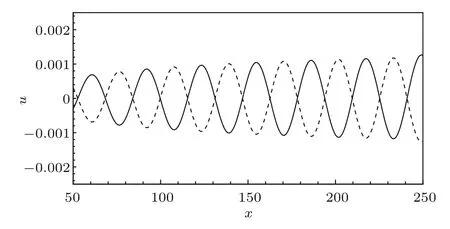
图20 流向几何形状为正弦的三维壁面局部凹凸激发出的定常横流涡沿流向的演化,h=0.006(实线),h=−0.006(虚线)Fig.20.The x-direction evolutions of the stationary cross- fl ow vortices excited by the three-dimensional concave and convex with sine streamwise shapes:h=0.006(solid line),h=−0.006(dashed line).
4结 论
本文采用直接数值模拟方法,研究在壁面局部粗糙作用下诱导三维平板边界层内产生感受性过程的物理问题,获得了如下结论.
1)在二维壁面局部粗糙作用下无法在三维边界层内激发出定常横流涡.在三维壁面局部粗糙作用下三维边界层内能感受出的定常横流涡,就是说三维壁面局部粗糙是诱导三维边界层内感受性的一种物理机理.
2)在三维壁面局部粗糙作用下三维边界层内被激发出的定常横流涡的初始幅值随三维壁面局部粗糙长度之间的关系,满足正弦函数的演变规律;当三维局部粗糙宽度分别小于、等于以及大于21.0时,三维边界层内被激发出的定常横流涡的初始幅值分别随着三维壁面局部粗糙宽度的增大而快速增长,直至到等于21.0时获得最大值以及再随着局部粗糙宽度的增大而演变为较快衰减的趋势;当三维壁面局部粗糙高度分别小于、等于和大于0.02时,三维边界层内被激发出的定常横流涡初始幅值分别与局部粗糙高度呈现线性和非线性增长的关系.
3)当三维壁面局部粗糙的中心点距前缘流向的距离越近时,所能激发三维边界层内形成定常横流涡的初始幅值就越大,反之越小.当流向三维壁面局部粗糙个数n≤5,5<n<11和n≥11时,分别随着三维壁面局部粗糙个数的增加三维边界层内被激发出定常横流涡的初始幅值增长较快、缓慢增长以及趋于平稳的状态.
4)当三维壁面局部粗糙的展向宽度小于计算域的展向区域时,三维边界层内能够被激发出两种定常横流涡:一种是不稳定的定常横流涡,且流向和展向波长等于两两三维壁面局部粗糙中心点之间的展向间距;而另一种定常横流涡可能是属于不稳定的、中性的以及稳定的特征,这一属性取决于三维壁面局部粗糙展向宽度的大小,并且流向和展向波长都等于三维壁面局部粗糙的展向宽度.
5)当三维壁面局部粗糙的展向宽度等于计算域的展向区域时,随着后掠角的改变,定常横流涡的展向波数(或波长)不发生任何变化,仅流向波数(或波长)发生变化,且三维边界层内所激发出的定常横流涡的波阵面与流向之间的夹角与后掠角一致,其幅值呈缓慢的线性衰减趋势.当三维壁面局部粗糙的展向宽度小于计算域的展向区域时,随着后掠角的不断增大,三维边界层内所激发出的两种定常横流涡初始幅值的大小将缓慢衰减,三维边界层内被激发产生的定常横流涡的平均展向波数保持恒定,而平均流向波数将不断增大,且三维边界层内所激发出的定常横流涡的波阵面与流向之间的夹角与后掠角一致.
6)在平板上均匀设计两个不同展向宽度的三维壁面局部粗糙作用下能够在三维边界层内激发出三个不同波长的定常横流涡:一种是不稳定的定常横流涡,且流向和展向波长等于两两三维壁面局部粗糙中心点之间的距离;而另外两个定常横流涡的流向和展向波长分别都等于两个不同三维壁面局部粗糙的展向宽度,且这两个定常横流涡是否属于不稳定的、中性的还是稳定的特征,这一属性取决于三维壁面局部粗糙展向宽度的大小.
7)无论三维壁面局部粗糙的展向形状如何改变,在保持三维壁面局部粗糙体积相同的条件下,三维边界层内被激发出的定常横流涡的波长、相位以及演变的物理规律几乎完全符合;只有当改变三维壁面局部粗糙的流向几何形状对才会对三维边界层内诱导的定常横流涡的幅值产生一定的影响外,对其他物理参数不产生任何影响.
8)无论在流向和展向是什么几何形状的三维壁面局部凹凸粗糙作用下,三维边界层内激发出的定常横流涡的幅值、波长以及演化过程都是相同的,唯一不同的是相位相反.
另外,对于具有带曲率的壁面以及流向压力梯度对三维边界层内感受性过程的影响问题将是我们下一步研究的重点.
[1]Saric W S,Reed H L,White E B 2003 Annu.Rev.Fluid.Mech.35 413
[2]Shen L Y,Lu C G 2016 Appl.Math.Mech.37 349
[3]Shen L Y,Lu C G 2016 Appl.Math.Mech.37 929
[4]Lu C G,Shen L Y 2015 Acta Phys.Sin.64 224702(in Chinese)[陆昌根,沈露予 2015物理学报 64 224702]
[5]Lu C G,Shen L Y 2016 Acta Phys.Sin.65 194701(in Chinese)[陆昌根,沈露予 2016物理学报 65 194701]
[6]Shen L Y,Lu C G 2016 Appl.Math.Mech.37 1145(in Chinese)[沈露予,陆昌根2016应用数学与力学 37 1145]
[7]Xu G L,Fu S 2012 Adv.Mech.42 262(in Chinese)[徐国亮,符松2012力学进展42 262]
[8]Bippes H,Nitschke-Kowsky P 1990 AIAA J.28 1758
[9]Radeztsky Jr R H,Reibert M S,Saric W S 1994 AIAA P.2373
[10]Radeztsky R H,Reibert M S,Saric W S 1999 AIAA J.37 1370
[11]Deyhle H,Bippes H 1996 J.Fluid.Mech.316 73
[12]Reibert M S,Saric W S,Carrillo Jr R B,et al.1996 AIAA P.0184
[13]Reibert M S,Saric W S 1997 AIAA P.1816
[14]Fedorov A V 1988 J.Appl.Mech.Tech.Phys.29 643
[15]Manuilovich S V 1989 Fluid.Dyn.24 764
[16]Crouch J D 1993 AIAA P.0074
[17]Choudhari M 1994 Theor.Comp.Fluid.Dyn.6 1
[18]Ng L L,Crouch J D 1999 Phys.Fluid.11 432
[19]Bertolotti F P 2000 Phys.Fluid.12 1799
[20]Collis S S,Lele S K 1999 J.Fluid.Mech.380 141
[21]Schrader L U,Brandt L,Henningson D S 2009 J.Fluid.Mech.618 209
[22]Schrader L U,Brandt L,Mavriplis C,et al.2010 J.Fluid.Mech.653 245
[23]Tempelmann D,Schrader L U,Hani fiA,et al.2012 J.Fluid.Mech.711 516
[24]Kurz H B E,Kloker M J 2014 J.Fluid.Mech.755 62
[25]Shen L Y,Lu C G,Wu W G,Xue S F 2015 Add.Appl.Math.Mech.7 180
[26]Lu C G,Cao W D,Zhang Y M,Guo J T 2008 P.Nat.Sci.18 873
PACS:47.20.Pc,47.20.—k,47.27.ekDOI:10.7498/aps.66.014703
*Project supported by the National Natural Science Foundation of China(Grant No.11472139),the Startup Foundation for Introducing Talent of NUIST(Grant No.2016r046),the Priority Academic Program Development of Jiangsu Higher Education Institutions,China,and Marine Environment Detection of Engineering Technology Research Center of Jiangsu Province,China.
†Corresponding author.E-mail:cglu@nuist.edu.cn
Receptivity of the steady cross- fl ow vortices in three-dimensional boundary layer∗
Shen Lu-Yu Lu Chang-Gen†
(School of Marine Science,Nanjing University of Information Science and Technology,Nanjing 210044,China)(Received 14 July 2016;revised manuscript received 12 October 2016)
The prediction and control of the laminar-turbulent transition are always one of the most concerned frontiers and hot topics.Receptivity is the initial stage of the laminar-turbulent transition process in the boundary layer,which decides the physical process of the turbulent formation.To date,the researches of receptivity in the three-dimensional boundary layer are much less than those in the two-dimensional boundary layer;while most of the real laminar-turbulent transition in practical engineering occurs in three-dimensional boundary layers.Therefore,receptivity under the threedimensional wall local roughness in a typical three-dimensional boundary layer,i.e.,a 45◦back swept in fi nite fl at plate,is numerically studied.And a numerical method for direct numerical simulation(DNS)is constructed in this paper by using fourth order modi fi ed Runge-Kutta scheme for temporal march and high-order compact fi nite di ff erence schemes based on non-uniform mesh for spatial discretization:the convective term is discretized by fi fth-order upwind compact finite di ff erence schemes;the pressure term is discretized by sixth-order compact fi nite di ff erence schemes;the viscous term is discretized by fi fth-order compact fi nite di ff erence schemes;and the pressure equation is solved by third-order finite di ff erence schemes based on non-uniform mesh.As a result,the excited steady cross- fl ow vortices are observed in the three-dimensional boundary layer.In addition,the relations of three-dimensional boundary-layer receptivity with the length,the width,and the height of three-dimensional wall localized roughness respectively are also ascertained.Then,the in fl uences of the di ff erent distributions,the geometrical shapes,and the location to the fl at-plate leading-edge of the three-dimensional wall local roughness,and multiple three-dimensional wall local roughness distributed in streamwise and spanwise directions on three-dimensional boundary-layer receptivity are considered.Finally,the e ff ect of the distance between the midpoint of the three-dimensional wall localized roughness and the back-swept angle on three-dimensional boundary-layer receptivity is studied.The intensive research of receptivity in the three-dimensional boundary-layer receptivity will provide the basic theory for awareness and understanding of the laminar-turbulent transition.
receptivity,three-dimensional boundary layer,wall localized roughness
10.7498/aps.66.014703
∗国家自然科学基金(批准号:11472139)、南京信息工程大学人才启动经费(批准号:2016r046)、江苏高校优势学科建设工程和江苏省海洋环境探测工程技术研究中心资助项目.
†通信作者.E-mail:cglu@nuist.edu.cn

