频率对半导体器件热击穿影响的理论模型

张存波 闫涛 杨志强 任伟涛 朱占平

(西北核技术研究所,高功率微波技术重点实验室,西安 710024)(2016年8月19日收到;2016年9月3日收到修改稿)

频率对半导体器件热击穿影响的理论模型

张存波†闫涛 杨志强 任伟涛 朱占平

(西北核技术研究所,高功率微波技术重点实验室,西安 710024)(2016年8月19日收到;2016年9月3日收到修改稿)

针对半导体器件中的热击穿,通过分析已有的理论模型,把频率对器件热区热产生和热传导的影响引入理论模型.利用格林函数求解热传输方程,同时对余误差函数进行近似处理,求解得到热区温度以及器件烧毁功率与频率和脉冲宽度的表达式.通过数值分析,求解得到不同频率下器件烧毁功率随脉冲宽度的变化规律以及不同脉冲宽度下器件烧毁功率随频率的变化规律,同时给出了频率对器件烧毁功率影响的物理解释.

热击穿,频率,脉冲宽度,理论分析

1引 言

热击穿是半导体器件中一种基本的失效机理[1,2].最早分析半导体中热击穿的理论模型由Wunsch和Bell[3]于1968年提出,根据线性热流理论,把恒定功率电脉冲注入下半导体器件内的热效应等效为在无限大介质中半导体结处的一个平面热源产生的热效应,结果表明器件烧毁功率与脉冲宽度的关系为P正比于t−1/2.1970年,Tasca[4]对Wunsch-Bell关系式进行改进,把恒定功率电脉冲注入下半导体器件内的热效应等效为无限大介质中有限大球体为热源的热传输问题,结果表明可以把器件烧毁功率按脉冲宽度分为三个阶段.1983年,Arkihpov等[5]假设热产生区域为长条形圆柱体,推导得到在达到热平衡前的长脉冲情况下器件烧毁功率与脉宽的关系为P正比于1/lnt.1990年,Dwyer等[6]对Wunsch-Bell关系式、Tasca模型以及Arkihpov模型进行对比分析,发现注入功率与脉冲宽度之间的关系表达式强烈依赖于热源的几何结构,并假设热源为矩形平行六面体,求解得到器件烧毁功率按脉冲宽度分为四个阶段,该模型能很好地解释之前的三种模型.

通过对热源几何模型的改进,已有的理论模型能较好地分析器件烧毁功率与脉冲宽度的关系,但理论模型中没有考虑电磁脉冲频率对器件内部热产生及热传导的影响,因而不能分析频率等其他脉冲参数对器件烧毁功率的影响规律.本文通过考虑频率对器件内部热产生及热传导的影响,对已有理论模型进行改进,从而分析频率对器件烧毁功率的影响.

2理论模型

半导体器件内的热效应主要有两个过程,热产生和热传导.已有的物理模型中均假设注入功率恒定,即热产生不与时间、微波频率等其他因素相关,脉冲时间对热传导过程影响显著,从而推导得到了烧毁功率随脉冲宽度的变化分为四个阶段.微波频率与热产生相关性较大,通过分析可知半导体器件内部的电流密度与微波频率相关,热产生与电流密度密切相关.可以通过分析微波频率对电流密度的影响来分析对热产生的影响,并把微波频率对热产生的影响引入理论模型,从而得到器件烧毁功率与微波频率的相关性.

该模型在求解过程中利用了如下简化条件:

1)微波脉冲作用下,器件的热区体积不随微波脉冲的脉宽和频率变化;

2)材料的热导率和比热容为常量,不随温度变化;

3)热区中的热产生是均匀的.

微波脉冲作用下半导体器件中热区(体积Δ)的热产生P(t)=V(t)I(t),热区中的温度分布可以通过求解热传输方程得到,热传输方程如(1)式所示:

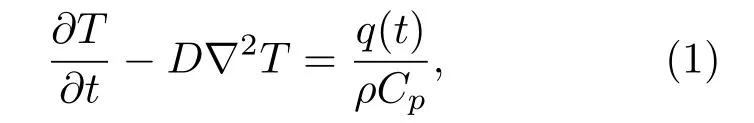
D=K/ρCp为热扩散率,单位m2/s;K为热导率,单位W·m−1·K−1;ρ为密度,单位kg/m3;Cp为比热容,单位J·kg−1·K−1;T 为温度,单位K;q(t)为单位体积的热产生率,在热区中q(t)=P(t)/Δ,不在热区中q(t)为零.这里我们假设热区中的热产生是均匀的.

利用格林函数法,并对时间和空间积分可求得温度分布[6]:

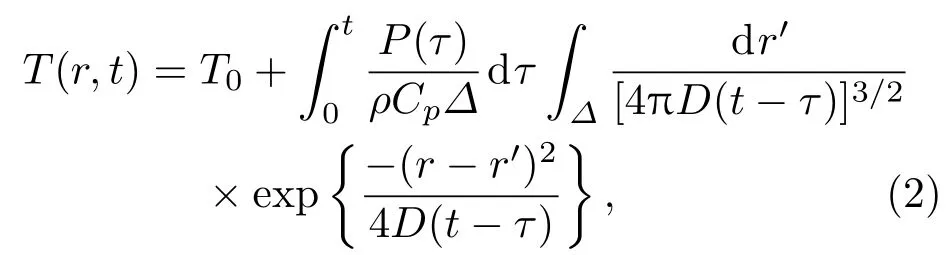
式中T0为环境温度,取值为300 K.假设热区形状为平行六面体,尺寸为a≥b≥c.在笛卡尔坐标系下,积分范围为−a/2≤ x′≤ a/2,−b/2≤y′≤b/2,−c/2≤z′≤ c/2.对空间积分后可求得热区中心处温度与时间的关系式:

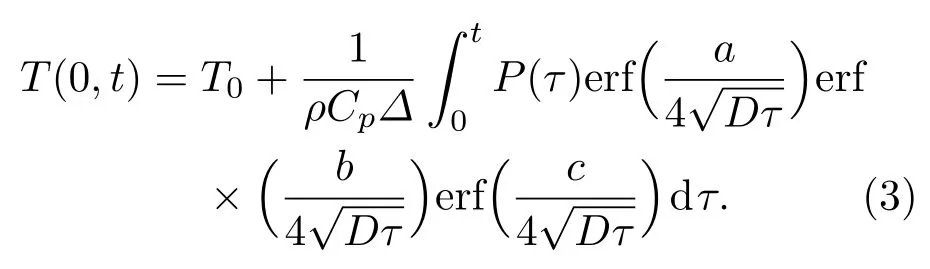
定义与a,b,c相关的热扩散时间ta=a2/4πD,tb=b2/4πD,tc=c2/4πD.ta,tb,tc分别表示为沿x,y,z方向达到热平衡所需要的近似扩散时间,三个扩散时间把时间域分为4个区域.

根据余误差函数的表达式,可以对其进行如下近似

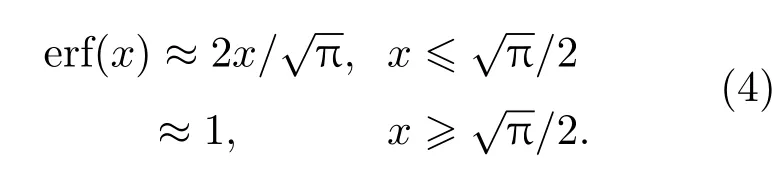
同时可以对表达式(3)中的余误差项进行如下近似

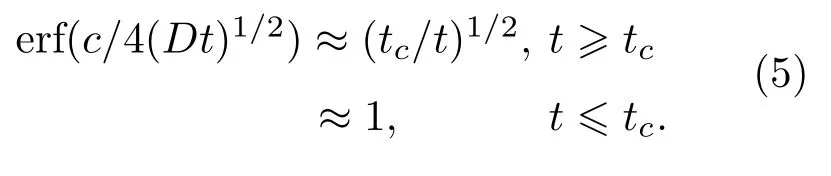
在已有的理论模型中,都是对恒定注入功率进行求解,注入功率与时间及频率无关.为了获得微波脉冲频率对热效应的影响,这里注入功率是时间和频率的函数.注入功率P(t)∝I2(t),微波脉冲作用下半导体器件热区的电流可以表示为I(t)=I0cos(2πft),f为微波脉冲的频率,注入功率也就是热产生可以表示为P(t)=P0cos2(2πft),平均功率P=P0/2.把注入功率的表达式以及表达式(5)代入表达式(3)中进行求解,可以求得热区中心温度与脉冲持续时间以及频率的关系式.热区中心温度的表达式被三个热扩散时间分为四个区域.

区域I:

当≤t≤tc时,求得

区域II:

当tc＜t＜tb时,求得

式中,Pf表示导致器件烧毁所需的平均功率.从热区中心温度以及烧毁功率与脉宽及频率的表达式中无法直接看出两者随频率增加的变化趋势,需要通过数值计算求解得到的变化曲线进行分析.

3数值分析

借鉴文献[6]中GaAs器件的热区尺寸,0.16µm×1.0µm×10.0µm,以及文献[7]中GaAs材料在熔点处的材料参数,如表1所列.计算得到GaAs器件中的热扩散时间分别为tc=0.54ns,tb=21.17ns,ta=2.12µs.利用上面推导得到的公式,可以计算得到不同频率下热区中心温度随时间的变化,以及不同脉宽下烧毁功率随频率的变化,温度达到材料熔点(GaAs熔点1511 K)时判定器件烧毁.

图1给出了P0=0.2 W时,不同频率微波脉冲注入以及恒定功率电脉冲注入下GaAs器件热区中心温度随时间的变化.图中P=P0和P0=P/2曲线表示恒定功率分别为0.2 W和0.1 W的电脉冲注入注入下GaAs器件热区中心温度随时间的变化.红、黑、蓝、紫曲线分别表示P0=0.2 W,微波脉冲频率为f=0.1,1,10,100 MHz时GaAs器件热区中心温度随时间的变化.从图中可知,不同频率微波脉冲注入下,GaAs器件热区中心温度随时间变化与恒定功率电脉冲注入下的变化类似.温度随时间的变化被三个热扩散时间tc,tb,ta分为四个区域.区域I温度增量ΔT=At,区域II温度增量ΔT=Bt1/2,区域III温度增量ΔT=C lnt,区域IV温度增量ΔT→0.频率为f的微波脉冲注入时,温度随时间的变化曲线以2f的频率进行周期性振荡变化,频率越高振荡的幅度越小.随着微波脉冲频率的增加,温度随时间的变化曲线从P=P0曲线向P=P0/2曲线渐变.频率越低曲线越接近P=P0曲线,当频率小于等于10kHz时,曲线与P=P0曲线基本重合;频率越高曲线越接近P=P0/2曲线,当频率大于等于1 GHz时,曲线与P=P0/2曲线基本重合.当频率为10kHz—0.1 GHz时,同一微波脉宽下,频率越高温度增量越小,温度增量随频率的增加而减小.当频率大于1 GHz时,同一脉宽下,温度增量随频率的增加变化非常微小.

表1 材料熔点处的热特性参数Table 1.Thermal parameters of materials at melting point.

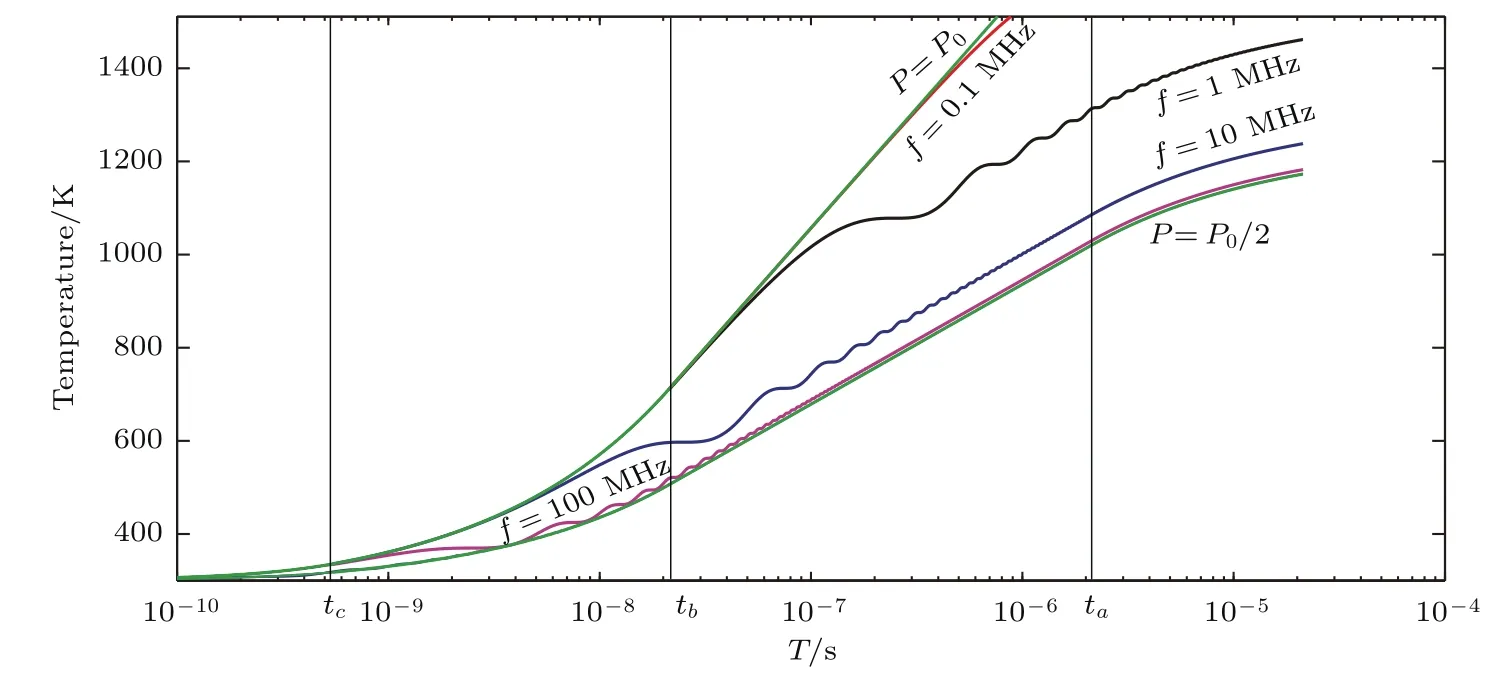
图1 (网刊彩色)GaAs器件热区中心温度随时间的变化Fig.1.(color online)The central temperature in hot zone of GaAs device versus time.

对于热区尺寸a=10.0µm,b=1.0µm,c分别为0.16,0.1,0.05,和0.01µm的GaAs器件,tc＜20ns＜tb,利用区间II中烧毁功率的表达式,得到器件烧毁功率随频率的变化,如图2所示.20ns对应的频率为50 MHz,为了保证不同频率下注入能量相等,20ns应该是各频率下时间周期的整数倍,选取的频率点应该是50 MHz的整数倍.频率范围设置为50 MHz—10 GHz,间隔为50 MHz.烧毁功率随频率增加分为两段,频率小于分段点频率时,烧毁功率随频率增加而增大,频率大于分段点频率时,烧毁功率随频率增加基本恒定但有微小的波动.分段点频率与热区尺寸c相关,c越小分段点频率越高,c为0.01µm时分段点频率大于10 GHz.同一频率下,烧毁功率随热区尺寸c的增大而增大.在a,b尺寸相同的情况下,c越大,热区体积越大,热区温度达到材料熔点所需的能量越多,同一频率下器件烧毁功率越高.

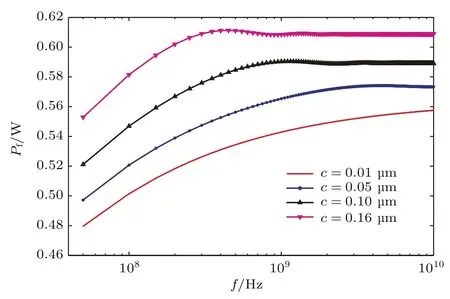
图2 (网刊彩色)脉宽20ns,GaAs器件烧毁功率随频率的变化Fig.2.(color online)Failure power of GaAs device versus frequency at 20ns.

对于热区尺寸a=10.0µm,b=1.0µm,c分别为0.16,0.1,0.05,和0.01µm的GaAs器件,tb＜100ns＜ta,利用区间III中烧毁功率的表达式,得到器件烧毁功率随频率的变化,如图3所示.100ns对应的频率为10 MHz,为了保证不同频率下注入能量相等,100ns应该是各频率下时间周期的整数倍,频率应该是10 MHz的整数倍.频率范围设置为10 MHz—10 GHz,间隔为10 MHz.100ns时烧毁功率随频率增加的变化趋势与20ns时类似.

图3 (网刊彩色)脉宽100ns,GaAs器件烧毁功率随频率的变化Fig.3.(color online)Failure power of GaAs device versus frequency at 100ns.

对于Si器件,上面推导的公式同样适用,表1给出了Si材料的热特性参数[8],通过计算得到Si器件烧毁功率随频率的变化趋势与GaAs器件类似,只是数值上存在差异.文献[9]中利用半导体仿真软件ISE-TCAD仿真得到双极型晶体管烧毁功率随频率的增加而增大,且频率越高,烧毁功率增大的速率越小,与本文理论模型得到的器件烧毁功率随频率的变化趋势类似.

频率对半导体器件烧毁功率影响的物理解释如下:半导体器件热区温度的上升随脉冲宽度的变化分为4个阶段:1)短脉冲下的绝热过程(0≤t≤tc),在该时间尺度下热源产生的热量全部用来使得热源本身的温度上升,没有向外界的传热;2)温度的上升正比于t1/2(tc＜t＜tb),该时间尺度下热源产生的热量通过热区表面向外传导,存在热损耗,该损耗与热区表面积相关;3)温度的上升正比于lnt(tb≤t≤ta),该时间尺度下热区通过表面向外传导的热量更多,但热区的热产生仍然大于热传导,温度上升速率变缓;4)热平衡过程,在该时间尺度下热源产生的热全部通过热区表面向外传导,达到热平衡,热区温度达到稳定不再升高.热区在四个区中的热传导速率随脉宽的增加依次增大,I区中的热传导速率最小,趋于零,IV区中的热传导速率最大,等于热产生的速率.相同注入能量下,在I或II区注入的能量越多,热传导较少,温升就越大.不同频率下,虽然注入总能量相同,但在各个时间区域中注入的能量不相同.频率越低在I或II区注入的能量越多,温升越大,器件更容易烧毁;频率高于一定值时,在各个时间段注入的能量差别很小,器件烧毁功率随频率基本不变.

4结 论

考虑到电磁脉冲作用下半导体器件热区的热产生和热传导受到频率的影响,通过把注入功率设为频率和时间的函数,进而把频率对器件热区热产生和热传导的影响引入理论模型,通过求解热传输方程得到半导体器件烧毁功率与频率的关系.通过数值计算求得器件烧毁功率随频率的增加分为两段,频率小于分段点频率时,烧毁功率随频率的增加而增大,频率大于分段点频率时,烧毁功率随频率的增加基本恒定但有微小的波动.分段点频率与热区最小尺寸c相关,热区尺寸c越小,分段点频率越高.四个时间区域中的热传导速率随脉宽增加依次增大,频率越低在I或II区注入的能量越多,器件更容易烧毁.

[1]Alexander D R 1978 IEEE Trans.Comp.Hybr.and Manufact.Technol.1 345

[2]Khurana B S,Sugano T,Yanai H 1966 IEEE Trans.Electron Dev.ED-13 763

[3]Wunsch D C,Bell R R 1968 IEEE Trans.Nucl.Sci.NS-15 244

[4]Tasca D M 1970 IEEE Trans.Nucl.Sci.NS-17 346

[5]Arkihpov V I,Astvatsaturyan E R,Godovosyn V I,Rudenko A I 1983 Int.J.Electron.55 395

[6]Dwyer V M,Franklin A J,Campbell D S 1989 Solid State Electron.33 553

[7]Franklin A J,Dwyer V M,Campbell D S 1990 Solid-State Electron.33 1055

[8]Choi H H,DeMassa T A 1995 Solid-State Electron.38 939

[9]Ma Z Y,Chai C C,Ren X R,Yang Y T,Chen B,Song K,Zhao Y B 2012 Chin.Phys.B 21 098502

PACS:85.30.De,84.40.–xDOI:10.7498/aps.66.018501

†Corresponding author.E-mail:zhangcunbo@nint.ac.cn

Theoretical model of in fl uence of frequency on thermal breakdown in semiconductor device

Zhang Cun-Bo†Yan Tao Yang Zhi-Qiang Ren Wei-Tao Zhu Zhan-Ping

(Science and Technology on High Power Microwave Laboratory,Northwest Institute of Nuclear Technology,Xi’an 710024,China)(Received 19 August 2016;revised manuscript received 3 September 2016)

In order to analyze the in fl uence of frequency on thermal breakdown in semiconductor device,the in fl uences of frequency on heat generation and heat conduction in the hot zone are introduced into the theoretical model.The heat transfer equation is solved by the Green’s function method,and the error function is approximated.Then,the expressions of temperature in the hot zone and failure power of semiconductor device including frequency and pulse width are derived.The change rules of failure power with the increasing of pulse width under di ff erent frequencies and with the increasing of frequency under di ff erent pulse widths are obtained.The result shows that the expression for center temperature in hot zone caused by the failure power is divided into four time regions,i.e.,regions I-IV,by three thermal di ff usion times ta,tb,and tc.The three di ff usion times ta,tb,and tcare related to the side lengths a,b and c(c≤b≤a)of the hot zone represented by a rectangular parallelepiped,respectively.In region I(0≤t≤tc),the relation between failure power Pfand failure time t is Pf∝ t−1.In this region,the failure time is short and little heat is lost from the surface of hot zone so that the adiabatic term(t−1)dominates.In region II(tc＜ t＜ tb),the relation between failure power Pfand failure time t is Pf∝ t−1/2.In this region,it is indicative of heat loss from the hot zone to its surrounding medium.In region III(tb≤t≤ta),the relation between failure power Pfand failure time t is Pf∝1/lnt.In region IV(t＞ta),the failure power Pfis constant.In this region,the failure time is very large and thermal equilibrium can be established so that the steady state term dominates.The relation between failure power and frequency is divided into two parts.In part one,the failure power increases with the increasing of frequency;in part two,the failure power is nearly constant with the increasing of frequency.Meanwhile,the physical interpretation of the in fl uence of frequency on failure power is given.From region I to region IV,each heat transfer rate increases with pulse width.The lower the frequency,the more the injection energy during region I or region II is,when the total injection energy is constant.The heat transfer rate is slower in region I or region II,so the energy converted into heat will be more and the temperature in the hot zone will be higher,thus the device is burned out easily.

thermal breakdown,frequency,pulse width,theoretical analysis

10.7498/aps.66.018501

†通信作者.E-mail:zhangcunbo@nint.ac.cn