定向退火条件下柱状晶形成及连续扩展的相场模拟
罗志荣 ,高英俊, ,邓芊芊,黄礼琳 ,黄创高,
(1. 玉林师范学院 物理科学与工程技术学院,玉林 537000;2. 广西大学 物理科学与工程技术学院,南宁 530004;3. 广西大学 广西有色金属及特色材料加工重点实验室,南宁 530004)
材料的力学、热学和电学等性能强烈地依赖于其微观结构。因此,为了设计生产满足不同性能需求的材料,更深入地研究材料微观结构演化机理显得尤为重要[1-3]。多晶体材料的晶粒尺寸及其均匀性是影响材料性能的关键因素,采用热处理工艺来控制晶粒长大是提高材料性能的常用方法[4]。高温材料要求具有较粗大的晶粒才能使得材料具有足够的高温强度和抗蠕变能力。通过控制晶界结构,实现晶粒组织定向化是改善和提高高温材料性能的有效手段[5]。其中,定向退火已经在实验上成功应用于高温材料产生柱状晶结构[6-7]。柱状晶具有优良的抗蠕变性能[8]和抗疲劳能力[9]以及抑制裂纹扩展[5,10]等优点,因此,研究定向退火条件下柱状晶的形成过程具有重要的实际意义。
近年来,已有学者采用计算机模拟方法研究了定向退火条件下的晶粒长大过程,其中以蒙特卡罗法(Monte Carlo method)、前端追踪法(Front-tracking method)和相场法(Phase field method)为主。HOLM等[11]采用蒙特卡罗法模拟了局部退火时非均匀晶粒长大行为,并分析了晶粒长大动力学。BADMOS等[12-13]采用前端追踪法研究了单相材料中柱状晶的长大过程及晶界能和晶界迁移率各向异性对柱状晶长大的影响,值得注意的是,其研究结果表明柱状晶长大没有最小热区移动速率临界值。魏承炀等[14]通过设定晶界迁移率为高斯函数,采用相场法研究多晶材料在定向退火过程中由温度梯度引起的非均匀晶粒长大和定向晶粒长大行为。
在众多研究材料微观结构的计算方法中,相场法因具有深刻的物理思想,不需要追踪复杂界面的运动等优势而成为强有力的计算方法[15],已经广泛应用于研究晶粒长大[16]、再结晶[17-18]和凝固[19-20]等现象。在前期的研究工作中,本文作者[21]构建了定向退火条件下的移动热区模型(该模型在模拟定向退火时具有简单且实用的优点),并研究了热区温度等因素对柱状晶形成的影响。在文献[21]的研究基础上,本文作者采用相场法研究定向退火条件下移动热区宽度对柱状晶形成及连续扩展的影响,探究柱状晶形成和连续扩展的规律。
1 模型与方法
1.1 相场模型
在单相多晶材料晶粒演化的相场模型中,采用一系列非保守的取向场变量η1(r,t),η2(r,t),…,ηP( r,t )描述晶粒在空间位置r的不同取向,其中P为晶粒取向个数。体系总自由能泛函F可以表示为[22]
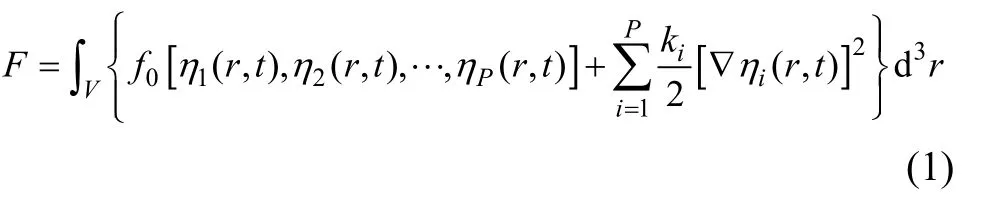
式中:f0为自由能密度函数;ki为能量梯度系数。为了能够描述多晶材料微观组织,对f0的基本要求是:存在 2P个大小相等的简并极小值,且极小值位于(η1, η2,⋅⋅⋅,ηP) = (1,0,⋅⋅⋅,0),(0,1,⋅⋅⋅,0),⋅⋅⋅,(0,0,⋅⋅⋅,1),(-1,0,⋅⋅⋅,0),(0,-1 ,⋅⋅⋅,0 ),⋅⋅⋅,(0 , 0,⋅⋅⋅,-1 ),从而保证空间中每个位置只有一个取向,且每个取向在空间位置的概率相等。满足上述要求的f0可以构建为[22]
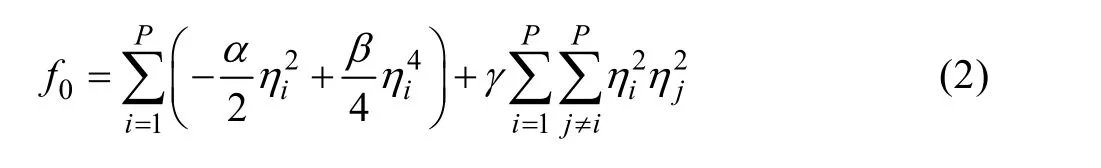
式中:α、β和γ为唯象参数,要求γ>β/2。
由于取向场变量是非保守场变量,它们随时间的演化由Ginzburg-Landau方程组描述[22]
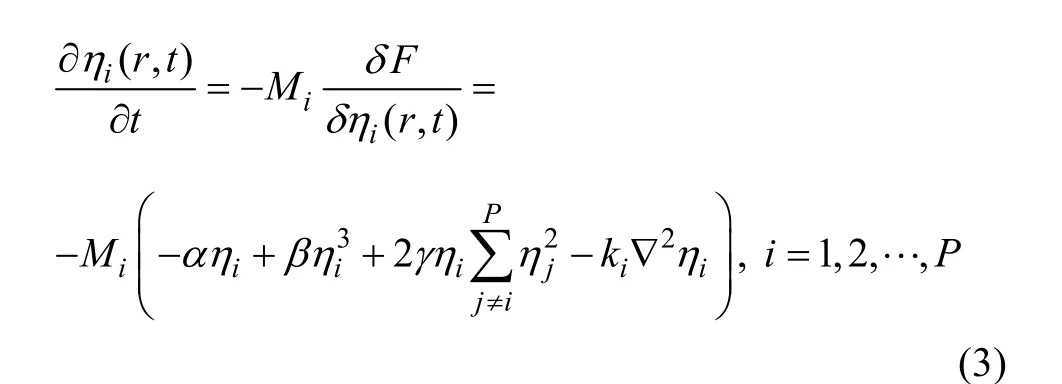
式中:M为晶界迁移率;t为时间。
1.2 数值化处理
为了数值求解动力学方程组(式(3)),需要将它们在时间和空间上进行离散化处理。在时间上采用显式Euler迭代公式[22]:

式中:Δt为时间步长。在空间上将Laplace算子采用九点差分格式离散[23]:
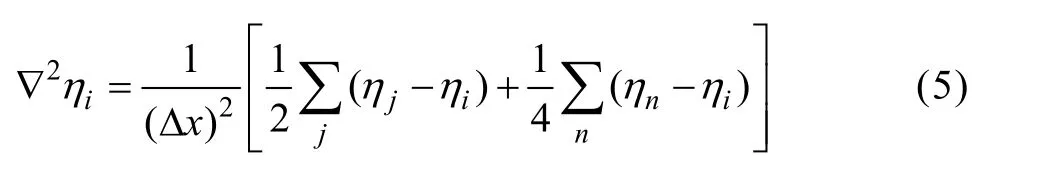
式中:Δx为空间步长;j和n分别代表i的最近邻格点与次近邻格点。
1.3 晶界迁移率的设置
在退火过程中,温度通过晶界迁移率对晶粒长大过程产生直接影响,而不均匀温度场影响晶粒长大的本质是与之有关的不均匀晶界迁移率对晶粒长大的影响[14]。在定向退火过程中,温度梯度通常由晶界迁移率梯度来体现[11]。选取具有无限大温度梯度的热区,且热区以速率v做匀速运动,如图1所示。在热区内温度均匀,且晶粒长大只发生在热区内,热区外晶粒不长大。式(3)中晶界迁移率M设定为[21]

式中:Mh为热区内晶界迁移率。
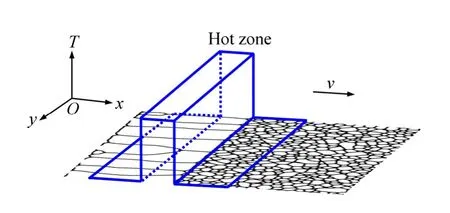
图1 具有无限大温度梯度的移动热区示意图[21]Fig. 1 Schematic diagram of moving hot zone with infinite temperature (T) gradient[21]
1.4 参数选取
本研究不涉及具体材料的物性参数,所采用的参数均已无量纲化。计算时将连续空间离散为四方格子,采用周期性边界条件。计算区域为512×512 gp(gp表示格子点数),P=36,α=1.0,β=1.0,γ=1.0,Mh=1.0,空间步长Δx=2.0 gp,时间步长Δt=0.25 ts。
通过设定晶界迁移率为常数来模拟在温度场均匀分布情况下体系晶粒长大500 ts后得到的微观组织,将其作为初始组织(平均晶粒直径D=14.1 gp),如图2所示。随后对体系进行定向退火,定向退火时热区从体系最左端向右(见图1中x轴正方向)匀速移动。图中灰色区域表示热区位置。

图2 初始细小等轴晶Fig. 2 Initial fine equiaxed grain
2 模拟结果与分析
2.1 热区宽度对柱状晶形成的影响
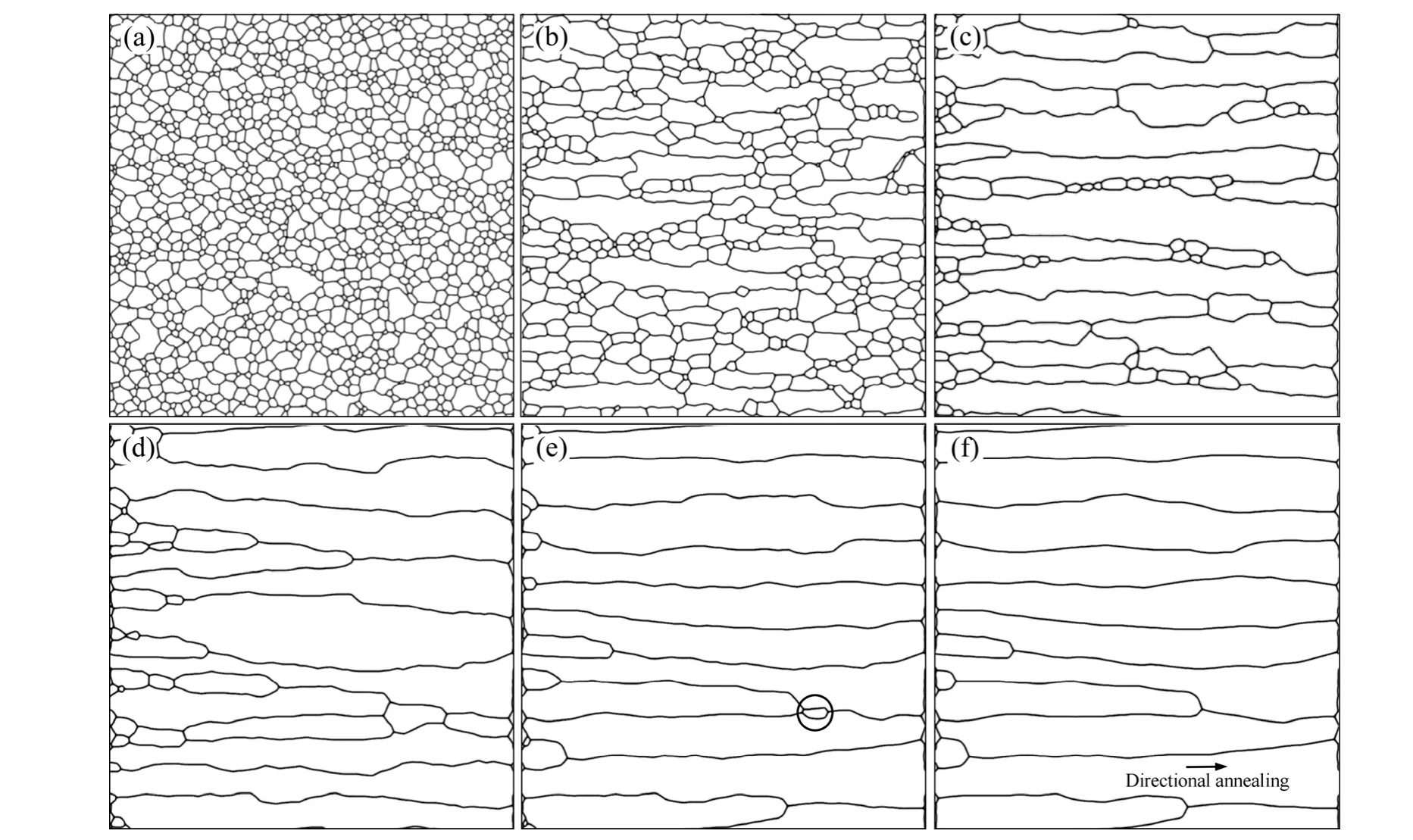
图3 体系在不同宽度的热区作用下以移动速率v=0.002 gp/ts定向退火所获得晶粒的形貌Fig. 3 Grain morphologies of system at same hot zone speed (v=0.002 gp/ts) and different hot zone widths W during directional annealing : (a) W=5 gp; (b) W=10 gp; (c) W=15 gp; (d) W=20 gp; (e) W=30 gp; (f) W=50 gp
图3所示为体系在不同热区宽度下以相同移动速率(v=0.002 gp/ts,即每模拟500 ts,热区移动1 gp)从体系最左端移动至最右端后得到的晶粒形貌。由图 3可见,当热区宽度很小(W=5 gp)时,所得晶粒相对于初始晶粒(见图2)只是整体粗化,但仍保持等轴晶结构(见图3(a))。当热区宽度增加到10 gp时,所得晶粒沿热区移动方向被拉长,并且存在一部分较粗大的长条晶粒(见图3(b))。当热区宽度达到15 gp时,得到柱状晶与等轴晶并存的混合晶粒结构(见图3(c))。当热区宽度达到20 gp时,大部分晶粒为柱状晶,但仍存在少部分等轴晶(见图 3(d))。随着热区宽度的增加,所得晶粒中等轴晶逐渐减少。当热区宽度增大到30 gp时,所得晶粒结构除了图 3(e)中圆形区域外,其余为柱状晶。当热区宽度增大至50 gp时,得到平直的柱状晶结构(见图3(f))。这是因为热区宽度较大时,热区内晶粒长大及长大前端的形成时间较长,从而在柱状晶间形成平行于热区移动方向的平直晶界。
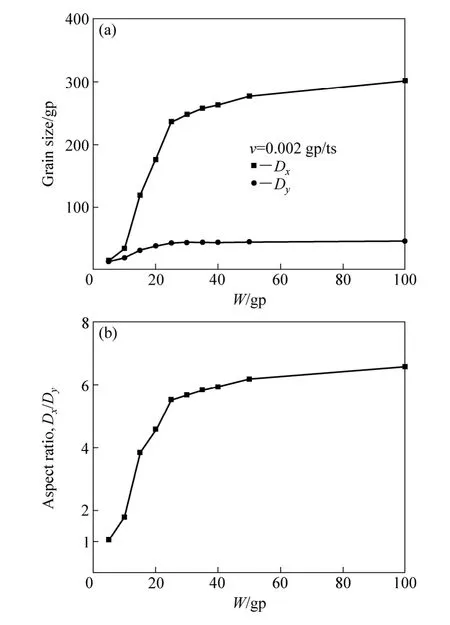
图4 晶粒尺寸和晶粒长宽比与热区宽度W的关系Fig. 4 Relationship between grain size (a) and aspect ratio (b)and hot zone width
对于柱状晶结构,晶粒尺寸用晶粒长度和晶粒宽度表示。在热区移动速率保持不变、热区宽度(W)不同的条件下,定向退火后所得晶粒的尺寸(晶粒长度Dx和晶粒宽度Dy)及其长宽比Dx/Dy与热区宽度W的关系曲线分别见图4(a)和(b)。由图4可见,在W不超过5 gp时,晶粒的长宽比Dx/Dy约为1,晶粒为等轴晶结构。当W达到15 gp时,Dx就快速增加到Dy的4倍左右,形成了较明显的柱状晶结构。当W继续增大时,所得晶粒的长宽比Dx/Dy仍继续增大,但增大幅度趋于平缓。这是因为在热区宽度较小时,热区内晶粒长大时间较短,所以所得晶粒大部分为等轴晶;而在热区宽度较大时,热区内晶粒长大时间较长,晶粒不断长大,且随着热区的移动,晶粒在垂直于热区移动方向由于晶粒的相互碰撞而受到抑制,所以得到晶界较平直的柱状晶结构。可见,在热区移动速率一定时,增加热区宽度有利于形成柱状晶结构,且所得柱状晶的长宽比随着热区宽度的增加而增大。
2.2 热区宽度对柱状晶连续扩展的影响
为了研究热区宽度对柱状晶连续扩展的影响,首先在一个较大热区宽度(W=30 gp)下以速率v=0.002 gp/ts进行定向退火,形成一段柱状晶结构(见图 5(a)中灰色区域左侧的晶粒组织);然后将热区宽度减小到某一个值,再以原热区移动速率(v=0.002 gp/ts)沿原热区运动方向继续定向退火。当热区宽度W=15 gp时,所获得的晶粒结构如图5(b)所示。对比图5(b)和图3(c)可见,虽然两者的热区宽度相同(W=15 gp),但在初始等轴晶基础上,定向退火所获得的晶粒结构为柱状晶和等轴晶并存的混合结构(见图 3(c)) ;而在有一段柱状晶(见图5(a))基础上减小热区宽度后继续定向退火,柱状晶仍能连续扩展,即得到的晶粒形貌仍然保持柱状晶结构(除图 5(b)中圆形区域外)。可见,当热区移动速率保持恒定时,柱状晶连续扩展比柱状晶形成所需临界热区宽度要小。
当热区宽度W=10 gp时,柱状晶在扩展过程中被破坏,所得晶界结构为柱状晶与等轴晶混合的晶粒结构(见图5(c))。这是因为在热区移动速率恒定时,若热区宽度太小(见图5(c)),当三叉晶界处的脊超过热区宽度时,只有一部分三叉晶界处在热区内部作为晶粒生长前端而扩展,导致柱状晶连续扩展失败。柱状晶结构的连续扩展需要在热力学上处于劣势的晶粒被其他晶粒吞噬,且晶粒长大前端能够随着热区一起移动,这需要柱状晶在热区内停留一定时间,当热区移动速率恒定时,就要求热区宽度不能太小。
从图5(c)还可以观察到,宽度较小的柱状晶(晶粒A)在连续扩展过程中被破坏;而宽度较大的柱状晶(晶粒B)在连续扩展过程中一直保持柱状晶结构。可见,较粗大的柱状晶在连续扩展过程中更易保持柱状晶结构。这是因为柱状晶连续扩展与晶界迁移速率有关,
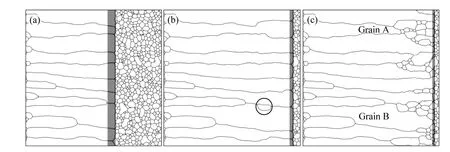
图5 热区宽度对柱状晶连续扩展的影响(热区移动速率v=0.002 gp/ts)Fig. 5 Effect of hot zone width W on continuous propagation of columnar grain structure (hot zone speed v=0.002 gp/ts) (Position and width of hot zone are indicated by gray rectangular regions): (a) W=30 gp; (b) W=15 gp; (c) W=10 gp
而在热区内柱状晶与初始等轴晶之间的晶界中,三叉晶界的迁移速率最小。热区内较粗大的柱状晶与初始等轴晶之间的晶界段的曲率较小,对应的晶界驱动力更大,所以较粗大的柱状晶更易连续扩展。
2.3 柱状晶连续扩展的热区移动临界速率
以图 5(a)中晶粒组织为模拟初态,分别在不同热区宽度(15~60gp)和热区移动速率(0.00067~0.0054 gp/ts)的条件下继续对样品进行定向退火。图6所示为定向退火时柱状晶连续扩展的热区移动临界速率与热区宽度的关系曲线。图 7(a)~(f)所示分别为图 6中点A~F所对应的晶粒组织。柱状晶的形成和连续扩展实质上都是柱状晶的前端晶粒不断地向初始细小等轴晶粒迁移的过程。由图7可见,在热区宽度一定时,当热区移动速率等于或小于临界速率时柱状晶才能连续扩展(见图 7(a)~(c));当热区移动速率超过临界速率时,柱状晶在扩展过程中会发生断裂,形成柱状晶与等轴晶都存在的混合结构(见图7(d)~(f))。

图 6 柱状晶连续扩展的热区移动临界速率与热区宽度的关系Fig. 6 Relationship between critical speed for continuous propagation of columnar structure and hot zone width
根据热区宽度的不同,图6中柱状晶连续扩展的热区移动临界速率与热区宽度的曲线分成两个阶段,在热区宽度较小(W<1.5D)和热区宽度较大(W>1.5D)时分别有不同的变化规律。当热区宽度较小时,随着热区宽度的增加,临界速率快速增加;当热区宽度达到阈值(1.5D)后,随着热区宽度的增加,临界速率的增加趋缓。说明热区宽度对临界速率的影响存在一个阈值,超过阈值,临界速率对热区宽度变化不敏感。
3 结论
1) 当热区移动速率保持恒定时,增加热区宽度有利于形成柱状晶结构,且所得柱状晶的长宽比随着热区宽度的增加而增大。
2) 柱状晶连续扩展所需临界热区宽度小于形成柱状晶所需临界热区宽度,在连续扩展过程中,较粗大的柱状晶更易保持柱状晶结构。
3) 热区宽度对柱状晶连续扩展的热区移动临界速率的影响存在一个阈值。当热区宽度小于初始晶粒直径的1.5倍时,热区移动临界速率随着热区宽度的增加而显著增加;当热区宽度大于初始晶粒直径的1.5倍时,热区移动临界速率随着热区宽度的增加而缓慢增加,热区宽度的影响减弱。
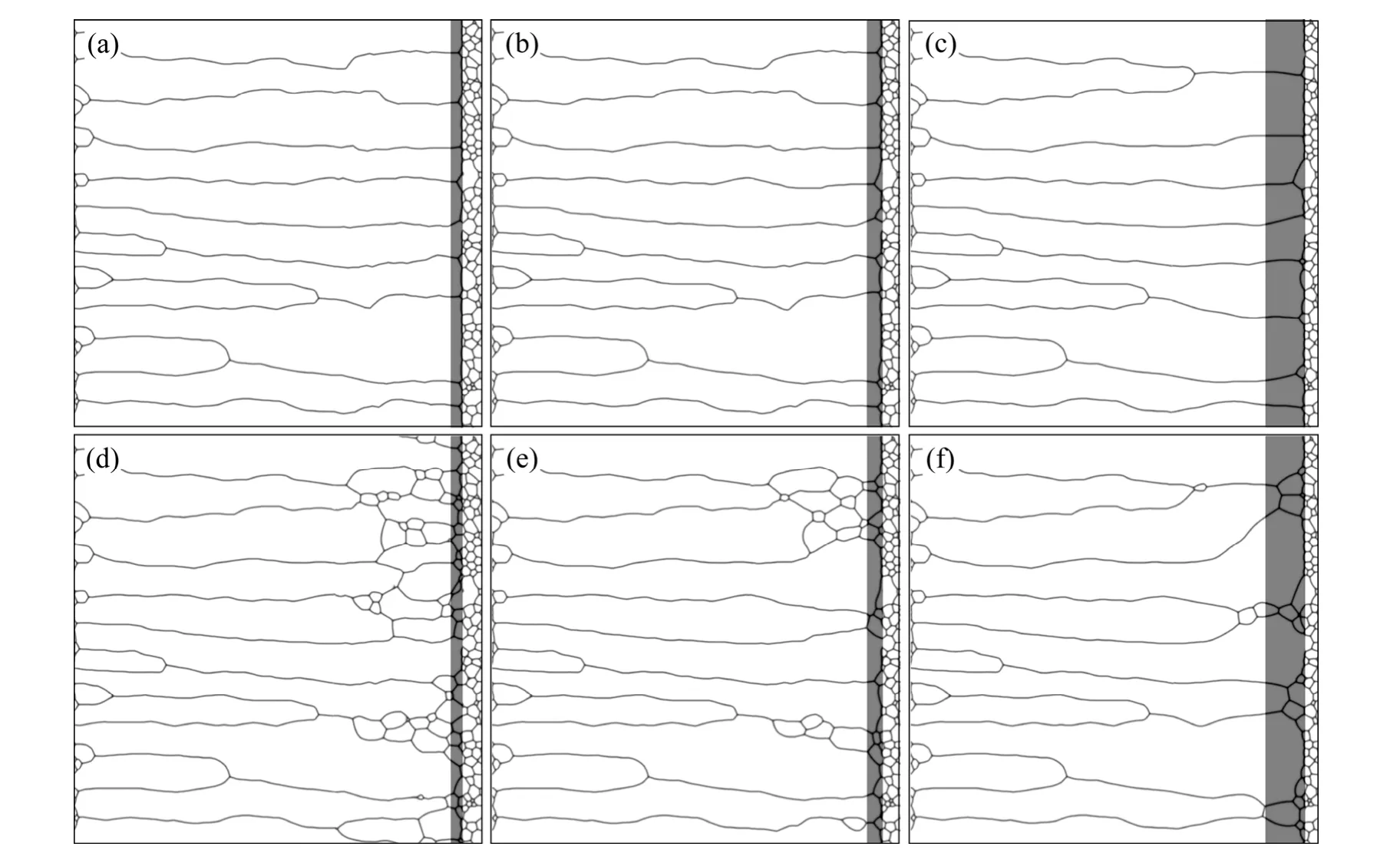
图7 不同热区宽度和移动速率下得到的晶粒形貌(图7(a)~(f)分别对应图6中点A~F)Fig. 7 Grain morphologies of different hot zone widths and speeds (Fig.7(a)~(f) corresponding to points from A to F in Fig. 6,respectively): (a) W=15 gp, v=0.00067 gp/ts; (b) W=20 gp, v=0.0033 gp/ts; (c) W=50 gp, v=0.0044 gp/ts; (d) W=15 gp, v=0.0050 gp/ts; (e) W=20 gp, v=0.0050 gp/ts; (f) W=50 gp, v=0.0054 gp/ts
[1] HOSFORD W F. Mechanical behavior of materials[M].Cambridge: Cambridge University Press, 2005.
[2] RHINES F N. Microstructure-property relationships in materials[J]. Metallurgical Transactions A, 1977, 8(1): 127-133.
[3] LI J C M. Microstructure and properties of materials[M].Singapore: World Scientific, 2000.
[4] HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena[M]. 2nd ed. Oxford: Elsevier Science, 2004.
[5] ZHANG Z W, CHEN G L, CHEN G. Microstructural evolution of commercial pure iron during directional annealing[J].Materials Science and Engineering A, 2006, 422(1/2): 241-251.
[6] BAKER I, LI J. Directional annealing of cold-rolled copper single crystals[J]. Acta Materialia, 2002, 50(4): 805-813.
[7] ZHANG Z W, CHEN G, CHEN G L. Dynamics and mechanism of columnar grain growth of pure iron under directional annealing[J]. Acta Materialia, 2007, 55(17): 5988-5998.
[8] BEDDOES J, SEO D Y, SAARI H. Long term creep of TiAl+W+Si with polycrystalline and columnar grain[J]. Scripta Materialia, 2005, 52(8): 745-750.
[9] GODFREY A W, MARTIN J W. The effect of directional recrystallization on the low cycle fatigue response of a powder metallurgy nickel-based superalloy at elevated temperatures[J].Materials Science and Engineering A, 1997, 222(2): 91-100.
[10] CAIRNS R L, CURWICK L R, BENJAMIN J S. Grain growth in dispersion strengthened superalloys by moving zone heat treatments[J]. Metallurgical Transactions A, 1975, 6(1):179-188.
[11] HOLM E A, ZACHAROPOULOS N, SROLOVITZ D J.Nonuniform and directional grain growth caused by grain boundary mobility variations[J]. Acta Materialia, 1998, 46(3):953-964.
[12] BADMOS A Y, FROST H J, BAKER I. Microstructural evolution during directional annealing[J]. Acta Materialia, 2002,50(13): 3347-3359.
[13] BADMOS A Y, FROST H J, BAKER I. Simulation of microstructural evolution during directional annealing with variable boundary energy and mobility[J]. Acta Materialia, 2003,51(10): 2755-2764.
[14] 魏承炀, 李赛毅. 温度梯度对晶粒生长行为影响的相场模拟[J]. 物理学报, 2011, 60(10): 100701-1-8.WEI Cheng-yang, LI Sai-yi. Effect of temperature gradient on grain growth behavior from phase field simulations[J]. Acta Physica Sinica, 2011, 60(10): 100701-1-8.
[15] CHEN L Q. Phase-field models for microstructure evolution[J].Annual Review of Materials Research, 2002, 32(1): 113-140.
[16] FAN D, CHEN L Q. Computer simulation of grain growth using a continuum field model[J]. Acta Materialia, 1997, 45(2):611-622.
[17] 高英俊, 罗志荣, 胡项英, 黄创高. 相场方法模拟AZ31 镁合金的静态再结晶过程[J]. 金属学报, 2010, 46(10): 1161-1172.GAO Ying-jun, LUO Zhi-rong, HU Xiang-ying, HUANG Chuang-gao. Phase field simulation of static recrystallization for AZ31 Mg allloy[J]. Acta Metallurgica Sinica, 2010, 46(10):1161-1172.
[18] 罗志荣, 高英俊, 朱甜霞, 卢强华, 林 葵. 相场方法研究变形镁合金的晶粒分布[J]. 中国有色金属学报, 2013, 23(6):1496-1506.LUO Zhi-rong, GAO Ying-jun, ZHU Tian-xia, LU Qiang-hua,LIN Kui. Phase field model for grain distribution of deformation magnesium alloy[J]. The Chinese Journal of Nonferrous Metals,2013, 23(6): 1496-1506.
[19] 袁训锋, 丁雨田. 强界面能各向异性下二元 Ni-Cu合金枝晶生长过程的相场法模拟[J]. 中国有色金属学报, 2011, 21(7):1656-1663.YUAN Xun-feng, DING Yu-tian. Phase-field simulation of dendrite growth process for binary Ni-Cu alloy with anisotropy of strong interface energy[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(7): 1656-1663.
[20] ZHANG Shu-zhou, ZHANG Rui-jie, QU Xuan-hui, FANG Wei,LIU Ming-zhi. Phase field simulation for non-isothermal solidification of multicomponent alloys coupled with thermodynamics database[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(8): 2361-2367.
[21] 罗志荣, 刘 瑶, 邓芊芊, 黄礼琳, 高英俊. 相场方法研究定向退火条件下柱状晶粒的形成过程[J]. 广西物理, 2013, 34(1):9-13.LUO Zhi-rong, LIU Yao, DENG Qian-qian, HUANG Li-lin,GAO Ying-jun. Phase field study of the formation of columnar-grain structure during directional annealing[J].Guangxi Physics, 2013, 34(1): 9-13.
[22] CHEN L Q, YANG W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: The grain-growth kinetics[J].Physical Review B, 1994, 50(21): 15752-15756.
[23] OONO Y, PURI S. Computationally efficient modeling of ordering of quenched phases[J]. Physical Review Letters, 1987,58(8): 836-839.
——《热区特色农业产业发展与关键技术专刊》刊首语

