基于方向A*算法的温室机器人实时路径规划

张 文 刘 勇 张超凡 张 龙 夏营威

(1．中国科学院合肥物质科学研究院应用技术研究所，合肥230031;2．中国科学技术大学，合肥230026)

基于方向A*算法的温室机器人实时路径规划

张 文1，2刘 勇1张超凡1，2张 龙1夏营威1

(1．中国科学院合肥物质科学研究院应用技术研究所，合肥230031;2．中国科学技术大学，合肥230026)

针对复杂环境下的温室机器人路径规划问题，重点研究了生成路径的平滑设计、碰撞检测和算法实时性，提出一种方向A*算法。首先采用“视野线”平滑原则优化路径，消除锯齿效应并避免部分碰撞;其次应用“圆弧—直线—圆弧”转弯策略，避免机器人本体宽度影响;最后基于二叉堆加速算法，提升算法计算效率。仿真实验结果表明，方向A*算法满足平滑要求且能有效避免碰撞，加速算法平均提速4～7倍。同时，机器人在真实实验环境下能实现安全自主导航，跟踪误差小于0.15m，验证了所提方法的可行性。

温室机器人;路径规划;方向A*算法;二叉堆

引言

路径规划是温室机器人实现自主导航的核心问题，指在具有障碍物的环境下，按照一定的评价标准，搜索一条从起始状态(位置和姿态)到目标状态的最优或次优的安全无碰撞路径［1－3］。根据环境感知信息的不同程度，目前路径规划方法主要分为两类:一是基于已知环境信息的全局路径规划方法(人工势场法［4］、栅格法［5］、A*算法);二是基于实时传感器数据的局部路径规划方法(D*算法［6］、遗传算法［7］、蚁群算法［8］)。

A*算法是一种基于启发式函数的全局路径规划方法，适用于二次规划［9］。但传统A*算法忽略了动态环境变化和机器人本体信息，易舍弃部分点而生成次优结果，造成拐点多、路径长，不利于运动控制及路径跟踪［10］。BOISSONNAT等［11］最早采用直线—圆弧平滑算法消除跳变，路径在一定程度上得到平滑。TROCATO等［12］利用微分改进A*算法，大大减少转折次数，然而由于涉及大量数学计算及推导，未能兼顾算法实时性。王殿君［13］基于栅格编码信息，动态获取旋转方向及角度，但未考虑未知障碍物信息和机器人本体宽度。

本文在分析传统A*算法的基础上，重点研究生成路径的平滑设计、碰撞检测和算法实时性，提出一种方向A*算法，并应用于中国科学院贝贝机器人本体，旨在实现复杂温室环境下的自主导航功能。

1 基于方向A*算法的路径规划

本文提出的方向A*算法主要涉及A*算法的后处理方法，首先对生成路径进行“视野线”平滑，在消除锯齿效应的同时兼顾碰撞问题;其次应用“圆弧—直线—圆弧”转弯策略，避免机器人本体宽度影响;最后基于二叉堆提高数据交互效率，以满足机器人实时计算要求。

1.1 传统A*算法分析

传统A*算法结合BFS算法和Dijkstra算法的优点，通过定义估价函数来评估代价而确定最优路径。估价函数为

式中 n——待扩展的节点

g(n)——起始点到当前节点的实际代价值

h(n)——当前点到目标点的估计代价值，即启发函数

f(n)——从起始点经过节点n到达目标点的最优代价解的估计代价［14－15］

A*算法的基本思想是通过设置合适的启发函数，全面评估各扩展搜索节点的代价值，通过比较各扩展节点的代价值，选取代价最小节点加以扩展，直至到达目标点。针对栅格化环境地图的路径搜索，一般选用曼哈顿距离或欧几里得距离作为启发函数［16］。

1.2 “视野线”平滑准则

由于传统A*算法依据8邻域搜索节点，必然会产生锯齿效应，造成路径折线长、拐点多(图1a)。常规平滑算法常在转弯时采取惩罚机制，会减少部分拐点(图1b)，但依然会存在45°斜坡，欠平滑且导航耗时。

图1 不同方法下的锯齿效果对比图Fig．1 Contrast of zigzag images after differentmethods

为获取图1c中的最优路径，提出一种“视野线”平滑算法:对当前节点，视野范围所能到达的最远节点直接连通并舍弃中间节点，依此继续分析直至扫描路径结束。具体实施步骤如下:

(1)传统A*算法处理后，沿生成路径依次分析各节点。

(2)路径起始点为startpos，startpos－＞next为currentpos。

(3)如果currentpos的子节点存在，则继续，否则跳至步骤(7)。

(4)GoThrough(startpos，currentpos－＞next)得返回值，若为真值则继续，否则跳至步骤(6)。

(5)将currentpos赋值为currentpos－＞next并删除currentpos之前指向的节点，跳至步骤(3)。

(6)startpos赋值为 currentpos，currentpos赋值为currentpos－＞next，跳至步骤(3)。

(7)路径平滑结束。

其中，函数GoThrough(posA，posB)在posA和posB之间按照固定间隔(通常1/5栅格长度)采样，依次检查各样本点:机器人以当前点为质心，1/2机器人宽为探索范围，判断其4邻域是否碰撞障碍栅格，若没有则返回真值，反之为假。根据“视野线”平滑路径后，图1a中多余的红圈拐点予以消除，得到图1c所示路径。

1.3 “圆弧—直线—圆弧”转弯策略

1.3.1 增加合理的转弯

“视野线”平滑准则固然能优化路径，但当机器人本体过大或遭遇拐点栅格时，往往无法通过。因此，本文将引入合理的转弯方法，避免突然变向和碰撞，这种思想最早用于处理游戏地图中的人工智能问题。

首先，应理解转弯半径概念。假如机器人向右后行驶时，一般主动轮会先向右或向左旋转到限制位，行进时将产生一段圆弧，此圆的半径即转弯半径。倘若机器人处于图2的某起始点(Origin)并具有方向，需前行至目标点(Destination)，最短路径有且仅有2种(图2绿线部分):按转弯半径右转，直到“视野线”看到目标点，然后继续前进;同理得左转方式。

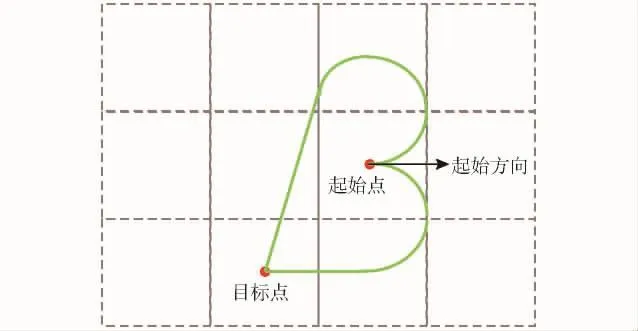
图2 两种最短路径规划图Fig．2 Planning image of two shortest paths

图3 右转路径长度计算示意图Fig．3 Schematic diagram of calculating length of right turn path

为计算路径长度，将右转路线表示为图3，并根据几何关系说明。图3中，r为转弯半径，P为转弯时的圆心。若起始点按图示方向右转，P的方向和位置为

式中 dP——P相对于起始点的方向角

dO——起始点的方向角

xP、yP——点P的横坐标和纵坐标

xO、yO——起始点的横坐标和纵坐标

然后计算点P到目标点的距离

式中 dx——点P和目标点横坐标之间的差值

dy——点P和目标点纵坐标之间的差值

xD、yD——起始点的横坐标和纵坐标

l——点P和目标点的距离

判断l与半径r的大小，若l小于半径r，则目标点在圆内，永远无法到达。Q为离开圆弧开始直线距离的点，根据三角关系，可以获取Q到目标点的距离及l和r的夹角

式中 d——Q到目标点的距离

θ——l与r的夹角

最后，计算点Q的方向和位置

xQ、yQ——点Q的横坐标和纵坐标

同理，左转路线可依此计算，但有2处区别:一是P的方向加上90°，二是计算点Q坐标时，用θ－取代。计算完成后，比较2种转弯方式路径长度，短的路径即最终选取路径。

1.3.2 “圆弧—直线—圆弧”策略

应用方向A*算法规划最短路径时，仅已知起始点方向、位置和转弯半径显然不足，为防止碰撞及获取下次起始点的方向，还需考虑到达目标点时的方向。因此，扩展上述转弯方法，提出一种“圆弧—直线—圆弧”转弯策略。

增加确定的到达方向后，出现图4中4种可能的路径方式。可以看出，到达目标点时，也有类似出发点一样的圆弧来保证方向的正确性。此时，各路径方案中都有固定的3段:第1段圆弧、中间直线段和第2段圆弧，故为“圆弧—直线—圆弧”策略。

图4 具有固定方向的4种转弯路径Fig．4 Four turning pathswith a fixed direction

对于图4的情况，采取类似图3同样的计算方法能够较易得到起始点和目标点的位置，但关键是如何获取离开第1段圆弧和到达第2段圆弧时各点的方位和角度。一般，需考虑两种情况。第1种是离开起始点和到达目标点转弯时，绕圆心旋转在同一方向，例如图5中都是顺时针方向。此时，P1到P2的蓝色连线与其正下方的绿线具有相同的长度和斜率，可以得到

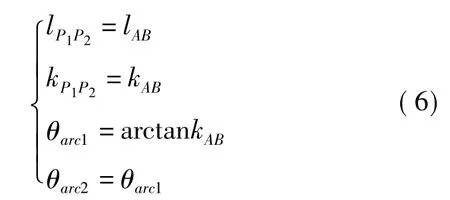
式中 lP1P2——点P1到P2的距离

lAB——点A到点B的距离

kP1P2——直线P1P2的斜率

kAB——直线AB的斜率

θarc1——离开第1段圆弧时的角度

θarc2——到达第2段圆弧时的角度

图5 路径搜索时以相同方向转弯示意图Fig．5 Traveling around both circles in the same direction

第2种是离开起始点和到达目标点转弯时，方向是相对的，例如图6中离开是顺时针方向，到达是逆时针方向。为简化计算，相对目标圆作相同圆(圆心P3)与其正切于点B，此时第3圆与起始圆的关系就演变成第1种情况。在△P1P2P3中，可得

式中 lP2P3——点P2到P3的距离

θ1——P2P3与P2P1的夹角

图6 路径搜索时以相对方向转弯示意图Fig．6 Traveling around both circles in opposite direction

θAB——直线AB与x坐标轴夹角至此，可以获取离开第1段弧和到达第2段弧的角度。

综上所述，对于已知位置和方向的起始点和目标点，能够实时计算4种可能路径来获取最短路径，并避免机器人本体宽度造成的碰撞。同时，可以获取当前路径中任意时刻的位置和方向。

1.4 方向A*平滑算法

为平滑路径、避免碰撞，本文在上述基础上扩展为更为复杂的方向A*算法。首先，在传统的二维栅格地图基础上增加方向维度，使得地图中的各节点具有潜在的8个罗盘方向(N、S、E、W、NE、NW、SE、SW)，例如某节点可表示为［X=45，Y=65，Orientation=SE］。同时“视野线”准则中搜索判断函数将扩展为 GoThrough(posA，directionA，posB，directionB)，给定相应的起始和最终方向。另外，对相应的数据结构和改进的启发函数作出说明:

(1)算法的数据结构:转弯策略使用的结构体LineSegment将包含3种离散线段，即1.3.2节中提到的第1段圆弧、中间直线段和第2段圆弧，结构体包含3个成员变量，分别为圆弧标志位、线段长度及起始位置坐标。如果线段是直线，则记录角度;如果线段是圆弧，则记录转弯圆的圆心、圆弧所包含的弧度、圆弧开始角度或结束角度。

(2)改进的启发函数:传统A*算法中采用曼哈顿距离作为启发函数，易造成目标点各方向权值相同而增加搜索时间。因此，采用1.3节中所述的最短曲线路径来替换，从而保证目标方向的权值最大化。

方向A*算法仍以“视野线”平滑步骤顺序进行，在步骤(4)时，首先基于改进的启发函数尝试“圆弧—直线—圆弧”转弯策略的曲线路径，如果成功则用扩展的GoThrough函数检测是否覆盖障碍栅格，继续1.2节中步骤(5)～(7)直至平滑结束，最终获取避免碰撞的最短平滑路径。

1.5 基于二叉堆的加速方法

方向A*算法一般以8邻域搜索，图7中，如果转弯半径过大，不可能在获取a→b→c→d路径的同时不碰到障碍栅格，唯一的方法是获得a→d的直接路径。所以，必须扩大搜索范围，采用24邻域方向A*算法甚至48邻域。这种扩展方法伴随的最大问题是耗时，为此本文将采用一种基于二叉堆的加速方法。

方向A*算法中，在OpenList里搜寻式(1)中拥有最小F值的节点是延缓算法效率的最大问题之一。因此，OpenList中数据的存储方式将直接影响算法速度。二叉堆是完全二叉树，其最小堆的堆序性始终维持根节点最小，从而保证本文算法搜索F值的时间复杂度为O(1)［17］。

图7 8邻域方向A*算法无法识别的路径Fig．7 Legal curved path which cannot be found by directional-8 algorithm

一个合格的二叉堆如图8a所示，为省去指针问题，将其简化成图8b中的一维数组。根节点位置为1(位置0用于标记)，第n个节点的子节点的位置分别为2n+1和2n+2。添加新节点(位置为m)时将其置于数组末端，然后与父节点(位置为(m－1)/2)比较，若小则交换，直至父节点不再比它大或已到达位置1。删除数组第1个节点，然后把最后一个位置的节点置顶，依次与子节点比较直至满足关系。相较传统排序算法的O(n)时间复杂度，上述操作压缩为O(lgn)。

图8 二叉堆结构及数组形式Fig．8 Structures of binary heap and its array form

对于固定尺寸的栅格地图(假设长m、宽n)，方向A*算法所需的二叉堆数组OpenList长度最大为m×n，最小节点为OpenList［1］。该数组存储了扫描节点的F值，但并未给出当前栅格的地图坐标。为此，用下述方法改进:①每次扫描后，增加nodeChecked变量，存入OpenList数组。②将真实F值存入相同大小的Fcost数组，nodeChecked为数组编号。③当前扫描节点的坐标值分别用相同大小的openX和openY数组记录。

图9为更改后的存储结构。

图9 改进的二叉堆结构Fig．9 Structure of improved binary heap

当需要添加新的节点到OpenList中时，计算该点F值，递增NodeChecked和num of OpenList变量，并将已更改的 NodeChecked赋值给数组 OpenList (num of OpenList)。然后与其父亲节点比较Fcost (OpenList())值，若较大则上滤结束，否则交换位置并继续类似比较，直到上滤至合适位置或位置1。

当路径优化到已经搜索的节点时，需要删除最小 F值节点并加入到 CloseList中。将 OpenList (num of OpenList)赋值给OpenList(1)，变量num of OpenList递减。然后与其 2个子节点比较 Fcost (OpenList())值，若其值最小则下滤结束，否则与较小子节点交换位置，继续与新子节点比较直至循环结束。

2 仿真

本文所述算法在计算机(Intel Core i5-4200U处理器，4.00GB RAM)Ubuntu14.04操作系统环境下，基于ROS框架的Stage仿真环境中编程实现。假设单元栅格为边长1m，地图尺寸为20m×20m，机器人本体最大半径为0.4 m，转弯半径为0.5 m，碰撞检测间隔为0.2 m。模拟规划时，起点坐标为(6，15)，终点坐标为(3，17)。

2.1 传统A*算法与方向A*算法性能对比

在模拟地图中，分别使用传统A*算法、“视野线”平滑算法、8邻域方向A*算法和24邻域方向A*算法进行路径规划，优化效果如图10所示。

对比搜索结果可知，“视野线”平滑算法一定程度上减少了路径拐点和过多折线，但并未根据机器人本体信息考虑目标方向，造成A*算法中碰撞点(a～e)依然存在。增加转弯策略的方向A*算法避免碰撞的同时，检测到h点转弯的不合法性，重新规划了路径，从点f出发绕行，通过点g处的右转弯到达目标点。另外，24邻域方向A*算法较8邻域方向A*算法，搜索范围更广，优化了最短路径。

2.2 加速方法对效率的影响

24邻域甚至48邻域方向A*算法固然能符合平滑特性，但搜索范围的增加及转弯策略的应用，大大增加了时间消耗。因此，基于本文提出的加速方法，对图10中的仿真环境，分别对A*算法、8邻域方向A*算法、24邻域方向A*算法和48邻域方向A*算法进行实验验证(表1)。

图10 不同优化方法的路径规划图Fig．10 Path planning graphs of different optimization methods

表1 不同方法的加速前后效率对比Tab．1 Contrast of algorithm efficiency before and after acceleration ms

表1的实验结果表明，基于二叉堆的加速方法能平均提速4～7倍，可以有效提高算法效率，尤其是在方向A*算法扩大邻域搜索范围，使得局部搜索节点大量增加的情况。当前测试地图尺寸只有20m×20m，若该方法应用于实际环境中，提速效果将更为显著。

3 真实环境下的实时路径规划

为验证方向A*算法的可行性，将其用于贝贝机器人本体并在温室模拟地图中进行路径规划及轨迹跟踪试验。机器人贝贝是中国科学院合肥物质科学研究院研发的系统，基于Gmapping方法构建的实际地图及真实场景如图11所示。其中，规划路径的起点为温室入口点A(3.99，－1.38)，目标点为模拟某培养间的点B(－0.99，1.14)。

图11 实际场景及构建地图Fig．11 Actual scene and grid map

图12 实际运行轨迹对比及机器人跟踪误差曲线Fig．12 Comparison between path searched and tracking error curve during tracking test

试验过程中，机器人系统将实时记录方向A*算法规划的路径(图12a中绿色曲线)和实际运行轨迹(图12a中红色曲线)。观察可知，机器人基本按照规划路径成功抵达目标，路线不能重合的地方主要因为机器人转弯时加速度造成的惯性所致。分析实时跟踪数据(图12b)，机器人的实际跟踪误差始终小于0.15m，满足实际需求。

4 结论

(1)针对温室机器人路径规划问题，从生成路径的平滑设计、碰撞检测和算法实时性出发，提出一种方向A*算法，结合“视野线”平滑原则和“圆弧—直线—圆弧”转弯策略，并辅以二叉堆加速方法。

(2)仿真结果表明，相较传统A*算法，方向A*算法的转弯策略及方向性，在平滑路径的同时兼顾了机器人本体的碰撞问题，更加符合实际需求。同时，增加的加速方法也进一步提高效率，保证了算法的实时性。

(3)通过模拟温室环境下的机器人试验，表明真实机器人的路径跟踪误差保持在0.15m以内，验证了本文提出的方向A*算法在温室机器人路径规划中的可行性。

1 ZHOU Zhiping，NIE Yunfeng，GAOMin．Enhanced ant colony optimization algorithm for global path planning ofmobile robots［C］∥2013 5th International Conference on Computational and Information Sciences，2013:698－701．

2 陆新华，张桂林．室内服务机器人导航方法研究［J］．机器人，2003，25(1):80－87．LU Xinhua，ZHANG Guilin．Summarization on indoor service robot navigation［J］．Robot，2003，25(1):80－87．(in Chinese)

3 ZAMIRIAN M，KAMYAD A V，FARAHIM H．A novel algorithm for solving optimal path planning problems based on parametrization method and fuzzy aggregation［J］．Physics Letters A，2009，373(38):34－39．

4 张建英，赵志萍，刘暾．基于人工势场法的机器人路径规划［J］．哈尔滨工业大学学报，2006，38(8):1306－1309．ZHANG Jianying，ZHAO Zhiping，LIU Dun．A path planningmethod formobile robot based on artificial potential field［J］．Journal of Harbin Institute of Technology，2006，38(8):1306－1309．(in Chinese)

5 祝继华，周颐，王晓春，等．基于图像配准的栅格地图拼接方法［J］．自动化学报，2015，41(2):285－294．ZHU Jihua，ZHOU Yi，WANG Xiaochun，etal．Gridmapmerging approach based on image registration［J］．Acta Automatica Sinica，2015，41(2):285－294．(in Chinese)

6 STENTZ A．Optimal and efficient path planning for partially-known environments［C］∥Proceedings of the IEEE International Conference on Robotics and Automation，1994:3310－3317．

7 HU Yanrong，SIMON X Y．A knowledge based genetic algorithm for path planning of a mobile robot［C］∥Proceedings of the 2004，IEEE international Conference on Robotics＆Automation，2004:4350－4355．

8 MOHD M，MATTHEW W，NICHOLASK T．Ant colony robotmotion planning［C］∥Eurocon 2005，IEEE，2005:213－216．

9 王红卫，马勇，谢勇，等．基于平滑A*算法的移动机器人路径规划［J］．同济大学学报:自然科学版，2010，38(11):1647－1650，1655．WANG Hongwei，MA Yong，XIE Yong，et al．Mobile robot optimal path planning based on smoothing A*algorithm［J］．Journal of Tongji University:Natural Science，2010，38(11):1647－1650，1655．(in Chinese)

10 单伟，孟正大．基于改进A*算法的平滑路径设计［J］．东南大学学报:自然科学版，2010，40(增刊1):155－161．SHANWei，MENG Zhengda．Smooth path design for mobile servise robots based on improved A*algorithm［J］．Journal of Southeast University:Natural Science Edition，2010，40(Supp．1):155－161．(in Chinese)

11 BOISSONNAT JD，CEREZO A，LOBLOND J．Shortest paths of bounded curvature in the plane［C］∥Proceedings of the IEEE International Conference on Robotics and Automation，1992:2315－2320．

12 TROCATO K I，DORST L．Differential A*［J］．IEEE Transactions on Knowledge and Data Engineering，2002，14(6):1218－1229．

13 王殿君．基于改进A*算法的室内移动机器人路径规划［J］．清华大学学报:自然科学版，2012，52(8):1085－1089．WANG Dianjun．Indoor mobile-robot path planning based on an improved A*algorithm［J］．Journal of Tsinghua University: Science and Technology，2012，52(8):1085－1089．(in Chinese)

14 周文卷．复杂环境下自主移动机器人路径规划方法的研究［D］．长春:吉林大学，2014．

15 GIUSEPPEE C，MARCELLO F，GIACOMO L．A network flow based heuristic approach for optimising AGV［J］．Journal of Intelligent Manufacturing，2013，24(2):405－419．

16 马飞，杨皞屾，顾青，等．基于改进A*算法的地下无人铲运机导航路径规划［J/OL］．农业机械学报，2015，46(7):303－309．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?file_no=20150743＆flag=1．DOI:10．6041/j．issn．1000-1298．2015．07．043．MA Fei，YANG Haoshen，GU Qing，et al．Navigation path planning of unmanned underground LHD based on improved A*algorithm［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2015，46(7):303－309．(in Chinese)

17 杨泳，户佐安，何金海．路径诱导系统中双向启发式A*算法研究［J］．计算机工程与应用，2014，50(16):54－56，71．YANG Yong，HU Zuoan，HE Jinhai．Research of bidirectional heuristic A*algorithm in route guide system［J］．Computer Engineering and Applications，2014，50(16):54－56，71．(in Chinese)

Real-time Path Planning of Greenhouse Robot Based on Directional A*Algorithm

ZHANGWen1，2LIU Yong1ZHANG Chaofan1，2ZHANG Long1XIA Yingwei1
(1．Institute of Applied Technology，Hefei Institutes of Physical Science，Chinese Academy of Sciences，Hefei230031，China 2．University of Science and Technology of China，Hefei230026，China)

Because of the existing problems in path planning of greenhouse robot under complex environment，a directional A*algorithm was proposed．Thismethod was focused on the smooth design，collision detection and the algorithm efficiency．Firstly，the“line of sight”solutionswere used to smooth the path for getting rid of the zigzag effect and collisions．Secondly，the“arc-line-arc”turningmethods were applied to avoid thewidth of the greenhouse robot in path finding．At last，some basic optimizations based on the binary heap were carried out to speed up the directional A*algorithm．Simulation and comparison results between the improved A*algorithm and traditional one showed that the proposed method wasmore efficient．It can not only meet the requirements of smooth，but also predict collision after proceeding with turning strategy．At the same time，the accelerating algorithm based on the binary heap made the path finding 4～7 times faster．Moreover，a path planning and tracking test was carried out in laboratory environment，where a simulation greenhouse was built．The results verified that the tracking precision can keep in a small range and the greenhouse robot can run without collision when the navigation path was given by the proposed algorithm，which proved the effectiveness and feasibility of the directional A*algorithm．

greenhouse robot;path planning;directional A*algorithm;binary heap

TP242.6

A

1000-1298(2017)07-0022-07

2016-11-16

2016-12-11

“十二五”国家科技支撑计划项目(2015BAI01B00)、安徽省科技重大专项计划项目(15CZZ02019)和安徽省创新型省份建设专项资金项目(15CZJ07008)

张文(1987—)，男，博士生，主要从事机器人视觉研究，E-mail:zhangwen@aiofm．ac．cn

夏营威(1985—)，男，副研究员，博士，主要从事机器视觉及机器人研究，E-mail:xiayw@aiofm．ac．cn

10．6041/j．issn．1000-1298．2017．07．003