五轴联动铣削复杂曲面表面粗糙度研究*

陈 冲，尹韶辉，杨 婷，周飞轮

(湖南大学 国家高效磨削工程技术研究中心，长沙 410082)



五轴联动铣削复杂曲面表面粗糙度研究*

陈 冲，尹韶辉，杨 婷，周飞轮

(湖南大学 国家高效磨削工程技术研究中心，长沙 410082)

为了提高五轴联动铣削复杂曲面的加工质量，分析多切削工艺参数对表面粗糙度的影响至关重要。首先，通过单因素实验分析了各切削工艺参数对表面粗糙度的影响规律，基于模拟退火算法理论，分别建立了各切削工艺参数与表面粗糙度的一元关系模型；其次，通过对单因素实验数据进行归一化处理，为正交实验优选切削工艺参数区间；最后，通过正交实验，分别建立了基于模拟退火及传统最小二乘原理的表面粗糙度多元复合预测模型并通过实验进行验证。验证结果表明，所建立的预测模型能够为复杂曲面铣削加工优选加工参数提供更准确的指导。

五轴联动铣削；复杂曲面；表面粗糙度

0 前言

随着对机械加工件要求的不断提高，空间复杂曲面的高效高精加工成为亟待解决的问题，五轴联动数控加工中心应运而生。相较于三轴铣削来说，五轴联动铣削提高了切削加工的加工范围和加工零件的复杂度及精度，缩短了加工工序。因此，广泛应用于航空航天，船舶制造以及大型复杂模具的精密加工等领域[1]。

表面粗糙度是评定五轴联动铣削加工后表面特征及加工特性的重要参数。表面粗糙度不仅可以分析和评价加工后零件的表面质量而且可作为重要的加工参数去控制切削过程中各切削工艺参数[2]。此外，零件的表面粗糙度也可以综合反映出切削后工件的物理和力学性能、疲劳强度以及工件之间的配合性能等[3]。

对于五轴联动数控加工而言，影响表面粗糙度的因素很多，单纯通过线性推导不能建立准确的表面粗糙度预测模型。模拟退火算法作为一种启发式的智能优化算法擅长全局最优解的搜索并且能有效避免算法最终收敛于局部最优解[4]。通过采用模拟退火算法可以得到较线性优化模型更好的表面粗糙度预测模型。五轴联动铣削由于其加工工艺参数多，加工过程中影响因素复杂，若采用人工神经网络预测，则解空间将异常复杂并且存在所建网络内部单元意义含糊、收敛时间长等缺点，因此不适合多切削工艺参数的建模，模拟退火算法可以得到更优化的表面粗糙度预测模型[5-6]。

表面粗糙度预测模型在三轴机床上已经建立并且对提高加工质量起到了很好的指导作用。然而，对于五轴联动数控加工中心铣削复杂空间曲面的表面粗糙度预测模型研究的还很少[7-8]并且在研究的过程中考虑的影响因素也不够全面和具有代表[9]。因此，研究五轴联动数控加工中心铣削复杂空间曲面的预测模型对于提高铣削空间复杂曲面的加工质量至关重要。

本文利用五轴联动数控加工中心铣削空间复杂曲面。首先，依据单因素实验，分析了表面粗糙度的影响机理并通过1STOPT软件集成的模拟退火算法建立一元表面粗糙度预测模型。其次，利用归一化处理优选切削工艺参数。最后，通过正交实验进一步建立多元表面粗糙度预测模型并通过对比传统最小二乘法建立的多元预测模型。最终确认SA所建立的预测模型能够更好地优选切削参数，提高铣削复杂曲面的加工质量。

1 五轴联动铣削单因素实验

通过五轴联动铣削铝合金6061，分析了表面粗糙度的影响因素，建立表面粗糙度一元预测模型并优选正交实验切削参数区间。

1.1 实验条件

工件材料选用铝合金6061，其化学成分及力学性能如表1、表2所示[10]。

表1 铝合金6061化学成分

表2 铝合金6061力学性能

加工机床为德国德玛吉公司的DMU60五轴联动数控加工中心，试件为φ100mm棒料铝合金。刀具为φ16mm的硬质合金可拆卸球头铣刀，型号为KDMB16MOERLD，切削液冷却，实验机床及刀具如图1所示。表面粗糙度测量用北京凯达仪器厂生产的手持式表面粗糙度仪。

图1 五轴机床及铣削刀具

1.2 实验方案

单因素实验，为保证切削条件一致， 采用固定的引导角保证刀具接触点位置不变。为尽量消除刀具磨损所带来的误差，每6组实验更换新刀具。为使得在复杂曲面上测得的表面粗糙度尽可能反映真实的表面粗糙度，采用在复杂曲面上三个不同位置所得值的平均值作为每一次的测量值。单因素铣削实验参数如表3所示。

表3 单因素实验参数

所加工的空间复杂曲面的模型如图2所示，以用户坐标系为参考坐标系曲面的方程如式(1)所示。

Z=8.76x2-1.78y2

(1)

图2 空间复杂曲面模型

1.3 表面粗糙度的影响因素及机理分析

对于模拟退火算法来说，较高初始的温度以及较长的Mapkob链长度可以保证算法得到较为精确的搜索结果，而冷却系数越接近1则全局搜索得越细致，模拟退火的单因素数值拟合参数设置如表4所示。

表4 模拟退火算法单因素建模参数设置

1.3.1 切削速度对表面粗糙度的影响

通过模拟退火算法可以获得切削速度vc与表面粗糙度Ra的关系模型表达式如下：

(2)

式中，模型决定系数为0.941。

表面粗糙度Ra的实测值与SA拟合值如图3所示。

图3 切削速度vc拟合曲线

图中显示，随着切削速度vc的增大表面粗糙度先减小而后缓慢上升，vc=170m/min为拐点。在切削过程中，当实际切削速度较小时，切屑的形成主要依靠前刀面的挤压作用。随着切削速度的逐渐增大，缩短了切屑与前刀面的挤压作用时间，使得切屑被铣刀很快切离工件表面。最终导致切削力下降，提高了加工工件表面的质量。当切削速度过了拐点之后，由于机床的振动及刀具的磨损，使得表面粗糙度数值重新增大，工件表面加工质量恶化。所以，应该在vc=170m/min附近优选切削速度。

1.3.2 每齿进给量对表面粗糙度的影响

同理，每齿进给量fz与表面粗糙度的关系模型可表示如下：

(3)

式中的模型决定系数为0.994。

表面粗糙度Ra的实测值与SA拟合值如图4所示。

图4 每齿进给量fz拟合曲线

图示显示，随着每齿进给量fz增大，表面粗糙度Ra先缓慢上升而后在fz=0.12mm/z附近随着fz增大而急剧上升。当每齿进给量较小时，单次切削量较小，切削力不大，表面粗糙度数值较小。当每齿进给量较大时，单次切削量增大，切削力急剧增大，切削热增多，最终导致表面粗糙度数值快速增大。

1.3.3 切削深度对表面粗糙度的影响

切削深度ap与表面粗糙度的关系模型可以表示如下：

(4)

式中的模型决定系数为0.993。

表面粗糙度Ra的实测值与SA拟合值如图5所示。

图5 切削深度ap拟合曲线

图示显示，随切削深度ap的增大表面粗糙度Ra整体上呈现先减小后增大的趋势，当切削深度较小时，工件加工表面以挤压及划擦等塑性变形的方式产生切屑，表明粗糙度数值较小。当切削深度有较大增加时，切削力急剧增大，刀具震颤加大，表面加工质量恶化。ap=0.15mm时因共振出现突变点。

1.3.4 行距对表面粗糙度的影响

行距h与表面粗糙度的关系模型可以表示为：

Ra=0.1236h1.6786e11.7722h+0.3013

(5)

式中的模型决定系数为0.995。

表面粗糙度Ra的实测值与SA拟合值如图6所示。

图6 行距h拟合曲线

图示显示，随着行距h的增大，表面粗糙度Ra缓慢上升后急剧上升，拐点在h=0.235mm附近。行距增大即残留高度增加，过渡表面再次被切除的量将变大，导致切削力增大，切削热增多，表面粗糙度数值变大。较小的行距可保证加工质量，但切削效率不高，故应综合考虑优选行距。

1.4 切削工艺参数的优选

由于各铣削工艺参数不同，所以各切削参数的优选必须有统一的评价标准。故对各工艺参数进行归一化处理[11]。

各工艺参数的归一化处理公式如下：

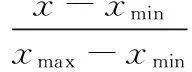
(6)

其中，x、y分别为归一化前后的数值，xmin、xmax为样本数据的最小和最大值。

将各切削工艺参数归一化处理，综合考虑加工效率和表面质量，优选切削工艺参数用于正交实验。切削速度vc、每齿进给量fz、切削深度ap及行距h归一化之后如图7所示。相应地，切削工艺参数的优选区间和对应的优选的工艺参数区间如表5所示。

图7 切削工艺参数归一化数值

铣削工艺参数优选区间优选工艺参数区间vc(m/min)0.4～0.7158～239fz(mm/z)0～0.60.01～0.088ap(mm)0～0.80.05～0.41h(mm)0～0.40.04～0.164

2 五轴联动铣削正交实验

2.1 实验条件

工件材料采用铝合金6061，机床，刀具、铣削方式、冷却方式、测量仪器及测量方式均与单因素实验相同。铣削过程及铣削后的铝合金表面如图8所示。

(a)铣削 (b)铣削后铝合金表面

2.2 正交实验设计及测量结果

如表6所示为优选的正交实验切削工艺参数及相应的表面粗糙度Ra的数值，建立4因素3水平的正交试验表如下。

表6 正交实验切削工艺参数

运用模拟退火算法擅长全局粗搜索和局部精搜索的特点，进行多元表面粗糙度模型的建立，模拟退火算法的参数设置如表7所示。

表7 模拟退火算法多因素建模参数设置

通过模拟退火算法最终获得切削速度vc、每齿进给量fz、切削深度ap及行距h与表面粗糙度Ra的多元表面粗糙度预测模型如下：

e-13.9232vc fz ap h+ 0.2658

(7)

模型决定系数为0.983，运用传统最小二乘原理(least-square简称L-S)，通过MATLAB非线性拟合函数nlinfit，基于已有的模型公式，建立的表面粗糙度预测模型如式(8)所示。

e0.6041vc fz ap h+ 0.256

(8)

正交实验表面粗糙度Ra实测值与SA和L-S所建模型的拟合值如图9所示。

图9 实测值与SA及L-S预测模型拟合值对比

由图9可得，SA算法建立的多元表面粗糙度预测模型较传统L-S所建的预测模型能更好地与正交实验的表面粗糙度实测值匹配。

2.3 模型预测准确度验证

随机选取6组切削参数进行铣削试验对所建立的表面粗糙度模型进行预测准确度验证。验证结果如表8所示，表面粗糙度Ra实测值与SA和L-S所建模型的预测值如图10所示。

表8 表面粗糙度模型预测准确度验证

图10 实测值与SA及L-S预测模型拟合值对比

预测结果表明，模拟退火算法擅长全局搜索，尤其是非线性优化全局搜索，所建立的表面粗糙度预测模型误差百分比最大不超过5%，达到了较为理想的预测结果，符合要求。相比之下，传统最小二乘法所建立的预测模型与实际情形误差较大，不符合工程实际的要求。

3 总结

(1)通过五轴联动铣削单因素实验，从机理上分析了表面粗糙度Ra与各切削工艺参数组合内在联系并基于模拟退火算法理论建立了各切削工艺参数与表面粗糙度的一元关系模型。以模型决定系数R为评价标准，检验了模型的可靠性，结果表明所建模型具有较高的可靠度。

(2) 通过对单因素实验数据进行归一化处理，优选出各切削工艺参数合理的取值区间，为正交实验优选切削工艺参数提供参考。

(3) 基于模拟退火算法理论，通过五轴联动铣削正交实验，建立了表面粗糙度与各切削工艺参数的多元复合预测模型并与传统最小二乘法所建立的多元预测模型进行了对比。对比结果表明，在预测实验中，SA所建立的多元模型的预测值与实测值的最大误差为4.138%，而L-S所建立的多元模型预测值与实测值最大误差达到37.6%。SA算法所建模型能更好的为复杂曲面铣削优选出切削参数，从而提高复杂曲面铣削的加工质量。

[1] 陆启建,褚辉生. 高速切削与五轴联动加工技术[M].北京：机械工业出版社,2011.

[2] 魏杰,李耀明,张煌,等. 基于SIED深孔钻表面粗糙度影响因素的研究[J].组合机床与自动化加工技术,2016(8):19-20.

[3] 杨翠蕾,郑清春,胡亚辉,等. 车削钛合金 TC4 的表面粗糙度预测模型构建[J].组合机床与自动化加工技术,2016(6):128-129.

[4] Azlan Mohd Zain，Habibollah Haron，Safian Sharif. Integration of simulated annealing and genetic algorithm to estimate optimal solutions forminimising surface roughness in end milling Ti-6AL-4V[J]. International Journal of Computer Integrated Manufacturing, 2011, 24(6):574-592.

[5] Gabriel Medrado Assis Acayaba, Patricia Munõz de Escalona. Prediction of surface roughness in low speed turning of AISI316 austenitic stainless steel [J]. CIRP Journal of Manufacturing Science and Technology, 2015, (11):62-67.

[6] M Madiéa, M Radovanoviéa, B Nedié.Modeling andSimulated Annealing Optimization of Surface Roughness in CO2Laser Nitrogen Cutting of Stainless Steel[J]. Tribology in Industry, 2013,35(3):167-176.

[7] G Mahesh,S Muthu,S R Devadasan. Prediction of surface roughness of end milling operation using genetic algorithm [J]. Int J Adv Manuf Technol,2015,77:369-381.

[8] 刘牧,杨茂奎,霍颖.复杂曲面五坐标数控铣削表面粗糙度预测的关键技术研究[J].机械制造,2005, 43(495):12-14.

[9] 李灵光,王爱民,王小龙.航空铝合金三维端铣表面粗糙度的LS-SVM控制研究[J].机械设计与制造,2015 (3):256-259.

[10] 邱铖铖, 徐兴昂,叶婷婷,等. 6061 和 6066 铝合金时效与冷变形的组织与性能研究[J].热加工工艺,2016, 45(16):235-237.

[11] 刘维伟,李锋,任军学,等.基于标准粒子群算法的高速铣削表面粗糙度研究[J].中国机械工程,2011, 22(22):2654-2657,2771.

(编辑 李秀敏)

Study on Complex Surface′s Roughness in Five-axis Milling

CHEN Chong,YIN Shao-hui,YANG Ting,ZHOU Fei-lun

(National Engineering Research Center for High Efficiency Grinding,Hunan University,Changsha 410082,China)

Analyzing the effect of cutting parameters on surface roughness is crucial to improve the milling quality of complex surface with five-axis CNC machining center. Firstly, single factor experiments are employed to analyze influence principle of cutting parameters on surface roughness. Numerical models between cutting parameter and surface roughness are established respectively by using simulated annealing(SA). Secondly, optimization of cutting parameters’ range is carried out for orthogonal experiments by normalizing the data of single factor experiments. Lastly, through orthogonal experiments, multivariate predictive models of surface roughness, based on the algorithms of simulated annealing(SA) and least-square(L-S), are constructed respectively and verified. Result shows that the predictive model may provide more accurate guidance for optimizing cutting parameters of complex surface milling.

five-axis milling；complex surfaces；surface roughness

1001-2265(2017)07-0073-04

10.13462/j.cnki.mmtamt.2017.07.017

2016-09-18；

2016-11-10

蓝宝石晶片高效率高精度磨抛加工关键技术合作研究(2014DFG72480)

陈冲(1990—)，男，安徽滁州人，湖南大学硕士研究生，研究方向为超精密及微纳制造技术与装备，(E-mail)cc099054001@163.com；尹韶辉(1967—)，男，长沙人，湖南大学教授，博士研究生导师，博士，研究方向为超精密及微纳制造技术与装备，(E-mail)shyin2000@hotmail.com。

TH16;TG65

A