基于FCM改进遗传算法的工字梁多目标优化设计*

张 屹，李子木，余 振，杨宇琪

(三峡大学 机械与动力学院，湖北 宜昌 443002)



基于FCM改进遗传算法的工字梁多目标优化设计*

张 屹，李子木，余 振，杨宇琪

(三峡大学 机械与动力学院，湖北 宜昌 443002)

为了对工字梁结构进行优化设计，建立了以工字梁横截面积最小和给定负载条件下的最小化静挠度最小为目标函数，以满足梁的弯曲强度条件及截面尺寸限制条件为约束条件的多目标优化模型，并提出了一种基于模糊C均值聚类改进的多目标优化算法来对其进行求解。该算法利用FCM的模糊划分和最大隶属度来对交配选择过程进行交配约束限制。将该算法与其他典型的多目标优化算法在GLT系列测试函数上进行对比测试，结果表明所提出的算法性能更好，能得到具有更好收敛性且分布更均匀的Pareto前端。工字梁实例的求解也证明了该算法的优良性及实用性。

工字梁；多目标优化设计；模糊C均值聚类

0 引言

工字梁是一种工字形断面的组合梁，其具有重量轻、抗弯刚度大、结构简单等优点，被广泛地用于各种建筑工程、重型机械等领域。工字梁能在节省大量材料的同时获得几乎近似于外轮廓一样的矩形截面惯性矩，因而能承受很大的弯矩。工字梁的腹板是四边简支板，翼板则为三边简支一边自由，其截面尺寸设计需要考虑强度和稳定性是否满足基本的安全要求。

近年来，关于工字梁的优化设计研究有许多。陈振等[1]通过分析工字梁主要的破坏形式，找到对应不同破坏形式的主要影响因素，进而得到合理的结构优化设计的理论依据。王瑶瑶等[2]采用外点法罚函数的数学优化方法对工字梁进行优化设计，加快收敛速度，缩短了计算时间。卢超[3]则通过改进的元胞遗传算法对工字梁进行多目标优化设计，也取得了不错的效果。本文利用基于FCM改进的遗传算法来求解工字梁多目标优化设计问题，将模糊C均值聚类(FCM)应用到遗传算法的交配选择过程，得到一种基于模糊C均值聚类(FCM)进行交配约束限制的多目标优化算法。然后，将改进的算法与其它经典的多目标优化算法进行性能比较。最后，将该算法用于工字梁的多目标优化设计，并与普通的优化方案作对比，验证算法的优越性，为工字梁的多目标优化设计提供一定的依据。

1 工字梁优化模型

1.1 设计变量的选择

工字梁的结构优化主要是截面尺寸的优化[4]，其优化设计参数有工字梁整体高度a，翼板的宽度b，腹板的厚度c和翼板的厚度d。于是确定优化设计变量为x=[x1,x2,x3,x4]T=[a,b,c,d]T。工字梁结构如图1所示。

图1 工字梁结构

1.2 目标函数的建立

(1) 横截面积最小

在工字梁的结构优化设计中，往往需要尽可能地节省耗材，因为耗材的多少决定着生产成本的高低。因此从降低生产成本的角度考虑，将工字梁的横截面积最小作为优化目标之一，其表达式可由四个决策变量表示为：

minf1(x)=2x2x4+x3(x1-2x4)

(2) 最小化静挠度最小

在减少耗材的同时还需要考虑工字梁的稳定性和强度，可采用静挠度来综合衡量其稳定性和强度。因此，在给定负载条件下的最小化静挠度最小可作为另一优化目标，最小化静挠度的公式为：

其中，P为最大弯曲载荷，l为工字梁长度，E为杨氏弹性模量，I为惯性矩。此处的惯性矩I可由决策变量表示为：

1.3 约束条件的确定

根据相关的设计要求，工字梁的优化设计需要满足以下约束条件。

(1)弯曲强度的条件限制

要保证工字梁所受的弯曲应力小于梁的许用弯曲应力，即有：

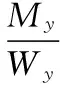
其中，My和Mz分别为Y轴和Z轴方向上的最大弯矩，Wy和Wz分别是Y轴和Z轴方向上的抗弯截面系数，[σ]为梁的许用弯曲应力。抗弯截面系数又可根据所设的决策变量表示如下：

故第一个约束条件为：

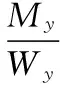
(2)截面尺寸的条件限制

根据不同的设计条件和需求，对于截面的尺寸有不同的限制，即有约束条件为：

其中，amin,amax,…,dmin,dmax分别为针对实际情况所设定的尺寸上下限。

2 基于FCM改进的遗传算法

近年来，聚类技术发展迅猛，被广泛地应用于数据挖掘、统计学以及机器学习等领域。聚类技术可笼统地分为硬聚类与软聚类两大类，所谓的硬聚类，即每一个个体只能被归为一类；所谓的软聚类，即通过隶属度来确定每个个体隶属于各个类的程度的模糊聚类。本文所提出的遗传算法FCMMO就是利用模糊C均值聚类来进行交配约束的多目标优化算法。

模糊C均值聚类(FCM)[5]是一种实现模糊划分的聚类方法，其主要是被用来最小化以下函数：

式中，m是一个指定模糊度的实数参数，υj是第j个聚类的中心，V={υ1,υ2,…,υC}是一系列聚类的中心，||·||代表任何一个数据点和聚类中心之间的距离的规范表示，其中μij为第i个个体对于第j个类的隶属度，其表达式为：

基于这种FCM聚类算法，本文提出了一种交配约束限制(FMR)方案来为每一代个体xi设置交配池Qi，具体伪代码如下：

Qi=FMRxi,P,U()①If∑k-1j=1μij≤rand()≤∑k+1j=1μij, 1≤k≤C do②Gathersolutionsinthekthclusterbasedonmaximummembershipprinciple,CT=xqk=argmaxl∈1,…,C{}μql, q∈1,…,N{}{}.③Setthematingpoolforxi, Qi=CT if CT≥2P otherwise{.④endif⑤returnQi.

确定交配池后，通过二进制锦标赛选择机制[6]确定父代，再采用差分进化[7]和多项式变异[8]操作来对父代进行交叉变异操作生成新一代个体。在这个过程中，首先通过差分进化算子生成一个试验解y′；然后在y′上施加一个边界修复机制，使其成为可行解；接着采用多项式变异算子对可行解进行变异操作，进一步提高其质量；最后，再次采用相同的修复机制来确保变异后的解是可行解。具体伪代码如下：

y=SolutionGenerationx,Q()①Choosetwodifferentparentsolutionsxr1,xr2fromQbybinarytournamentselectionapproach.②Generateatrialsolution y'=x+F×xr1-xr2().③Repairthesolutiony″i=aiify'ibiy'otherwiseìîíïïïï,whereaiandbi,i=1,2,…,n,denotethelowerandupperboundariesoftheithvariable,respectively.④Mutatethesolution y‴i=y″i+δi×bi-ai() if rand()biy‴i otherwiseìîíïïïï,for i=1,2,…,n.⑥returny=y1,y2,…,yn()T.

具体算法流程如下：

该电影产业大数据可视化Hybrid App支持跨平台，本章对软件在多个平台上进行了测试，测试设备是基于Android系统的小米3手机和基于iOS系统的iPhone 7手机，测试真机参数如表1所示。

Step1：算法参数设置：种群大小N，最大迭代次数T，聚类个数C，差分控制参数F和CR，多项式变异概率Pm和变异的分布指数ηm等；

Step2：种群初始化并建立一个空的外部档案；

Step3：设置迭代计数器t=1；

Step4：利用FCM发现种群个体的聚类结构；

Step5：对每个个体按照文中提出的FMR设置交配池，利用锦标赛选择机制选出父代个体；

Step6：通过差分进化策略和多项式变异操作得到子代个体；

Step7：评估子代个体，更新当前种群和外部档案；

Step8：更新计数器t，判断其是否达到所设的最大

迭代次数。若是，输出外部档案作为最优的Pareto前端，反之转到Step4。

3 算法性能测试与分析

为了更好地测试本文所提出的算法性能，将该算法与MOEA/D-DE[9]，NSGA-II[10]，SMS-EMOA[11]这3种性能良好的算法在具有复杂PF形状和PS结构的GLT[12]系列测试函数上进行测试，并在相同的评价指标下对各算法的性能进行对比评估分析。

3.1 算法评价指标

为了定量地评价算法的性能，本文采用了两种常用的性能评价指标即反向世代距离(IGD)与超体积(HV)来评价该算法的性能。

(1) 反向世代距离(IGD)

假设P*代表一组均匀分布在PF上的Pareto最优解，P是所获得的近似解组成的近似PF，那么反向世代距离(IGD)可定义如下[13]：

(2) 超体积(HV)

超体积(HV) 的定义如下[14]：

3.2 算法参数设置

为了确保对比实验更加公平更加客观，所有算法均采用协调优化后的最佳参数进行对比实验研究，且所有算法均通过MATLAB实现。

参数设置如下：种群大小N=100；变量维度n=10；最大迭代次数T=300；四种算法均采用相同的多项式变异控制参数即pm=1/n,ηm=20；MOEA/D-DE的差分算子最优参数为F=0.3，CR=0.8；而NSGA-II和SMS-EMOA的最优差分算子参数为F=0.5,CR=1；FCMMO的各项参数为C=7,F=0.5,CR=1。

3.3 测试结果与分析

将四种算法分别对GLT系列测试函数进行20次独立运算，统计所得IGD和HV的平均值和标准差，用深灰底纹表示最优值，浅灰底纹表示次优值，具体结果见表1和表2。

表1 反向世代距离(IGD)平均值与标准差

表2 超体积(HV)平均值与标准差

由上述两表可知，针对IGD指标值，FCMMO包揽了所有最优值，其余三个算法分别占了2个次优值；对于表2中的HV指标值，FCMMO依然占据了所有最优值，SMS-EMOA占了5个次优值，NSGA-II则一个也没有。这表明FCMMO相对于其他三种算法来说其性能最好，能获得收敛性、多样性及均匀性都更好的Pareto前端。

4 工字梁实例求解

现对某工字梁问题进行优化设计，已知梁的许用弯曲应力为[σ]=20kN/cm2，杨氏弹性模量为E=2×104kN/cm2，两个最大弯曲载荷分别为P=600kN和Q=80kN，两个最大弯矩分别是My=3000kN·cm和Mz=2800kN·cm，梁的长度为L=200cm，四个决策变量的上下限分别为[10,50],[10,30],[1,10],[1,10]。要求在满足设计要求的情况下，使得梁的横截面最小且在给定负载条件下的静挠度最小。

针对上述工字梁实例，运用前面所提到的三种经典算法与FCMMO对其进行求解。对于该实际问题对算法进行参数优化，最终的参数设置如下：种群大小N=100，外部档案也为100，最大评价次数为Gmax=30000，FCMMO的各项最优参数为C=3,F=0.9,CR=0.6，其他算法的参数通过优化后基本与3.2中设置相同。

图2 NSGA-II得到的Pareto前端

图3 FCMMO得到的Pareto前端

图2和图3分别给出了NSGA-II和FCMMO所得到的Pareto前端，由两个图对比可知，FCMMO得到的Pareto前端的分布性和收敛性都明显优于NSGA-II。

为了更加直观地验证FCMMO的性能，本文比较了各算法所求的子目标的最小值，即上图所示横、纵坐标最小的点A和B。四种算法的子目标最小值及其所对应的决策变量值具体如表3所示，粗体表示最优值。

表3 工字梁设计问题的对比结果

从上表可知，FCMMO所得到的两个最小值均优于其他三个算法。由此可见，通过采用FCMMO来求解工字梁多目标优化设计问题，能在满足弯曲强度条件及尺寸限制条件的约束下，使得到的工字梁结构横截面积更小、最小静挠度更小。

5 结论

本文将模糊C均值聚类(FCM)加入到多目标优化算法中，设计了一种基于模糊C均值聚类的交配约束限制策略(FMR)，并提出了一种基于模糊C均值聚类的多目标进化算法(FCMMO)。在每一次迭代中，FMR采用模糊C均值聚类算法来发现种群个体的聚类结构，然后基于该聚类结构，根据每个个体对聚类的隶属度为其确定相应的交配池进而交叉重组产生新的个体。

性能测试结果表明，FCMMO相较于其他三种经典算法，所得到的Pareto前端分布更加均匀。运用该算法求解工字梁的多目标优化设计，所得结果也相对更优。综上，在求解这类简单的多目标优化问题时，FCMMO具有一定的工程实用价值。

[1] 陈振, 王俊华, 高翔, 等. 起重机工字型截面梁结构优化设计探讨[J]. 港口装卸, 2014 (6): 17-20.

[2] 王瑶瑶, 李松岩, 曹尔卓, 等. 罚函数在复合材料工字梁优化设计中的应用[J]. 纤维复合材料, 2013, 30(3): 30-32.

[3] 卢超. 多目标元胞遗传算法的改进研究及其在工程优化中的应用[D]. 宜昌:三峡大学, 2013.

[4] Coello Coello C A, Christiansen A D. MOSES: A multiobjective optimization tool for engineering design[J]. Engineering Optimization, 1999, 31(3): 337-368.

[5] Takahama T, Sakai S. Fuzzy c-means clustering and partition entropy for species-best strategy and search mode selection in nonlinear optimization by differential evolution[C]//Fuzzy Systems (FUZZ), 2011 IEEE International Conference on. IEEE, 2011: 290-297.

[6] Goldberg D E, Deb K. A comparative analysis of selection schemes used in genetic algorithms[J]. Foundations of genetic algorithms, 1991, 1: 69-93.

[7] Li H, Zhang Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 284-302.

[8] Deb K, Beyer H G. Self-adaptive genetic algorithms with simulated binary crossover[J]. Evolutionary Computation, 2001, 9(2): 197-221.

[9] Zhang Q, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on evolutionary computation, 2007, 11(6): 712-731.

[10] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.

[11] Beume N, Naujoks B, Emmerich M. SMS-EMOA: Multiobjective selection based on dominated hypervolume[J]. European Journal of Operational Research, 2007, 181(3): 1653-1669.

[12] Gu F, Liu H L, Tan K C. A multiobjective evolutionary algorithm using dynamic weight design method[J]. 2012.

[13] Zhang Q, Zhou A, Jin Y. RM-MEDA: A regularity model-based multiobjective estimation of distribution algorithm[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 41-63.

[14] Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE transactions on Evolutionary Computation, 1999, 3(4): 257-271.

(编辑 李秀敏)

A FCM Based Genetic Algorithm for I-Beam Optimization Design

ZHANG Yi，LI Zi-mu，YU Zhen，YANG Yu-qi

(College of Mechanical&Power Engineering，China Three Gorges University，Yichang Hubei 443002，China)

To optimize the design of an I-beam, the paper took the minimization of the cross-sectional area of the I-beam and the minimum static deflection that under given load condition as the objective functions, established the model for the multi-objective optimization and under that the I-beam structure meet the needs for bending strength and sectional size limitation and others．An improved multi-objective optimization algorithm based on fuzzy C-means clustering was proposed. The algorithm uses the fuzzy partition of FCM and the maximum membership degree to constrain the mating selection process. The comparative performance test results on a set of test instances(GLT) reveal that the proposed algorithm outperforms some state-of-the-art algorithms in terms of convergence and diversity．The I-beam example also proved the superiority and practicality of the algorithm.

I-beam; multi-objective optimization design; fuzzy C-means clustering

1001-2265(2017)07-0068-05

10.13462/j.cnki.mmtamt.2017.07.016

2016-12-18

国家自然科学基金项目(51275274，71501110)；三峡大学研究生科研创新基金(SDYC2016032)

张屹(1976—)，男，兰州人，三峡大学教授，博士后，研究方向为智能算法及其机械工程优化应用，(E-mail)jxzhangyi1976@126.com。

TH166;TG506

A