直角坐标机器人悬臂结构优化设计与分析*

朱福康，刘 毅，董 航，孟凡杰，丛 明

(1.大连理工大学 机械工程学院，辽宁 大连 116024；2.营口金辰机械股份有限公司 电气技术部，辽宁 营口 115000)



直角坐标机器人悬臂结构优化设计与分析*

朱福康1，刘 毅1，董 航1，孟凡杰2，丛 明1

(1.大连理工大学 机械工程学院，辽宁 大连 116024；2.营口金辰机械股份有限公司 电气技术部，辽宁 营口 115000)

提出了一种针对工程实际问题的拓扑优化设计方法，对直角坐标机器人悬臂结构进行了拓扑优化设计和力学性能分析。先对整机进行了有限元分析，找出了影响整机精度的关键结构即Y轴悬臂梁。后采用变密度法对悬臂梁横截面进行了拓扑优化，重构筋肋分布，根据优化后的截面形状重建三维模型并进行了力学性能有限元分析。优化前后对比分析结果表明：优化后的悬臂结构的变形减小，最大应力明显降低，结构的质量也显著减轻。该方法对以后机械结构分析和拓扑优化设计具有一定的指导意义。

直角坐标机器人；悬臂梁；有限元分析；拓扑优化

0 引言

随着现代制造业对生产效率和自动化程度要求的提高，工业机器人[1]的大量应用已经成为了不可逆转的趋势。直角坐标机器人[2]因结构简单，运动精度高，性能稳定，价格便宜等原因被广泛应用于焊接、搬运、喷涂、装配等工作中。悬臂件作为悬臂式直角坐标机器人的关键结构部件，在整机的静、动态性能方面起着至关重要的作用。采用传统的设计方法[3]虽然能借鉴已有的结构设计出符合要求的悬臂件，但面对缩短设计周期，减少开发成本，便于更新换代等现代机械的设计要求，传统设计手段已无法满足。因此，寻求更高效、精确的现代设计方法成为了解决这一问题的关键。利用现代设计手段可以在计算机环境下实现悬臂结构的建模、仿真等操作，快速地设计出高刚度、轻量化的悬臂结构[4]。

20世纪初期，国外学者Michell[5]在桁架理论中首次提出了拓扑优化的概念，用解析分析的方法得出了最优的桁架结构，被认为是拓扑优化理论研究的里程碑。随后人们将数值分析法应用于拓扑优化设计中，使得连续体拓扑优化理论迅猛发展，形成了均匀化方法 、变密度法 、结构渐进优化法以及水平集方法等主要优化设计方法。

变密度法[6]不需要引入真实的材料微结构和附加均匀化求解，程序实现简单，优化效率高，因此得到了广泛的应用。利用Hyperworks和ANSYS两款有限元分析软件基于变密度法对直角坐标机器人悬臂结构进行拓扑优化，重构筋肋分布，并对优化前后的结构进行了有限元对比分析[7-8]。结果表明，优化后的悬臂件强度高、重量轻、结构简单，既保证了工作性能要求又达到了轻量化设计的目的。该方法对其他连续体结构的分析及拓扑优化设计具有一定的借鉴参考意义。

1 基于变密度法的拓扑优化技术

拓扑优化是以材料分布为优化对象，将区域整体通过网格划分离散成若干有限元网格单元，在给定的目标和约束条件下，在均匀分布材料的设计空间中反复进行材料分布的计算，找到最佳的材料分布方案[9]。拓扑优化可以给定一个单一目标，其他条件作为约束，也可以给定多个目标，将这些目标给定权重后用函数关联起来组合成一个复合目标，再给定一些约束条件进行优化。由于拓扑优化手段相当灵活，所以可对设计工作提供很好的参考方向。

变密度法的基本思想是将材料密度设定成可变的，材料的其它一系列的物理参数(杨氏模量、抗拉强度、弯曲刚度等)都随材料的密度变化而发生改变。优化时以材料密度为拓扑设计变量，这样结构拓扑优化问题被转换为材料的最优分布问题[10]。建立数学模型如图1。

图1 拓扑优化数学模型

其中，xi为设计变量，代表各设计单元的相对密度，当xi=0时，表示该处材料应当去除，当xi=1时，表示此处材料需保留。C(x)代表结构的柔顺度，K为系统的总刚度矩阵，U为位移矩阵，F为外力矩阵，V为结构体积，V*为设定的体积分数上限。以体积V为约束变量，最终求得材料的最佳分布X。

2 拓扑优化设计流程

Hyperworks是一个开放的CAE平台，集成了有限元设计和分析的各种工具模块[11]。本文利用Hyperworks软件的Optistruct平台对直角坐标机器人悬臂结构进行拓扑优化。用户只需设置好模型的材料属性、载荷、约束条件，然后定义目标函数、设计变量、求解约束条件，软件便可以自动给出最优解。本文以体积最小为优化目标，以位移、应力为求解约束条件，在保证最大位移和应力满足工作性能需求的条件下得到重量最轻的悬臂结构和最优的筋肋分布。拓扑优化的具体流程如图2所示。

图2 拓扑优化流程图

3 悬臂结构多目标拓扑优化设计

3.1 直角坐标机器人三维模型建立及负载分析

该直角坐标机器人主要由底座立柱、X轴横梁、Y轴悬臂梁、Z轴导轨以及各轴的伺服运动单元组成，利用Solidworks建立三维模型如图3所示。Y轴悬臂梁总长度1500mm，材料为铝合金。机器人工作时，悬臂梁承受复杂的空间载荷，除了悬臂部件本身的自重引起的稳定变形外，Y轴的运动以及Z轴部件从导轨一端移动到其他位置时也会引起Y轴悬臂梁不稳定的弯曲变形。为提高生产效率，机器人在上下料时做高速运动，由于制造和安装误差，势必会带来冲击和振动，这些都会加剧悬臂梁的变形。

图3 直角坐标机器人三维模型

3.2 整机有限元分析

在进行有限元分析时，网格划分质量的好坏决定了最终分析结果的准确程度[12]。为了得到高质量的网格划分，本文首先对直角坐标机器人的模型进行了简化，去除了倒角、圆角、小螺纹孔等复杂特征，简化了电机和传动系统模型，保留了主要结构件(三组梁)的特征，另外在分析中省去了两根底座，而主要分析梁部分的变形情况。

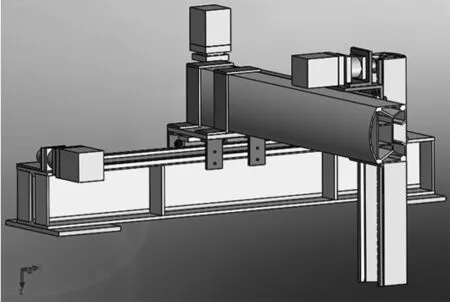
图4 直角坐标机器人简化模型

简化后直角坐标机器人模型如图4所示。将简化后的模型导入Ansys Workbench中，当X轴滑台位于横梁中间位置，Y轴滑台位于悬臂梁最远端位置时的整机受力和变形最大。因此，分析此时整机的应力和变形情况对工程实际最具指导意义。将X轴横梁两端取作固定约束，为整机施加重力，并在Z轴末端抓手处(此处已将抓手简化去除)施加200kg工作载荷，分析计算结果如图5所示。

(a)变形云图

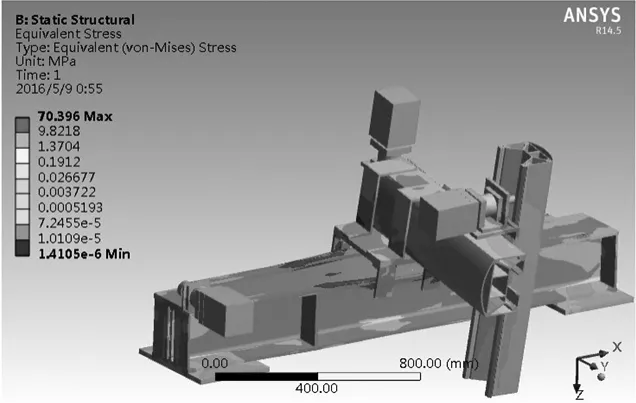
(b)应力云图图5 负载200kg时整机变形云图和应力云图

由分析结果可知，整机最大位移出现在Z轴上部及Z轴驱动电机处，最大可达1.3mm，机器人末端抓手部分的位移不超过1.1mm，基本满足普通抓取要求，定位精度还有待进一步提高；整机最大应力出现在X轴滑块处，最大为70.396MPa，存在高应力区。由此可见Y轴悬臂梁的强度、刚度等力学性能对整机的变形影响很大，若能对Y轴结构进行轻量化设计以减轻Y轴自重，提高悬臂件刚度，那么Y轴末端累计变形将会大大减小，抓取精度将会有很大提升。

3.3 悬臂结构拓扑优化

由于Y轴悬臂梁为铝型材，考虑到制造工艺，对其整体进行拓扑优化意义不大，所以只需对其横截面进行拓扑优化，得到最优的截面形状和筋肋分布，在三维绘图软件中重新建模即可得到最终结构。

首先在Solidworks中建立Y轴截面薄板的三维模型，将简化后的Y轴截面薄板三维模型导入到Hyperworks中，重新建立Y轴的有限元模型。考虑到Y轴悬臂梁与其他零件之间的装配关系，把Y轴的有限元模型划分为设计空间与非设计空间两部分：仅对设计空间进行拓扑优化设计，使材料在此空间内重新分布，从而达到在保证力学性能的同时又能减轻重量，节省材料的目的；对于非设计空间，单元形状与数目均不改变，以保证装配功能性的实现。综合考虑各种因素，确定的设计空间与非设计空间区域如图6所示，其中棕色部分为设计空间，红色部分为非设计空间。

图6 Y轴截面模型及空间划分

以增大该截面的刚度为目标函数，设定体积分数上限60% 为约束条件，设计空间内每个单元的密度为设计变量，对该模型进行拓扑优化，经过24步迭代，将密度阀值设置为0.3，求出的密度云图如图7所示，图中蓝灰色的部分为可以去除的结构。

图7 Y轴截面拓扑优化结果

从图7可以看出悬臂梁可以去掉左侧竖直筋板，截面内部上方的水平筋板，下方的“人”字形筋板也可以去除，而中间竖直筋板需要延长，以增加刚度。根据拓扑优化结果，重新对悬臂梁横截面进行建模，得到新的截面如图8b所示。优化后的截面形状更加简单，多呈封闭的三角形框架结构，主要支撑结构得到了加强，细小结构进行了合并，既能满足承载要求，又降低了加工制造的成本和难度。

(a)优化前 (b)优化后图8 优化前和优化后横截面结构对比

3.4 优化前后悬臂结构性能对比分析

根据3.3节中悬臂件横截面的拓扑优化结果，在Solidworks中建立优化后的悬臂件三维模型，将其导入到Hyperworks中生成有限元分析模型，将悬臂件一端取作固定约束，施加重力、Z轴部件传递过来的力及力矩、200kg工作载荷，通过计算得出有限元分析结果与优化前进行对比，如图9、图10所示。

将优化分析结果列入下表，由表1中的对比分析结果可知，优化后的悬臂结构最大变形由原来的1.139mm减小到了1.115mm，最大应力由40.26MPa减小到了30.59MPa，同时质量减轻了16.70%。通过拓扑优化不仅改善了原结构的力学特性，而且大大减轻了原结构的重量，降低了加工制造的成本和难度，节省原材料。

表1 Y轴优化前后目标变量参数对比

(a)变形云图 (b)应力云图图9 优化前Y轴变形云图及应力云图

(a)变形云图 (b)应力云图图10 优化后Y轴变形云图及应力云图

4 结束语

本文以悬臂式直角坐标机器人为研究对象，利用Solidworks软件建立系统的三维模型，将简化后的模型导入到Ansys Workbench中进行了整机有限元分析；采用变密度法通过有限元分析软件Hyperworks对Y轴悬臂结构进行了拓扑优化和力学性能分析。根据优化结果改进了Y轴结构，提高了悬臂梁的强度和刚度，减轻了重量，得出的主要结论如下：

(1)通过有限元分析可知悬臂件是影响悬臂式直角坐标机器人末端定位精度的关键零部件，利用拓扑优化设计出高刚度、轻量化的悬臂结构对减轻机器人本体结构重量，提高定位精度意义重大。

(2)在对梁类结构进行拓扑优化时只需取其横截面进行优化，内部筋肋多采用封闭式三角形结构，主要支撑结构应加强，密集细小结构可合并。

(3)经拓扑优化后的结构虽具有良好的力学性能，但优化过程中模型和受力经过了简化，因此只能给出设计的参考方向，并不能给出精确结果。型材优化结果可能产生非标件，增加了制造难度，可选用结构相近的标准件。

[1] 王田苗，陶永. 我国工业机器人技术现状与产业化发展战略[J]. 机械工程学报,2014,50(9):1-13.

[2] Hashimdeen S H, Miodownik M,Edirisinghe M J. The design and construction of an electrohydrodynamic Cartesian robot for the preparation of tissue engineering constructs[J]. PloS one, 2014,9(11):e112166.

[3] Hinkelmann K,Kempthorne O. Design and Analysis of Experiments, Special Designs and Applications[M]. John Wiley & Sons,2012.

[4] Ming Cong, Tao Han,Qiang Zhao. New Method of Finite Element Analysis for Headstock [C]. Proceeding of 2010 International Conference on Education Technology and Computer, 2010, 3: 418-422.

[5] Eschenauer H A,Olhoff N. Topology optimization of continuum structures: a review[J]. Applied Mechanics Reviews, 2001, 54(4):331-390.

[6] 焦洪宇，周奇才，李文军，等. 基于变密度法的周期性拓扑优化[J].机械工程学报,2013,49(13):132-138.

[7] Hughes, Thomas JR. The finite element method: linear static and dynamic finite element analysis[M]. Courier Corporation, 2012.

[8] 丛明，韩滔，赵强，等. 基于组合体的高速卧式加工中心滑架有限元分析[J].中国机械工程，2011，22(13):1527-1531.

[9] 罗震,陈立平,黄玉盈,等. 连续体结构的拓扑优化设计[J]. 力学进展,2004,34(4):463-476.

[10] Ming Cong, Tie jun Wang and Cuang si Zhang, A Study of Topology Optimization Design for the Wafer Handling Robot Arm[J]. Journal of Materials Science Forum, 2009, 626-627:471-476.

[11]蔡力钢,马仕明,赵永胜,等. 多约束状态下重载机械式主轴有限元建模及模态分析[J]. 机械工程学报,2012,48(3):165-173.

[12]Rao Singiresu S,S S Rao. Engineering optimization: theory and practice[M]. John Wiley & Sons, 2009.

(编辑 李秀敏)

Design and Analysis for Cartesian Robot Cantilever Structure

ZHU Fu-kang1, LIU Yi1, DONG Hang1, MENG Fan-jie2, CONG Ming1

(1.School of Mechanical Engineering, Dalian University of Technology, Dalian Liaoning 116024, China；2. Electrical Technology Department,Yingkou Jinchen Machinery Co., Ltd., Yingkou Liaoning 115000, China)

It presents a topology optimization method for practical engineering matters, and using this method improves the cantilever structure of Cartesian robot with some mechanical properties analysis. Finite element analysis was done on the whole machine to find out the key part that influenced the machine’s accuracy. Then, the topology optimization was made on the cross section of Y-axis cantilever, the key part, by using variable density approach. After reconstructing ribs arrangement under the optimization, a finite element analysis was made on the new model. The results show the maximum deformation of the cantilever structure reduces a lot after the optimization, that the max stress has obvious decrease, and that the weight reduces significantly. This approach can provide some helpful instructions for the mechanical structure analysis and topology optimization design.

cartesian robot; cantilever structure; finite element analysis; topology optimization

1001-2265(2017)07-0060-04

10.13462/j.cnki.mmtamt.2017.07.014

2016-10-26；

2016-11-24

辽宁省科技创新重大专项(2015106011)

朱福康(1994—)，男，山东济宁人，大连理工大学硕士研究生，研究方向为工业机器人技术与应用，(E-mail)zhufukang@mail.dlut.edu.cn;通讯作者：丛明(1963—)，男，辽宁大连人，大连理工大学教授，博士，研究方向为机器人机构学、服务机器人、工业机器人技术与应用，仿生机器人与智能控制，(E-mail)congm@dlut.edu.cn。

TH166;TG659

A