考虑沿程非均匀吸汽下SAGD产能预测模型
黄世军, 熊 浩, 马奎前, 刘 昊, 程林松, 黄成辉
(1.中国石油大学石油工程教育部重点实验室,北京 102249; 2.中海石油(中国)有限公司天津分公司,天津 300452)
考虑沿程非均匀吸汽下SAGD产能预测模型
黄世军1, 熊 浩1, 马奎前2, 刘 昊1, 程林松1, 黄成辉1
(1.中国石油大学石油工程教育部重点实验室,北京 102249; 2.中海石油(中国)有限公司天津分公司,天津 300452)
蒸汽辅助重力泄油(SAGD)相比于其他热采方法对稠油开发效果更好。目前常用的SAGD产能预测模型主要基于沿程均匀吸汽提出,矿场应用困难。针对这个问题,对SAGD沿程生产过程进行试验研究,基于试验获得沿程非均匀吸汽现象,结合达西定律、热传导定律及物质平衡方程,推导出新的SAGD产能预测模型。结果表明:三维SAGD开发物理过程比二维SAGD更加复杂;所建立的新模型在产能预测上比以往的模型更加准确;以往在二维剖面上将SAGD划分为蒸汽腔上升、蒸汽腔横向扩展及蒸汽腔下降3个阶段,但是在更加符合矿场实际的包含沿程方向的三维角度,这个阶段划分方式并不适用;蒸汽干度是影响双水平井SAGD沿程蒸汽分布的一个重要因素。
蒸汽辅助重力泄油(SAGD); 数学模型; SAGD生产过程; 非均匀吸汽; 物理模拟
全球常规油气资源发现量不断减少,为了满足石油供求,对高黏稠油的开发逐渐增加。由于高黏稠油黏度大,开发难度高,相比于常规开采方法,SAGD是一项开采特稠油及超稠油油藏较成熟的技术[1-5]。Butler假设SAGD开采过程中沿程均匀吸汽,将三维问题转化为简单的二维问题,在此基础上推导出了二维剖面的SAGD产能预测公式[6-9]。后来在二维模型的基础上根据蒸汽腔形状将SAGD开采过程划分为蒸汽腔上升、蒸汽腔横向扩展、蒸汽腔下降3个阶段[10-13]。Butler的二维SAGD产能预测模型对矿场应用较差, Ong[14]提出在SAGD生产过程中,井筒中的流动阻力会导致蒸汽沿程非均匀吸汽;Nasr[15]提出双水平井SAGD沿程压降会导致蒸汽非均匀分布;Das[16]指出SAGD生产中跟端吸汽较趾端更多;Gates[17]提出蒸汽流动分布是导致沿程蒸汽分布不均的主要原因。这些学者的研究证明了沿程非均匀吸汽在SAGD生产过程的存在性。目前尚没有考虑沿程非均匀吸汽的SAGD产能预测模型,笔者通过三维物理模拟试验对SAGD沿程吸汽进行分析,建立考虑沿程非均匀吸汽的SAGD产能预测模型,基于试验数据和加拿大矿场数据,将理论结果与数值模拟和试验结果进行对比,验证模型的正确性。
1 试验设计
1.1 相似准则
为研究相对均质地层中SAGD沿程蒸汽腔的发育,建立室内物理模型时以相似理论为指导[18-19]。受模拟条件制约,不能把所有的物理量都做到相似,根据SAGD生产的主要特征筛选关键的相似准则数。首先,热量在储层中的传递是热采过程中重要的参量,

(1)
重力作为主要的驱动力,重力和黏性力的比值也是一个重要的参数,
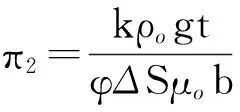
(2)
相似准则数(π1和π2)相除,重新组合可以得到
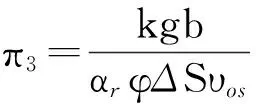
(3)
相似准则数(π1和π2)相乘,重新组合可以得到
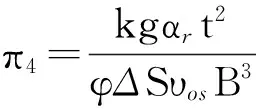
(4)
相对于其他热采方式,SAGD生产有一个特别的控制条件,即基于Subcool值的调控[20],
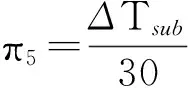
(5)
式中,λr为油藏的热传导系数,J/(m·d·℃);t为时间,d;ρr为储层的密度,kg/m3;Chpr为油藏的等压热容,J/(kg·℃);B为井距,m;k为渗透率,10-3μm2;ρo为原油密度,kg/m3;φ为储层孔隙度;ΔS为可动油饱和度;μo为原油黏度,mPa·s;αr为储层的热扩散系数,m2/s;υos为蒸汽温度下原油的运动黏度,m2/s;ΔTsub为注采井间温差,℃。
式(3)不涉及时间变量,根据π3可以设计室内物理模拟参数组合,利用加拿大麦凯河油砂区块实际储层和流体参数得到室内物理模型的参数,如表1所示。

表1 油藏参数和模型参数Table 1 Parameter values for both reservoir and physical model
1.2 物理模拟设计
双水平井组合SAGD沿程吸汽物理模拟装置由注入系统、驱替模型、加热保温系统和采集系统4大部分组成。其中,驱替模型和加热保温系统是该试验装置的主体部分,采集系统主要包括采出液收集和温度测量两部分,双水平井SAGD物理模拟如图1所示。驱替模型的内部填砂尺寸为600 mm×200 mm×50 mm(长×高×宽)。驱替模型共布置48个温度传感器,通过数据采集系统与电脑连接实现温度的实时采集、存储和显示。驱替模型外侧包裹可加热的保温套,实时调节模型温度。注入系统包括蒸汽发生器和ISCO高精度气压泵,定量/定压注入。装置的6个壁面均采用金属材料制成,耐压1.5 MPa,耐温180 ℃,且高温高压条件下密封性能良好。
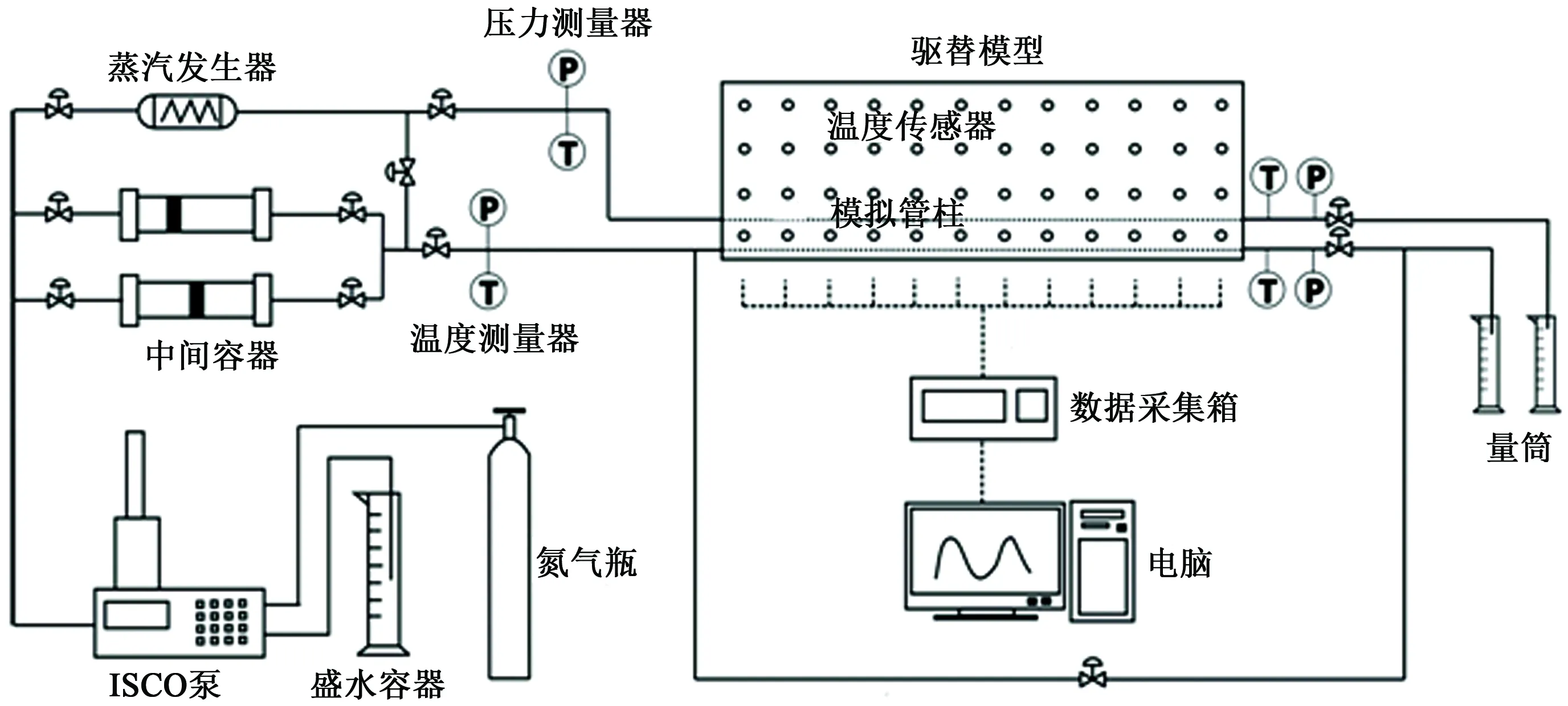
图1 双水平井SAGD物理模拟设计流程图Fig.1 Schematic diagram of physics simulation device
1.3 试验步骤
双水平井SAGD沿程吸汽物理模拟正式开始之前须进行填砂、高温气密性检测、饱和水、饱和油及恒温老化等一系列的准备工作。完整的SAGD物理模拟过程分为蒸汽循环预热阶段和SAGD正式生产阶段。

图2 蒸汽循环预热示意图Fig.2 Preheating process of SAGD
蒸汽循环预热阶段如图2所示。注汽井和生产井均为割缝的Φ6 mm管线,外侧分别用未割缝的Φ3 mm管线缠绕,蒸汽从a端注入,流经螺旋管线加热近井周围地层,由b端流出。由于预热管线未射孔,此时井筒和地层之间没有流体交换,单纯靠热传导作用传递热量。待两口井中点处温度为70~80 ℃停止预热,转入SAGD正式生产阶段。
SAGD正式生产阶段关闭循环预热管线,蒸汽从上部注汽井注入,被加热的原油和冷凝水在重力作用下流入生产井。整个模拟过程中生产井直接与大气压相连,注入蒸汽的温度维持在105~110 ℃,不断调整注汽速度,使生产井和注汽井之间的温差保持在5~40 ℃(保证既不发生汽窜,又没有过多积液);收集各个时刻的产出液,进行油水分离。同时利用温度电偶测量和记录不同时刻驱替模型内部不同点的温度,通过显示器实时显示蒸汽腔发育状态,监测蒸汽腔的发育过程。
1.4 试验结果分析
双水平井SAGD沿程温度场分布如图3所示。
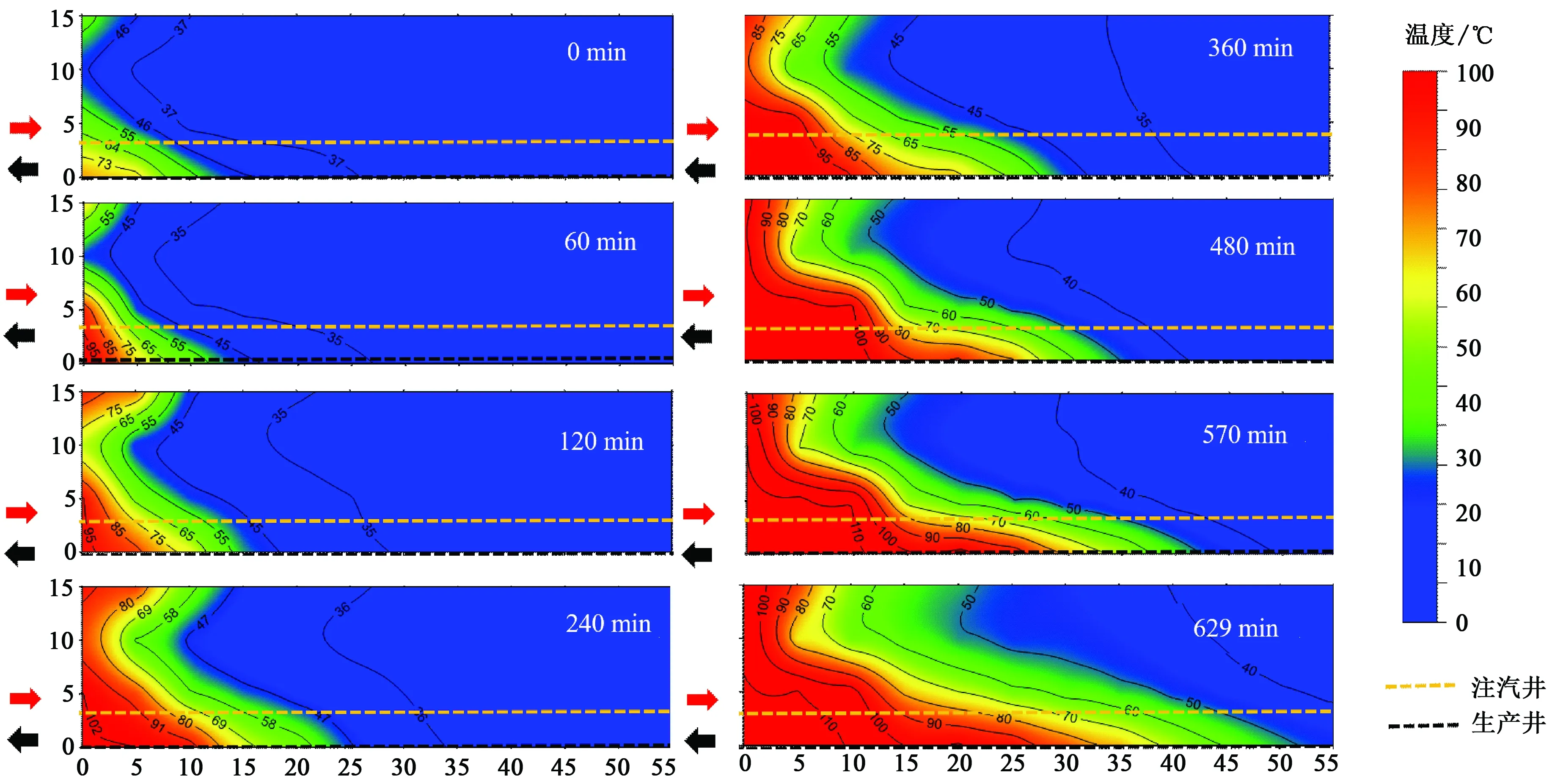
图3 双水平井SAGD沿程温度场Fig.3 Temperature distribution of dual horizontal well
由图3可见,在地层均质的情况下,跟端蒸汽腔上升较快,而趾端蒸汽腔上升慢。随着时间的不断推移,跟端蒸汽腔在360 min左右到达油层顶部,而趾端蒸汽腔上升高度依然较小;360 min后,跟端处到达油层顶部的蒸汽腔开始出现横向扩展,且跟端部位后面的蒸汽腔也相继到达油层顶部。在629 min时,蒸汽腔到达油层顶部开始出现了横向扩展,但部分蒸汽腔仍然处于上升阶段,即,双水平井SAGD沿程既有蒸汽腔横向扩展又有蒸汽腔上升阶段。由此可知在现场大部分开采过程中SAGD开采复合了两个或者三个生产阶段。
根据物理试验结果,假设沿程吸汽为凹函数递减,并将数学模型分为两部分:①跟端蒸汽腔未到达油层顶部,即此时双水平SAGD沿程都处于蒸汽腔上升阶段,模型示意图如图4(a)所示;②跟端蒸汽腔到达油层顶部,即此时双水平井SAGD沿程既有蒸汽腔横向扩展又有上升阶段,模型示意图如图4(b)所示。
假设:①蒸汽冷凝形成的水相进入油相,形成的混合物与油相具有相同的性质[21-24];②忽略高温作用下油水裂解反应产生的影响;③蒸汽腔内部等温等压;④流体渗流满足达西定律;⑤蒸汽上升过程中蒸汽腔几何形状保持相似性;⑥跟端蒸汽腔未扩展到油层边界,且蒸汽腔形状为倒三角[23]。
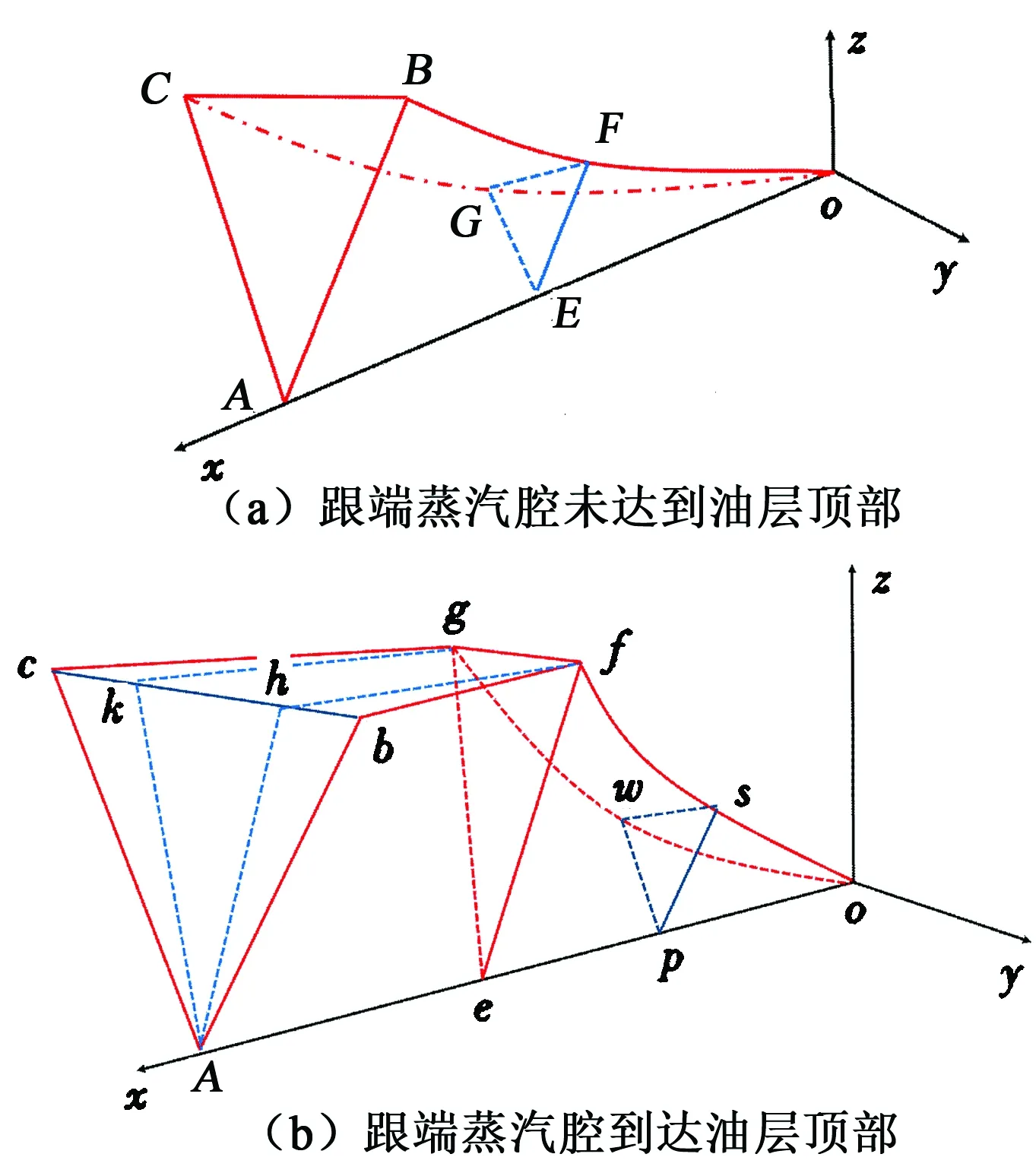
图4 数学模型示意图Fig.4 Schematic diagrams of mathematical model
2 数学模型的建立
2.1 跟端蒸汽腔未到达油层顶部
2.1.1 沿程高度函数的确定
基于假设沿程蒸汽腔呈凹函数递减模式,根据图4(a)可以得到跟端蒸汽腔未到达油层顶部时xz剖面,即沿程蒸汽腔高度分布函数,如图5所示。
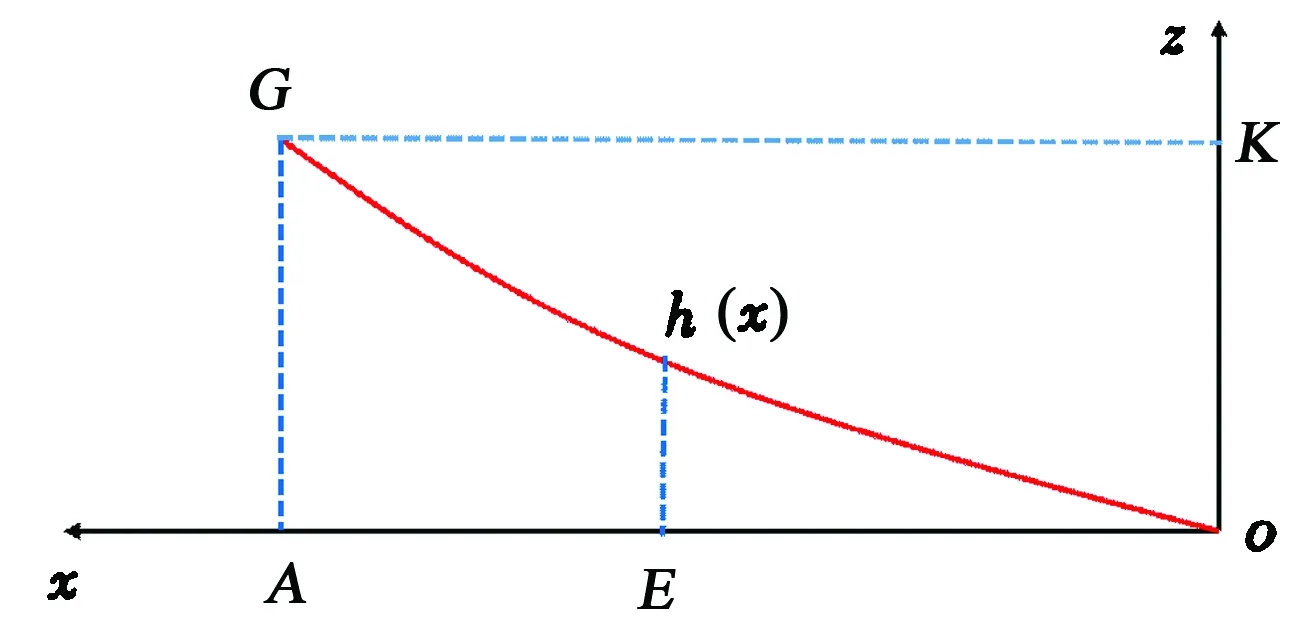
图5 跟端蒸汽腔未到达油层顶部时xz剖面沿 程蒸汽腔高度分布示意图Fig.5 Sketch map of height of steam chamber along horizontal well on xz vertical profile
由图5所示,以趾端为坐标原点,其中Ao为水平井长度,设沿程高度函数为
h(x)=a(t)xn.
(6)
式中,h(x)为蒸汽腔高度,m;a(t)为时间t的函数;n为实际沿程高度函数拟合确定的指数。
Bulter[24]推导出的斜面泄油速度方程为
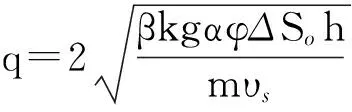
(7)
式中,q为单位长度上斜面泄油速度,m/d;β为常数,由蒸汽腔形状决定;α为油层扩散系数,m2/d;ΔSo为含油饱和度变化值;h为蒸汽腔高度,m;m为黏温常数;υs为蒸汽温度下原油运动黏度,m2/d。
假定蒸汽腔上升过程中保持形状上的相似,因此累积产油量与单位面积的可动油和蒸汽腔高度平方的乘积成正比,即
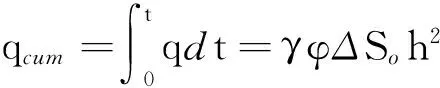
(8)
式中,γ为常数,由蒸汽腔的形状确定。
联合式(7)和(8)可以求出蒸汽腔高度h和时间t的函数关系,
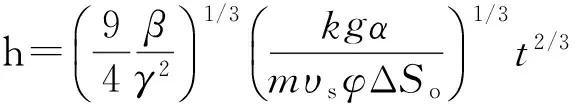
(9)
由于Butler研究的是双水平SAGD沿程均匀吸汽,因此沿程任意位置上蒸汽腔高度h和时间t的函数关系都和式(9)相同。如图5所示,其中GK为Butler所研究沿程蒸汽腔高度,AG处蒸汽腔高度h和时间t的关系可以由(11)获得,于是可以求出G点坐标为(xA,h)。
将G点坐标带入式(6)中,求得a(t)为
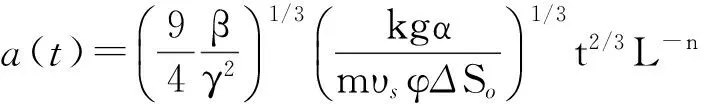
(10)
式中,L为水平井长度,m。
将式(10)带入到式(6)求解得沿程蒸汽腔高度函数为
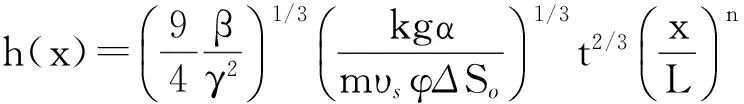
(11)
式(11)为考虑了沿程非均匀吸汽情况下,沿程水平井任意位置处蒸汽腔高度h(x)和时间t的函数关系式。
2.1.2 上产阶段产能预测模型
由式(8)可同理求出任意垂直剖面EFG的累积产能为
qcum=γφΔSoh(x)2.
(12)
对式(12)沿程进行积分,求出考虑非均匀吸汽模式下上产阶段产能预测模型,即跟端蒸汽腔未到达油层顶部时的产能预测模型(Ⅰ)为
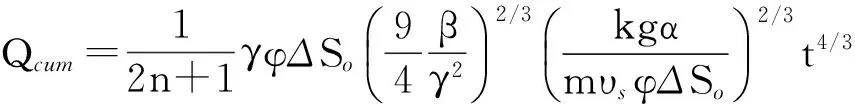
(13)
2.2 跟端蒸汽腔到达油层顶部
设跟端蒸汽腔到达油层顶部的时间为t1,当t
由图4(b)所示,e点为水平井长度Ao段上的任意点,设e点坐标为(x,0),对应时间为t,在时间t内垂直剖面egf刚好到达油层顶部。将该模型再细分为两部分:Ae段蒸汽腔全部到达油层顶部且出现横向扩展;eo段蒸汽腔都处于上升阶段。图6为跟端蒸汽腔到达油层顶部后zx剖面上沿程蒸汽腔高度分布示意图。

图6 跟端蒸汽腔到达油层顶部后xz剖面沿 程蒸汽腔高度分布示意图Fig.6 Sketch map of height of steam chamber along horizontal well on xz vertical profile
因为eo段均处于蒸汽腔上升阶段,则可以应用式(13)求取该阶段产能,即
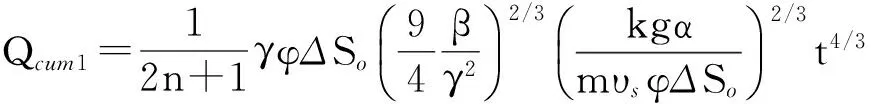
(14)
式(14)即为eo段产能预测模型。
2.2.1 Ae段产能预测模型
如图4(b)所示,垂直剖面egf沿eA方向平移到剖面Ahk,hf和gk为平移轨迹,得到三棱柱Aefgkh,该三棱柱的体积为
V1=γd2(L-x).
(15)
式中,d为油藏厚度,m。
因为多面体Aefhb和Aegck体积相等,求其中一个即可。基于Butler推导出的横向扩展长度与时间t的关系式[24],跟端a处蒸汽腔到达油层顶部的时间为t1,hb段扩展时间为(t-t1),因此可以求出hb段长度为
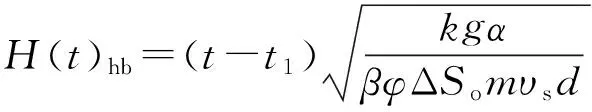
(16)
式中,H(t)为时间t内横向扩展的距离,m。
由式(11)可知,当蒸汽腔高度h(x)等于油藏厚度d时,可以得到Ae段沿程x与到达油层顶部时间t的函数关系,
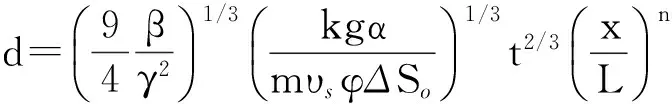
(17)
t1为跟端a处蒸汽腔到达油层顶部的时间,可由式(17)求得
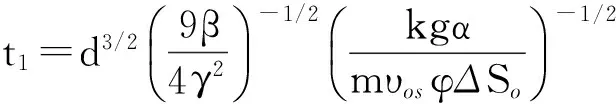
(18)
联立式(16)~(18)可求解面积Abh,
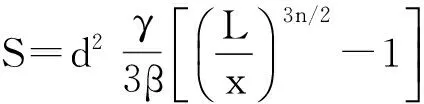
(19)
对S进行积分求得多面体Aefhb体积为
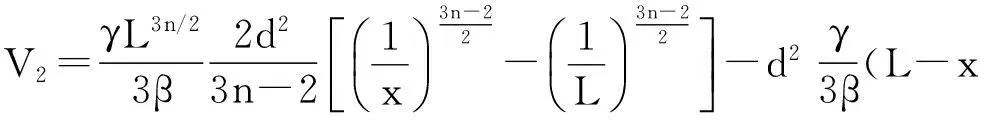
(20)
结合式(15)和(20)求得Ae段蒸汽腔的总体积为
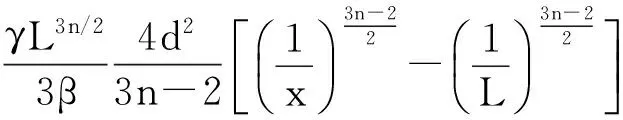
(21)
然后可以求出Ae段的累积产油量为
Qcum2=φΔSoγd2×
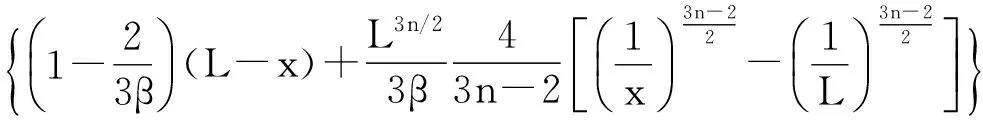
(22)
将式(17)带入(22)中,可以得到
Qcum2~t.
(23)
式(23)即为ae段产能预测模型。
2.2.2 跟端蒸汽腔到达油层顶部后产能预测模型
沿程Ao段的产能预测模型(Ⅱ)为eo段产能预测模型加上Ae段产能预测模型,即
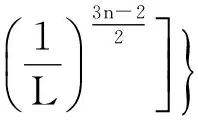
(24)
其中
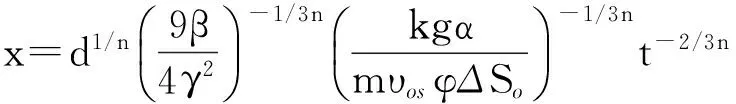
式(24)即为跟端蒸汽腔到达油层顶部后产能预测模型,且式(24)中当x=L时和式(14)相等,即e点在跟端A处,此时沿程蒸汽腔都处于上升阶段。
3 结果分析
3.1 模型验证
(1)理论模型与CMG结果对比。为了研究均质地层条件下双水平井SAGD沿程蒸汽分布情况,以加拿大Mackay River和 Dover区块的SAGD先导试验区为例,基于单个双水平井井组的地质参数,利用热采模拟软件CMG-STARS建立网格数为160×1 000×80的双水平井SAGD模型,每个网格尺寸为0.5 m×0.5 m×0.5 m,地质模型尺寸为80 m×500 m×40 m。图7为地质模型中某一垂向剖面。模型中没有底水及气顶的存在,注汽井位于生产井上面5 m,注采井长度同为400 m。油藏初始温度和压力分别为18 ℃和2 350 kPa,初始含油饱和度为0.83,初始含水饱和度为0.17,水平渗透率和垂向渗透率分别为3 400×10-3和200×10-3μm2,地层孔隙度为0.36,黏温指数为3.616,热扩散系数为0.08 m2/d,原油密度为0.98 g/cm3,生产一段时候后,残余油饱和度为0.23。相渗曲线和黏温曲线如图8所示。

图7 地质模型中某一垂向剖面Fig.7 Cross-sectional view of grid indicating depth of layers in model
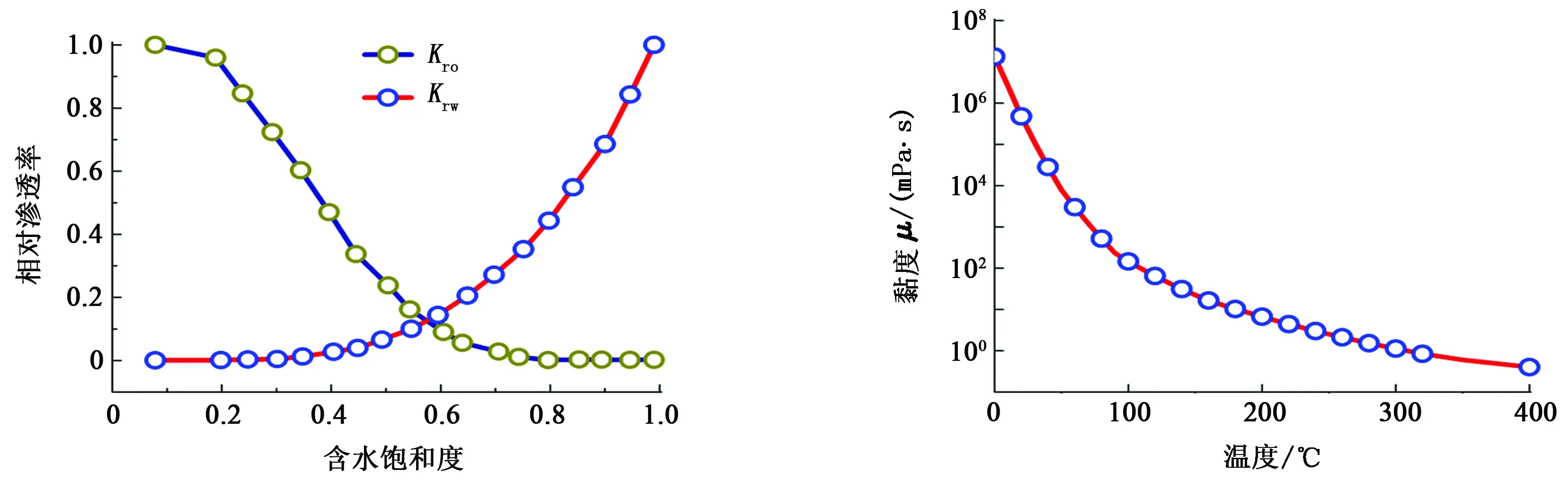
图8 相渗曲线和黏温曲线Fig.8 Real-permeability and viscosity-temperature curves for CMG simulation
应用式(11)可求出跟端蒸汽腔到达油层顶部的理论时间t1≈298 d。CMG STARS中跟端蒸汽腔到达油层顶部的时间为290 d,与理论计算时间比较符合,数模在290 d产能曲线如图9所示。
按常理参数n的拟合应用沿程蒸汽腔高度确定,但由于系数a(t)是时间的函数,这样拟合比较复杂,本文中采用拟合累积产油量的方法确定参数n。因为蒸汽腔高度函数h(x)在产能预测模型Ⅰ和产能预测模型Ⅱ均相同,但产能预测模型Ⅰ相对于模型Ⅱ简单,因此采用产能预测模型Ⅰ拟合CMG中的产能,确定参数n,拟合曲线如图10所示。
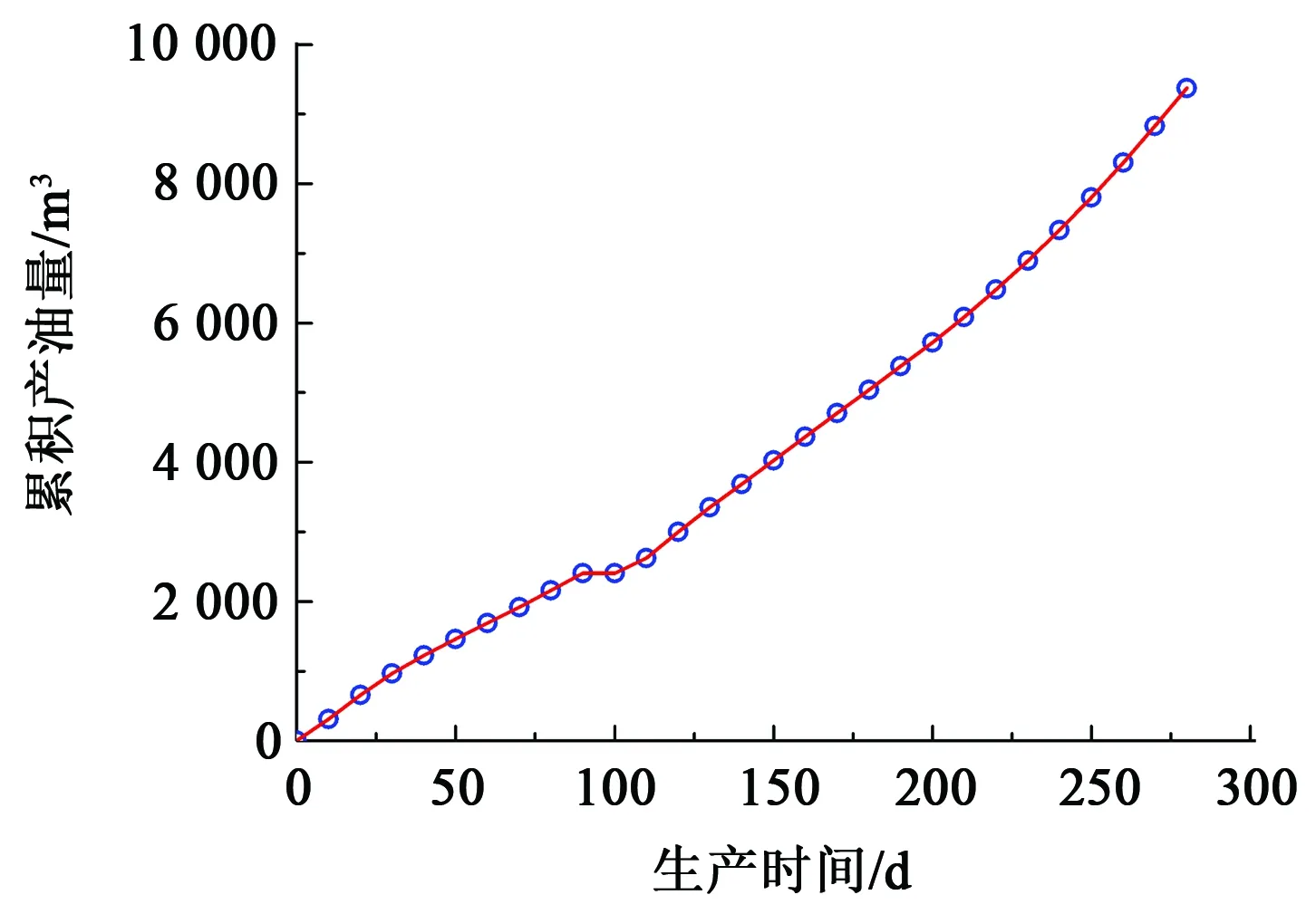
图9 CMG模型中累积产油量与时间的关系Fig.9 Relationship between cumulative oil and time in CMG model
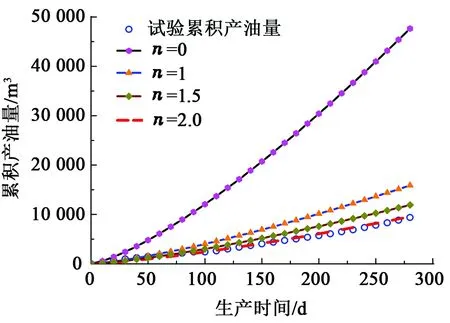
图10 不同参数n与CMG数据的拟合曲线Fig.10 Fitting curves of different numbers n and cumulative oil in CMG
由图10可见,当n=0时,即为Butler的沿程均匀吸汽预测模型,该产能预测值比实际预测值高出了许多;当n=1,即沿程蒸汽腔高度呈均匀递减时,预测结果也比CMG结果高出许多;最后拟合当n=2时,其结果与CMG结果拟合较好。
在确定参数n=2的条件下,用产能预测模型II对双水平井SAGD跟端蒸汽腔到达油层顶部后产能进行预测,结果如图11所示。
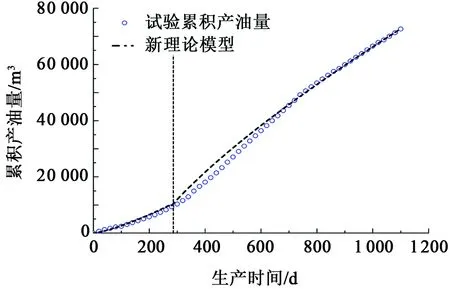
图11 理论模型与CMG模型拟合曲线Fig.11 Fitting curves of mathematical model and CMG model
由图11所示,当n=2时,虚线右侧为跟端蒸汽腔到达油层顶部后的模型与CMG的拟合曲线,拟合较好,证明了该理论模型的正确性。
(2)理论模型与试验结果对比。试验结果中:含油饱和度变化值ΔSo为0.7,蒸汽温度下的原油运动黏度为0.25 m2/d,热扩散系数为0.021 m2/d,再结合表1中的试验参数,可以得到理论模型的输入参数。
应用前文所述方法可以得出:当参数n为2.5时,产能预测模型Ⅰ与试验第一阶段累积产油量拟合效果最好,如图12所示。然后再用产能预测模型Ⅱ预测之后的试验数据,预测结果如图13所示。从图13中可以看出,产能预测模型与试验数据拟合效果较好,但是在生产时间到达450 min后,产能预测模型预测的结果高于试验数据,这主要是由于450 min后试验中发生了剧烈的汽窜现象。
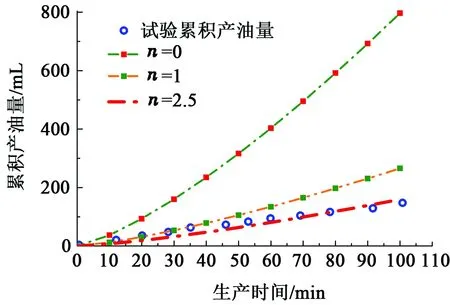
图12 物理模拟试验中不同参数n与CMG 数据的拟合曲线Fig.12 Fitting curves of different numbers n of cumulative oil production in experimental data
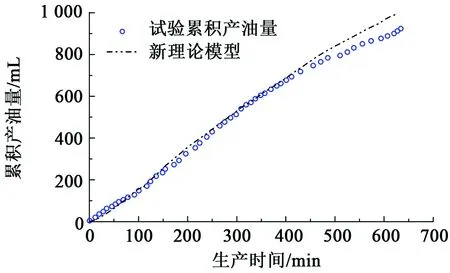
图13 试验数据与理论模型拟合曲线Fig.13 Fitting curves of mathematical model and experimental data
3.2 参数n的影响
产能预测模型中,参数n是一个重要参数,它由沿程蒸汽腔分布决定。分别对孔隙度、渗透率、蒸汽温度、注采压差、注采速率及蒸汽干度进行研究,结果如图14和15所示。结果表明:蒸汽干度对沿程蒸汽分布影响显著。随着蒸汽干度的增加,沿程蒸汽分布逐渐趋于均匀。蒸汽干度在沿程方向上不断降低,跟端蒸汽上升量远远大于趾端,导致跟端吸汽量大于趾端;同时因为跟端吸汽量更大,更多的受热稠油流向生产井,这样也就需更多的蒸汽填补其空间,使更多的蒸汽注入跟端,最后导致沿程非均匀吸汽加重。

图14 不同蒸汽干度下的沿程蒸汽分布Fig.14 Steam distribution along horizontal well in CMG STARS at different steam quality
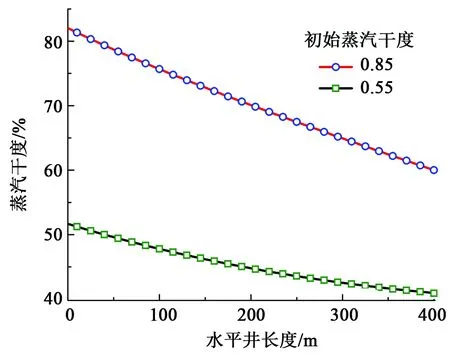
图15 水平井沿程蒸汽干度变化Fig.15 Steam quality distribution along horizontal direction
4 结 论
(1)双水平井SAGD沿程物理过程为跟端蒸汽腔首先到达油层顶部,趾端蒸汽腔到达油层顶部时间较长,跟端蒸汽腔到达油层顶部后开始出现横向扩展时,趾端蒸汽腔仍然处于上升阶段,即在某一时刻,沿程蒸汽腔既有横向扩展又有上升阶段。
(2)针对该物理过程,建立了相对应的数学模型,通过该数学模型与数值模拟和试验结果对比,证明该数学模型准确度较高,并且相比于数模具有更高的计算速度,便于现场的快速预测。
(3)沿水平井方向,蒸汽干度的降低也是影响双水平井SAGD沿程蒸汽分布不均的一个重要因素。
[1] 杨立强, 陈月明,王宏远,等.超稠油直井-水平井组合蒸汽辅助重力泄油物理和数值模拟[J].中国石油大学学报(自然科学版),2007,31(4):64-69. YANG Liqiang, CHEN Yueming, WANG Hongyuan, et al. Physical and numerical simulation of steam assisted gravity drainage with vertical and horizontal well combination in extra heavy oil reservoir[J]. Journal of China University of Petroleum(Edition of Natural Science), 2007,31(4):64-69.
[2] 鹿腾,李兆敏,孙晓娜,等.泡沫辅助SAGD开发特征[J].中国石油大学学报(自然科学版),2014,38(3):93-98. LU Teng, LI Zhaomin, SUN Xiaona, et al. Characterization of foam assisted SAGD process[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014,38(3):93-98.
[3] 高永荣,刘尚奇,沈德煌,等.氮气辅助SAGD开采技术优化研究[J].石油学报,2009,30(5):717-721. GAO Yongrong, LIU Shangqi, SHEN Dehuang, et al. Optimization of N2injection technology during steam assisted gravity drainage process[J]. Acta Petrolei Sinica,2009,30(5):717-721.
[4] 马德胜,郭嘉,昝成,等.蒸汽辅助重力泄油改善汽腔发育均匀性物理模拟[J].石油勘探与开发, 2013,40(2):188-193. MA Desheng, GUO Jia, ZAN Cheng, et al. Physical simulation of improving the uniformity of steam chamber growth in the steam assisted gravity drainage[J].Petroleum Exploration and Development, 2013,40(2):188-193.
[5] 林日亿,李魏,李兆敏,等.烟气-蒸汽辅助重力泄油模拟技术[J].中国石油大学学报(自然科学版),2012,36(5):136-140. LIN Riyi, LI Wei, LI Zhaomin, et al. Numerical simulation technology of flue gas-steam assisted gravity drainage[J]. Journal of China University of Petroleum(Edition of Natural Science), 2012,36(5):136-140.
[6] BUTLER R M, STEPHENS D J. The gravity drainage of steam-heated heavy oil to parallel horizontal wells[J]. Journal of Canadian Petroleum Technology, 1981,20(2):90-96.
[7] BUTLERR M. SAGD comes of AGE![J]. Journal of Canadian Petroleum Technology, 1998,37(7):9-12.
[8] BUTLER R M, MCNAB G S, LO H Y. Theoretical studies on the gravity drainage of heavy oil during in-situ steam heating[J]. Canadian Journal of Chemical Engineering, 1981,59(4):455-460.
[9] BUTLER R M. A new approach to the modelling of steam-assisted gravity drainage[J]. Journal of Canadian Petroleum Technology, 1985,24(3):42-51.
[10] 刘志波,程林松,纪佑军,等.蒸汽与天然气驱(SAGP)开采特征:与蒸汽辅助重力泄油(SAGD)对比分析[J].石油勘探与开发,2011,38(1):79-83. LIU Zhibo, CHENG Linsong, JI Youjun, et al. Production features of steam and gas push: comparative analysis with steam assisted gravity drainage [J]. Petroleum Exploration and Development, 2011,38(1):79-83.
[11] SABETI M, RAHIMBAKHSH A, MOHAMMADI A H. Using exponential geometry for estimating oil production in the SAGD process[J]. Journal of Petroleum Science & Engineering, 2015,138:113-121.
[12] WEI S, CHENG L, HUANG W, et al. Prediction for s- team chamber development and production performance in SAGD process[J]. Journal of Natural Gas Science & Engineering, 2014,19(7):303-310.
[13] SUN X G, WAN-JUNA H E, XIAO-BOB H U, et al. Parameters optimization of different production stages by dual-horizontal well SAGD process for super-heavy oil reservoir[J]. Xinjiang Petroleum Geology, 2012,33(6):697-699.
[14] ONG T S, BUTLER R M. Wellbore flow resistance in steam-assisted gravity drainage[J]. Journal of Canadian Petroleum Technology, 1990,29(6):49-55.
[15] LAW D, GOLBECK H, NASR T, et al. Counter-current aspect of the SAGD process[J]. Journal of Canadian Petroleum Technology, 2000,39(39):41-47.
[16] DAS S K. Well bore hydraulics in a SAGD well pair[R]. SPE 97922-MS,2005.
[17] WEI W, GATES I D. On the relationship between completion design, reservoir characteristics, and steam conformance achieved in steam-based recovery processes such as SAGD[R]. SPE 129694-MS,2010.
[18] HUANG S, XIONG H, WEI S, et al. Physical simulation of the interlayer effect on SAGD production in mackay river oil sands[J]. Fuel, 2016,183:373-385.
[19] 史琳,员盼锋,昝成,等.注蒸汽采油高压模型水平井相似准则及模化[J].中国石油大学学报(自然科学版),2012,36(1):136-140. SHI Lin, YUAN Panfeng, ZAN Cheng, et al. Similarity criterion on steam recovery high pressure model horizontal well and modeling[J]. Journal of China University of Petroleum(Edition of Natural Science), 2012,36(1):136-140.
[20] STONE T W, BROWN G, GUYAGULER B, et al. Practical control of SAGD wells with dual-tubing strings[J]. Journal of Canadian Petroleum Technology, 2014,53(1):32-47.
[21] YANG Y, HUANG S, LIU Y, et al. A multistage theoretical model to characterize the liquid level during steam-assisted-gravity-drainage process[R]. SPE-183630-PA, 2016.
[22] IRANI M, GATES I D. Understanding the convection heat-transfer mechanism in steam-assisted-gravity-drainage process[J]. SPE Journal, 2013,18(6):1202-1215.
[23] REIS J C. A steam assisted gravity drainage model for tar sands: radial geometry[J]. Journal of Canadian Petroleum Technology, 1993,32(8):43-48.
[24] BUTLER R M. Thermal recovery of oil and bitumen [M]. Alberta: Prentice-Hall, 1991.
(编辑 李志芬)
A mathematical model for productivity prediction of SAGD process considering non-uniform steam distribution
HUANG Shijun1, XIONG Hao1, MA Kuiqian2, LIU Hao1, CHENG Linsong1, HUANG Chenghui1
(1.MOEKeyLaboratoryofPetroleumEngineeringinChinaUniversityofPetroleum,Beijing102249,China;2.TianjinBranchofCNOOCLimited,Tianjin300452,China)
Steam-assisted gravity drainage (SAGD) process has many advantages over other thermal recovery methods for bitumen recovery. The current models used for productivity prediction of the SAGD process have been found not adequate for field application since the effects of steam nonconformance along the well were not considered. In this study, dedicated laboratory experiments were conducted to investigate the sectional recovery along the horizontal well during simulated SAGD process. A new mathematical model considering non-uniform steam distribution was established based on the experimental results and combining the Darcys law and heat transfer as well as mass balance models in the SAGD process. The results indicate that the real 3D SAGD recovery process along the horizontal well is more complex than that described in a single 2D vertical profile, and the newly proposed model is more accurate in productivity prediction than the previous models. The previous descriptions of the steam distribution in a 2D profile (i.e. the rising steam chamber, the lateral expansion of the steam chamber when it reaches cap-rock, and the declining steam chamber when it reaches the boundary) are not applicable for the whole horizontal well section. Moreover, steam quality is an important factor that can influence the steam distribution along the horizontal well.Keywords: steam assisted gravity drainage (SAGD); mathematical model; SAGD recovery process; non-uniform steam distribution; physical simulation
2016-09-27
“十三五”国家重大科技专项(2016ZX05031-003-005)
黄世军(1974 -),男,副教授,博士,研究方向为稠油热采、油气渗流理论和复杂结构井开发。E-mail:Fengyun7407@163.com。
1673-5005(2017)04-0107-09
10.3969/j.issn.1673-5005.2017.04.014
TE 357.44
A
黄世军,熊浩,马奎前,等.考虑沿程非均匀吸汽下SAGD产能预测模型[J].中国石油大学学报(自然科学版),2017,41(4):107-115.
HUANG Shijun, XIONG Hao, MA Kuiqian, et al. A mathematical model for productivity prediction of SAGD process considering non-uniform steam distribution[J].Journal of China University of Petroleum(Edition of Natural Science),2017,41(4):107-115.

