横观各向同性地基上的碾压混凝土重力坝应力应变研究
苏超+董安雨+刘崇巍+何志亮+徐汇


摘要:碾压混凝土重力坝结构简单,施工方便,应用广泛。在实际工程中,经常会遇到地基的各向异性问题。应用非线性有限元结构分析软件ABAQUS,以某碾压混凝土重力坝的岸坡坝块为研究对象,建立了碾压重力坝的三维有限元计算模型。在正常蓄水工况下设置了六组水平向与铅直向弹性模量比值不同的计算组,通过对比分析,研究其可不考虑各向异性的材料比值区间。
关键词:岸坡坝段;三维有限元;横观各向同性地基;应力应变;弹性模量
中图分类号:TV642 文献标志码:A 文章编号:1672-1683(2017)04-0155-06
Abstract:RCC gravity dam has a simple structure,can be constructed conveniently,and is widely used nowadays.In practical engineering,foundation anisotropy problems are often encountered.In this paper,we used the finite element analysis software ABAQUS,took the slope dam blocks of a roller compacted concrete gravity dam as the basic computational structure,and established a 3D finite element calculation model of RCC gravity dam.Under the normal storage condition,six different calculation groups were set that have different ratios of horizontal to vertical elastic modulus.Through comparative analysis,we studied the material ratio range within which anisotropy needs not to be considered.
Key words:bank slope dam section;three-dimensional finite element;transverse isotropic foundation;stress-strain;elastic modulus
碾压混凝土重力坝结合了混凝土重力坝的高安全性与土石坝的施工高效性,是一种施工方便、安全度高的坝型[1-3]。目前在设计碾压混凝土重力坝时使用的方法与设计常态混凝土重力坝时的方法差别不大,使用的都是材料力学法[4-9]。当坝基的材料分布均匀时,材料力学法的计算结果能够较好的反映出坝体的实际受力状况,但当坝基地质条件复杂时就会产生一定误差,通常采用有限元方法进行水工设计计算[10-13]。在有限元计算中,考虑地基的分区以及地基的塑性变形较多,但考虑地基的各向异性问题的研究相对较少,在实际问题当中应该考虑这一问题的影响[14-17]。若坝段处于岸坡位置,建基面通常设计为台阶状,应力分布将更为复杂,会出现应力集中现象。本文以某碾压混凝土重力坝的岸坡坝块为研究对象,在有限元计算中考虑了地基的横观各向同性性质,设置了六组水平向与铅直向不同比值弹性模量的计算组,研究材料横观各向同性的影响,通过对比分析,探讨需要考虑各向异性的参数区间,为设计人员提供参考依据。
1 横观各向同性计算原理
对于横观各向同性问题,通过改变各向同性材料的刚度矩阵便可以解决[18-21]。在有限元计算中材料一般是各向同性材料,即在各个方向上的材料参数是相同的,这种材料在其弹性矩阵中包含弹性模量E、剪切模量G和泊松比[WTB1X]v[WT]3个参数,其弹性矩阵表达式如下:
2 计算模型
本文算例为某碾压混凝土重力壩,有限元计算坝块位于右边岸坡上,为适应斜坡坝段的侧滑趋势增加稳定性,建基面设为台阶型,见图2。坝块长22 m,最大坝高94 m,最小坝高84 m,坝底最低高程220 m,最高高程230 m,是挡水坝段。坝身主要由RCC15混凝土和RCC20混凝土浇筑碾压而成,其表面覆盖有与坝体同等级的防渗混凝土,厚度为1 m。大坝地基包含微风化层和弱风化层,其中弱风化层地基主要位于坝底前部,其横观各向同性性质较为明显。
计算模型的坐标原点位于建基面上(图2),坐标系的X轴正方向指向下游,Y轴正方向指向左岸,Z轴正方向竖直向上;建模时为了避免地基范围过小而对坝体应力产生影响,所以在坝体上、下游各延伸了两倍坝高长度,并在建基面向下也延伸两倍坝高厚度;在边界约束方面,在地基垂直于X轴的两个表面约束其X轴方向位移,在垂直于Y轴的两个表面约束其Y轴方向位移,在底面约束其三个方向上的位移;剖分网格时采用了C3D6单元和C3D8单元,具体剖分结果见图3,整个模型离散为12 688个单元和14 642个节点。
3 横观各向同性地基计算参数
坝基有4种材料分区,考虑到材料参数的差异不大,为突出讨论研究地基横观各向同性的影响,所以在计算模型中将地基设为匀质地基。以地基水平向弹性模量与法向弹性模量的比值不同分为六组进行计算(法向减小时水平向增加),最后对比各组的计算结果。六组中第六组为对照组,各组的地基材料参数及分组情况见表1。
根据设计规范的规定,计算中考虑的荷载包括:自重、静水压力、扬压力、淤沙压力和浪压力。其中混凝土的重度为24 kN/m3,静水压力取正常蓄水位时的压力。大坝在上游设置了防渗帷幕和排水孔,由于坝体是实体重力坝并且是岸坡坝段,根据设计规范渗透压力系数应取0.35,计算结果见表2。淤沙压力按规范计算,淤沙容重取为19 kN/m3。
4 结果对比分析
4.1 X轴方向位移对比
图4为第一组坝体X轴方向位移云图,各组坝体在X轴方向上的位移趋势是大致相同的,随着高度的增加X轴方向的位移在不断地增大,且最大水平位移都出现在坝顶的位置,并且随着地基法向弹性模量的增大,坝体在X轴方向上的各组最大位移值在不断地减小。
其最大位移值变化见表3。从表中可以看出,第五组与第六组的最大位移值差0.089 mm,且差值比例为4.34%,小于5%,此时地基横观各向同性性质对水平方向位移已经影响不大了。
4.2 Y轴方向位移对比
坝体在Y轴方向上的位移值较小,特别是坝底位移,其最大位移值几乎都可以忽略不计,地基横观各向同性性质对Y轴方向位移影响并不大,所以不以Y轴方向位移大小为评判标准。
4.3 Z轴方向位移对比
图5为第一组坝体Z轴方向位移云图,坝体在Z轴方向上的位移趋势大致相同,且出现最大沉降的位置大致相同。
表4为各组坝体在Z轴方向上的位移值,从表中可以看出随着地基法向弹性模量的增大,坝体的沉降在快速减小,这说明地基的法向弹性模量对坝体的沉降有很大的影响。对比第五组的数据,与对照组的沉降值差为0.042 cm,差值比例为1.89%,此时地基横观各向同性性质对沉降的影响已经很小了。
4.4 拉应力结果对比
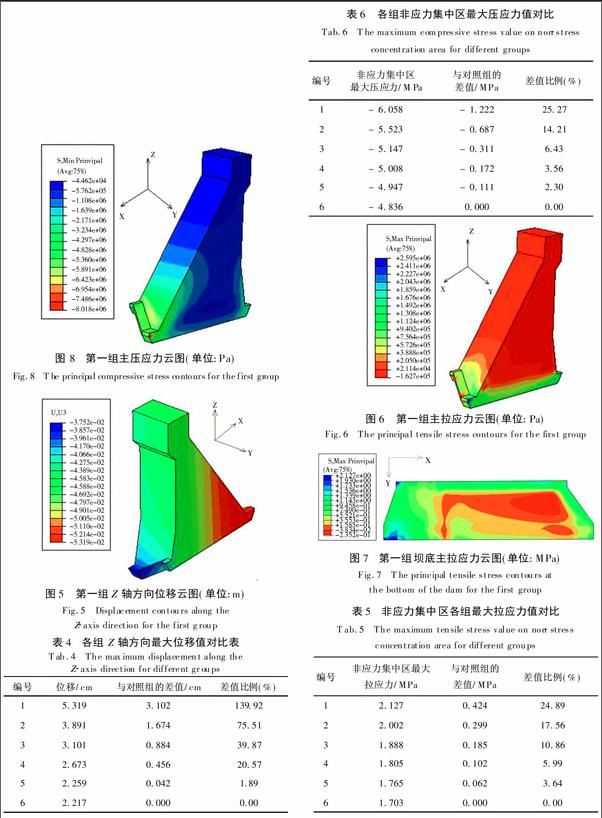
各组的拉应力分布形式大致相同,并且都在坝体220截面下游拐角处出现了拉应力集中区域(图6)。坝趾附近上部区域拉应力集中现象是由于附加区域外伸混凝土的弯曲变形所致。由于该部分结构不在常规重力坝的基本结构上,不会对重力坝整体稳定产生较大不利影响。当不考虑应力集中区时,各组坝体的最大拉应力都出现在坝体上游左侧底面,见图7。随着高度的增加拉应力在不断地减小,并且随着地基法向弹性模量的增大,壩体的拉应力值不断地减小。
4.5 压应力结果对比
图8为第一组的坝体主压应力云图,各组坝体的主压应力分布形式大致相同,并且都在坝体220截面下游拐角处出现了压应力集中区域。当不考虑应力集中区域时各组坝体的最大压应力都出现在坝体下游面底部。
表6为各组非应力集中区最大压应力值对比表。对比第五组和第六组数据可以看出二者差值不超过0.2MPa,且差值比例为2.3%,小于5%。当水平向弹性模量与法向弹性模量之比小于1.15时,地基横观各向同性对坝体压应力的影响已经很小。
5 结论
通过以上五组对比可以得到以下几个结论,一是斜坡段地基中,当地基的横向弹性模量与法向弹性模量之比小于1.15时,可以不考虑地基的各向异性性质,以各向同性匀质地基替代计算即可。二是坝体应力大小与地基的弹性模量有关,从应力对比表中可以看出,当地基的法向弹性模量增大时坝体的拉应力值和压应力值都会减小。因此在混凝土重力坝的有限元分析中,当地基的横向弹性模量和竖向弹性模量差异较大时,在计算中应当考虑地基的横观各向同性,不能再简单的将其视为各向同性体,否则计算结果将会出现较大的偏差。
参考文献(References):
[1] 程心恕,刘国明,苏言.高等水工建筑物[M].北京:中国水利水电出版社,2011.(CHENG Xin-nu,LIU Guo-ming,SU Yan.The Higher Hydraulic Structures[M].Beijing:China Water Conservancy and Hydropower Press,2011.(in Chinese))
[2] 李丽.碾压混凝土筑坝技术在世界的发展[J].中国水利.2000(10):23-24.(LI Li.The development of Roller compacted concrete damming technology in the world[J].China Hydraulic.2000(10):23-24 (in Chinese))
[3] 王松春,中国碾压混凝土筑坝技术及其发展[J].水利水电科技进展,2001(2):16-18(WANG Song-chun.Technology and Development of Roller-Compacted Concrete Dams in China[J].Advances In Science and Technology of Water Resources.2001(2):16-18)(in Chinese))DOI:10.3880/j.issn.1006-7647.2001.02.006
[4] 王海波,杨会臣,混凝土重力坝全坝段三维动力分析[J].水力发电学报,2011.30(6):133-137.(WANG Hai-bo,YANG Hui-cheng,Seismic analyses of concrete gravity dam with three-dimensional full-dam model[J].Journal of Hydroelectric Power.2011.30(6):133-137.(in Chinese))
[5] 董玉文,喻杰,苏琴.碾压混凝土重力坝碾压层厚及层面力学性能的数值分析[J].水电能源科学,2014(5):56-58.(DONG Yu-wen,YU Jie,SU Qin.Numerical Analysis of Layer Thickness of RCC Gravity Dam and Mechanical Properties of Layer Surface[J].Water Resources and Power,2014(5):56-58.(in Chinese))
[6] 魏博文,徐鎮凯,徐宝松.碾压混凝土坝层面影响带黏弹塑性流变模型[J].水利学报,2012(9):1097-1102.(WEI Bo-wen,XU Zhen-kai,XU Bao-song.Viscoelasto-plastic rheological model of effect zone for RCCD[J].Journal of Hydraulic Engineering,2012(9):1097-1102.(in Chinese))
[7] 商兆涛.碾压混凝土重力坝静力及动力特性研究[D].合肥:合肥工业大学,2009.(SHANG Zhao-tao.Roller compacted concrete gravity dam static and dynamic research[D].Hefei:Hefei University of Technology,2009.(in Chinese))
[8] 燕乔,宋志诚,张利雷,等.碾压混凝土坝碾压层厚对层间面特性影响研究[J].三峡大学学报:自然科学版.2015(01):11-13.(YAN Qiao,SONG Zhi-cheng,ZHANG Li-lei etc.Influence of RRC layer thickness on interlayer surface features[J].Three Gorges University Journal:Science and Technology.2015(01):11-13.(in Chinese))DOI:10.13393/j.cnki.issn.1672-948X.2015.01.003
[9] 刘光廷,郝巨涛.碾压混凝土拱坝坝体应力的简化计算[J].清华大学学报:自然科学版,1996(1):27-33.(LIU Guang-yan,HAO Ju-tao.Simplified numerical method in stress analysis of RCC arch dam with layered structure[J].Journal of Tsinghua University:Science and Technology,1996(1):27-33.(in Chinese))
[10] Nonlinear simulation of arch dam cracking with mixed finite element method[J].Water Science and Engineering,2008,02:88-101.
[11] 庄茁,由小川,廖剑晖,等,基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.(ZHUANG Chu,YOU Xiao-chuang,LIAO Jian-hui,et al.The finite element analysis and application based on ABAQUS[M].Beijing:Tsinghua University Press,2009.(in Chinese))
[12] 王金昌,陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006.(WANG Jin-chang,CHEN Ye-kai.The application of ABAQUS in civil engineering[M].Hangzhou:Zhejiang University Press,2006.(in Chinese))
[13] 朱向荣,王金昌.ABAQUS软件中部分土模型简介及其工程应用[J].岩土力学.2004(S2):144-148.(ZHU Xiang-rong,WANG Jing-chang.Introduction to partly soil models in ABAQUS Software and their application to the geotechnical engineering[J].Rock and Soil Mechanics.2004(S2):144-148.(in Chinese))DOI:10.3969/j.issn.1000-7598.2004.z2.029
[14] 李美蓉.复杂地质条件下多结构面对重力坝坝基稳定性的影响及处理[J].岩土力学,2014(S1):328-333.(LI Mei-rong,Impacts of multi-structural planes on gravity dam foundation stability and treatment under complex geological conditions[J].Rock and Soil Mechanics.2014(S1):328-333(in Chinese))
[15] 徐干成,李成学,刘平.各向异性和非均质地基土上浅基础的极限承载力[J].岩土工程学报.2007,29(2):164-168.(XU Gan-cheng,LI Cheng-xue,LIU Ping.Ultimate bearing capacity of shallow footing on anisotropic and nonhomogeneous clays[J].Journal of Geotechnical Engineering.2007,29(2)(in Chinese))DOI:10.3321/j.issn:1000-4548.2007.02.002
[16] 姚仰平,孔玉侠.横观各向同性土强度与破坏准则的研究[J].水利学报,2012(1):43-50.(YAO Yang-ping,KONG Yu-xia.Study on strength and failure criterion of cross-anisotropic soil[J].Journal of Hydraulic Engineering,2012(1):43-50.(in Chinese))
[17] 靳绍岩,吴嘉丞,张久长,等.各向异性地基条件下桥墩基础冲刷稳定性分析[J].四川建筑,2010,30(6):91-93.(JIN Shao-yan,WU Jia-ceng,ZHANG Jiu-chang et al.Under the condition of anisotropic foundation pier foundation scour stability analysis[J].Sichuan Architecture,2010,30(6):91-93.(in Chinese))DOI:10.3969/j.issn.1007-8983.2010.06.037
[18] 阮懷宁,沈家荫.水工建筑各向异性地基极限平衡分析[J].大连理工大学学报1993(S1):62-67.(YUAN Huai-ning,SHENG Jia-meng.Limit equilibrium analysis of anisotropic foundation in hydreoelectric engineering[J].Journal of Dalian University of Technology 1993(S1):62-67.(in Chinese))
[19] 李婕.横观各向同性地基空间问题的位移函数解法[J].岩土工程学报,2007(1):137-142.(LI Jie,Displacement function method of space problem for transversely isotropic foundation.[J].Journal of Geotechnical Engineering,2007(1):137-142.(in Chinese))DOI:10.3321/j.issn:1000-4548.2007.01.024
[20] 艾智勇,成怡冲.三维横观各向同性成层地基的传递矩阵解[J].岩土力学,2010(S2):25-30.(AI Zhi-yong,CHENG Yi-chong.Transfer matrix solutions of three-dimensional transversely isotropic multilayered soils[J].Rock and Soil Mechanics,2010(S2):25-30.(in Chinese))
[21] 艾智勇,李博.横观各向同性层状地基平面应变问题的解析层元解[J].岩土工程学报,2012(10):1787-1791(AI Zhi-yong,LI Bo.Analytical layer element solutions to plane strain problem of transversely isotropic multilayered soils[J].Journal of Geotechnical Engineering 2012(10):1787-1791 (in Chinese))

