基于图论聚类的随机子空间模态参数自动识别

郑沛娟 林迪南 宗周红 余道兴

(1东南大学土木工程学院,南京 210096)(2福建省建筑科学研究院福建省绿色建筑技术重点实验室,福州 350025)

基于图论聚类的随机子空间模态参数自动识别

郑沛娟1林迪南2宗周红1余道兴1

(1东南大学土木工程学院,南京 210096)(2福建省建筑科学研究院福建省绿色建筑技术重点实验室,福州 350025)

为提高随机子空间法模态参数识别过程中的自动化程度,减少人为干预,提出了基于图论聚类的桥梁结构模态参数自动识别方法.首先,初步剔除由于数据精度以及噪声等引起的虚假模态;其次,采用图论聚类法,对结构模态结果依次根据基于结构频率和模态保证准则(MAC)指标定义的距离进行聚类,以自动识别出结构的真实模态.随后基于灌河大桥0.5 h的加速度数据,采用所提方法实现了结构模态参数的自动识别,并通过结构的有限元模型对识别结果进行验证.最后,将所提出的方法应用到基于灌河大桥健康监测系统采集的一年加速度数据的模态参数识别过程中,表明了该方法在桥梁结构海量加速度数据的结构模态参数自动识别中是可行的.

模态参数识别;图论聚类;随机子空间法;稳定图

桥梁结构健康监测近年来得到了广泛的应用和发展,但同时也面临着在线模态参数识别与模型修正、损伤预后及安全预后等难题及挑战.由于不需要施加人工激励以及操作方便等特点,环境激励下结构模态参数识别已经被普遍采用,随机子空间法(SSI)是一种应用较为广泛的基于时域的模态识别方法,但基于SSI法的模态识别存在人工参与、运算效率低等不足,不能满足桥梁结构健康监测系统中实时模态参数识别的需求.

由于缺乏自动模态识别及相应跟踪程序,导致桥梁健康监测的海量数据难以实时分析和应用,这也成为健康监测技术发展的瓶颈之一.为提高结构模态参数识别的效率,使基于桥梁结构健康监测海量数据的模态参数自动识别成为可能,近年来,人们开始关注环境激励下的模态参数自动识别技术,如文献[1-5]将模糊聚类方法应用到模态参数自动识别中.文献[6]提出了基于子空间跟踪的时变模态参数快速辨识算法;文献[7-8]分别采用数据缩减小波和谱系聚类方法对结构模态参数进行快速识别;文献[9-11]分别以大跨度混凝土拱桥、铁拱桥和悉尼港大桥为例,基于谱系聚类分析方法进行了桥梁运行模态参数的自动识别并取得成功;文献[12]基于多层次聚类方法进行了运行模态参数自动分析.虽然在结构模态参数自动识别方面已经取得了一定的研究成果,然而在已有的模态参数自动识别过程中,仍涉及到人为因素的影响,如模糊C均值聚类法中聚类类别数以及目前应用的其他模糊聚类方法与谱系数聚类方法距离阈值需要人为进行设定.另外,现有结构模态参数识别方法在鲁棒性、计算量的控制以及参数估计可靠性等方面还有待于进一步改善.

为减少模态参数识别过程中人为因素的影响,本文以协方差驱动的随机子空间算法为基础,首先采用模态相似指数(MSI)方法、基于距离的异常点检测算法来剔除由噪声等引起的虚假模态,然后基于图论聚类方法对结构的模态结果依次根据由频率定义的距离和基于模态保证准则(MAC)指标的距离进行聚类来最终识别出结构的真实模态,从而完成模态参数的自动识别过程.随后基于采集的灌河大桥0.5 h加速度数据,使用所提方法来识别灌河大桥的结构模态参数,并利用有限元分析结果对识别结果进行验证.最后利用灌河大桥一年的加速度数据,证明了所提方法在桥梁结构海量加速度数据的模态参数自动识别过程中的可行性.

1 协方差驱动的随机子空间识别算法

协方差驱动(COV-driven)的随机子空间识别算法(SSI-COV)的基础是系统的状态空间模型[13].该算法通过分解Toeplitz矩阵获得的可观矩阵Oi来识别结构模态.基于可观矩阵Oi,系统状态矩阵A可表示为[13]

(1)

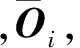
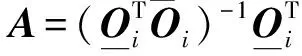
(2)

可以证明式(1)和式(2)具有相同的系统特征值[8],因此2种方法计算得到的物理模态将是完全一致的,故当式(1)与式(2)计算出来的某个模态不一致时,那么该模态一定是虚假模态.考虑到模态振型也能反映模态之间的相似性,定义改进后的模态相似指数如下[8]:

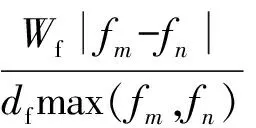
(3)

式中,Wf，Wξ，WMAC分别为频率、阻尼比、模态保证准则在计算2个模态相似系数中的权重，故三者之和为1;fm,ξm,ψm分别为通过式(1)得到的第m个模态的频率、阻尼比和振型;fn,ξn,ψn分别为通过式(2)得到的第n个模态的频率、阻尼比和振型;df,dξ,dMAC分别为频率、阻尼比、模态保证准则的容差.其中,模态保证准则是用来判断2个振型之间相关性的指标:

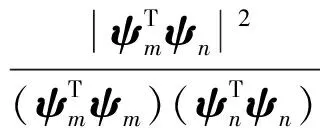
(4)

式中,MAC∈[0,1].MAC越趋于1,两者相关性越好.若频率、阻尼比、振型的差异性均大于容差,可认为2种模态完全不同,故可设定rm阈值为1.

此外,考虑到稳定图结构中虚假模态产生的稳定点较为离散,故采用基于距离的算法来实现异常点检测.

2 图论聚类方法

2.1 图论聚类方法及其流程

图论聚类方法的前提是要把聚类的数据映射为一个带权的无向图,该图是由一些节点以及连接节点之间的边所构成的几何图形[14-15].在图中,2点之间不带箭头的连线构成无向边ei,由点和无向边构成的图即为无向图,记作G=(P,E),其中,P为无向图G的点集合,E为图G的边集合.本文所涉及到的图均为无向图.本文借鉴改进的Gabire图建立数据的无向图G,其在顶点对(p,q)上的作用域定义为[14]

B(q,ad(p,q))

(5)

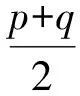
边集E的定义为

(p,q)∈E,当且仅当Γp,q∩P=∅

(6)

本文采用权值来定义2个节点之间的相似度.将无向图G中的每条边ei赋以权值w(ei),那么最小生成树(MST)是满足下列条件的生成树[16-17]:

(7)

将稳定图映射为无向图,则稳定图中的各个稳定点{v1,v2,…,vn}映射为无向图中的顶点;而稳定点之间的联系就可以映射为无向图中的边,其中每条边权值根据稳定点之间模态的差异程度确定.图论聚类方法流程如下[17]:

① 利用普里姆算法[17]在无向图G=(P,E)上构造最小生成树MST={(U,T)U=P,T={e1,e2,…,ek-1}.

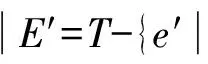
③ 获得森林F中的所有树{(Pi,Ti)i=1,2,…,q}.

④ 每棵树作为一个聚类,完成分割.

图论聚类方法是以样本数据的局域特征作为聚类的指标, 其主要优点是可将局部具有相似特征的数据进行较好地聚类.

在图论聚类方法的应用过程中,建立最小生成树后,针对2个模态之间的距离dmn所定义的阈值d对聚类结果具有至关重要的作用.2个模态之间的距离dmn类似于谱系聚类方法中2个模态之间的距离dmn.谱系聚类方法中针对2个模态之间的距离有几种不同的定义形式[8-10],这几种形式虽然大多综合考虑了频率、阻尼比、MAC以及模态能量等参数,但仅将这些参数进行简单的线性加权求和,因此它们并不能准确地反映稳定点之间真实的位置关系.另外,这些形式也不易实现合理的距离阈值的自动设定.

2.2 基于图论聚类的二次聚类法

为了克服目前谱系聚类法中2个模态之间距离定义的缺陷,本文以随机子空间模态参数识别方法为基础,提出基于图论聚类的二次聚类法对稳定图中的稳定点进行聚类来识别结构的真实模态.首次聚类时,基于图论聚类法将稳定图中频率相近的稳定点自动分类,第2次聚类时,将第1次聚类结果中每一类中振型相似的稳定点自动进行再次分类.其中第1次聚类过程中针对频率指标进行聚类所定义2个模态之间的距离为

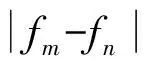
(8)

为实现对频率指标的距离阈值d的自动设定,本文基于距离矩阵,以各个稳定点之间的距离作为样本,进行概率密度函数曲线拟合.由于各个稳定轴附近会有大量距离接近的点,这些点在概率密度函数曲线上会形成多个波峰和波谷.根据该特点,本文先自动选取概率密度函数曲线上第1个波谷所对应的横坐标值,然后将此值的一半作为距离dmn的阈值.

对第1次聚类结果进行再次聚类时定义2个模态之间的MAC值的距离为

dmn-2=1-MACm,n

(9)

式中,MACm,n为第i和j个模态振型的相似度.若2个模态间的MAC值较大,表明此2个模态较为接近,此时dmn-2较小.根据实际工程经验,可以选取MAC的阈值为0.1.

经过二次聚类后,稳定图的稳定点已经根据各个稳定点之间的相似性,形成了各种规模大小不一的类.由于聚类结果中元素过少的类表示真实模态对应的稳定点所形成的类的可能性较小,故本文认为聚类结果中少于3个元素的类即为虚假模态所引起的稳定点构成的类,即各类中的元素个数的最小值Nm=3.

3 基于图论聚类的SSI模态参数自动识别

基于图论聚类的随机子空间模态参数自动识别的步骤如下:

① 采用协方差驱动的随机子空间法识别结构的模态参数,并作出稳定图.

② 采用模态相似指数方法、基于距离的异常点检测算法来剔除稳定图中由噪声等引起的虚假模态.

③ 基于图论聚类法,针对剔除虚假模态后的稳定图建立最小生成树,并根据式(8)获得第1次聚类时针对频率所定义 2个模态之间的距离.以各个稳定点之间的距离作为样本,进行概率密度函数曲线拟合,自动设定概率密度函数曲线上第1个波谷所对应的频率值的1/2为距离dmn的阈值d,进而完成基于图论聚类法的第1次聚类.

④ 根据MAC值所定义的距离作为第2个聚类指标,采用图论聚类法对第1次聚类结果进行进一步聚类.

⑤ 将聚类结果中聚类数目少于3的类进行剔除,完成模态参数自动识别.

4 实例验证

灌河大桥主桥为双塔双索面半漂浮5跨连续组合梁斜拉桥(见图1),跨径组成为(32.9+115.4+340+115.4+32.9) m.灌河大桥于2006年11月竣工通车,2013年安装了健康监测系统[18].

图1 江苏沿海高速灌河大桥

灌河大桥主桥含有11×3个加速度测点(三向),采样频率为50 Hz.本文首先采用灌河大桥0.5 h的加速度数据来识别灌河大桥的结 构 模 态参数,并采用有限元分析结果进行验证.随后基于灌河大桥一年的加速度数据,表明了所提出的方法在桥梁结构海量加速度数据的模态参数自动识别过程中的可行性.

4.1 基于有限元的灌河大桥模态分析结果

基于三阶响应面方法对灌河大桥的初始有限元模型(见图2)进行修正后,得到的各阶模态参数识别结果以及与环境振动试验相应的各阶模态结果如表1所示,修正后的有限元模型计算振型如图3所示.由表1可知,竖向频率最大相对误差不超过2%,MAC值均在90%以上.这表明修正后的有限元模型较为可靠,可为灌河大桥模态参数识别结果的验证提供参考.

图2 灌河大桥有限元模型

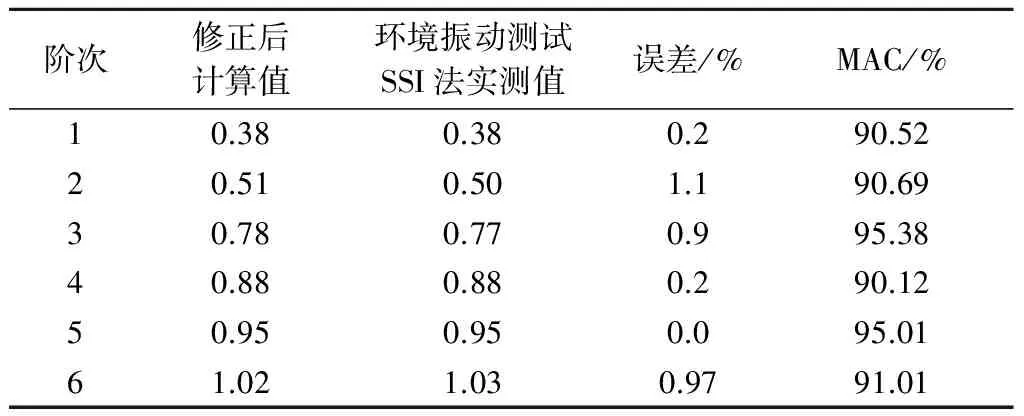
阶次修正后计算值环境振动测试SSI法实测值误差/%MAC/%10．380．380．290．5220．510．501．190．6930．780．770．995．3840．880．880．290．1250．950．950．095．0161．021．030．9791．01

(a) 1阶

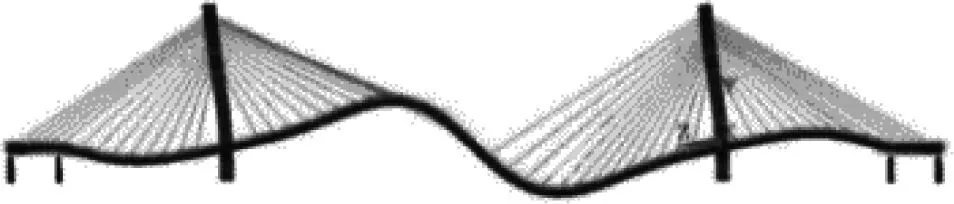
(b) 2阶

(c) 3阶

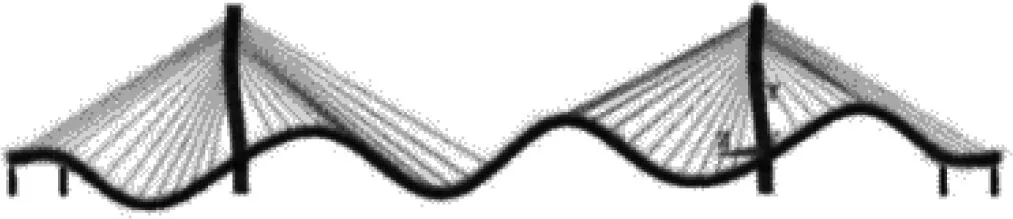
(d) 4阶

(e) 5阶

(f) 6阶

4.2 灌河大桥模态参数自动识别

本文首先基于灌河大桥健康监测系统于2014-03-27h10:46至11:16这0.5 h所采集的加速度响应数据,采用协方差驱动的随机子空间法来识别灌河大桥的结构模态参数,获得的稳定图如图4所示.针对相邻的结构模态,频率偏差临界值取2%,阻尼比偏差临界值取30%,模态振型偏差临界值取2%.

由于阻尼比的离散性较大,故在采用模态相似指数(MSI)剔除结构虚假模态的过程中,为了保留结构真实模态,将参数取值适当放大,具体取值如下:

Wf=0.5,Wξ=0.2,WMAC=0.3
df=0.15,dξ=0.2,dMAC=0.2

基于MSI剔除部分虚假模态后的稳定图如图5所示.对比图4和图5可知,部分离散虚假模态相对应的稳定点已被剔除.

采用基于距离的异常点检测算法来进一步剔除部分可能对识别结构真实模态产生干扰的稳定点,稳定图如图6所示.

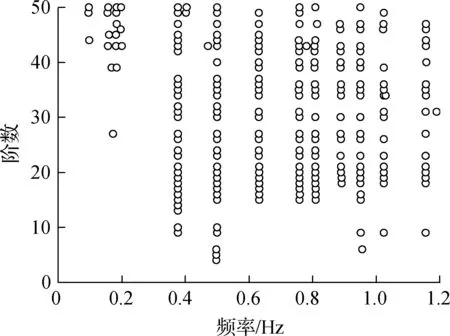
图4 采用随机子空间法获得的稳定图

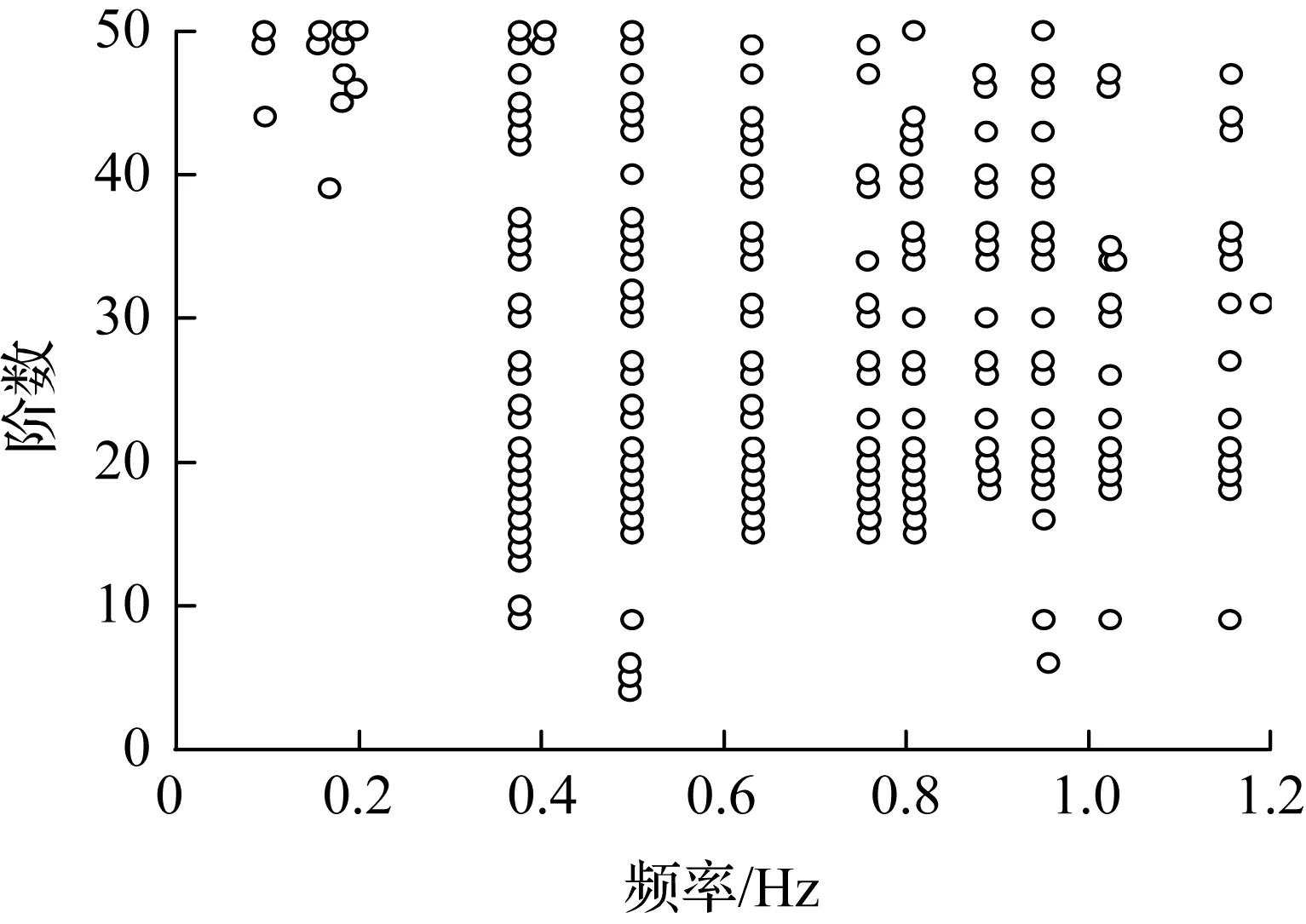
图5 基于MSI剔除部分虚假模态后的稳定图

图6 利用基于距离的异常点检测算法剔除部分 虚假模态后的稳定图

然后,以图6为基础,采用图论聚类法对稳定图中的稳定点进行聚类.具体过程如下:

① 采用普里姆算法,根据图6建立如图7所示的最小生成树,图中各稳定点表示无向图的顶点,虚线的连接表示顶点之间的边.

② 根据式(8)所定义的距离可获得图7中各阶模态间的距离,并对所得距离进行概率密度函数曲线拟合(见图8).自动选取概率密度函数曲线上第1个波谷所对应的频率横坐标的1/2作为距离dmn的阈值.采用此阈值对图7中的最小生成树进行分割,获得的第1次聚类结果如图9(a)所示,共分为10类.

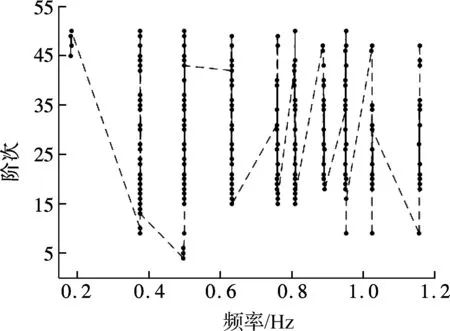
图7 基于稳定图所建立的最小生成树

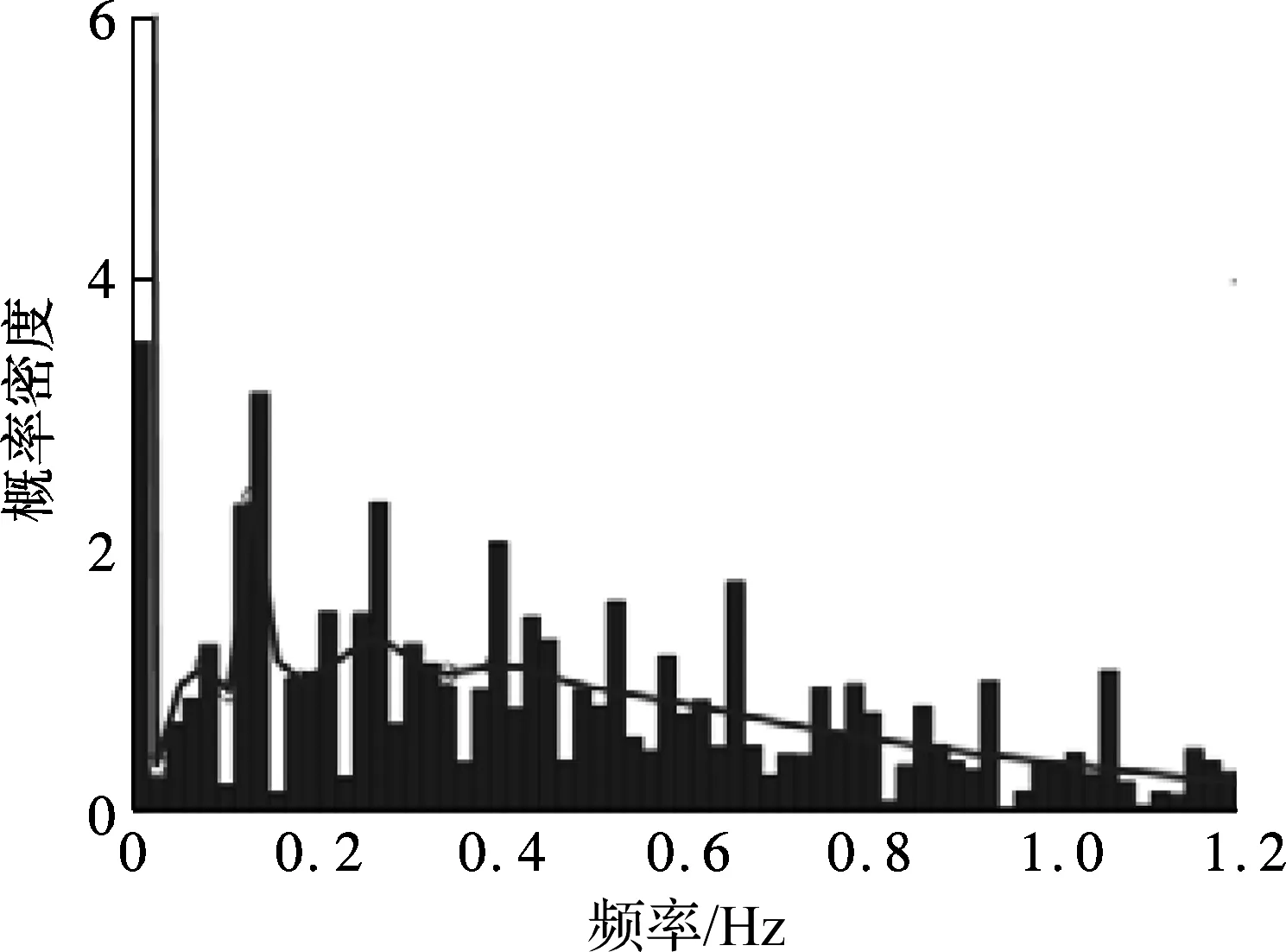
图8 拟合的概率密度函数曲线

③ 采用式(12) 定义的基于模态保证准则的距离对图9(a)的聚类结果进行进一步聚类,结果如图9(b)所示.对比图9(a)和(b)可知,2次聚类结果相同,这说明第1次聚类结果中,每个类中各个模态之间的振型十分接近.由于图9(b)的聚类结果未出现稳定点少于3个的情况,故不做剔除.

通过对比灌河大桥修正后的有限元模型获得的结构模态参数(见表1)和基于图论聚类的随机子空间模态参数自动识别的聚类结果(见图9)可知,图9中标号2,3,5,7,8,9的聚类结果分别对应灌河大桥竖向1～6阶的模态.这表明本文所提出的基于图论聚类的随机子空间模态参数自动识别方法的结果较为可靠.

最后采用上述模态参数自动识别过程,针对灌河大桥2013-10—2014-09期间采集的加速度数据来识别结构竖向前6阶模态参数.在识别过程中,基于每0.5 h所保存的数据集,进行一次结构模态参数识别,最终获得的各阶频率变化曲线如图10所示.其中,由于各个月份数据缺失情况不同,故每个月份时间跨度并不一致.另外,由于竖向4阶振型和纵向振型耦合,该阶模态不易被激励出,故识别结果所呈现的频率变化曲线连续性较差.由于灌河大桥扭转2阶和竖向3阶频率比较接近,存在干扰,故竖向3阶的识别结果较竖向1,2,5,6阶的识别效果稍差.

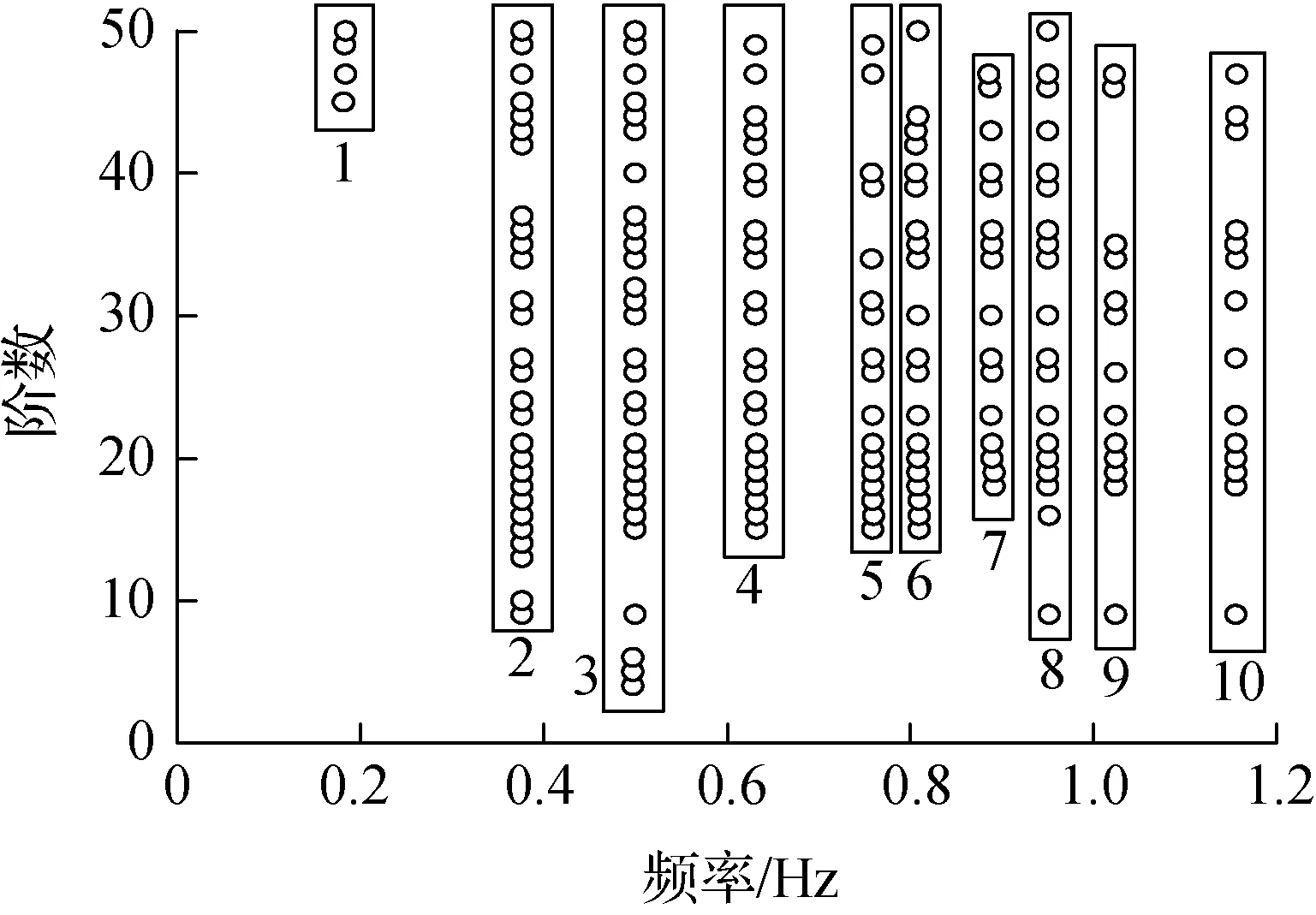
(a) 第1次聚类结果

(b) 第2次聚类结果

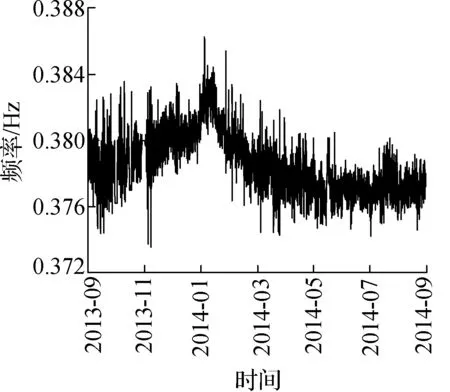
(a) 竖向1阶

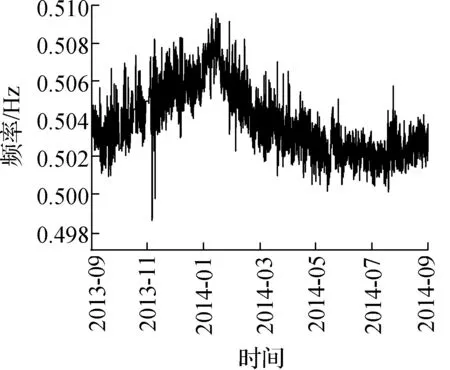
(b) 竖向2阶

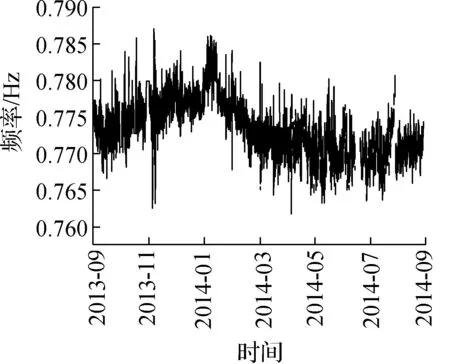
(c) 竖向3阶

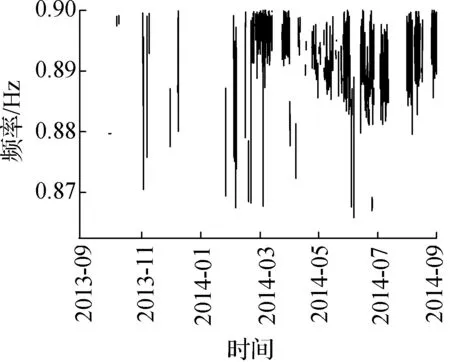
(d) 竖向4阶

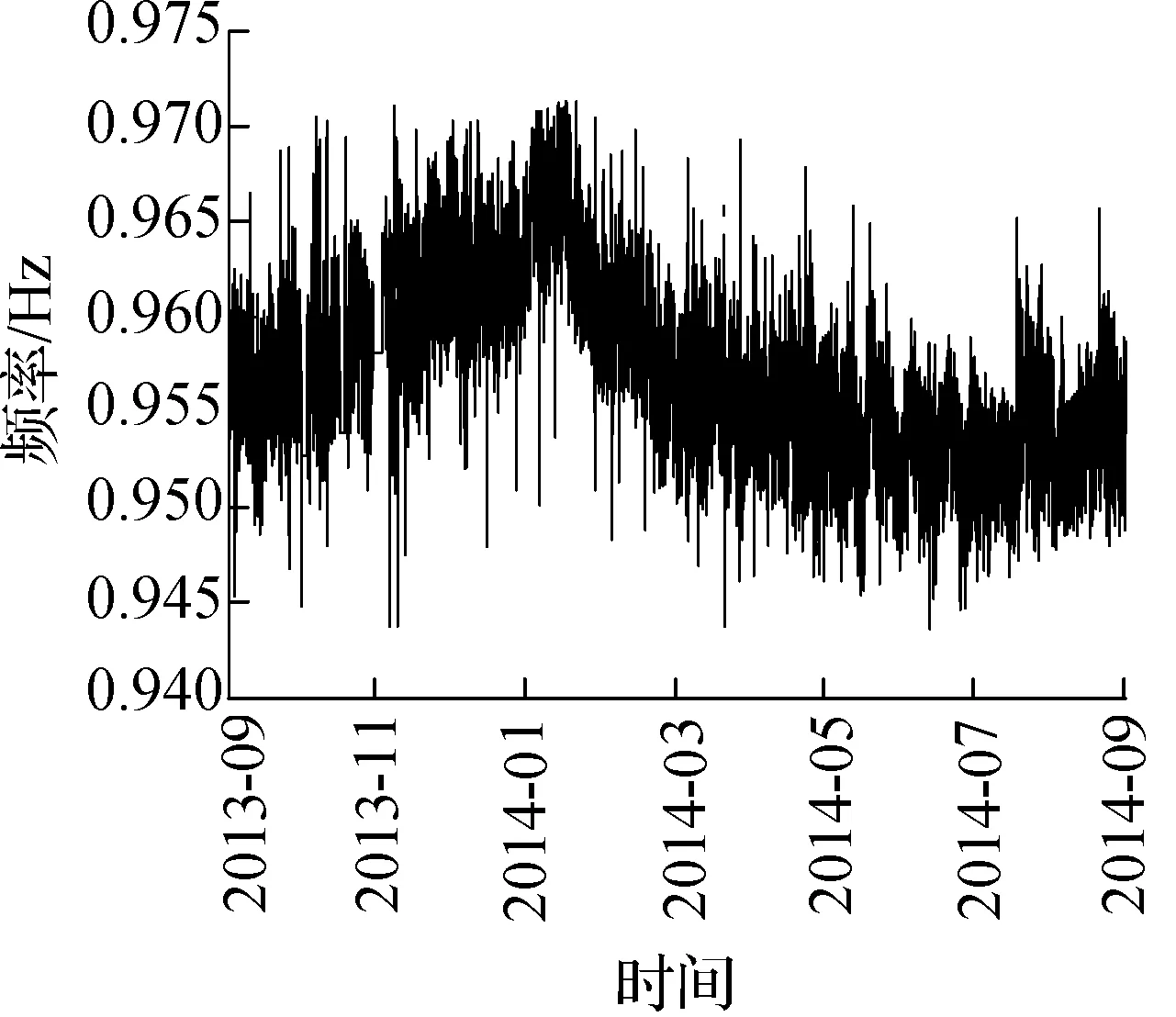
(e) 竖向5阶

(f) 竖向6阶

由图10可知,灌河大桥一年的竖向振动频率变化基本上呈正弦曲线,其中冬季的频率偏高,夏季的频率偏低,这是由于热胀冷缩的原因,与结构真实的频率响应规律相符.图10表明本文方法在针对桥梁结构海量加速度数据的模态参数自动识别中是有效的和可行的.

5 结论

1) 本文提出的基于图论聚类的随机子空间模态参数自动识别方法减少了人为因素的影响,可实现2个模态之间距离阈值的自动设定,并且聚类结果中分类较为清晰.

2) 利用采集的灌河大桥0.5 h加速度信号数据,基于所提方法可识别灌河大桥结构模态参数.识别结果与有限元分析结果对比表明,该方法的模态识别结果较为可靠.

3) 基于灌河大桥健康监测系统采集的一年加速数据,运用所提方法进行模态参数识别,结果表明该方法在针对桥梁海量加速度数据的模态参数分析过程中的可行性.

References)

[1]姜金辉, 陈国平, 张方，等. 模糊聚类法在试验模态参数识别分析中的应用[J].南京航空航天大学学报,2009,41(3):344-347. DOI:10.3969/j.issn.1005-2615.2009.03.012. Jiang Jinhui, Chen Guoping, Zhang Fang, et al. Application of fuzzy clustering theory in experimental modal parameter identification analysis[J].JournalofNanjingUniversityofAeronautics&Astronautics, 2009, 41(3): 344-347.DOI:10.3969/j.issn.1005-2615.2009.03.012.(in Chinese)

[2]孙国富. 基于模糊聚类的模态参数自动识别[J]. 振动与冲击, 2010, 29(9): 86-88. DOI:10.3969/j.issn.1000-3835.2010.09.020. Sun Guofu. Automatic modal parameters identification based on fuzzy clustering[J].JournalofVibrationandShock, 2010, 29(9): 86-88. DOI:10.3969/j.issn.1000-3835.2010.09.020.(in Chinese)

[3]Reynders E, Houbrechts J, de Roeck G. Fully automated (operational) modal analysis[J].MechanicalSystemsandSignalProcessing, 2012, 29: 228-250. DOI:10.1016/j.ymssp.2012.01.007.

[4]吴春利, 刘寒冰, 王静. 模糊聚类算法稳定图应用于桥梁结构参数识别[J]. 振动与冲击, 2013, 32(4): 121-126. DOI:10.3969/j.issn.1000-3835.2013.04.024. Wu Chunli, Liu Hanbing, Wang Jing. Parameter identification of a bridge structure based on a stabilization diagram with fuzzy clustering method[J].JournalofVibrationandShock, 2013, 32(4): 121-126. DOI:10.3969/j.issn.1000-3835.2013.04.024.(in Chinese)

[5]周思达,周小陈,刘莉,等. 基于模糊聚类的模态参数全因素自动验证方法[J].北京航空航天大学学报, 2015, 41(5):811-816. Zhou Sida, Zhou Xiaochen, Liu Li, et al. Fuzzy-clustering-based all-factor automatous validation approach of modal parameters of structures[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2015, 41(5): 811-816. (in Chinese)

[6]杨凯, 于开平, 刘荣贺，等. 两种新的基于子空间跟踪的时变模态参数快速辨识算法[J]. 工程力学,2012,29(10):294-300. Yang Kai, Yu Kaiping, Liu Ronghe, et al. Two new fast identification algorithms of time-varying modal parameters based on subspace tracking[J].EngineeringMechanics, 2012, 29(10):294-300. (in Chinese)

[7]章国稳.环境激励下结构模态参数自动识别与算法优化[D]. 重庆: 重庆大学机械工程学院, 2012.

[8]汤宝平,章国稳,陈卓. 基于谱系聚类的随机子空间模态参数自动识别[J].振动与冲击,2012,31(10): 92-96.DOI:10.3969/j.issn.1000-3835.2012.10.020. Tang Baoping, Zhang Guowen, Chen Zhuo. Automatic stochastic subspace identification of modal parameters based on hierarchical clustering method[J].JournalofVibrationandShock, 2012, 31(10): 92-96. DOI:10.3969/j.issn.1000-3835.2012.10.020.(in Chinese)

[9]Magalães F, Cunha, Caetano E. Online automatic identification of the modal parameters of a long span arch bridge[J].MechanicalSystemsandSignalProcessing, 2009, 23(2):316-329.DOI:10.1016/j.ymssp.2008.05.003.

[10]Ubertini F, Gentile C, Materazzi A L. Automated modal identification in operational conditions and its application to bridges[J].EngineeringStructures, 2013, 46: 264-278.DOI:10.1016/j.engstruct.2012.07.031.

[11]Diez A, Khoa N L D,Makki Alamdari M, et al. A clustering approach for structural health monitoring on bridges[J].JournalofCivilStructuralHealthMonitoring,2016,6(3): 429-445. DOI:10.1007/s13349-016-0160-0.

[12]Neu E, Janser F, Khatibi A A, et al. Fully automated operational modal analysis using multi-stage clustering[J].MechanicalSystemsandSignalProcessing, 2017, 84:308-323.DOI:10.1016/j.ymssp.2016.07.031.

[13]辛峻峰.基于随机子空间法的海洋平台模态参数识别技术研究[D].青岛:中国海洋大学工程学院,2013.

[14]钱云涛, 赵荣椿,谢维信.鲁棒聚类——基于图论和目标函数的方法[J].电子学报,1998, 26(2): 91-94. DOI:10.3321/j.issn:0372-2112.1998.02.021.

[15]殷剑宏,吴开亚. 图论及其算法[M].合肥:中国科学技术大学出版社, 2003: 1-4.

[16]Rosen K H. 离散数学及其应用[M]. 6版. 袁崇义,等译.北京:机械工业出版社,2011: 344.

[17]刘锁兰,王江涛,王建国，等. 一种新的基于图论聚类的分割算法[J].计算机科学,2008, 35(9): 245-247. DOI:10.3969/j.issn.1002-137X.2008.09.066. Liu Suolan, Wang Jiangtao, Wang Jianguo, et al. New segmentation technique based on clustering of graph theory[J].ComputerScience, 2008, 35(9): 245-247. DOI:10.3969/j.issn.1002-137X.2008.09.066.(in Chinese)

[18]樊星辰. 基于健康监测的结合梁斜拉桥安全预警方法研究[D].南京:东南大学土木工程学院,2014.

Automatic stochastic subspace identification of modal parameters based on graph clustering

Zheng Peijuan1Lin Dinan2Zong Zhouhong1Yu Daoxing1

(1School of Civil Engineering, Southeast University, Nanjing 210096, China) (2Fujian Key Laboratory of Green Building Technology, Fujian Academy of Building Research, Fuzhou 350025, China)

In order to improve the degree of automation in the process of modal parameter identification for bridge structures based on the stochastic subspace identification method, and reduce human intervention, an automatic modal parameter identification method based on graph clustering for bridge structure is proposed. First, some methods are adopted to initially weed out the false modes caused by the data accuracy, noise and so on. Secondly, the graph clustering theory is used to identify the structural modal parameters according to the distances defined by structural frequency and modal assurance criterion (MAC) index, respectively, so as to finish the automatic modal parameters identification. The automation modal parameters identification of the structure is realized by the proposed method based on 0.5 h acceleration data of Guanhe bridge, and the identification results are verified by the corresponding finite element model. Then, the proposed method is used to identify the modal parameters of Guanhe bridge based on one-year acceleration data from its structural health monitoring system, which indicates that the method is feasible for the modal parameter automatic identification of the bridge structure with massive acceleration data.

modal parameter identification; graph-based cluster; stochastic subspace identification method; stabilization diagram

10.3969/j.issn.1001-0505.2017.04.014

2017-01-16. 作者简介: 郑沛娟(1987—)，女，博士生；宗周红(联系人)，男，博士，教授，博士生导师，zongzh@seu.edu.cn.

国家自然科学基金资助项目(51378112)、江苏高校优势学科建设工程资助项目.

郑沛娟，林迪南,宗周红,等.基于图论聚类的随机子空间模态参数自动识别[J].东南大学学报(自然科学版),2017,47(4):710-716.

10.3969/j.issn.1001-0505.2017.04.014.

TB122,U441.3

A

1001-0505(2017)04-0710-07