无限深透水坝基悬挂式垂直防渗体保角变换-边界元渗流计算

毛海涛，王正成，王晓菊，邵东国

（1.重庆三峡学院 土木工程学院，重庆 404100；2.河海大学 环境学院，江苏 南京 210098；3.武汉大学 水利水电学院，湖北 武汉 430027）

无限深透水坝基悬挂式垂直防渗体保角变换-边界元渗流计算

毛海涛1，3，王正成1，王晓菊2，邵东国3

（1.重庆三峡学院 土木工程学院，重庆 404100；2.河海大学 环境学院，江苏 南京 210098；3.武汉大学 水利水电学院，湖北 武汉 430027）

无限深透水坝基轮廓复杂，透水层深度大，其渗流计算精度难以保证。本文提出用保角变换-边界元法计算含有无限域渗流计算问题。保角变换将复杂的坝基轮廓线边值问题变换为水平线边值问题，使渗流计算边界问题大大简化；边界元法在求解边界简单的无限域渗流方面优势明显，两种方法联合使用进行求解，能充分发挥保角变换和边界元法各自优点。通过组合法计算结果表明：联合法计算更加快捷、简单，计算结果更加符合无限域的实际情况，可为解决无限域渗流问题提供一条途径。

保角变换；边界元；无限域；渗流；坝基

1 研究背景

复变函数中的保角变换在工程中的应用多见于流体力学方面，这方面的研究也是最早的［1］。Schwarz和Christoffel给出了任意的多边形内部和上半平面之间的变换方法［2］。因此，可以将坝基复杂的地下轮廓线视为多边形，转化为简单规则的形状进行分析。对于无限域渗流区域轮廓可将其视为广义多边形，转化为水平线性进行求解［3］。边界元最早在岩土工程得到应用，其中在渗流计算中也应用广泛［4］。边界元仅仅对边界进行离散，误差只来源于边界，所以计算精度较高［5］。将保角变换后的简单渗流边界利用边界元进行离散，借助数值软件进行计算，可以使无限深透水坝基复杂的渗流计算问题得到大大简化。

因此，本研究通过选择适当的变换函数，将无限深透水坝基的复杂渗流轮廓进行保角变换，将其转换为水平线性边界，利用边界元对其进行边界离散，并借助计算机进行数值计算。提出解析与数值相结合的新方法，能较好的解决无限域的渗流问题，计算用时短且精度高。

2 模型建立

2.1 保角变换对于建立无限深透水地基上采用倒悬挂式防渗墙防渗的土石坝，其坝基的形状可以简化为图1（a）所示，复变函数中克力斯托弗-席瓦尔兹定理可将其视为广义四边形FBCD，F为无穷远点。A，E点分别是上下游坝脚所在的位置。［6］

实际计算中，假设上游坝脚A到防渗墙的距离AB=xa，下游坝脚E到防渗墙的距离ED=xe。用克力斯托弗-席瓦尔兹积分式，将实际计算Z平面四边形坝基转化到ζ平面实轴ξ上从而求解（图1（b））。转化为直线基础的公式如下：

式中：Z为Z平面上的复数，Z＝x+yi；ω为平面上的复数，ω=u+vi；a1，a2，…，an为相应多边形顶角A1，A2，A3的点经转换后在ε轴上的坐标；β1，β2，…，βn为相应于多边形的内角除以π所得值；A，B为复常数，由边界条件确定。

水平基础渗透特性复数函数公式为：

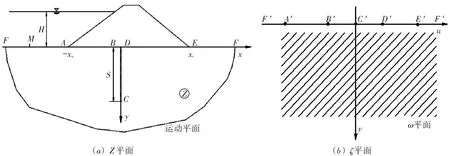
图1 渗流计算的复平面转换图

将Z=x+yi，ω=u+vi代入上式（3），分开实部和虚部得到：

2.2 边界元法由保角变换将相对复杂的坝基轮廓，转化成直线型边界，边界元在处理简单边界的问题优势明显。在描述势流的微分方程（Laplace方程），其边界条件为［7］：

其中，-u、-v为已知边界条件，在Γ1边界有B′A′F′和D′E′F′；Γ2边界有B′C′D′。将边值问题代入格林公式则有：

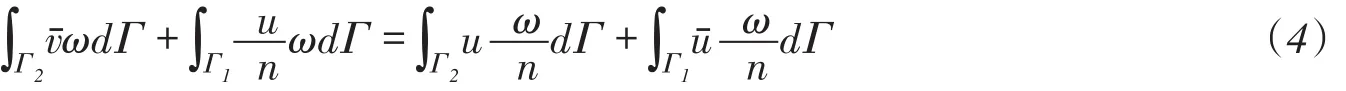
利用基本解的性质和加权余量法可将渗流的拉普拉斯方程写成如下积分式：

式中：ci为系数矩阵，为边界上点i位移向量；u，q为渗流场任意一点的位移和面力向量；u*、q*为以基本解为元素的向量［8］。

2.3 离散化对上式进行离散化，以单元节点的值ui，qi（i=1，2，…，n）代替单元上的值，则

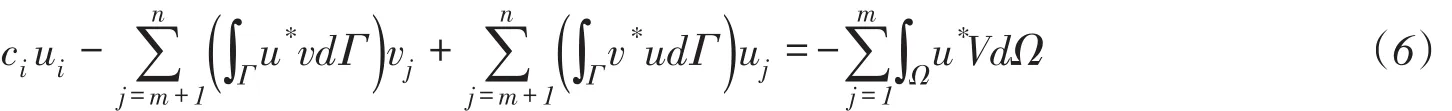
令：

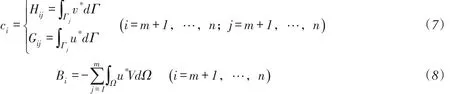
用矩阵符号，可将式（6）表示成［9］：

由定解条件可知，上式（9）含有n-m个未知数，将n-m个未知数组成矢量X，得到新的代数方程组：

将式（10）解得结果代入式（3），反求x，y即得实际运动Z平面的渗流参数。

3 算例与对比分析

某土石坝坝前水深5m，视为无限深透水地基，坝基渗透系数为6.43m/d，允许渗透坡降0.15，悬挂式防渗墙深度为30m，防渗墙距上下游坝角距离分别为10m和35m。求算：（1）坝基平均渗透坡降；（2）上游的单宽入渗流量。

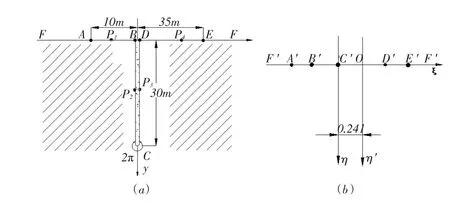
图2 保角变换平面变换图

由保角变换将悬挂式防渗墙转化为如图2，是一个非常容易通过边界元法计算的渗流场边值问题。将场域边界剖分为76个常数单元，其借助边界元软件THBEM2计算坝基内部的水头等值线分布图如图3所示。

并与用有限元法和保角变换解析法计算所得到的水头等值线分布图进行了比较。分别取如图所示的①②③处3个结点的计算值与理论值进行比较如表1。

图3 水头等值线分布图

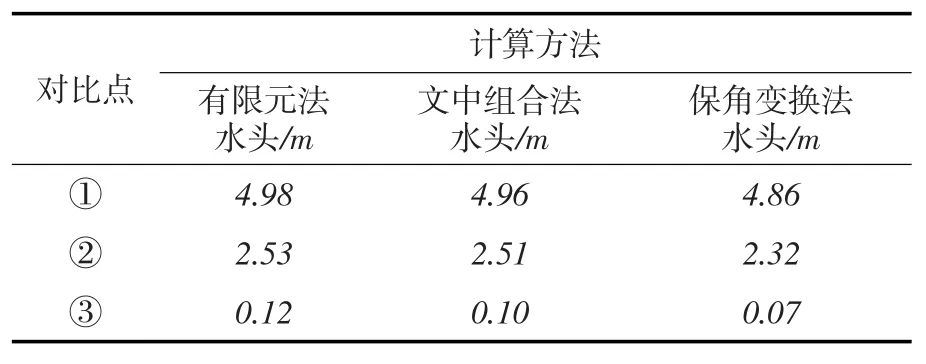
表1 不同计算方法结果比较

计算发现，组合法计算结果能满足计算要求，且相对有限元法计算剖分单元更少，计算更快捷。相比较解析法精度更高。

4 结论

保角变换法与具有诸多优点的边界元法相结合，发挥两种方法的优势，避开了各自的弊端，用于求解复杂渗流场工程问题。通过建立无限深透水地基采用悬挂式防渗墙渗流边值问题进行计算，结果表明：保角变换边界元组合法是一种能有效解决复杂坝基轮廓渗流场数值分析方法，不仅能将复杂的坝基轮廓变得简单，单元剖分少，计算快捷，而且相对与其他方法精度也较高。特别是在处理无限域复杂渗流边界方面优势明显。

［1］ 李志勇.基于保角变换的六角形中子扩散半解析节块法及数值结果［J］.核科学与工程，2014，34（1）：16-22.

［2］ 贾红刚，聂玉峰.各向异性板半无限裂纹平面问题的保角变换解法［J］.应用数学学报，2013，36（2）：243-248.

［3］ 邓琴，郭明伟，李春光，等.基于边界元法的边坡矢量和稳定分析［J］.岩土力学，2010，31（6）：1971-1976.

［4］ 姚振汉，蒲军平，尹欣，等.边界元法应用的若干近期研究［J］.力学季刊，2001，22（1）：10-17.

［5］ 程长征，周焕林，胡宗军，等.近坝基面渗流场的边界元法分析［J］.中国科学技术大学学报，2006，36（12）：1308-1313.

［6］ 周宏伟，张亚衡，李爱民，等.孔隙介质中流体渗流边界演化过程的实验研究［J］.科学通报，2008，53（03）：351-358.

［7］ 田玲玲.直接边界元法及其在地下水渗流问题中的应用［J］.西华大学学报：自然科学版，2006，25（1）：44-45，49.

［8］ 李新强，陈祖煜.三维裂隙网络渗流计算的边界元法及程序［J］.中国水利水电科学研究院学报，2006，4（2）：81-87.

［9］ 柏承新，赵代深.考虑稳定渗流场渗流体积力的弹性问题边界元解法［J］.水利学报，1989（4）：64-69.

Seepage calculation for suspended vertical impervious body on the infinite deep pervious damfoundation based on conformal transformation and boundary element method

MAO Haitao1，3，WANG Zhengcheng1，WANG Xiaoju2，SHAO Dongguo3
（1.Civilengineering instituteofchongqing threeGorgesCollege，Chongqing 404100，China；2.Collegeof environment，HohaiUniversity，Jiangsu 210098，China；3.Wuhan University Instituteofwaterconservancy and hydroelectricpower，Wuhan 430072，China）

The outline of the infinite deep dam foundation is quite complex，and its permeable layer is deep.This unique characteristic determines that it would not be an easy task to guarantee or achieve the calculation accuracy of seepage.Therefore，in terms of the calculating method，conformal transformation& boundary element method is proposed and adopted in this paper to deal with problems which are associated with seepage calculation problem of infinite domain.Conformal transformation method can change complicated dam foundation outline boundary problems to horizontal boundary problem，which will greatly simplify the boundary problem of seepage calculation.Boundary element method shows its great superiority in coping with seepage problem of infinite domain whose boundary is easy to calculate.The combination of the two methods can give full play to their respective advantages.By means of adopting the combination calculation method，the calculated results illustrate the fact that the combination method is much faster and simpler，the result is more accurate and in accordance with the real situation of the infinite field，which provides an approach to dealing with the infinite field seepage problems.

conformal transformation；BEM；infinite field；seepage；dam foundation

TU443

A

10.13244/j.cnki.jiwhr.2017.03.010

1672-3031（2017）03-0223-04

（责任编辑：韩 昆）

2016-04-20

国家自然科学基金项目（51309262）；重庆市科委基础与前沿研究计划项目（cstc2015jcyjA00030、cstc2015jcyjA00022）；重庆三峡学院校企合作项目（15XQ01）；重庆市教委科学技术研究项目（KJ1601024）

毛海涛（1980-），男，山西平陆人，副教授，主要从事土石坝渗流机理研究。E-mail：maohaitao1234@163.com