预应力对风扇转子叶片振动特性的影响

陈官峰，吴光耀，高仁衡，杜文军，段 锟

(中国航发四川燃气涡轮研究院，成都610500)

预应力对风扇转子叶片振动特性的影响

陈官峰，吴光耀，高仁衡，杜文军，段 锟

(中国航发四川燃气涡轮研究院，成都610500)

为研究离心载荷和气动载荷作用对风扇转子叶片振动特性的影响，在考虑预应力的状态下对大尺寸航空发动机风扇转子叶片的振动特性进行了研究。分别考虑几何小变形和大变形条件对预应力的影响，计算并对比分析了不同转速下风扇转子叶片的频率和振型。与叶片实测频率对比表明，考虑大变形条件计算的叶片频率更接近实测频率(仅相差1.82%)，小变形条件计算的叶片频率与实测值最大相差6.88%，扭转振型所对应的频率值差别尤其明显。说明小变形条件分析大尺寸风扇叶片所产生的误差不可忽略，大变形条件下的模态分析更精确。

航空发动机；风扇转子叶片；预应力；大变形；小变形；振动特性；模态分析法

1 引言

高性能航空发动机风扇转子叶片叶型具有薄、大、扭的特点，在高速旋转产生的离心力和气流冲击引起的气动力的作用下易使叶片发生振动，继而产生高周疲劳破坏问题。据统计，航空发动机由振动引起的故障占总故障的60%以上，其中叶片振动故障占总振动故障的70%以上[1]。因此，对风扇叶片振动特性进行精确分析，对航空发动机安全性设计具有重要意义。

目前，国内外对航空发动机风扇叶片的振动特性做了大量研究。寇海军等[2]利用有限元法分析了航空发动机风扇叶片的振动特性，认为在不同转速下叶片的振动特性有较大的不同；Xu等[3]通过有限元分析和试验测量的方法，对轴流式风机叶片由离心和气动载荷引起的振动应力进行了分析和测量；杨雯等[4]对宽弦空心风扇叶片的动力特性进行了研究，从理论上得到了叶片的基本变形以及动态响应情况；张伟等[5]对航空发动机压气机叶片非线性振动进行了研究，其将叶片简化为悬臂薄壁梁，考虑几何大变形影响，利用Hamilton原理建立了叶片的非线性偏微分方程，模拟了气流流速下旋转叶片的动态响应；Yang等[6]推导了一系列包括轴向、横向和扭转运动的耦合积分微分方程来描述旋转的欧拉梁，其中包含离心力引起的刚化作用，即预应力的影响；Carnegie[7]首次用解析的方法研究了旋转叶片的自振频率，并用Rayleigh法得到了理论的势能表达式；楼梦麟等[8]分析了预应力在梁振动过程中的变化，建立了预应力梁横向弯曲振动的微分方程，并通过实例讨论了预应力对梁横向振动的影响；张耀庭等[9]进行了5根全预应力梁的动力试验，结果表明全预应力梁的固有频率随着预应力的增加而增加。然而，这些研究未涉及针对大型风扇转子叶片考虑几何大变形条件下的预应力对叶片振动特性的影响。

本文以某航空发动机风扇转子叶片为研究对象，利用几何大变形和小变形条件下对预应力影响的有限元法，分别计算了叶片的频率及振型，进行了两种条件下计算结果的对比分析，并与试验条件下的实测频率进行了对比。研究成果可为航空发动机风扇转子叶片振动特性的准确分析提供依据。

2 基本理论

阻尼对叶片的模态影响较小，在忽略叶片阻尼情况下，不考虑几何变形条件对预应力影响，有限元法计算转子叶片固有振动特性的振动方程为：

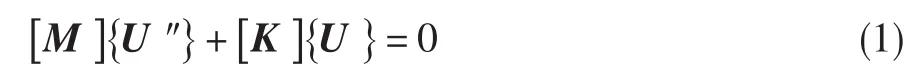
考虑几何大变形和小变形条件对预应力影响，有限元法计算转子叶片固有振动特性的振动方程为：

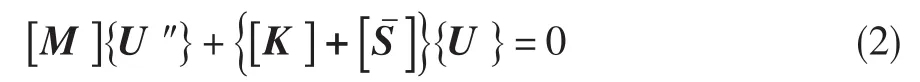
假定叶片振动时为线性多自由度系统，则：

其特征方程为：

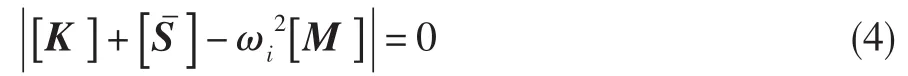
由公式(4)可解得叶片的特征值和特征向量，即叶片的频率和振型。由于公式(4)中含有应力刚度矩阵项，说明应力刚度矩阵的准确性将对叶片的振动特性分析产生影响。工程实践中，往往将应力刚度矩阵分析过程进行近似线性处理，不考虑几何大变形对预应力的影响，这样处理对计算结果的准确性存在一定影响。

3 叶片模型

研究叶片为实心结构，叶身最大高度230.0mm，最大弦宽146.0mm，叶尖最大厚度2.6mm(图1)。叶片材料为钛合金TC11，其部分材料性能[10]见表1。

图1 叶片实体模型Fig.1 Solidmodelofblade

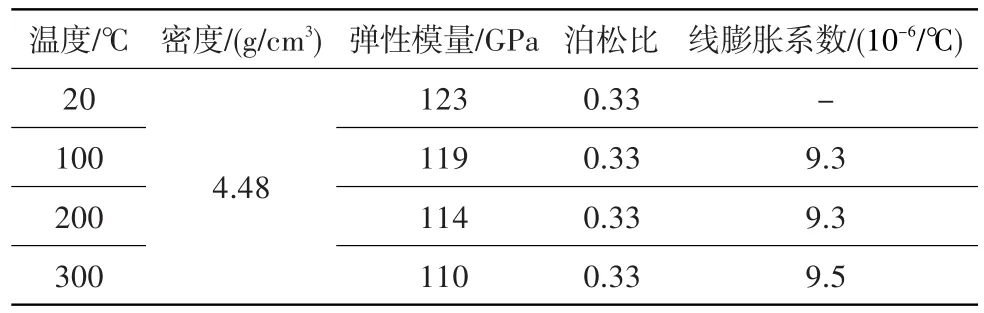
表1 材料性能Table 1 Material performance

由于叶片叶型扭转较大，选用四面体带中节点的单元进行有限元分析，有限元模型见图2。振动分析时，依据叶片的安装方式在叶片榫头挤压面处固支。叶片预应力分析时，考虑叶片的离心载荷、气体流动产生的气动载荷及温度载荷。

4 叶片模态分析

对叶片0 r/min转速下的固有频率(静频）和3 270、4 370、5 430、8 690、9 230、10 310、10 860 r/min转速下的固有频率(动频)进行分析。

4.1 不考虑几何变形模态分析结果

无外载荷作用时几何变形对预应力无影响，此时叶片在0 r/min转速下的前4阶固有频率(静频)见表2，前4阶振型见图3。

图2 有限元模型Fig.2 Finite elementmodel

表2 叶片静频计算结果Table 2 Analysis resultsofblade static frequency

图3 叶片前4阶静频振型Fig.3 Static frequency vibrationmode of first four ordersof the blade

4.2 考虑几何变形模态分析结果

分别考虑几何大变形和几何小变形对预应力的影响，对叶片进行模态求解。

4.2.1 几何小变形

对模型施加离心载荷、气动载荷和温度载荷，在转速3 270、4 370、5 430、8 690、9 230、10 310、10 860 r/min处分别进行模态分析，考虑几何小变形对预应力的影响，得到的叶片前4阶频率见表3，转速10 860 r/min时叶片前4阶的振型见图4。

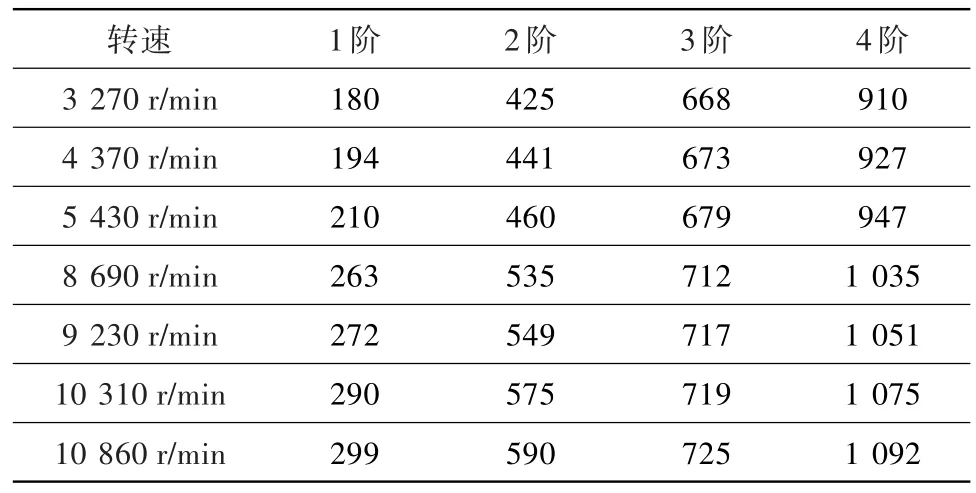
表3 几何小变形预应力条件下的叶片动频结果 Hz Table 3 Analysis resultsofblade dynamic frequency based on small deformation prestressing

图4 10 860 r/min转速下叶片前4阶动频振型(几何小变形)Fig.4 Dynamic frequency vibrationmode of first four ordersof the blade at10 860 r/min(small deformation)

4.2.2 几何大变形

对模型施加离心载荷、气动载荷和温度载荷，在转速3 270、4 370、5 430、8 690、9 230、10 310、10 860 r/min处分别进行模态分析，考虑几何大变形对预应力的影响，得到的叶片前4阶频率见表4，转速为10 860 r/min时叶片前4阶的振型见图5。

图5 10 860 r/min转速下叶片前4阶动频振型(几何大变形)Fig.5 Dynamic frequency vibrationmode of first four ordersof the blade at10 860 r/min(large deformation)

表4 几何大变形条件下的叶片动频结果 HzTable 4 Analysis resultsofblade dynamic frequency based on large deformation prestressing

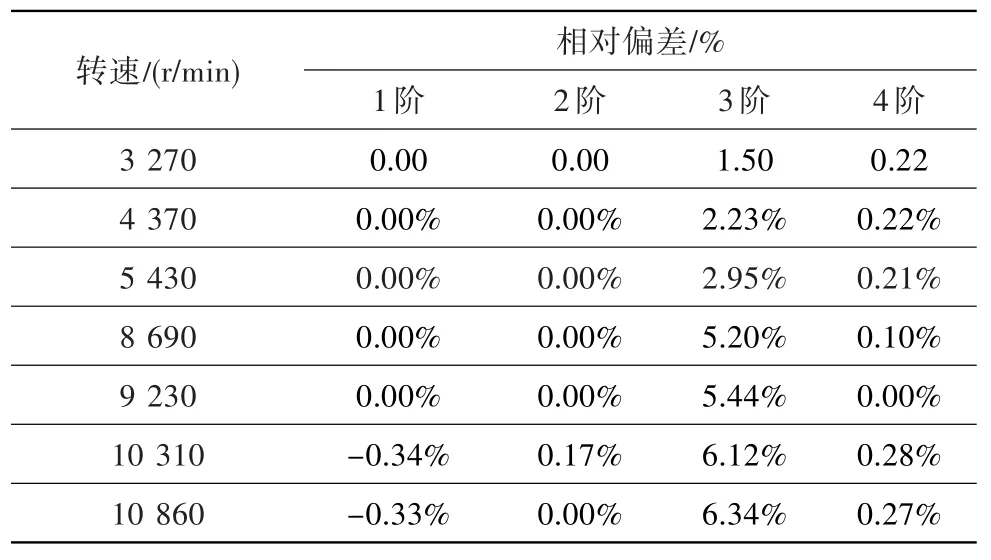
表5 频率相对偏差分析结果Table 5 Deviation analysis result

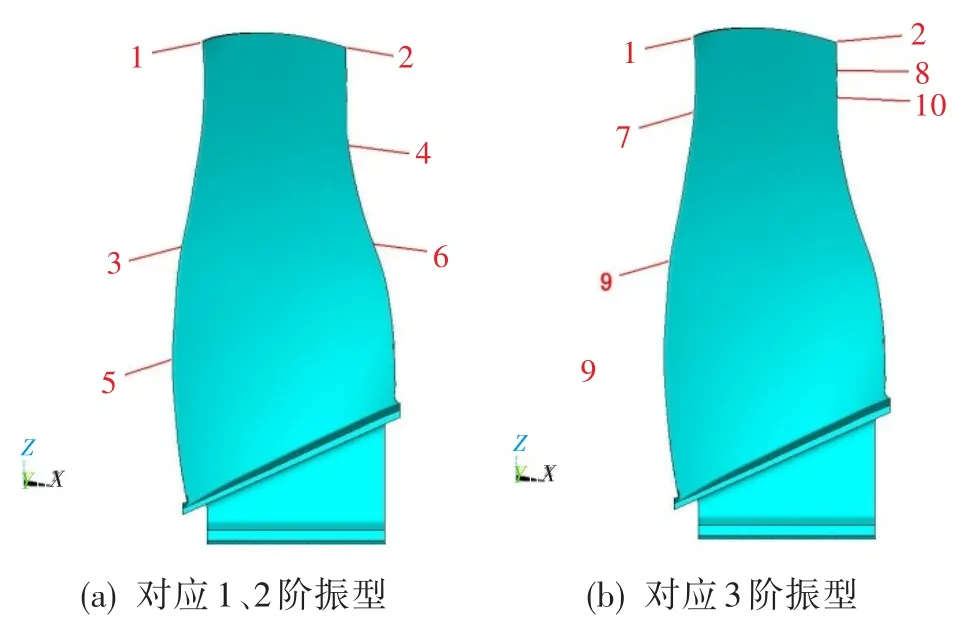
图6 特征点位置示意图Fig.6 Sketchmap of feature points

4.3 结果分析

4.3.1 频率结果分析

为更直观反映几何大变形和小变形条件对频率结果的影响，对其进行了相对偏差分析。采用的公式为：

式中：δ为相对偏差，F大、F小分别为几何大变形和几何小变形条件下叶片的动频。

偏差分析结果见表5。可见，小变形和大变形条件对叶片的1、2阶频率分析结果没太大影响，最大偏差为0.34%；对3阶频率影响较大，最大偏差为6.34%。从振型上看，叶片1、2阶为弯曲振型，3阶为扭转振型，4阶为复合振型。据此可得，大变形条件对叶片的弯曲振型频率几乎没影响，对复合振型的频率影响较小，对扭转振型的频率影响较大。

4.3.2 振型结果分析

为研究叶片在几何小变形和大变形对预应力影响作用下的叶片振型变化，分析了叶片前3阶振动的相对振动位移。根据叶片振型选取了提取位移的特征点，其位置见图6。

各特征点的相对位移对比见表6。可见，对于1阶振型，选取的各特征点的位移几乎没有变化，说明其振型没有变化；对于2阶振型，相对于小变形条件下分析的振型，大变形条件下其叶尖前缘位移增大，叶尖尾缘位移减小，其余位置变化不明显；对于3阶振型，叶片前缘的位移分布变化较大，叶片尾缘的位移分布变化较小。

综上所述，考虑几何大变形分析叶片预应力后，对风扇叶片的模态产生了影响，其中对扭转振型对应的阶次频率影响较大，不可忽略；对叶片的二弯振型也有一定的影响。

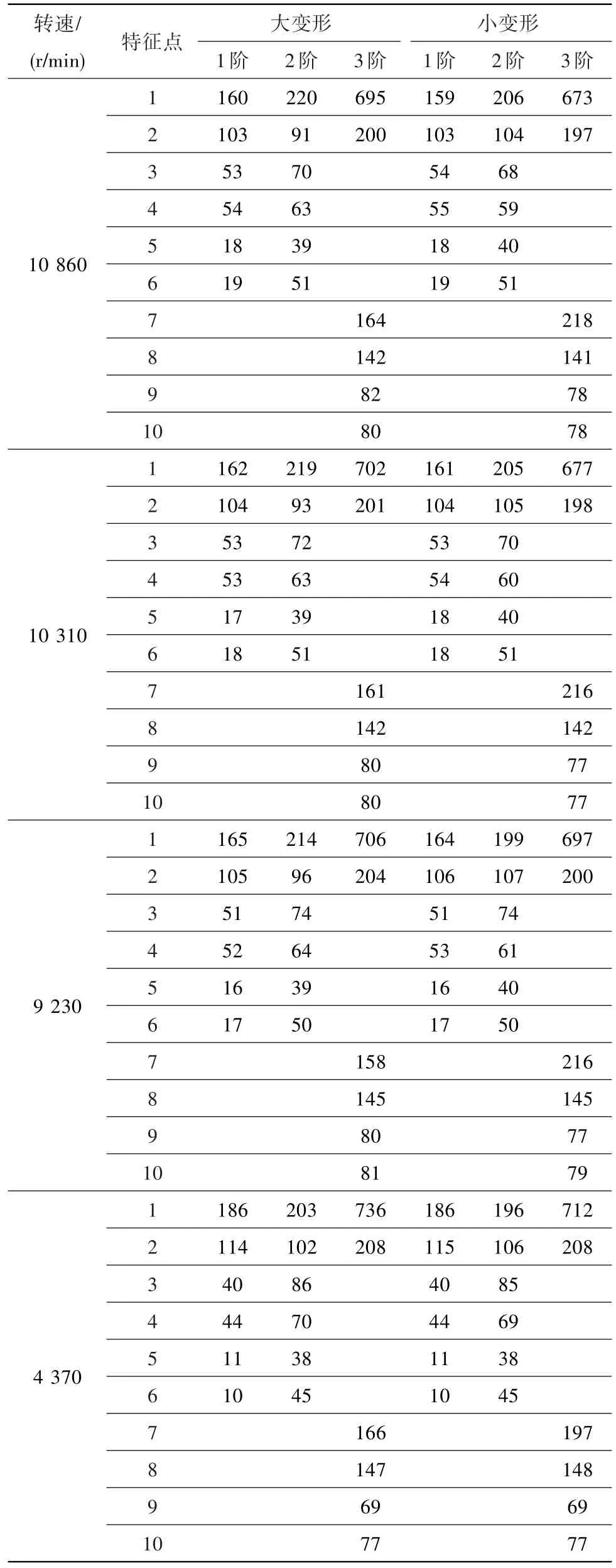
表6 几何大变形和小变形条件下前3阶特征点位移对比Table 6 The contrastof feature points displacementof first threeordersbetween large and small deformation prestressing

5 试验结果

5.1 试验测量结果

为研究几何大变形和小变形对叶片动频的影响，在风扇试验件中利用应变片对叶片的振动进行监测。应变片分布见图7，位置如图中A、B、C、D所示。试验测得叶片在不同转速下应变监测点A、D的应变频谱图见图8。

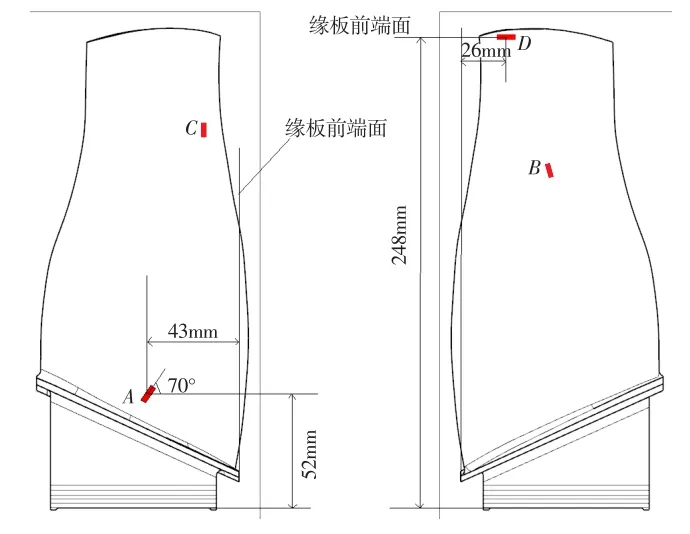
图7 应变片粘贴示意图Fig.7 Sketchmap of strain gage

分析所测应变频谱图，得到叶片不同转速下动频的实测值(平均值)，见表7。可见，叶片的实测各阶频率值均随着转速的提高而提高，变化趋势与有限元分析动频结果相同。

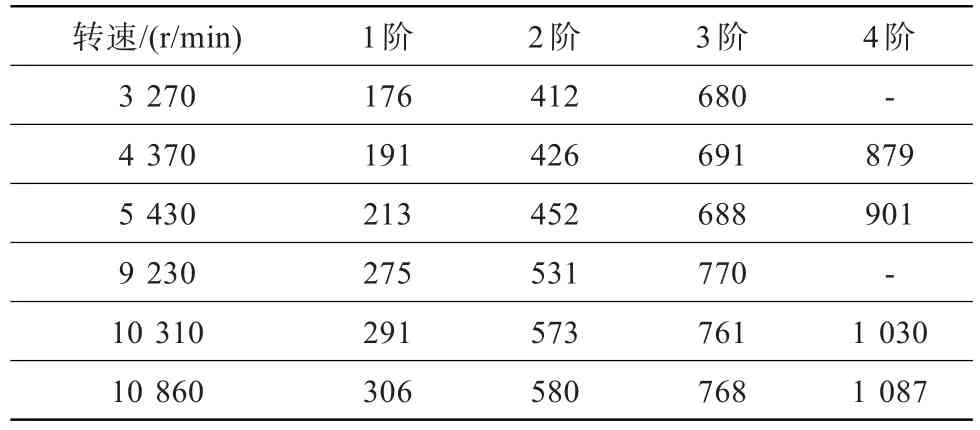
表7 叶片动频实测值 HzTable 7 Measured value ofblade dynamic frequency

5.2 实测结果与有限元分析结果的对比

以实测结果为标准值，分别对几何大变形和小变形条件下的频率分析结果进行误差分析，结果见表8。可见，对于3阶振动频率，考虑大变形条件的频率误差最大为1.82%，而小变形条件的最大误差为6.88%，其他阶次误差均相当。因此，对于风扇叶片，大变形条件下的模态分析相对于小变形条件更加精确，且小变形分析叶片振型产生的误差不可忽略。

6 结论

(1) 叶片动频分析中，几何大变形和小变形对叶片的弯曲振动频率几乎没有影响，对扭转振动频率影响较大。

(2)叶片振型分析中，几何大变形和小变形对叶片的二弯振型也有一定的影响。

(3)对于风扇叶片，几何大变形相对于几何小变形模态分析更加准确，且几何小变形条件分析叶片振型产生的误差不可忽略。

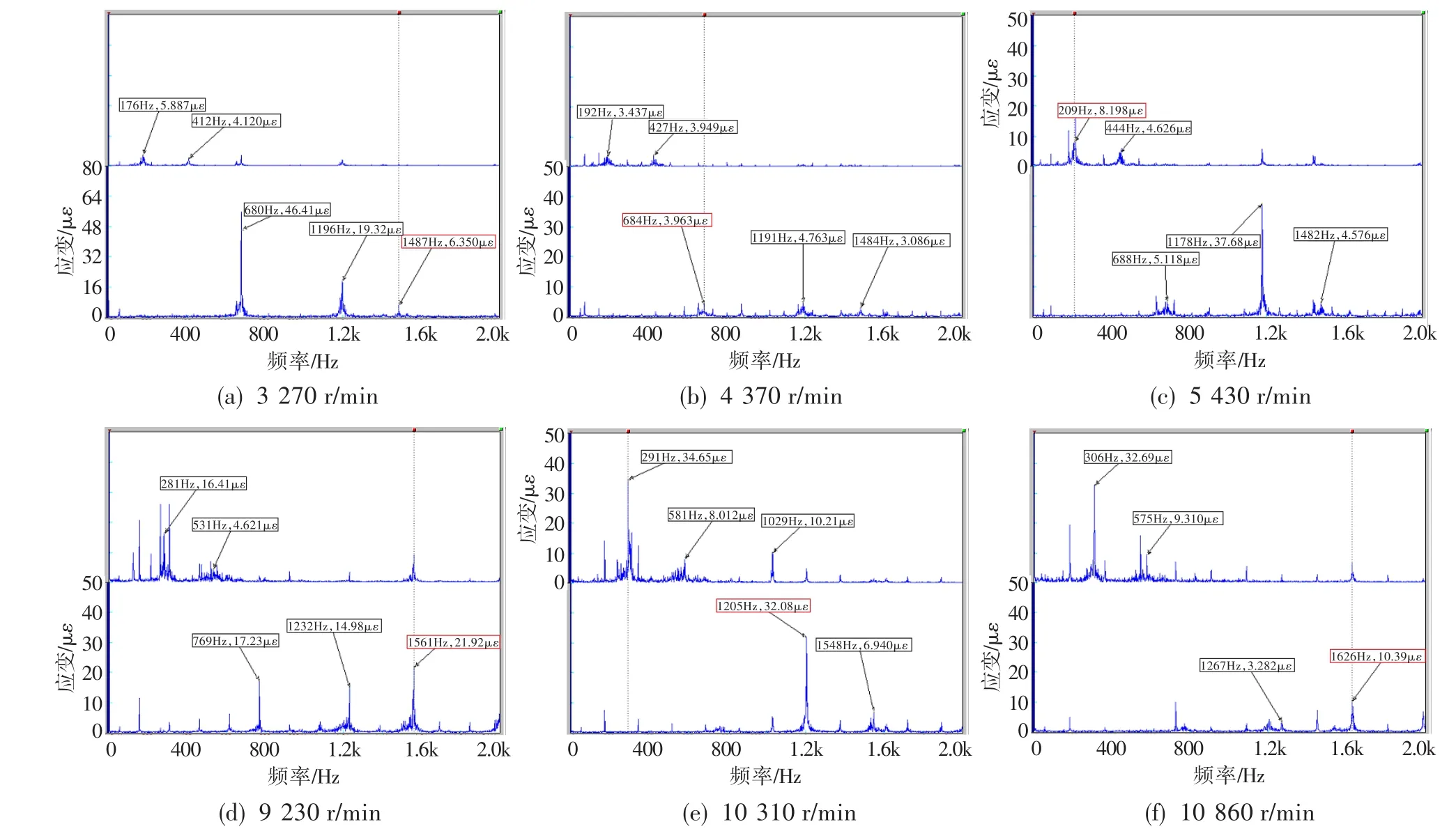
图8 不同转速下A、D测点的频谱图Fig.8 Strain spectrum ofmeasurementstation A,D atdifferent rotating speeds

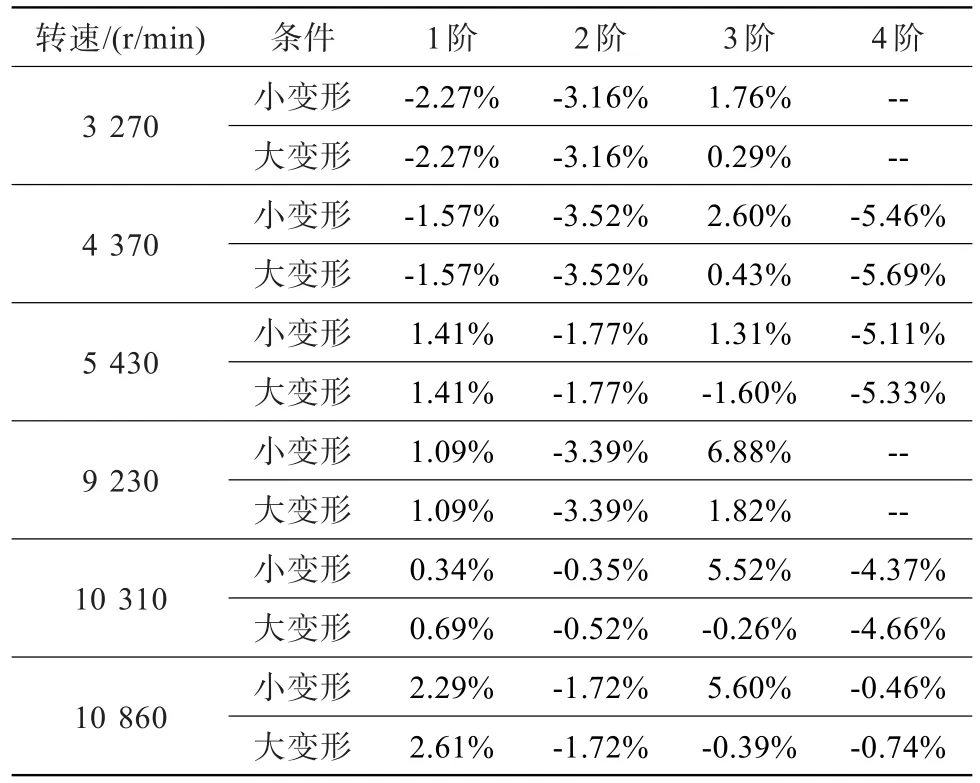
表8 有限元分析值与实测值误差分析结果Table 8 Error analysisof theoretical value andmeasured value

[1]蔡肇云，金六周.航空发动机强度设计､试验手册：叶片强度与振动计算[K].北京：第三机械工业部第六研究院，1980：34—50.

[2]寇海军，张俊红，林杰威.航空发动机风扇叶片振动特性分析[J].西安交通大学学报，2014，48(11)：109—114.

[3]Xu C，Amano R S，LEE E K.Investigation of an axial fan-blade stress and vibration due to aerodynamic pres⁃sure field and centrifugal effects[J].Fluids and Thermal Engineering，2004，47(1)：75—90.

[4]杨 雯，杜发荣.宽弦空心风扇叶片动力响应特性研究[J].航空动力学报，2007，22(3)：444—449.

[5]张 伟，冯志青，郭翔鹰.航空发动机压气机叶片的非线性振动问题[J].中国科学，2013，43(4)：345—362.

[6]Yang J B，Jiang L J，Chen D C.Dynamic modelling and control of a rotating Euler-Bernoulli beam[J].Journal of Sound and Vibration，2004，274(3-5)：863—875.

[7]CarnegieW.Vibrationsof rotating cantilever blading:theo⁃retical approaches to the frequency problem based on ener⁃gymethods[J].JEng Sci，1959，1(3)：235—240.

[8]楼梦麟，洪婷婷.预应力梁横向振动分析的模态摄动方法[J].工程力学，2006，23(1)：107—111.

[9]张耀庭，汪霞利，李瑞鸽.全预应力梁振动频率的理论分析与试验研究[J].工程力学，2007，24(8)：116—120.

[10]中国航空材料手册编委会.中国航空材料手册第四卷：钛合金铜合金[K].2版.北京：中国标准出版社，2002.

In fluence of p restressing on the vibration characteristicsof fan b lade

CHENGuan-feng，WUGuang-yao，GAORen-heng，DUWen-jun，DUAN Kun
(AECCSichuan Gas Turbine Establishment，Chengdu 610500，China)

To study the influence of centrifugal force and aerodynamic load on the vibration characteristics of fan blade,the vibration characteristicsofa large sized aero-engine fan bladewere studied taking the pre⁃stressing force into account.Considering the impact of small and large geometric deformation on the pre⁃stressing,the frequencies and modes of the fan blades at different speeds were calculated and analyzed. Compared with themeasured frequency of blade,the blade frequencies calculated with the large deforma⁃tion were the closest to themeasured value(only 1.82%discrepancy value).The blade frequencies calculat⁃ed with small deformation had themaximum difference value of about 6.88%compared with themeasured value.The corresponding frequency difference of torsion mode was particularly obvious,implying that the error caused by small deformation prestressing in the analysis of large sized fan blades cannot be ignored. Themode analysis ismore accurate under the condition of large deformation.

aero-engine；fan rotorblade；prestressing；large deformation；small deformation；vibration characteristic；mode analysis

V231.92

A

1672-2620(2017)03-0029-06

2016-05-11；

2016-09-06

陈官峰(1983-)，男，河南登封人，工程师，硕士，主要从事航空发动机叶片强度振动研究。