奇偶模分析法分析定向耦合器
戢予 赖秋宇 拉富珍 陈渝龙 重庆邮电大学光电工程学院重庆国际半导体学院
奇偶模分析法分析定向耦合器
戢予 赖秋宇 拉富珍 陈渝龙 重庆邮电大学光电工程学院重庆国际半导体学院
基于定向耦合器的相关理论基础,采用奇偶模分析法,引用传输线定理,对定向耦合器的数学模型进行具体分析。通过理想3dB定向耦合器的设计,改变定向耦合器的物理尺寸,选择确定合适的特性阻抗,验证了设计方案的正确性。
奇偶模 定向耦合器 传输线定理
1 理论基础
1.1 奇偶模分析法
在对面对称网络进行分析时,可以先把它看作是等值同相激励的偶模结构(即在对称面开路)进行计算,再把它看成是等值反相激励的奇模结构(即在对称面短路)进行计算,最后运用叠加定理,把偶模结构和奇模结构下得到的结果线性相加,则可以得到网络的总的固有特性参量。
也就是说,我们可以视为同时有以下两组信号分别激励同一个二端口网络(ae是偶模激励,ao是奇模激励):
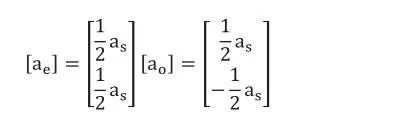
又因为b=Γa(b为归一化反射波,Γ为反射系数),于是可以得到:

当不使用波参量而使用电路参量时,把激励a替换为电流I,把响应b替换为电压V,同理可得:
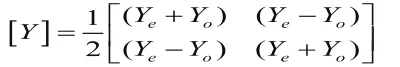
1.2 S矩阵与归一化A矩阵的转换关系
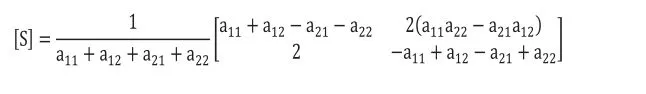
1.3 定向耦合器
假设有这样一个定向耦合器,它的四个端口归一化特性导纳为Y01=Y02=1,分支线归一化特性导纳为Y0B=a,分支线间的主线的归一化特性导纳为Y0A=b,分支线及其之间的主线长度为l=λ/4,电路模型如下图所示:
(1)信号仅从①口输入,到达端口③的信号为两路的叠加,一路是A->D,波程为λ/4,另外,一路由A->B->C->D,波程为3λ/4,两路信号波程差为λ/2,也就是说相位差为π,所以两路信号相互抵消。如果两路信号幅度相等,则端口③无输出,即与端口①隔离,所以端口③称为隔离端。
(2)信号仅从①口输入,到达端口④的信号为两路的叠加,一路是A->D->C,行程为λ/2,另外,一路由A->B->C,行程也是λ/2。因为端口④能根据两路信号叠加的强弱来输出能量,所以端口④称为耦合端。


图1 定向耦合器
2 分析
假设直接利用图1所示定向耦合器(归一化导纳a,b是未知量)进行分析,则我们可以根据它的面对称性应用奇偶模分析法进行分析。在偶模激励状态下,把模型按对称面上下隔开,并在对称面处开路,如图2所示:

图2 偶模情况下的模型
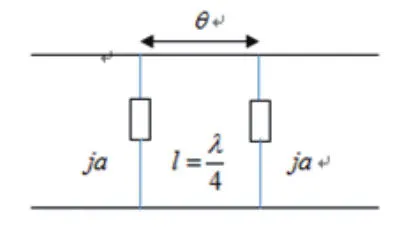
图3 偶模情况下的等效电路
因为分支线间的主线部分特征导纳为a,根据传输线定理,我们可以把它视为开路经过λ/8折合到A处的导纳,即为ja。又因为偶模情况下的B处的分支线与A类似,同理可得B处导纳也为ja,于是可以得到图3所示等效双端口电路。把这个电路视为由三个已知的典型电路级联而成,它们分别是并联导纳、传输线段、并联导纳。它们三个电路的A矩阵查表可知,又因为整个电路的总A矩阵则为三个电路的A矩阵之积,于是可以得到:
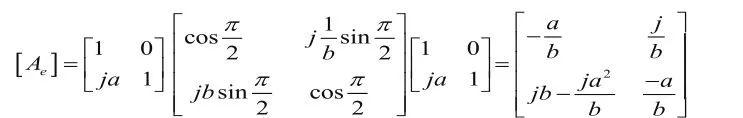
利用上述理论准备中的S矩阵与A矩阵的转换关系可以得到S矩阵,所以电路在偶模激励下的S矩阵为:
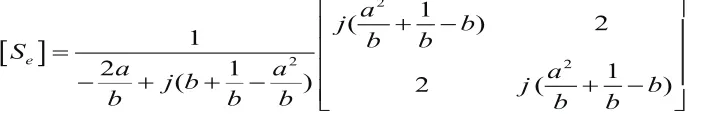
在奇模激励状态下,模型从对称面上下隔开,并把隔开的对称面短路。根据传输线定理,我们可以把它视为短路线经过λ/8折算到A处的导纳,即为-ja。又因为B处的分支线与A处的分支线长度相同,所以B处的导纳也为-ja。同样利用之前得到的等效电路模型,把导纳值ja替换为-ja即可计算出奇模情况下的S矩阵:
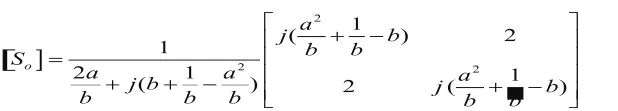
假设该定向耦合器是理想的3dB定向耦合器,那么它的回波损耗则为0(即S11=0)、隔离端口无输出(即S31=0)、且耦合度为3dB。又因为耦合度为3dB,根据定向耦合器的相关公式可以得到:。于是综合上述所有条件并应用奇偶模分析法推导出的结论,可以得到以下方程组:
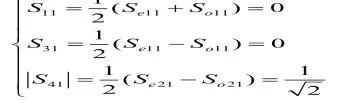
3 总结
定向耦合器是一种常用的微波器件。本文介绍了用奇偶模分析法这种网络分析方法对耦合器进行了分析,并对3dB定向耦合器进行了具体计算。根据设计要求的不同,需要选择尺寸及特性阻抗,当然,这种分析方法亦可以应用到所有面对称网络中去。
[1]徐锐敏.微波网络及其应用.科学出版社[M],2010,(07)
[2]田步宁.微波网络分析技术新进展及其应用研究[D].西安电子科技大学,2002

