基于蒙特卡洛的航空发动机试飞数据模型误差容限分析

姜健

(中国飞行试验研究院发动机所，西安710089)

基于蒙特卡洛的航空发动机试飞数据模型误差容限分析

姜健

(中国飞行试验研究院发动机所，西安710089)

将发动机实时趋势监控中的误差容限划分成两部分，一部分由发动机工作包线内的模型建模误差导致，一部分由发动机工作参数的不确定性导致。建模误差的影响采用包线内最大预测误差，由参数不确定性引起的误差采用蒙特卡洛分析确定。将不同概率分布下的测量参数作为发动机模型的输入参数，采用蒙特卡洛策略分析模型预测值的均值和标准差分布，采用3σ置信水平作为因测量不确定性引起的误差容限。选取未参与发动机模型辨识的整个飞行架次的试验数据进行验证，结果表明考虑输入参数不确定性后，模型误差带的分布更为合理。该技术可用于航空发动机飞行试验中，提前发现发动机工作中的异常现象，可提高发动机飞行试验的质量和效率。

飞行试验；航空发动机；模型辨识；蒙特卡洛分析；趋势监控；误差容限分析

1 引言

航空发动机尤其是军用航空发动机多工作在机械、热力、气动等的极限状态，参加飞行试验科研或定型的航空发动机的技术状态仍处在不断调整和成熟的过程中，在实际飞行试验过程中更容易出现故障和问题。为提高飞行试验过程的安全性，有必要对航空发动机进行实时状态监控[1-3]。在航空发动机飞行试验过程中，通过专用的测试系统沿流程测量发动机大量工作参数，基于发动机参数的模型预测值与实测值确立监控残差，实现试飞过程的趋势监控，可以在发动机工作参数出现异常时，即故障出现征兆时发出警告，并采取合适的措施将故障消除在发展状态，通过这种方式可有效提高试飞安全性，提升试飞的质量和效率[1，4-9]。

误差容限直接影响航空发动机趋势监控模型的表现性能，因此需要基于发动机实时趋势监控确立相应的故障判故告警门限。只有选择合适的告警门限才可以既能提前发现故障表现的征兆，又不会报出很多的虚假故障[10-14]。本文基于人工神经网络建立了某型涡扇发动机实时趋势监控模型[1，3，5-9，15-18]，基于蒙特卡洛分析确立了实时趋势监控模型的自适应告警门限[19]，对促进涡扇发动机实时趋势监控技术的应用有着重要的意义。

2 航空发动机全状态趋势监控模型

文中采用NARX非线性系统分析技术，并利用人工神经网络代替航空发动机NARX模型中的非线性函数Fnl，确立发动机全状态趋势监控模型。该模型综合考虑了试飞数据中包含的历史数据信息，其结构[1，8，13，15-16]为：

式中：Fnet为合适的人工神经网络函数，如图1所示。

该型发动机模型辨识研究的参数包括：高压转子转速nH，低压转子转速nL，低压涡轮出口总温T6，低压涡轮出口总压 p6，低压压气机导向叶片角度α1，高压压气机导向叶片角度α2，高压压气机出口压力p31，主燃油总管压力 pf，尾喷口喉部直径D8，滑油总回油温度Tole。通过特性分析法建立模型的输入输出参数信息，如表1所示。其中输入参数包括气压高度Hp、飞行马赫数M a、大气总温TTB、油门杆角度ϕ和作战训练信号Gstr。

表1 航空发动机非线性模型输入输出参数信息Table 1 The inputand output information ofaero-engine NARXmodel

发动机全状态模型采用三层前向神经网络结构，其中高压转速、低压转速、涡轮后温度神经网络模型的输入输出延迟特征及隐含层神经元数目见表2。

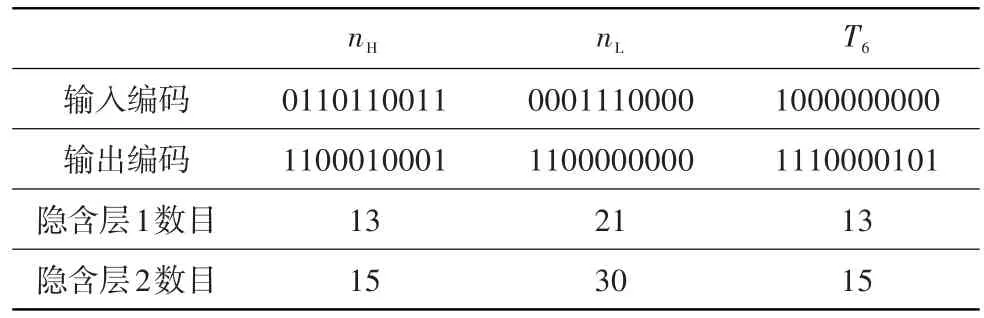
表2 发动机神经网络模型结构参数设置Table 2 The structure parameter settingsofaero-engine neuralnetworkmodel

利用辨识模型在全部试飞数据样本上的预测值与实测值之间的差值作为模型建模误差。若辨识模型具有可靠精度，则其预测误差的分布应服从正态分布特性。发动机高压转速、压气机后压力、涡轮后温度以及滑油总回油温度模型的误差统计特性如表3所示。

3 参数测量统计特征估计

假定θ为概率函数 f的参数向量，可以将概率密度函数记作 fθ。若从潜在分布中抽取的数据样

表3 航空发动机辨识模型建模误差的统计特性规律Table 3 The statistic characteristicsofmodeling error ofaero-engine identifiedmodel

本分别为x1，x2，…，xn，则样本的似然函数为：

在给定分布参数情况下，其可看作是数据的联合概率密度函数。假定每个数据样本点的独立特征，可以将其写作：

最大似然估计方法可看作是一种非线性无约束优化问题，即：

发动机飞行试验过程中测量的工作参数分布fY满足：fY～N(0 ,σY)。基于最大似然估计得到发动机参数测量的标准差σY，见表4。

表4 发动机工作参数测量的标准误差Table 4 The standard deviation ofaero-engineworking parameters

4 基于蒙特卡洛分析的发动机模型预测容限确定

动态过程中的基于蒙特卡洛方法的试飞数据模型误差评定步骤如下：

(1)建立航空发动机的试飞数据模型——本文采用的是基于神经网络的某型涡扇发动机全状态实时趋势监控模型y=Fnet(u1,u2,…,un)；

(2)建立该涡扇发动机实时趋势监控模型各输入参数的不确定度分布的概率密度gi(u)(i =1,2,…n)；

(3)确定抽样样本容量N，并对各输入参数的概率密度分布进行抽样，产生满足指定概率密度函数 gi(u)(i =1,2,…n)的随机数；

(4) 计算各分量的样本值y1，y2，…，yN，并求出对应的样本均值，计算此时的标准不确定度

(5)计算趋势监控模型的实时不确定度时，针对每一时刻t重复步骤(2)～(4)，即可得到实时趋势监控过程中的参数误差容限。

5 非样本点性能验证

选择初始飞行条件(Hp0，Ma0，TTB)，对高压转子转速进行蒙特卡洛仿真以确定仿真迭代次数，结果如图2和图3所示。可见，进行1 000次迭代即可达到所需要的求解精度。

选取未参加涡扇发动机实时趋势监控模型构建的一次完整飞行试验数据，利用之前辨识得到的发动机全状态仿真模型，采用前面讨论的模型输入参数概率分布模型，在每一个数据点上运行蒙特卡洛模拟，最终得到仿真模型在整个飞行数据上的均值和方差分布。依此为基础叠加上模型建模误差，即可得到发动机的整个试飞架次上的误差分布。飞行过程中的飞行高度、飞行马赫数、大气总温、油门杆角度的变化范围如图4所示。

该涡扇发动机高压转速、压气机出口压力、涡轮出口总温、滑油总回油温度模型检验结果及误差分布如图5～图8所示。图中红线为上边界线，蓝线为下边界线，黑色圆点为实际飞行试验数据，绿线为模型预测数据。从图中可以看出，采用柔性误差带可很好地考虑模型建模误差和参数测量误差，从而降低模型预测结果的不确定性。实际的实时趋势监控过程中，相比当前使用的硬门限告警方式，当发动机实际工作参数超出给定上、下限之后，即可认为发动机工作出现异常，此时试飞工程师可提醒飞行员采取合适措施降低或消除严重故障的发生。

6 结论

基于某型涡扇发动机全状态实时趋势监控模型，利用蒙特卡洛仿真分析技术，对存在输入参数不确定性条件下的模型误差分布进行了讨论，确立了发动机模型柔性误差带，并形成如下结论：

(1)基于蒙特卡洛仿真分析技术可以全面考虑因输入参数不确定性引起的模型预测误差，可提高模型误差带确定的精确性；

(2)蒙特卡洛仿真分析所需计算量较大，后面可考虑迭代或自适应技术实现模型误差带的实时确定。

参考文献：

[1]潘鹏飞，马明明，许艳芝．基于飞行试验数据的双转子航空发动机加减速瞬态模型辨识[J].航空发动机，2016，42(3)：78—81.

[2]Isermann R，Munchhof M.Identification of dynamic sys⁃tems-an introduction with applications[M].Berlin：Spring⁃er，2015.

[3]Lazzaretto A，Toffolo A.Analytical and neural network models for gas turbine design and off-design simulation[J]. International Journal of Applied Thermodynamics，2001，(4)：173—182.

[4]Gennady,Haydn.Dynamicmodeling of gas turbines:iden⁃tification,simulation,condition monitoring and optimal control[M].Berlin：Springer，2004：131—155.

[5]Sjöberg J，Zhang Q.Nonlinear black-boxmodeling in sys⁃tem identification:a unified overview[J].Automatica，1995，31：1691—1724.

[6]Ruano A E，Fleming P J.Nonlinear identification of air⁃craft gas-turbine dynam ics[J].Neurocomputing，2003，55：551—579.

[7]Sina T，Sadough ZN.Dynamic neural network-based fault diagnosis of gas turbine engines[J].Neurocomputing，2014，125：153—165.

[8]Mohamed O M，Mhiri R.An approach to polynomial NARX/NARMAX systems identification in a closed-loop with variable structure control[J].International Journal of Automation and Computing，2008，(5)：313—318.

[9]Joly R B，OgajiSO T.Gas-turbine diagnosticsusing artifi⁃cial neural-networks for a high bypass ratiomilitary turbo⁃ fan engine[J].Applied Energy，2004，78：397—418.

[10]Fast M，Assadi M.Development and multi-utility of an ANN model for an industrial gas turbine[J].Applied Ener⁃gy，2009，86：9—17.

[11]Chiras N，Evans C.Nonlinear modeling and validation of an aircraftgas turbine engine[J].IFACProceedings，2001，34：871—876.

[12]Chiras N，Evans C，Rees D.Nonlinear gas turbinemodeling using feedforward networks[R].ASME GT-2002-30035，2002.

[13]Jurado F.Nonlinear modeling of micro-turbines using NARX structureson the distribution feeder[J].Energy Con⁃version and Management，2005，46：385—401.

[14]Billings S A.Introduction to nonlinear systems analysis and identification[J].Lecture Notes in Control&Informa⁃tionences，1985，79(1)：263—294.

[15]Eric H K，WongY K.Modelling and prediction ofmachin⁃ing errors using ARMAX and NARMAX structures[J].Ap⁃plied MathematicalModelling，2003，17：611—627.

[16]Yang G，Meng J.NARMAX time seriesmodel prediction: feedforward and recurrent fuzzy neuralnetwork approaches [J].Fuzzy Setsand Systems，2005，150：331—350.

[17]Alireza R，Scott S.Identification of nonlinear systems us⁃ing NARMAX model[J].Nonlinear Analysis，2009，71：1198—1202.

[18]Gupta M M，Homma N，Liang J.Static and dynamic neural networks:from fundamentals to advanced theory[M].USA：W iley Interscience，2003：106—163.

[19]Robert CP，Casella G.Monte Carlo statisticalmethods[M]. Berlin：Springer：2004:105—112.

Error bound analysisof aero-engine data-d rivenm odelbased on M onte Carlo sim u lation

JIANG Jian
(Engine Flight Test Technology Institute ofChinese Flight Test Establishment，Xi’an 710089，China)

Themodel error bound is classified into two parts,one is resulted bymodeling error in aero-en⁃gine working envelope,and the other is determined by themeasurementuncertainty ofworking parameters. Themaximum predicted modeling error was used as first part of error bound,and the second error bound was determined by Monte Carlo analysis.Themeasurement parameters,each ofwhich has own probability distribution,have been used as inputof aero-enginemodel,and the 3σconfidence intervalwas taken as er⁃ror bound resulted bymeasurementuncertainty.The result has been validated on extra flight test data,and it is shown thatwith the consideration ofmeasurementuncertainty,the error bound ismore reasonable.This method could be applied in aero-engine flight test to detect abnormal state in advance,which could im⁃prove the quality and effectivenessofaircraft flight test.

flight test；aero-engine；model identification；Monte Carlo analysis；trendmonitoring；error bound analysis

V232.2

A

1672-2620(2017)03-0001-05

2016-10-25；

2017-05-12

姜 健(1980-)，男，陕西汉中人，高级工程师，硕士，主要从事航空发动机飞行试验技术研究工作。