裂缝性油藏注水井压降试井解释方法及应用

姜永，张雷，别旭伟，王迪，黄磊

（中海石油（中国）有限公司天津分公司，天津 300459）

裂缝性油藏注水井压降试井解释方法及应用

姜永，张雷，别旭伟，王迪，黄磊

（中海石油（中国）有限公司天津分公司，天津 300459）

为了更加准确地描述裂缝性油藏注水井的动态特征，得到更多关于地层和测试井的可靠信息，基于Buckley-Leverrett饱和度分布方程，建立了裂缝性油藏注水井压降试井解释模型，并对模型进行了数值求解，获得了裂缝性油藏注水井压降试井典型拟合图版。根据压降导数曲线特征，将流动过程划分为7个流动段：井筒储集效应阶段、表皮效应阶段、基质向裂缝窜流阶段、水区径向流阶段、油水两相区响应阶段、总系统径向流阶段和边界响应阶段。油、水黏度差异会导致双对数曲线上翘。建立的试井解释模型可计算注水前缘的位置，分析注水井周围地层信息及边界情况。研究结果对注水井的动态评价、注水方案的设计具有重要意义。

裂缝性油藏；注水井；试井；数学模型

0 引言

注水开发是提高油田采收率的重要手段之一，了解注水井的动态对合理开发油田具有重要的意义。通过注水井试井可获取油水相渗透率、注水井周围污染情况、注水前缘距离、油藏边界等信息，并且相对于油井测试，注水井测试比较简单，不影响油田的产量。尤其对于原油黏度较高的油田，油井测试需要更长时间，而通过注水井测试了解其开发动态更加便捷。但由于注水地层的渗流情况比单相渗流更加复杂，因而给注水井试井带来了诸多困难和挑战。

关于注水井试井解释方法，国内外许多学者开展了相关研究工作［1-2］。 巨亚锋［3］建立了综合考虑井筒储存效应、表皮效应、启动压力梯度、渗透率非均质性等影响因素的低渗两区复合油藏注水井试井解释数学模型。李乃华［4］建立了多层均质定压边界灌注试井数学模型，针对适用于现场的折线型灌注函数，获得了层间及井底压降的实空间精确解析表达式。尹洪军［5］介绍了各种注水井的物理模型及试井曲线，提出了结合地质、测井等资料，合理利用典型曲线分析注水井试井资料的方法。刘佳洁［6］根据质量守恒原理，结合注水井岩心归一化相渗曲线，建立含水饱和度与相对渗透率关系，以油水两相流渗流理论为基础，建立了地层流体复合注水井试井模型。

虽然关于注水井试井的研究已有许多成果，但有关裂缝性油藏注水井压降试井解释方法研究较少。为了更好地掌握裂缝性地层渗流动态信息，为注水井的增注措施提供依据，基于Buckley-Leverrett饱和度分布方程，建立了裂缝性油藏注水井压降试井解释模型，并对模型进行了数值求解，获得了裂缝性油藏注水井压降试井理论典型拟合图版。对评价注水井的动态、设计注水开发油田注水井方案具有重要的指导意义。

1 裂缝性油藏注水井试井解释模型

1.1 注水阶段的物理模型

油藏注水开始后不久，由于油水性质的差异，在油藏内会形成流体的饱和度梯度。注水井周围，含水饱和度会非常高（水相带），从注水井到注水前缘，饱和度逐渐降低（油水过渡带），注水前缘以外为纯油区。随着注入水的不断推进，油藏内流体饱和度的分布会不断发生变化。对图1模型作以下假设：1）地层水平等厚，油藏由裂缝系统和基质系统组成；2）以恒定速率注水；3）流体和岩石微可压缩，且压缩系数为常数；4）流体在地层内的流动为等温流动，渗流满足达西定律；5）忽略重力和毛细管力影响；6）考虑井储和表皮系数影响；7）水驱油为非活塞式的，饱和度分布满足Buckley-Leverrett方程。

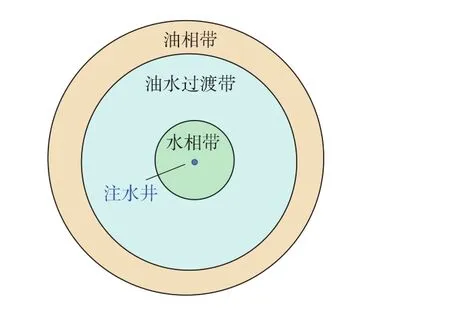
图1 注水井模型示意

1.2 注水井数学模型

为方便求解，将油水两相区剖分为N个小圆环（见图2），rF为水驱前缘距离，re为油藏半径。将原来连续的饱和度分布用阶梯型的饱和度分布代替，当圆环个数趋于无限多时，阶梯型饱和度分布趋于原来连续的饱和度分布（见图3）。

图2 剖分后模型示意

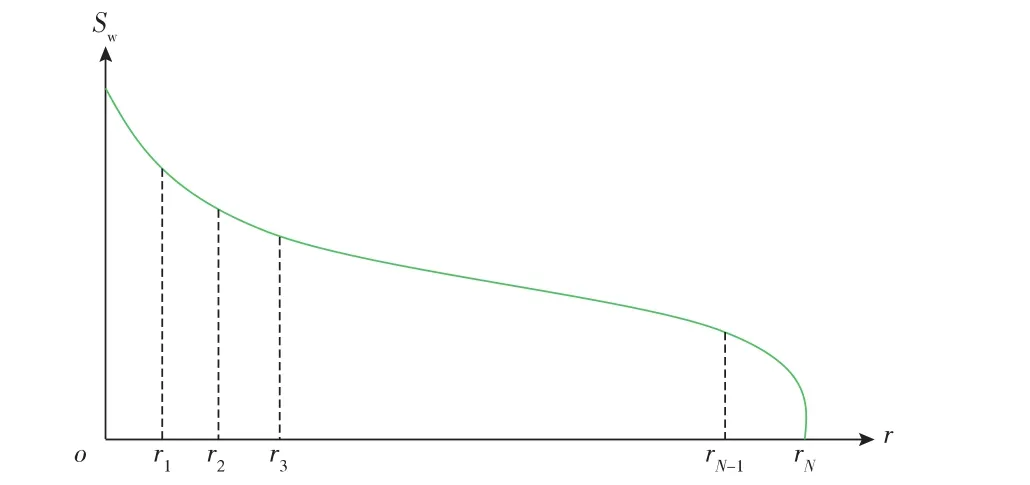
图3 饱和度分布示意

剖分后，每个圆环内的饱和度为一定值，即可认为每个圆环内的水驱油是活塞式的，每圆环内的饱和度分布由Buckley-Leverrett方程确定：

式中：rD（Sw）为 Sw对应的无因次距离；q为注水量，m3/d；tp为注水时间，h；φ 为孔隙度；h 为油藏厚度，m；rw为井半径，m；Sw为含水饱和度；f′w（Sw）为分流曲线 f′w-Sw上Sw对应的斜率。

每圆环内的饱和度为

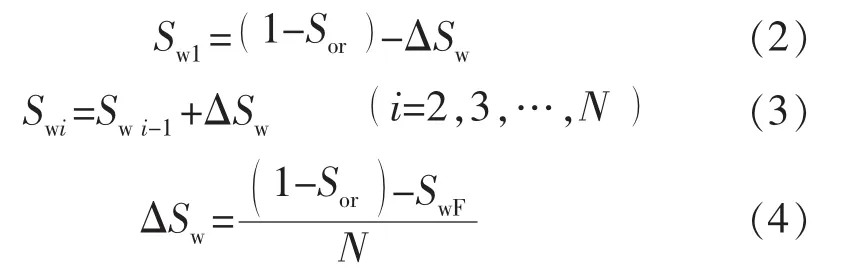
式中：Sor为残余油饱和度；SwF为水驱油前缘饱和度。

将每个圆环内的Swi代入Buckley-Leverrett方程，则可计算出每个圆环的无因次半径rDi。

对于每个圆环，其扩散方程为：

1）裂缝系统

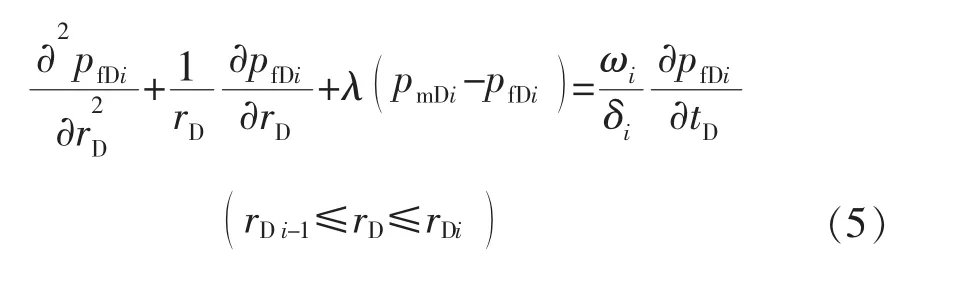
2）基质系统

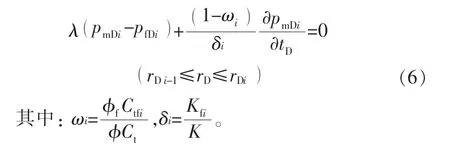
式中：pfD为无因次裂缝系统压力；pmD为无因次基质系统压力；λ为窜流系数；tD为无因次时间；φf为裂缝孔隙度；φ为地层孔隙度；Ctf为裂缝系统压缩系数,1/MPa；Ct为地层综合压缩系数，1/MPa；Kf为裂缝渗透率，μm2；K为地层平均渗透率，μm2；下标m，f，D分别表示基质、裂缝、无因次。

3）初始条件

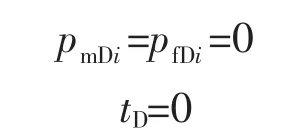
4）内边界条件

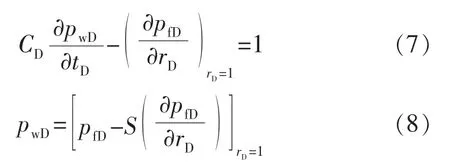
式中：CD为无因次井筒储存系数；pwD为无因次井底压力；S为表皮系数。

5）外边界条件

式中：re为油藏半径，m；μ 为流体黏度 mPa·s；B 为体积系数；pi为原始地层压力，MPa。

1.3 数学模型的求解

定义拉普拉斯变换：

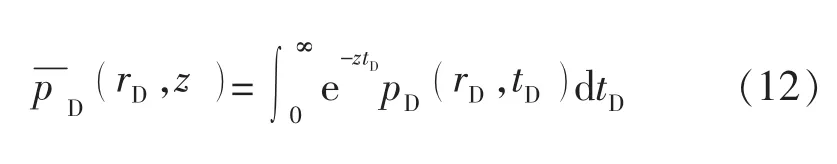
式中：z为Laplace变量。

则数学模型可转化为：

1）裂缝系统

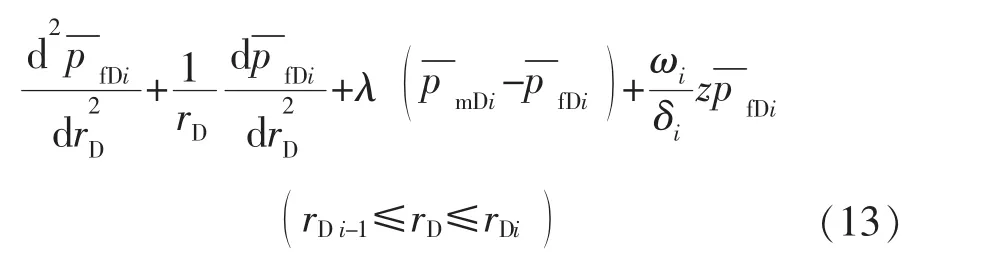
2）基质系统

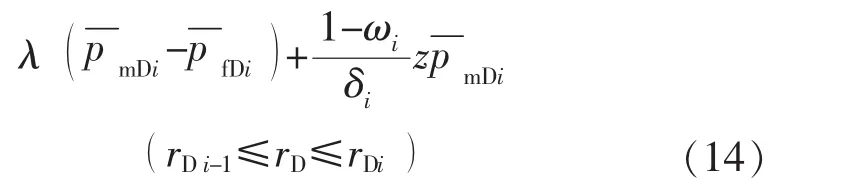
整理得：

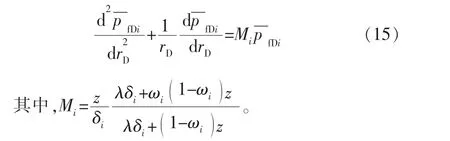
3）内边界条件

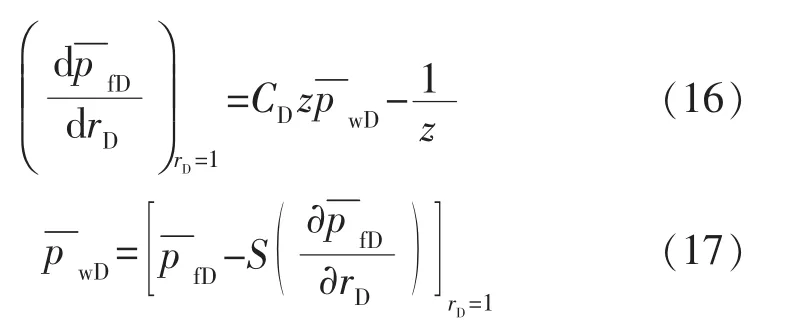
4）衔接条件

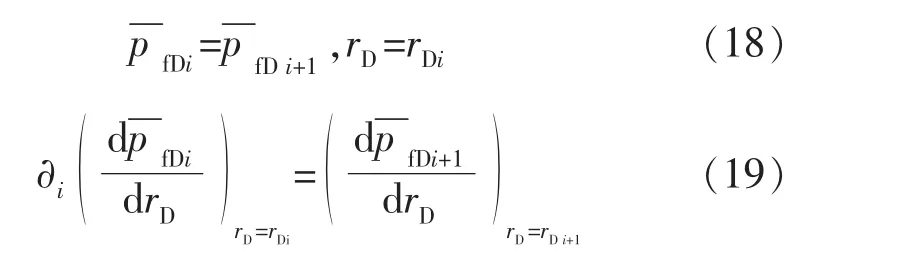
5）外边界条件

对于上述数学模型，其方程为一组0阶的虚宗量Bessel方程，通解为

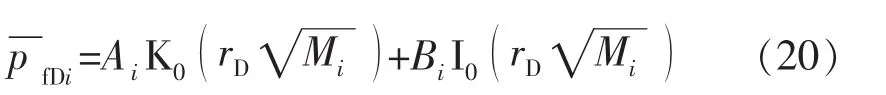
式中：I0，K0分别为第1类和第2类0阶修正Bessel函数；Ai，Bi为待定常数。

对于N个圆环，共有2N个未知数Ai，Bi。N-1个界面提供了2N-2个方程，再加上内、外边界条件，共有2N个方程，可确定2N个未知数。使用Gauss消元法［7-8］解出未知数 Ai，Bi。 根据式（16）、式（17）计算出Laplace空间下无因次井底压力的解。借助Stehfest拉普拉斯数值反演变换算法，最终可以求得实空间内无因次井底压力pwD。Stehfest拉普拉斯数值反演变换算法［9］为

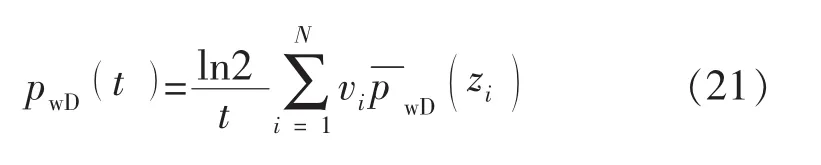
其中

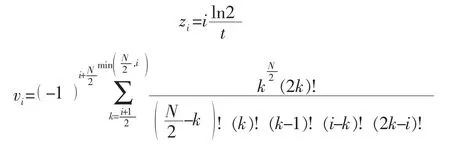
2 典型试井曲线图版分析

通过对数学模型求解，可以获得无因次井底压力与无因次时间的关系。假设关井测试阶段，水驱前缘不再发生变化，利用叠加原理得到关井阶段的压力降落解为

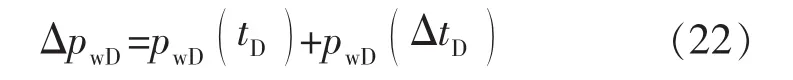
利用无因次压力降落解，可获得注水井的压力降落典型图版（见图4）。根据导数曲线特征可划分7个流动段：井筒储集效应阶段、表皮效应阶段、基质向裂缝窜流阶段、水区径向流阶段、油水两相区响应阶段、总系统径向流阶段和边界响应阶段（分别对应图4中的①—⑦）。从双对数曲线图版中可看出，在窜流阶段结束后出现第1条水平直线段，表征的是井周围水区响应，之后由于油水流度的差异，压力导数曲线呈逐渐上翘的特征，反映的是油水两相区的响应，并且油水黏度差异越大，两相区双对数曲线上翘幅度越大 （见图5），因而在试井解释时，应区别储层物性变化或不渗透边界造成的压力导数曲线上翘。在到达水驱前缘后，导数曲线上出现一个凸起，接着导数曲线出现第2条水平直线段，反映油区的压力响应特征。

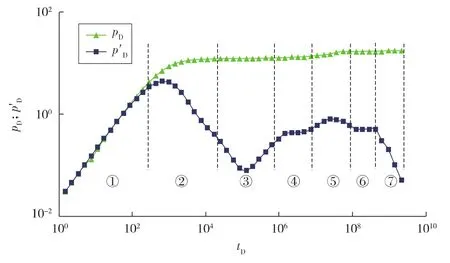
图4 裂缝性油藏注水井压力降落典型曲线

3 应用实例

M油田X井为一口注水井，在进行压力降落测试前，平均日注水350 m3，注水5个月，累计注水5.25×104m3。注水井和油藏参数见表1，地层流体的相对渗透率数据见表2。

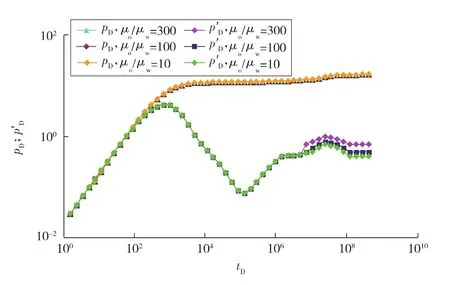
图5 油水黏度差异对双对数曲线的影响

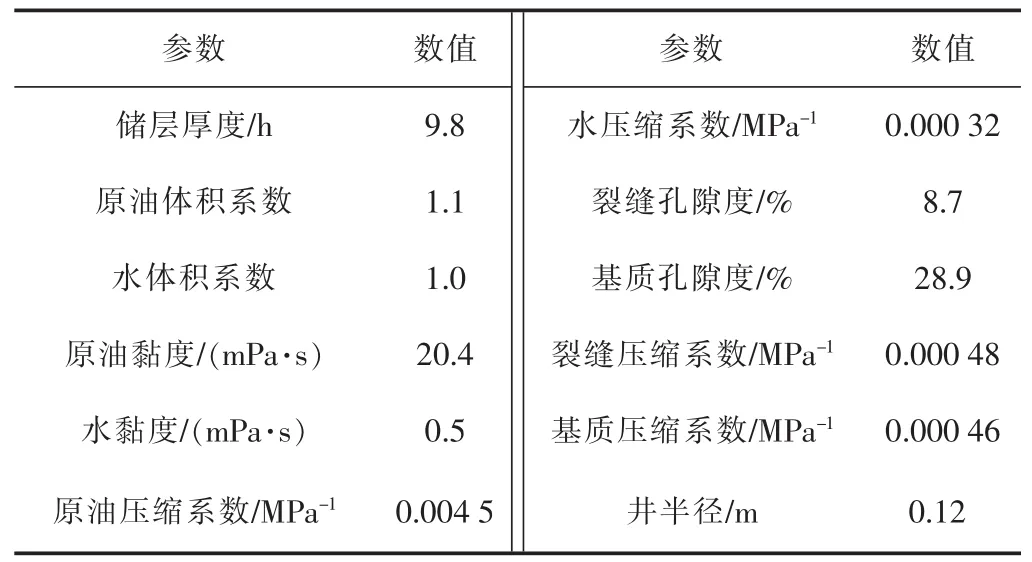
表1 油藏和井的基本参数

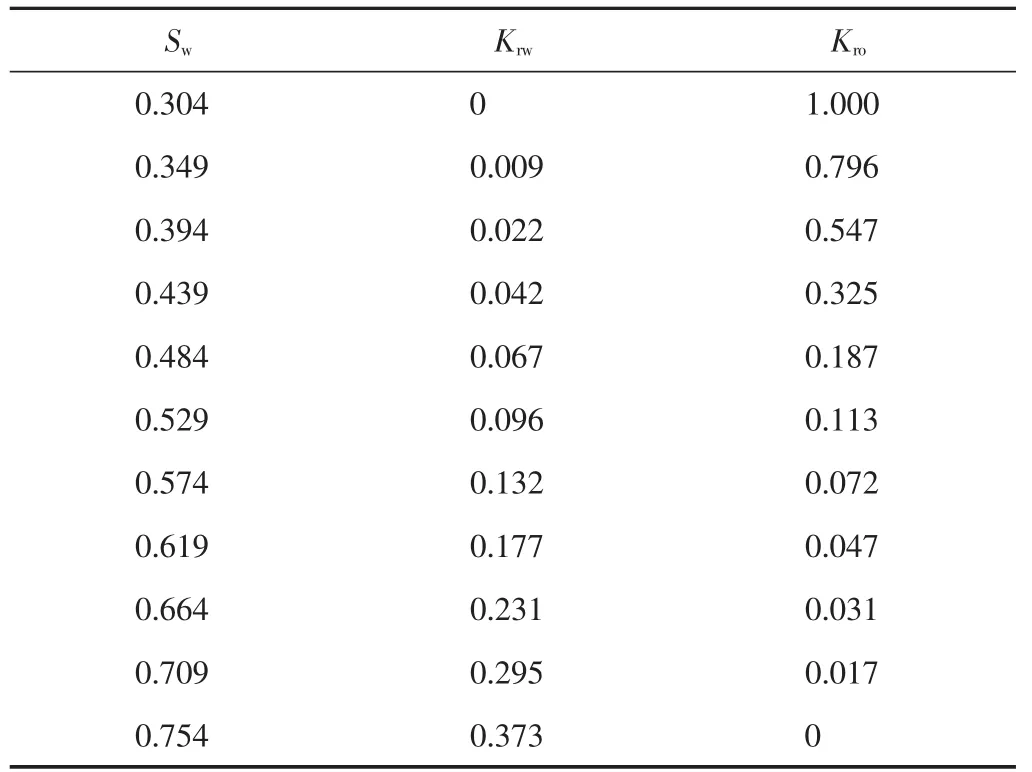
表2 地层相对渗透率数据

实测压力数据与典型图版拟合见图6，实际曲线与典型曲线的拟合步骤与油井的典型曲线拟合步骤一样［10］。根据压力拟合，可计算出残余油饱和度下的水相渗透率，根据时间拟合，可计算前缘位置［10］。实例解释参数见表3。

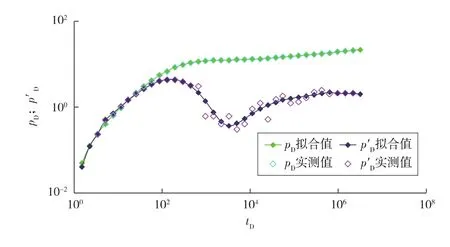
图6 压力降落曲线与典型曲线拟合图版

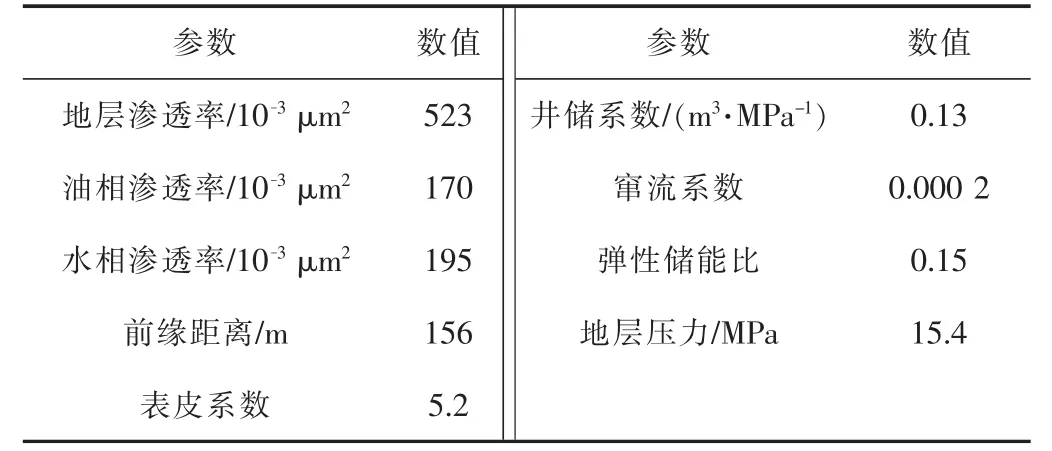
表3 实例解释结果

4 结论

1）结合裂缝性油藏渗流特征，基于Buckley-Leverrett饱和度分布方程，建立了注水井压降试井解释模型，在Laplace空间求得解析解，并采用Stehfest数值反演求得真实空间的解，绘制了裂缝性油藏注水井压降试井典型曲线拟合图版。

2）对于原油黏度较高的油藏，两相区对注水井压力响应特征较大，油水黏度差异会导致双对数曲线上翘，在试井解释时应区别储层物性变化或不渗透边界造成的压力导数曲线上翘。

3）建立的试井解释模型可计算注水前缘位置，分析注水井周围地层信息及边界情况，解释图版拟合结果与现场测试数据吻合较好，解释所得的储层参数合理可靠，对评价注水井的动态、注水开发油田注水井方案的设计具有重要的指导意义。

［1］ 尹洪军，付春权，万贵春，等.多重复合低渗透油藏注水井压力动态分析［J］.石油学报，2002，23（4）：70-74.

［2］ 刘佳洁，孟英峰，李皋，等.三区流体复合注水井试井模型研究［J］.石油天然气学报，2013，35（2）：120-125.

［3］ 巨亚锋.低渗两区复合油藏注水井试井解释模型［J］.石油天然气学报，2012，34（7）：109-113.

［4］ 李乃华.多层定压边界灌注井数学模型［J］.河北工业大学学报，2006，35（5）：32-35.

［5］ 尹洪军.合理利用典型曲线分析注水井试井资料的方法［J］.大庆石油学院学报，1993，17（2）：112-114.

［6］ 刘佳洁，孟英峰.基于油水两相渗流的地层流体复合注水井试井模型［J］.石油天然气学报，2014，36（2）：128-132.

［7］ 贾永禄，聂仁仕，王永恒，等.二次梯度非线性渗流问题求解［J］.石油天然气学报，2008，30（4）：119-122.

［8］ 刘永良，刘彬，刘大伟，等.三重介质气藏单井生产动态分析模型研究［J］.江汉石油学院学报，2001，33（2）：123-127.

［9］ 贾永禄，赵必荣.拉普拉斯变换及数值反演在试井分析中的应用［J］.天然气工业，1992，12（1）：60-64.

［10］张艳玉，姚军.现代试井解释原理与方法［M］.北京：中国石油大学出版社，2006：127-128.

（编辑 孙薇）

Interpretation method and application for pressure fall-off test of water injection well in fractured reservoir

JIANG Yong,ZHANG Lei,BIE Xuwei,WANG Di,HUANG Lei
(Tianjin Branch of CNOOC Ltd.,Tianjin 300452,China)

In order to describe the fractured reservoir dynamic characteristics of injection well more accurately and get more reliable information about formation and test wells,the interpretation model for pressure fall-off test of water injection well was presented and numerically solved by Buckley-Leverrett saturation,and typical fitting chart was obtained.According to the characteristics of pressure fall-off curve,seven distinct flow phases can be divided:wellbore storage effect,skin effect,matrix crack channeling,water radial flow,response of oil-water,radial flow of total system,and boundary response phases.The viscosity difference between oil and water would lead to the upward of the double logarithmic curve.The model can be used for calculating the position of the injection front,and analyzing the stratigraphic information and boundary conditions around the injection wells.The research results provide a practical reference for the dynamic evaluation and design of injection wells.

fractured reservoir;water injection well;well test;mathematical model

TE357.6+2

A

国家自然科学基金项目“储层裂缝形成机理”（40772089）

10.6056/dkyqt201704028

2016-12-20；改回日期：2017-05-10。

姜永，男，1985年生，工程师，硕士，主要从事试井、油藏工程方面的研究工作。E-mail：jiangyong198786858@163.com。

姜永，张雷，别旭伟，等.裂缝性油藏注水井压降试井解释方法及应用［J］.断块油气田，2017，24（4）：565-569.

JIANG Yong，ZHANG Lei，BIE Xuwei，et al.Interpretation method and application for pressure fall-off test of water injection well in fractured reservoir［J］.Fault-Block Oil&Gas Field， 2017， 24（4）：565-569.