分形拟三重介质致密油藏产能预测模型

刘化普，刘慧卿，王敬，彭永灿，高阳，李映艳

（1.中国石油大学（北京）石油工程教育部重点实验室，北京 102249；2.中国石油新疆油田分公司勘探开发研究院，新疆 克拉玛依 834000）

分形拟三重介质致密油藏产能预测模型

刘化普1，刘慧卿1，王敬1，彭永灿2，高阳2，李映艳2

（1.中国石油大学（北京）石油工程教育部重点实验室，北京 102249；2.中国石油新疆油田分公司勘探开发研究院，新疆 克拉玛依 834000）

致密油藏渗流机理复杂、产能预测难度大。文中引入分形理论，推导出基质、天然微裂缝、人工裂缝的分形孔隙度和分形表观渗透率。建立了考虑启动压力梯度及压敏效应的分形拟三重介质致密油藏数学模型，推导出模型压力解与动态供给边界的变化情况。在此基础上，建立了产能预测模型，结合实例数据完成模型验证，进行供给半径和产能的动态预测，并对非线性渗流参数进行敏感性分析。结果表明：供给半径随时间非线性增加，同一时刻，启动压力梯度及分形系数越大，供给半径越小；分形致密油藏产能受非线性渗流参数的影响，启动压力梯度越低，变形系数越小，分形系数越小，则日产量越高，反之日产量越低。

致密油；分形；三重介质；基质；裂缝；产能模型

0 引言

天然微裂缝发育的致密油藏具有低孔、低渗、低产能的特性，地层原油在流动过程中不遵循达西定律，具有一定的启动压力梯度。此外，由于裂缝发育，压敏效应也比较明显［1-3］。致密油藏多采用体积压裂方式开发生产［4］，经过体积压裂，形成人工裂缝、天然微裂缝、基质拟三重介质（区别于孔洞缝三重介质）。由于致密油藏内部孔隙结构复杂，又有启动压力梯度及应力敏感效应等非达西因子的影响，因此，对于致密油藏渗流机理与产能预测的研究比较困难。为了探究这些规律，国内外很多专家学者在欧式几何基础上提出了不同产能预测模型［5-9］。然而实际地层中裂缝分布复杂，欧式几何空间难以描述裂缝实际分布情况，而分形理论恰好能对不规则、不均匀的复杂系统进行比较精确的描述。自1979年Mandelbrot等［10］首次提出分形概念以来，分形理论便被运用到描述复杂物体当中，且取得较大进展。后来，很多学者将分形理论引入到渗流力学当中，建立分形渗流模型，分析渗流特征［11-14］。因此，本文引入分形理论，建立了基质-天然微裂缝-人工裂缝分形拟三重介质模型，并在此基础之上推导出体积压裂水平井产能预测模型。通过与实际生产数据对比，证明了模型的正确性，进而实现对致密油藏的产能预测。

1 拟三重介质致密油藏分形模型

研究表明，岩石、土壤等真实多孔介质在一定尺度范围内都具有分形特征，分形多孔介质的管径及迂曲度满足分形标度率［15-16］。

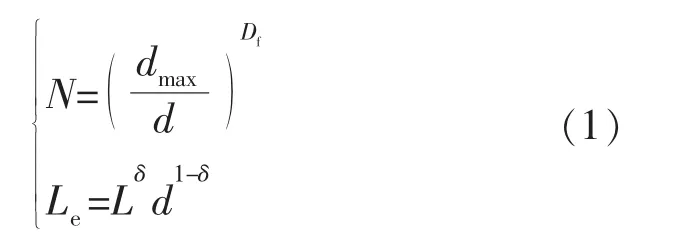
1.1 基质孔隙系统

基质系统采用分形迂曲毛束管模型，模型由一束不同直径的弯曲毛细管组成，任意2根毛细管间彼此独立，弯曲毛细管的直径与迂曲度满足分形标度率。

通过对单位分形集内孔隙进行积分运算，可得基质系统分形孔隙度φm的表达式：

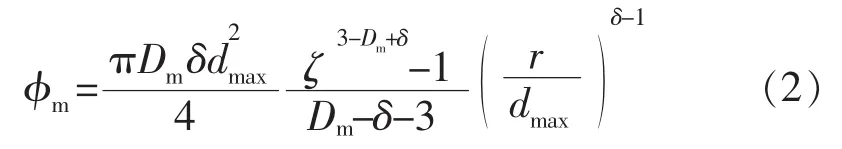
结合 Hagen-Poiseuille 方程，并根据 Carman［17］对弯曲管束的修正公式，可进一步得到基质系统分形表观渗透率Km的表达式：

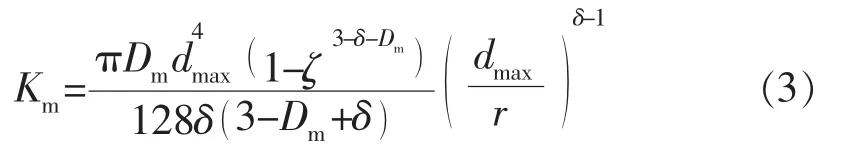
1.2 天然微裂缝系统

天然微裂缝系统采用分形面缝模型，裂缝宽度与迂曲度满足分形标度率。

通过对单位分形集内裂缝进行积分运算，可得裂缝系统分形孔隙度φf的表达式：

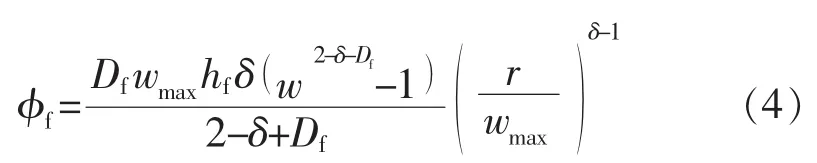
结合基质系统的推导过程，同理可得天然微裂缝系统分形表观渗透率Kf的表达式：

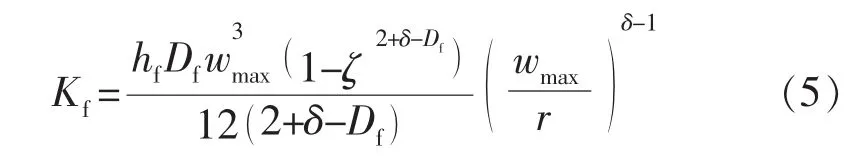
1.3 人工裂缝系统

对于致密油藏，基质、天然微裂缝、人工裂缝拟三重介质构成连通的网络结构，从而获得经济产能。由于人工裂缝形态复杂，为了简化计算，同时又能尽量符合人工裂缝真实形态，在结合天然微裂缝分形面缝模型的基础上，本文提出分形面缝二叉树模型描述人工裂缝系统分形特征。假设一条二叉树面缝有k级分级，每级裂缝的缝高都为hf，任意相邻2级裂缝间缝宽满足等比级差：

由此可推导出人工裂缝系统分形孔隙度φF的表达式：

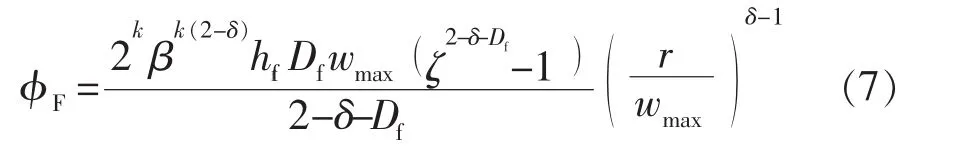
结合基质系统推导过程，进一步可得人工裂缝系统分形表观渗透率KF的表达式：

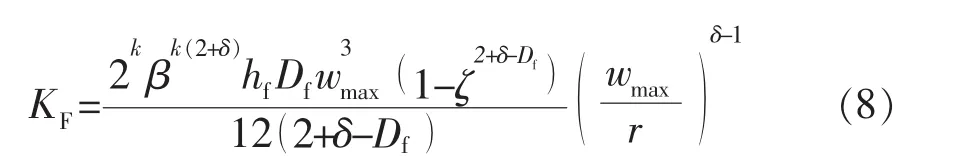
2 分形拟三重介质致密油藏数学模型

2.1 概念模型

用分形表观渗透率与分形孔隙度分别修正基质、天然微裂缝、人工裂缝的渗透率与孔隙度，模型其他假设条件为：1）致密油藏地层水平、等厚，横向无限大；2）致密油藏基质与天然微裂缝作为“源”，基质中的流体流向天然微裂缝，天然微裂缝流向人工裂缝，只有人工裂缝中的流体流向井筒；3）不考虑重力与毛细管力的影响；4）单相微可压缩流体，考虑启动压力梯度与应力敏感性，不考虑温度的变化。

2.2 数学模型

引入拟压力函数，表征应力敏感效应：

由此得到考虑启动压力梯度及应力敏感效应的分形拟三重介质致密油藏数学模型：

2.3 数学模型求解

通过对数学模型进行Laplace变换，结合Besself方程及格林函数，从而得到Laplace空间考虑启动压力梯度及应力敏感效应的压力解：

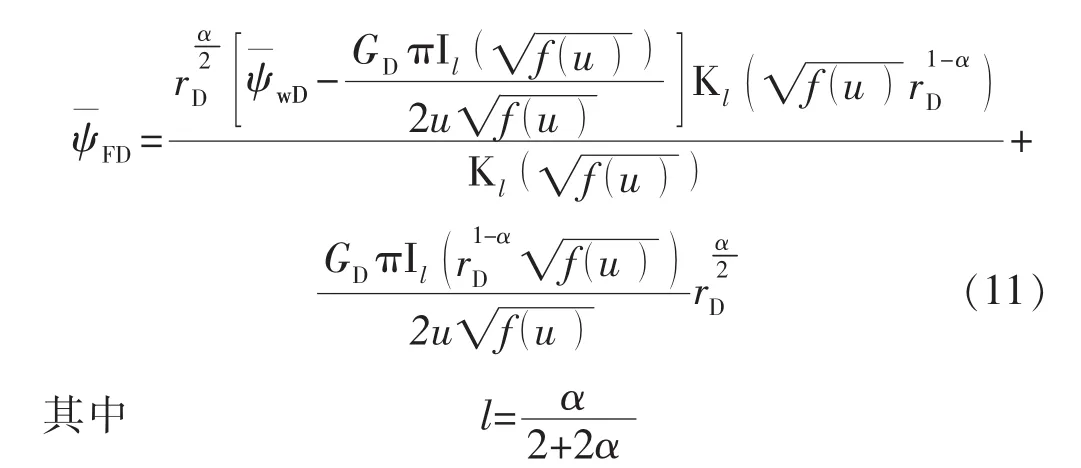
给定tD，reD，按式（11）所得的解析解进行Stefhest数值反演，从而得到无因次拟压力ψFD（tD，reD）。若此压力低于无因次启动压力，减小reD，否则增大reD，从而通过迭代法获得供给边界随时间的变化情况。

3 分形拟三重介质致密油藏产能模型

假设经过体积压裂形成椭圆形的缝网，对于单根主裂缝所控制的渗流场可分为4个区，即主裂缝区、分形人工裂缝控制区、分形天然微裂缝控制区和基质区。

3.1 主裂缝区

主裂缝渗透率较高，流体沿主裂缝呈线性流动，由此得到主裂缝区产能预测公式：

3.2 人工裂缝控制区

人工裂缝控制区可将主裂缝简化为线源，流体在人工裂缝控制区内将发生二维非达西椭圆渗流［18］。引入椭圆坐标 （ξ，η），考虑启动压力梯度及应力敏感效应，由此可以得到人工裂缝控制区产能预测公式：

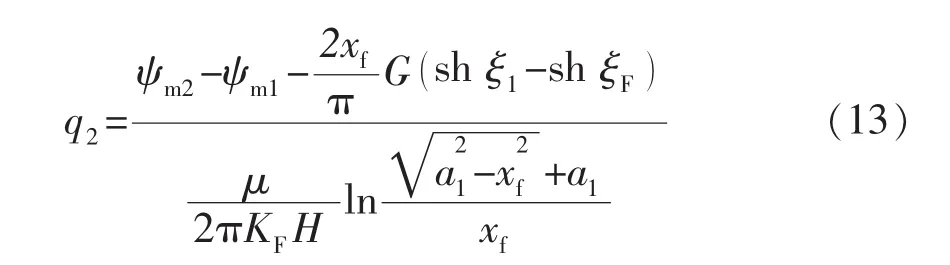
3.3 天然微裂缝控制区

结合人工裂缝简化条件，容易得到考虑启动压力梯度及应力敏感效应的天然微裂缝区产能预测公式：

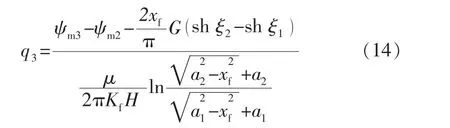
3.4 基质控制区

随着裂缝内原油逐渐被开采出来，裂缝区压力下降，基质内流体开始向裂缝区窜流。基质内流体流动表现为低速非达西渗流，由此得到基质控制区的产能预测公式：

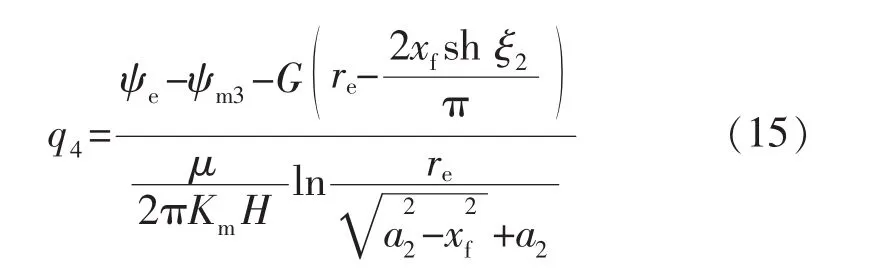
3.5 单井产能模型

根据等值渗流原理，假设第i条主裂缝受相邻裂缝的干扰面积为Si，由此可得到单根压裂主裂缝产能预测公式：

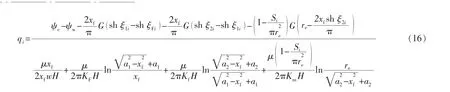
假设压裂后形成n条主裂缝，由此可得到致密油藏体积压裂水平井产能模型：

4 应用实例分析

运用所得到的产能模型，进行现场实例拟合，从而验证模型的正确性，再进一步进行产能与供给边界预测。算例中致密油藏JHW019井基本参数见表1。

表1 致密油藏基础参数

4.1 致密油藏产能预测

运用本文所推导的产能模型，结合算例中致密油藏的基本参数，进行历史拟合，并对JHW019井进行产能预测，结果见图1。从图可以看出：本文推导的分形拟三重介质致密油藏产能模型计算值与实际值拟合程度较高；致密油藏开发初始阶段产能下降较快，之后逐渐趋于平稳，稳产后日产油量约3 t。

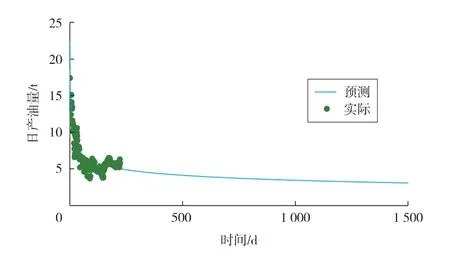
图1 JHW019井产量预测

4.2 致密油藏供给边界预测

结合算例中基本参数，通过Stehfest数值反演及牛顿迭代，借助Matlab编程，可以得到分形拟三重介质致密油藏在不同启动压力梯度及分形系数下，供给半径随时间的变化曲线（见图2）。由图可知：供给半径随时间的增加呈非线性增加。初始阶段，供给半径增加较快，随着时间的增加，供给半径增加幅度逐渐变缓，这是由于初始阶段主要是裂缝区参与渗流，压力波传播速度快，经过一段时间后，压力波在基质中传播，供给半径增加幅度下降。启动压力梯度及分形系数越大，曲线位置越往下，同一时刻，供给半径越小。其中：随着启动压力梯度等间距增大，供给半径下降幅度逐渐减小；而随着分形系数的增大，供给半径下降幅度变化不明显——说明了启动压力梯度相对分形系数有更强的敏感性。

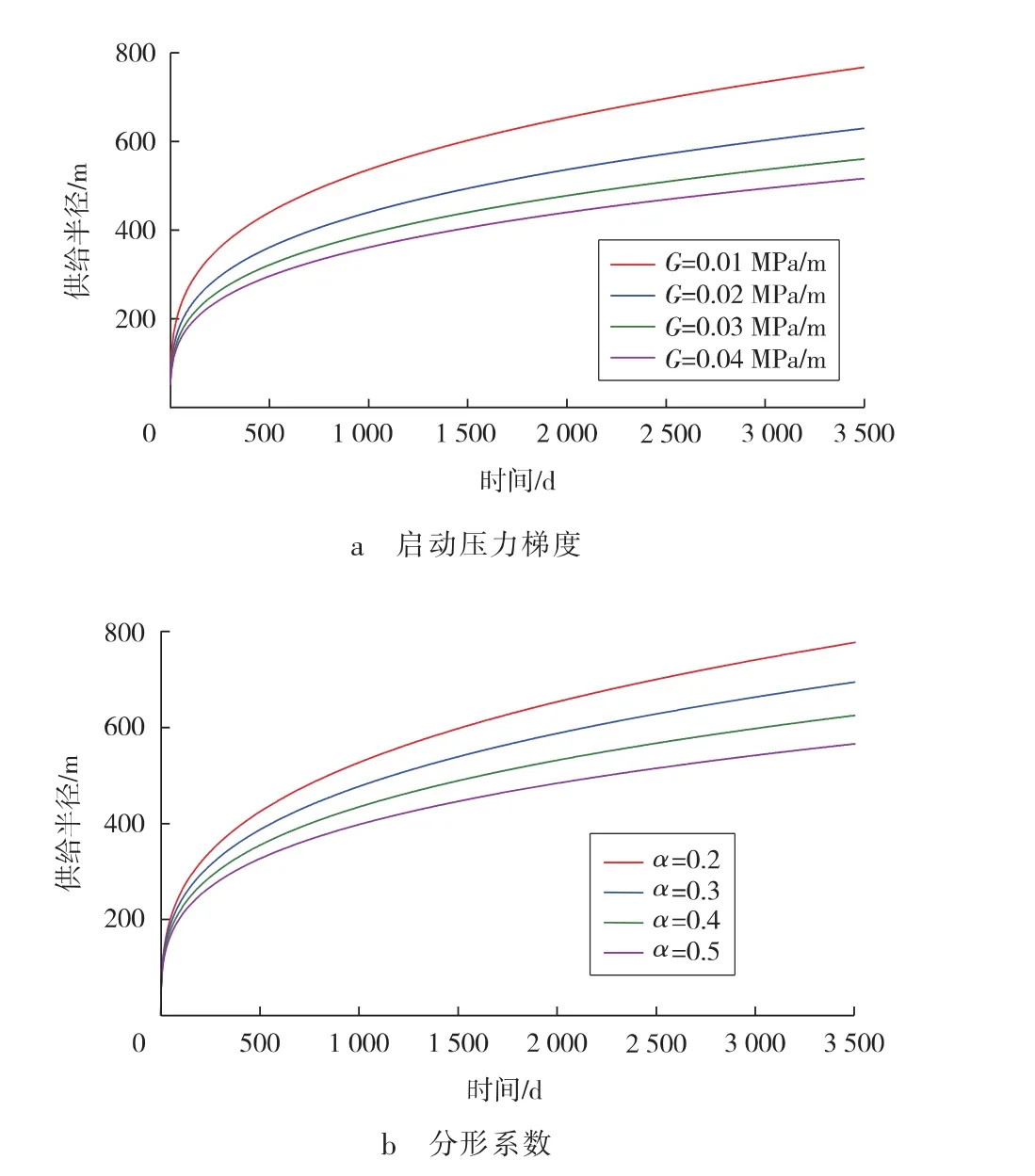
图2 不同非线性参数下供给半径随时间的变化

4.3 非线性渗流参数敏感性分析

分形拟三重介质致密油藏产能受到启动压力梯度、压敏效应、分形系数等非线性参数的影响，因此，本文分别对启动压力梯度、变形系数及分形系数进行敏感性分析，结果见图3。由图3a可以看出，启动压力梯度越大，初期产能下降越快，总体产能越低。由图3b可以看出：开发初期，压敏效应作用明显，产能递减快；变形系数越大，日产油量越低，但是整个曲线的递减趋势是相同的。由图3c可以看出：分形系数越大，单位分形集内裂缝与孔隙迂曲程度越大，致密油藏渗流阻力增大，物性变差，产能下降；分形系数越大，日产油量越低，但是分形系数只影响产量的相对高低，并不影响产量递减的趋势。

5 结论

1）运用分形理论，推导出分形孔隙度及分形表观渗透率表达式，建立考虑启动压力梯度及应力敏感效应的分形拟三重介质致密油藏数学模型，并通过Laplace变换、Stehfest数值反演及牛顿迭代的方法得到供给半径变化情况。所建立的分形拟三重介质致密油藏产能预测模型计算值与实际值拟合程度较高，可以用于致密油藏的供给半径及产能预测。

2）致密油藏的供给半径随时间非线性增加，同一时刻，启动压力梯度及分形系数越大，供给半径越小；启动压力梯度、变形系数及分形系数均会影响分形致密油藏的产能，启动压力梯度越低、变形系数及分形系数越小，日产油量越高，反之越低。

3）分形理论能够较精确地描述不规则、不均匀的物体，对于孔隙结构复杂的致密油藏，运用分形理论进行渗流规律分析及产能预测将得到更深入的研究。

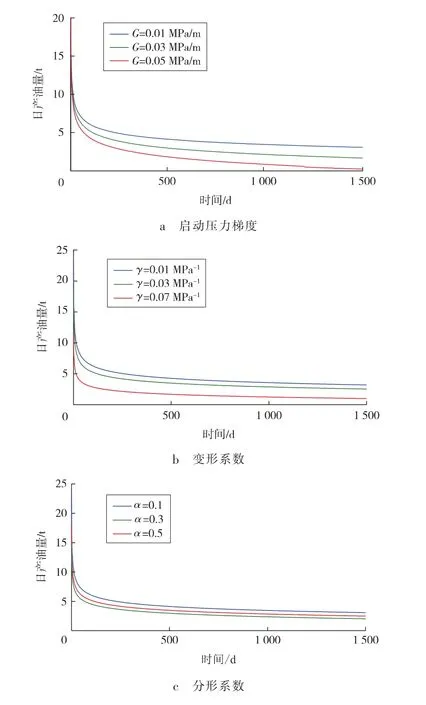
图3 不同非线性参数敏感性分析

6 符号注释

N为弯曲毛细管数目；d，dmax分别为毛细管管径、最大毛细管管径，m；L，Le分别为毛细管表观长度、毛细管实际长度，m；δ为迂曲分形维数；Dm，Df分别为基质管径、裂缝缝宽分形维数；ζ为最小孔道直径与最大孔道直径之比；r，rw，re分别为渗流半径、井筒半径、供给边界半径，m；w，wmax分别为裂缝宽度、最大裂缝宽度，m；hf为裂缝高度，m；t为时间，s；Ct为综合压缩系数，Pa-1；为弹性储容比；α 为分形系数；λfF，λmf分别为天然微裂缝、基质窜流系数；αm，αf分别为基质、天然微裂缝形状因子，m-2；ψ，ψi，ψm1，ψm2，ψm3，ψw，ψe分别为拟压力、初始拟压力、地层与主裂缝边缘交界面处的拟压力、人工裂缝控制区边缘拟压力、天然微裂缝控制区边缘压力、井底流压、供给边缘的压力，Pa；q1，q2，q3，q4分别为主裂缝、人工裂缝、天然微裂缝、基质控制区流量，m3/s；H 为地层厚度，m；G 为启动压力梯度，Pa/m；B 为体积系数；po，p 分别为初始、目前压力，Pa；γ 为渗透率变形系数，Pa-1；u 为 Laplace 空间变量；f （u）为中间变量；为 Laplace 空间无因次拟压力；Il，Kl为 l阶贝塞尔函数；xf为裂缝半长，m；ξ1，ξ2，ξF分别为人工裂缝椭圆渗流区、天然微裂缝椭圆渗流区、地层与主裂缝边缘交界面处的椭圆坐标；a1，a2分别为人工裂缝控制区、天然微裂缝控制区椭圆长轴，m；Q为水平井产能，m3/s；下标m，f，F 分别表示基质、天然微裂缝、人工裂缝；下标j代表m，f，F；下标D表示无因次；下标i表示第i条裂缝。

［1］ LIU L F，WANG X.The moving boundary movement of vertical fractured well in tight oil reservoir［J］.Advanced Materials Research，2013，868：633-637.

［2］ 李滢，杨胜来，任双双，等.致密油储层基质块渗流特征［J］.断块油气田，2016，23（3）：342-345.

［3］ YUAN B，SU Y，MOGHANLOO R G，et al.A new analytical multi-linear solution for gas flow toward fractured horizontal wells with different fracture intensity ［J］.Journal of Natural Gas Science&Engineering，2015，23：227-238.

［4］ 闵春佳，卢双舫，唐明明，等.致密油储层水平井压裂参数优化模拟［J］.断块油气田，2015，22（6）：794-797.

［5］ 魏漪，冉启全，童敏，等.致密油压裂水平井全周期产能预测模型［J］.西南石油大学学报（自然科学版），2016，38（1）：99-106.

［6］ 史晓东.非均质致密油储层水平井体积压裂产能预测［J］.特种油气藏，2016，23（3）：90-93.

［7］ RAGHAVAN R S，CHEN C C，BIJAN A.An analysis of horizontal wells Intercepted by multiple fractures［J］.SPE Journal，1997，2（3）：235-245.

［8］ KUPPE F，SETTARIA.A practicalmethod fortheoretically determining the productivity of multi-fractured horizontal wells［J］.Journal of Canadian Petroleum Technology，1998，37（10）：68-81.

［9］ 石磊，匡建超，曾剑毅，等.川西新场气田沙溪庙组致密碎屑岩储层单井产能评价与预测［J］.石油实验地质，2009，31（4）：338-342.

［10］ MANDELBROT B B， NESS J W V.Fractional brownian motions，fractional noises and applications［J］.Siam Review，2006，10（4）：422-437.

［11］ CHANG J，YORTSOS Y C.Pressure-transient analysis of fractal reservoirs［J］.SPE Reservoir Evaluation&Engineering，1990，5（1）：31-38.

［12］ ACUNA J A，YORTSOS Y C.Application of fractal geometry to the study of networks of fractures and their pressure transient［J］.Water Resources Research，1995，31（3）：527-540.

［13］ CHANG J，YORTSOS Y C.A note on pressure-transient analysis of fractal reservoirs［J］.British Journal of Sports Medicine，1993，1（2）：380-386.

［14］孔祥言，李道伦，卢德唐.形渗流基本公式及分形油藏样板曲线［J］.西安石油大学学报（自然科学版），2007，22（2）：1-5.

［15］ YU B，CHENG P.A fractal permeability model for bi-dispersed porous media［J］.International Journal of Heat&Mass Transfer，2002，45（14）：2983-2993.

［16］ YU B.Analysis of flow in fractal porous media［J］.Applied Mechanics Reviews，2008，61（5）：1239-1249.

［17］ CARMAN P C.Fluid flow through granular beds［J］.Chemical Engineering Research&Design，1937，75（1）：S32-S48.

［18］郝明强，王晓冬，胡永乐.压敏性特低渗透油藏压裂水平井产能计算［J］.中国石油大学学报（自然科学版），2011，35（6）：99-104.

（编辑 史晓贞）

Productivity prediction model of fractal pseudo-triple medium tight oil reservoirs

LIU Huapu1,LIU Huiqing1,WANG Jing1,PENG Yongcan2,GAO Yang2,LI Yingyan2
(1.MOE Key Laboratory of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;2.Research Institute of Exploration and Development,Xinjiang Oilfield Company,PetroChina,Karamay 834000,China)

In tight oil reservoir,it is difficult to study the percolation mechanism and productivity prediction.However,fractal theory provides a method to describe the complex system.Therefore,this paper introduces the fractal theory to deduce matrix,natural micro fractures,artificial fractures′fractal fracture porosity and fractal apparent permeability.The mathematical model of the pseudo-triple medium tight oil reservoir with the starting pressure gradient and the stress sensitive effect was established.The pressure solution of the model and the change of the radius of the oil discharge were derived.On the basis of the above,the productivity prediction model was established.Combined with the field data,the fractal model presented in this paper was verified.After that,supply radius and production were predicted.Finally,nonlinear parameter sensitivity analysis was conducted.The results show that with the increase of time,the supply radius increases nonlinearly.At the same time,the larger the starting pressure gradient and fractal coefficient are,the smaller the supply radius is;nonlinear parameters have a great effect on production of fractal tight oil reservoirs.The lower the starting pressure gradient is,the smaller the deformation coefficient is;the smaller the fractal coefficient is,and the higher the daily output is.

tight oil;fractal;triple medium;matrix;fracture;productivity model

TE319

A

国家重点基础研究发展计划（973计划）项目“典型致密油藏开发系统优化研究”（2015CB250906）

10.6056/dkyqt201704022

2017-01-27；改回日期：2017-05-15。

刘化普，男，1993年生，在读硕士研究生，研究方向为油藏数值模拟与提高采收率。E-mail：liuhuapu@foxmail.com。

刘化普，刘慧卿，王敬，等.分形拟三重介质致密油藏产能预测模型［J］.断块油气田，2017，24（4）：536-540，556.

LIU Huapu，LIU Huiqing，WANG Jing，et al.Productivity prediction model of fractal pseudo-triple medium tight oil reservoirs［J］.Fault-Block Oil&Gas Field，2017，24（4）：536-540，556.