多点地质统计学算法Snesim参数敏感性分析

王红，李少华

（长江大学地球科学学院，湖北 武汉 430100）

多点地质统计学算法Snesim参数敏感性分析

王红，李少华

（长江大学地球科学学院，湖北 武汉 430100）

Snesim是第一个被应用到油田储层建模中的多点地质统计学算法。文中以弯曲河道作训练图像，对该算法建模过程中常涉及到的参数（如目标边际分布与伺服系统参数、搜索半径与搜索角、旋转角与仿射率，以及多重网格层数等）进行敏感性分析。分析结果表明：当目标相比例值与训练图像边际概率值接近时，模拟结果较合理；增大伺服系统参数可使模拟结果的边际概率接近目标相比例，但伺服系统参数设置过高将降低河道连续性；搜索邻域应与模拟维度相适应；局部旋转角和仿射率可将训练图像中的平稳与非平稳信息融合起来，用于趋势模拟；多重网格模拟中，网格层数取决于最大尺度结构信息的大小。以上认识可为利用Snesim算法进行储层建模提供一定的指导。

多点地质统计学；Snesim算法；储层建模；参数敏感性分析

0 引言

多点地质统计学是相对于两点地质统计学而提出的［1-3］。其模拟结合了基于象元和基于目标方法的优势，能精确地表征储层复杂的空间构型和几何形态，且容易满足条件数据，现已越来越多地被应用到地质情况复杂的储层建模中［4-7］。

Snesim（Single normal equation simulation）算法是Strebelle和Journel提出的一种多点地质统计学建模方法［8-9］。鉴于Snesim算法需要训练图像作为结构特征的描述，以及数据样板作为参数估计的基本载体，该算法参数的类型和功能与传统两点地质统计学算法相比有很大不同。Snesim算法常用输入参数，如目标边际分布与伺服系统参数、搜索半径与搜索角、旋转角与仿射率，以及多重网格层数等，需要在理解其原理和功能的基础上进行敏感性分析，对比参数控制下的模拟结果，以说明其对最终实现的影响。笔者采用参数敏感性分析与模拟结果对比的方法，在理解Snesim算法原理的基础上，探讨了以上算法参数的最佳设定原则，给出了合理的参数设置建议，以期更好地应用该算法指导建模。

1 Snesim基本原理

多点地质统计学方法的核心分为三部分：训练图像、数据事件、多点概率［10］。训练图像即特定的定量储层地质模式，数据事件即特定的多点空间结构模式，多点概率即数据事件在训练图像中出现的频率。其模拟的基本思路为：通过数据样板扫描训练图像建立多点统计概率，利用获得的多点统计概率，进行未知节点处概率模拟。Snesim在进行概率估计的时候，相对于两点统计，不再用一组方程进行概率估计，而是仅用一个平衡方程式［11］。Snesim应用“搜索树”一次性存储训练图像的条件概率分布，并保证在模拟过程中快速提取条件概率分布函数，大大缩短了运算时间，使多点地质统计学储层建模真正意义上的推广成为可能。多点地质统计学技术已经在河流相、滨海相及三角洲前缘微相储层得到了很好的应用［12-15］。

Snesim模拟算法的实施步骤为：1）扫描训练图像，建立搜索树。2）条件数据分配到最邻近的网格，定义随机访问路径。3）在每一个未知节点μ，保留包含在最大数据样板内的条件数据。从搜索树里提取多点概率分布，计算局部条件概率，建立未知节点局部条件概率分布。4）利用蒙特卡洛抽样决定未知节点的值，并将实现值加入到条件数据中。5）重复步骤3）和4），直到所有未取样网格都访问到。

2 主要参数说明及敏感性分析

在了解Snesim算法流程的基础上，分别对目标边际分布与伺服系统参数、搜索样板半径及搜索角、旋转角与仿射率，以及多重网格层数的功能进行详细阐释，对各个参数进行敏感性分析，并对模拟结果进行分析和对比，以给出合理的设置建议。

2.1 目标边际分布与伺服系统参数

在Snesim算法中用训练图像代表先验地质信息（见图1），它为序贯模拟提供了“模式信息”。用P（A）表示训练图像的边际概率，以P*（A）表示目标相比例。在实际应用中，当 P（A)与 P*（A）差别很大时，P*（A）便无法准确再现。解决这个问题需要用到伺服系统校正，在从一个节点到另一个节点的模拟过程中，伺服系统校正使得正在运行的边际概率趋近目标相比例。

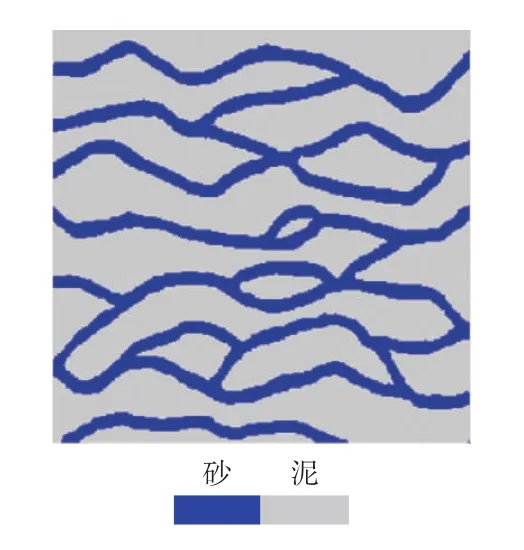
图1 弯曲河道训练图像

伺服系统控制参数的校正原理为：首先使用数据样板扫描训练图像获得 2个数据事件 P（A，B），P（B）（其中A表示中心节点处的相类型；B表示中心节点周围的多点数据事件）的重复次数，二者的重复次数储存在搜索树中。然后以序贯模拟的方式，每个数据事件的未知节点的概率分布函数 P（A|B），都能通过 P（A，B），P（B）重复次数的比值计算得出：

设Pc（A）为模拟未知节点前的概率分布函数，即由原始采样数据和之前所有模拟值计算出的比例。条件概率P（A|B）经由式（2）的改进可趋近目标相比例，形成新的概率分布函数：

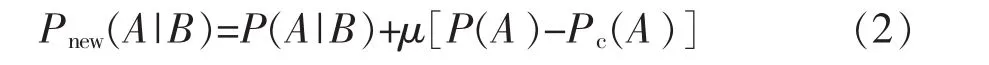
其中，μ由伺服系统参数λ计算：

λ∈［0，1）。 λ 值越大，校正幅度越大。

目标相比例与伺服系统参数相互影响。为了分析两者之间的相互作用，分别将其设定为3个不同的值，并进行敏感性分析。 P*（A）分别设定为 0.60，0.28，0.10；λ分别设定为 0，0.50，0.99。使用图 1 中 P（A）=0.28 的训练图像，得到不同 P*（A）、不同 λ 下的实现（见图 2）。其中，c为模拟河道比例。对比模拟结果可知：

1）不进行伺服系统校正时（见图 2a，2d，2g），产生的模拟河道比例与相应的目标全局概率分布函数接近。

2）通过增加伺服系统参数，可以使模拟得到的边际概率接近目标相比例，但却以牺牲相的结构信息为代价。当伺服系统参数由0增加到0.50时，模拟得到的河道比例与目标更为接近（见图2b，2e，2h）。当伺服系统参数很大时（λ=0.99），模拟得到的结果准确再现了目标相比例，但河道的曲线形态已经消失了。

3）当目标相比例与训练图像比例相同时（见图2d—2f），模拟结果中河道的连续性、宽度、弯曲程度与训练图像最接近。不同的修正概率参数下所得的结果也是相似的。

图2 目标相比例与伺服系统参数敏感性分析

4）当目标相比例与训练图像比例相差很大时（见图 2a—2c，2g—2i），河道的形态会改变。 例如：目标相比例为0.60时，模拟得到的河道会比训练图像中的宽；而当目标相比例为0.10时，河道宽度会变窄，连续性会变差。随着伺服系统参数的增加，这种情况会更加明显。

可见，边际概率P（A）与多点数据并不是相互独立的。因此，目标相比例的设置应与训练图像比例尽可能接近。当二者差别很大时，建议产生一个新的训练图像，使它的边际比例与目标相比例接近，而不是使用更高的伺服系统参数去校正。

2.2 搜索邻域

数据样板是多点模拟中的关键概念。样板的几何形状、节点数、节点的排序都影响着模拟结果。在Snesim中，数据样板由搜索椭球体参数决定，需要对搜索椭球体的搜索半径 （hx，hy，hz）和 搜索 角（angel_1，angel_2，angel_3）进行敏感性分析。

2.2.1 搜索半径

二维模型中只需考虑hx，hy。为了对比搜索半径大小对模拟结果的影响，二者分别被设定为250，100，10，有9种不同的组合形式（见图3）。当hx=hy时，模拟效果最好（见图 3a，3e，3i）；而当二者相差很大时，模拟效果最差（见图 3c，3g）。

图3 搜索半径敏感性分析

当hx=hy时，样板近似圆形，并变换尺度以适应不同的多重网格，因此图3a，3e，3i的模拟结果相近；当hx=250而hy=10时，样板变为沿长轴延伸的椭圆形，最大半径沿x轴方向，这时样板只能捕捉和再现沿x轴方向的变化；同理，当hx=10而hy=250时，样板沿y轴拉伸，只能捕捉到沿y轴的变化。此外，搜索半径应始终大于单个网格的大小。一般来说，搜索样板越大，那么模拟结果越接近合理。但由于计算量的关系，搜索样板不能无限大，一般取该区网格块大小的1/3即可［16］。测试结果表明，当结合使用多重网格模拟时，随着搜索半径的增大，模拟结果连续性变化不明显。

2.2.2 搜索角

搜索角angel_1，angel_2，angel_3是指与搜索椭球体主方向匹配的旋转角。旋转椭球体由3次连续的旋转得到［17］。 首先围绕 z轴旋转，得到 angel_1（方位），然后再围绕x轴和 y轴分别旋转，得到 angel_2（倾角）和angel_3（倾向）。进行二维模拟时，必须仅仅指定一个旋转角。因为当angel_2非0时，二维样板就会“转出”二维空间，当投影到二维平面时，样板形状发生了改变，因此，进行二维模拟时，angel_2应始终为0。例如，在 xy空间进行二维模拟时，只需设定angel_1，而angel_2，angel_3应被设置为0，否则将得不到理想的模拟效果。

图4展示了旋转角设置不同值时的模拟效果。hx=hy=100，angel_1，angel_2 分别设置为 0°，45°，90°，组合形式共有9种。

图4 搜索角敏感性分析

当 angel_2=0°时（见图 4c，4f，4i），angel_1 值的不同对河道形态的再现没有影响，这是因为搜索邻域近似为圆形（hx=hy），在xy象限内的旋转是无效的。

当 angel_2=45°时（见图 4b，4e，4h），原始的圆形样板旋转出xy象限变成了一个椭球体样板。改变angel_1会导致伸长的椭球体在xy象限内的旋转。模拟结果只捕捉到一个方向上的结构信息，而丢失了另一个方向上的信息。 angel_1=0°或 90°（见图 4b，4h）与hx=10，hy=100 和 hx=100，hy=10（见图 3f，3h）得到的结果相似。

当 angel_2=90°时（见图 4a，4d，4g），搜索椭球体折合成了一条直线，将捕捉不到xy象限的信息。

2.3 旋转角与仿射率

在Snesim中，训练图像应该是平稳的，即训练图像内目标体的几何构型及目标形态在全区基本不变，不存在明显趋势或局部的明显变异性。如果直接使用非平稳训练图像，由于高频率出现的数据模式会控制模拟结果形态，特定位置上有序的相排列模式便无法再现［18］。鉴于大多数地质结构都是非平稳的，需要将训练图像中的平稳与非平稳信息融合起来。例如，在扇三角洲沉积体系中，河道由扇根延伸到扇缘呈发散状，且河道宽度向下游呈递减趋势。为表征这2个实际存在的现象，Zhang和Journel提出局部旋转角与仿射率这2个与位置有关的参数来约束建模，分别用于控制河道局部的流向与河道宽度［19］。

设置参数时，首先根据沉积体系特征手绘旋转角与仿射率图像（见图5a，5b），大小与训练图像一致，分区进行编号，分别转换为参数文件格式保存。然后，加载旋转角与仿射率的参数文件，并复制到新建网格下。采用分区思想，模拟区被划分为三部分，河道流向在各区域（0，1，2）的旋转角分别设置为 75°，45°，15°，河道宽度在各区（0，1，2）的仿射率分别乘以 1.2（北西），0.8（中部），0.5（南东）。二维图像的模拟中，z方向的仿射率均为1。

模拟结果显示：旋转角很好地控制住了河道的流动模式，且模拟出来的河道是连续的；仿射率对河道宽度也有影响，河道宽度向下游呈递减趋势（见图5c）。

2.4 多重网格层数

为了捕捉大规模的结构信息，在序贯模拟中要用到多重网格模拟。首先用大尺度样板在粗网格上模拟，之后再换较小尺度的样板在较细的网格上模拟，直到用原始样板在最细的网格上模拟。每层样板只改变大小而形状不变。这种机制确保了算法在满足原始采样数据的同时，能够捕捉到不同尺度的结构信息［16］。

多重网格层数（m）对模拟结果影响很大。如果设置为1，程序会直接模拟到最细的网格，而非逐渐模拟到最细网格，这样会导致只有在原始样板大小范围内的结构信息被捕捉到，得到的模拟结果是不合理的（见图6a）。当多重网格层数增加至2，3，4时，更大规模的结构信息便可以被捕捉再现（见图6b—6d）。

当网格层数继续增加时，模拟结果并未得到改进（见图6e，6f）。这是因为，当网格很粗时，相应的用来扫描训练图像的样板规模会大于训练图像的规模，导致大的数据事件很难被找到。此时数据事件就会相应缩小，而这就等同于使用较小的数据样板进行扫描。

图5 Snesim算法用于扇三角洲体系模拟

图6 多重网格层数敏感性分析

3 结论

1）目标边际分布的设置要与训练图像边际概率接近，当二者差别很大时，建议产生一个新的训练图像，使它的边际比例与目标相比例接近，而不建议使用更高的伺服系统参数去校正。

2）在Snesim中，数据样板由搜索椭球体参数决定，搜索半径控制样板的搜索范围，搜索角控制椭球体的方位，搜索角的设置要与模拟的维度相适应；在模拟二维河道沉积体系中，当hx=hy时，模拟结果较为理想，搜索半径和搜索角的设置应视训练图像特点而定。

3）训练图像应该是平稳的，局部旋转角与仿射率可以将相分布的非平稳信息融合起来。

4）多重网格模拟中，网格层数取决于最大尺度结构信息的大小。

［1］ 尹艳树，张昌民，李少华．多点地质统计学原理、方法及应用［M］．北京：地质出版社，2013：1-6.

［2］ 向传刚.运用多点地质统计学确定水下分流河道宽度及钻遇概率［J］.断块油气田，2015，22（2）：164-167.

［3］ 刘超，谢传礼，Yannick Tepinhi，等.多点地质统计学在储层相建模中的应用［J］.断块油气田，2015，22（6）：760-764.

［4］ 吴胜和，李文克.多点地质统计学：理论、应用与展望［J］．古地理学报，2005，7（1）：137-144.

［5］ 李少华，张昌民，尹艳树.河流相储层随机建模的几种方法［J］．西安石油学院学报（自然科学版），2003，18（5）：10-16.

［6］ 裘怿楠，贾爱林.储层地质模型 10 年［J］.石油学报，2000，21（4）：101-104.

［7］ 石书缘，尹艳树，冯文杰，等.多点地质统计学建模的发展趋势［J］.物探与化探，2012，36（4）：655-660.

［8］ STREBELLE S，JOURNEL A．Reservoir modeling using multiple-point statistics［R］．SPE 71324，2001．

［9］ STREBELLE S．Conditional simulation of complex geological-structures using multiple-point statistics［J］．Mathematical Geology，2002，34（1）：1-21．

［10］李少华，尹艳树，张昌民．储层随机建模系列技术［M］．北京：石油工业出版社，2007：55-68．

［11］尹艳树，张昌民，李玖勇，等.多点地质统计学研究进展与展望［J］．古地理学报，2011，13（2）：245-252.

［12］周金应，桂碧雯，林闻．多点地质统计学在滨海相储层建模中的应用［J］．西南石油大学学报（自然科学版），2010，32（6）：70-73．

［13］张伟，林承焰，董春梅．多点地质统计学在秘鲁D油田地质建模中的应用［J］．中国石油大学学报（自然科学版），2008，32（4）：24-27．

［14］骆杨，赵彦超．多点地质统计学在河流相储层建模中的应用［J］．地质科技情报，2008，27（3）：68-71．

［15］段冬平，侯加根，刘钰铭，等．多点地质统计学方法在三角洲前缘微相模拟中的应用［J］．中国石油大学学报（自然科学版），2012，36（2）：22-26．

［16］王家华，马晓鸽.多点地质统计学在储层建模中的应用［J］.石油工业计算机应用，2012，74（2）：15-16.

［17］ REMY N，BOUCHER A，WU J.Applied geostatistics with SGeMS：a user′sguide［M］.Cambridge：CambridgeUniversityPress，2009：26-29.

［18］ LIU Y.Using the Snesim program for multiple-point statistical simulation［J］.Computers&Geosciences，2006，32（10）：1544-1563.

［19］ Zhang T，Journel A.Merging prior structural interpretation and local data：the multiple-point geostatistics answer［C］//Stanford Center for Reservoir Forecasting Annual Report 16.Stanford：Stanford University，2002.

（编辑 赵卫红）

Parameter sensitivity analysis of multiple-point geostatistical Snesim program

WANG Hong,LI Shaohua
(College of Geosciences,Yangtze University,Wuhan 430100,China)

Snesim is a multiple-point geostatistical program which was applied to reservoir modeling for the first time.This paper makes the first attempt.Using sinuous channels as training image,this paper studies the sensitivities of important input parameters such as target proportion,servosystem parameter,search radii and angles for search ellipsoid,rotation angles and affinity,number of multiple grids.The analysis shows that:the target proportion should not be too different from that of the training image;the simulated channel proportion can approach the target proportion by using high servosystem parameters,whereas an excessive high servosystem parameter is not recommended as it may reduce the channel continuity;the search neighborhood should be adapted to the dimensions of the structures to be reproduced;the non-stationary information typically found for facies distribution can be incorporated into stationary information using rotation and affinity ratio parameters;multiple-grid simulation is always recommended,the number of grid levels depends on the size of the largest scale structures.These understandings can be used as references and guidance for reservoir modeling with Snesim.

multiple-point geostatistics;Snesim program;reservoir modeling;parameter sensitivity analysis

TE32+1

A

国家自然科学基金项目“一种薄夹层精细地质模型的粗化方法——网格边缘属性建模法”（41572121）；湖北省创新群体项目“储层精细表征与建模”（2016CFA024）

10.6056/dkyqt201704012

2016-12-09；改回日期：2017-04-26。

王红，女，1991年生，在读硕士研究生，研究方向为储层地质建模。 E-mail：603590432@qq.com。

王红，李少华.多点地质统计学算法Snesim参数敏感性分析［J］.断块油气田，2017，24（4）：490-494.

WANG Hong，LI Shaohua.Parameter sensitivity analysis of multiple-point geostatistical Snesim program［J］.Fault-Block Oil&Gas Field，2017，24（4）：490-494.