抗噪的多尺度形态学边缘检测算法
刘黎辉 张 剑 谭芳芳 李 巍
(湖南科技大学信息与电气工程学院,湘潭,411201)
抗噪的多尺度形态学边缘检测算法
刘黎辉 张 剑 谭芳芳 李 巍
(湖南科技大学信息与电气工程学院,湘潭,411201)
为了使图像边缘检测算法的抗噪声能力更强,能检测到更加丰富的边缘信息,在多尺度形态学边缘检测算法的基础上,提出一种抗噪的多尺度形态学边缘检测算法。一方面,用小波变换法替代常用的加权平均法来融合各尺度下获取的边缘图像,对小波分解后得到的低频系数和高频系数分别采取不同的融合策略,从而有效地保留边缘的细节信息,使得融合后获得的图像清晰且细节丰富。另一方面,在用不同尺度的结构元素检测图像边缘时都采用抗噪的检测算法,因此,该算法具有较强的抗噪声能力。仿真结果表明,该算法既能有效地降低噪声对检测结果的影响,又能获得较理想的边缘图像。
边缘检测;形态学;多尺度;抗噪声;小波融合
引 言
图像边缘是指其周围像素点的灰度值有明显不同的像素点的集合,它是图像的最基本特征之一,同时也是对图像进行分析和理解的基础。由于边缘通常存在于目标和背景之间或者区域与区域之间,因此,它是图像分割的重要依据。常用的Sobel,Canny等算子通过计算图像中局部小区域的差分来实现边缘检测,因此这类边缘检测算子对噪声比较敏感[1]。而形态学边缘检测器主要将数学形态学中的基本算子组合起来进行图像边缘检测,这种检测方式虽然对噪声依然敏感,但不会放大噪声。并且由于数学形态学边缘检测算法具有算法简单、运算速度快等优点,近年来成为了研究热点并在医学图像处理、缺陷检测和声呐图像处理等领域得到了广泛的应用[2-5]。形态学边缘检测算法的检测效果很大程度上依赖于结构元素的选取。若只采用单一尺度和形状的结构元素进行边缘检测,由于受到结构元素的限制,检测出来的边缘图像会丢失某些方向上的信息,从而使检测出的边缘信息不够丰富,难以达到预期的检测效果。为了获取更加全面的边缘信息,学者们逐渐提出了多种基于多尺度多结构元素的形态学边缘检测算法。此类方法的基本思想是采用不同尺度、不同形状的结构元素对图像进行边缘检测,然后将多个检测结果进行融合,得到最终的边缘图像[6-8]。融合通常采用加权平均法,根据图像熵比值、峰值信噪比(Peak signal to noise ratio,PSNR)或经验值选取权值。此外,由于实际应用场合的图像大多含有噪声,这会使得边缘检测结果不准确,直接影响后续的图像分析效果,因此提高算法的抗噪声能力也非常重要,基于这个需求,有学者针对噪声的特点构造出具有抗噪声能力的边缘检测算子,并提出了抗噪声的边缘检测算法[8-10]。
本文在多尺度形态学边缘检测方法的基础上,用每一种尺度的结构元素检测图像边缘时都采用抗噪的检测算法,以便获得较好的抗噪能力。检测到不同尺度的边缘信息后,常见的融合方法为加权平均法,但这种方法融合后的图片整体灰度较暗,边缘线条不明显。本文采用小波变换的方法进行融合,且对小波分解后的高频信号和低频信号分别采用不同的融合策略,尽可能多地将各尺度下的边缘信息融合到最终边缘图片中,使得融合后的边缘图像更加清晰,包含更多边缘信息。
1 形态学边缘检测原理1.1 基本的形态学算子
数学形态学的基本运算是膨胀、腐蚀、开启和闭合。对于灰度图像,选取一幅输入图像f(x,y)和1个结构元素g(x,y),设f(x,y)和g(x,y)的定义域分别为Dy和Dg,则这4种基本运算定义如下[11]:
定义1 用结构元素g对图像f进行灰度膨胀,记为f⊕g,其定义为
f⊕g(x,y)=max{f(x-s,y-t)+g(s,t)|(x-s,y-t)∈Df,(s,t)∈Dg}
(1)
定义2 用结构元素g对图像f进行灰度腐蚀,记为fΘg,其定义为
fΘg(x,y)=min{f(x-s,y-t)-g(s,t)|(x-s,y-t)∈Df,(s,t)∈Dg}
(2)
定义3 灰度开启运算记为f∘g,它是指用结构元素g对图像f先腐蚀,再膨胀,即
f∘g=(fΘg)⊕g
(3)
定义4 灰度闭合运算记为f·g,它是指用结构元素g对图像f先膨胀,再腐蚀,即
f·g=(f⊕g)Θg
(4)
灰度膨胀会使图像变得更明亮,而且能够减弱或去除图像中尺寸小且暗的细节部分。灰度腐蚀与灰度膨胀的作用相反,会使图像变得更暗,且会减弱图像中尺寸小且明亮的细节部分。灰度开启和闭合则能够在基本保持图像整体灰度不变的情况下分别去除图像中小于结构元素的明亮细节和暗细节[12]。
1.2 形态学边缘检测方法
数学形态学边缘检测是指将形态学的基本运算组合起来构成形态学边缘检测算子,然后用其来检测图像中的边缘信息。式(5~7)给出了几种基本的形态学边缘检测算子的形式,式(5)为膨胀型边缘检测算子,这种方法提取图像的外边缘。式(6)为腐蚀型边缘检测算子,这种方法提取图像的内边缘。式(7)为膨胀腐蚀型边缘检测算子,也被称为形态学梯度边缘检测算子,这种方法可以检测出图像中高亮部分的外围边缘,是比较常用的一种形态学边缘检测算子。以这几种基本算子为基础,将形态学基本运算进行不同的组合,可以衍生出多种多样的形态学边缘检测算子,如
E(x,y)=f(x,y)⊕g(x,y)-f(x,y)
(5)
E(x,y)=f(x,y)-f(x,y)Θg(x,y)
(6)
E(x,y)=f(x,y)⊕g(x,y)-f(x,y)Θg(x,y)
(7)
2 改进的多尺度形态学边缘检测算法
形态学边缘检测算法的性能很大程度上依赖于结构元素的选取,选取不同的结构元素,将得到不同的检测结果。结构元素主要有形状和尺度两个基本属性,结构元素形状影响检测到的边缘方向,通常需要根据实际需要选取合适的结构元素。结构元素的尺度影响检测到的边缘尺度,同时还影响检测算法的去噪声能力。采用小尺度的结构元素进行边缘检测时能较好地检测到边缘细节,但去噪声能力不强。采用大尺度的结构元素进行边缘检测时的去噪声能力明显变强,但检测到的边缘比较粗,边缘的细节信息被模糊化了[13]。因此,在用形态学进行边缘检测时,若只采用单一形状和尺度的结构元素,得到的检测结果通常具有很大的局限性。为了结合大尺度和小尺度结构元素各自的优点,利用大尺度结构元素的抗噪声能力来抑制噪声,利用小尺度结构元素更好地定位边缘位置并提取边缘的细节信息。可以用不同尺度的结构元素对图像进行形态学梯度边缘检测,得到多张边缘图像,然后再将这些图像融合成最终的边缘图像。文献[3]中给出了一种多尺度形态学梯度算子,假设gi(0≤i≤n)为一组大小不同的结构元素,各结构元素大小为(2i+1)×( 2i+1),则可使用式(8)获取边缘图像,则
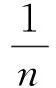
(8)


(9)
式中:w(q)为权值;离p点越近,权值越大。图像A和B的低频系数矩阵的区域方差显著性表示为G(A,p)和G(B,p)。此外,用M2(p)定义图像A和B的低频系数矩阵在p点的区域方差匹配度,则
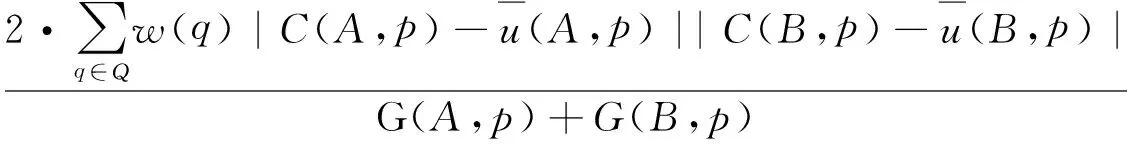
(10)
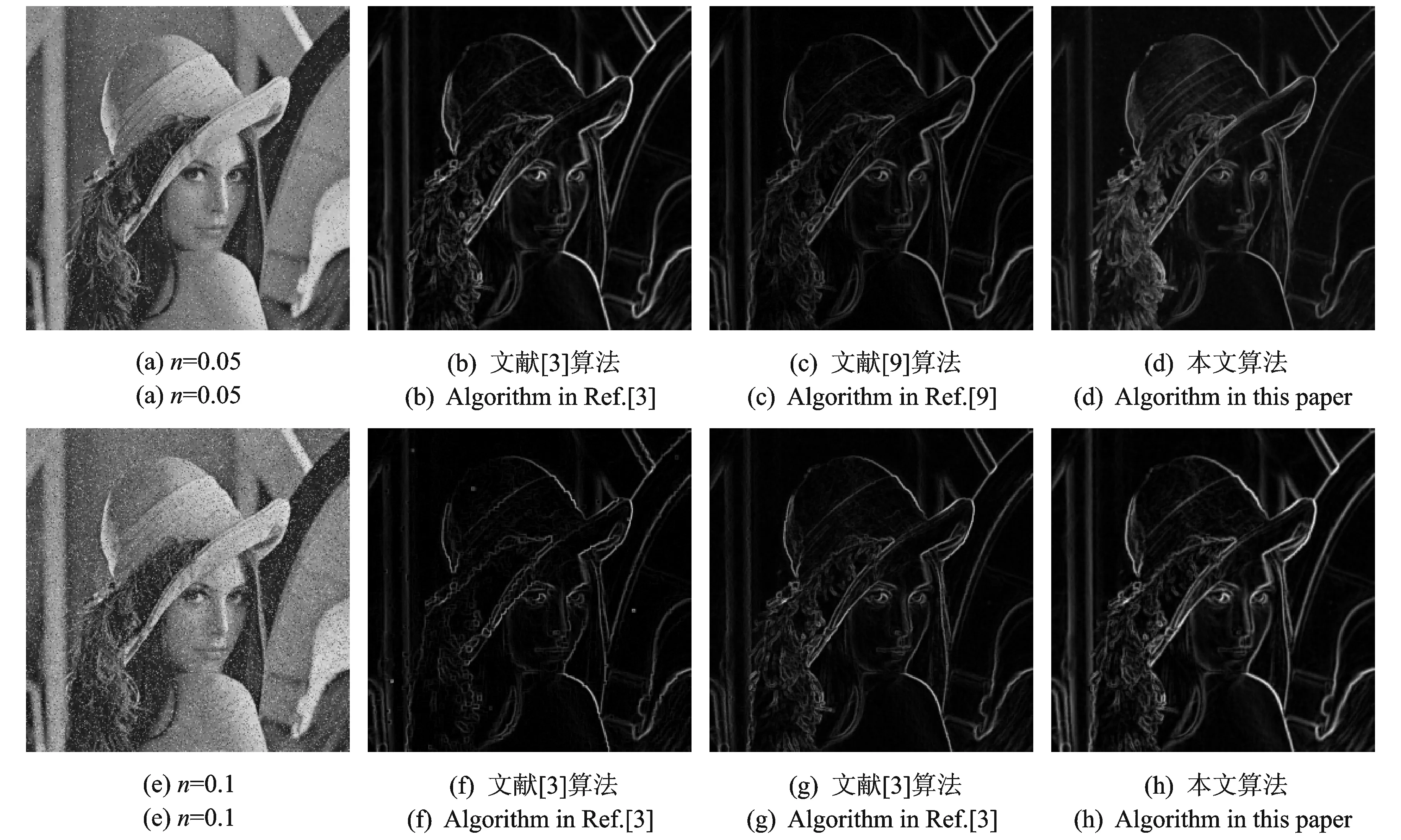
式中:M2(p)的取值在0~1变化,其取值越小,说明两幅图像低频系数矩阵的相关度越低。设T2为匹配度阈值,一般取0.5~1。当M2(p) (11) 当M2(p)≥T2时,采用平均融合策略,则 (12) 实际应用中的图像大多会被噪声污染,这些噪声会影响图像边缘检测的准确性,使得检测出的边缘图像包含许多伪边缘信息。因此为了提高图像边缘检测的准确性,图像边缘检测算法一定要具有一定的抗噪声能力。由于噪声同边缘信息一样都是高频信号,因此在滤除噪声的同时,很容易将图像的边缘信息也一同去除掉[15-16]。因此抗噪声的边缘检测算法要在有效地去除噪声和保留完整的图像边缘这两个目标之间找到一个折衷的方案,既有效地去除噪声,又能极大地保留图像边缘信息。文献[9]中提出了一种改进的抗噪形态学边缘检测算法 yd=(((f∘B1)·B2)⊕B2)∘B2-(f∘B1)·B2 (13) ye=(f∘B1)·B2-(((f∘B1)·B2)ΘB2)·B2 (14) Emin=min{yd,ye} (15) yde=yd+ye (16) y=yde+Emin (17) 式中:B1,B2分别为3×3的菱形结构元素和正方形结构元素。这种方法虽然能较好地去除图像中的椒盐噪声并检测到较完整的边缘信息,但这种方法所使用的结构元素只有一个尺度,同样会对图像的粗边缘和细节边缘不能兼顾,因此需要对这种方法进行改进,以便得到更好的检测效果。选取多个尺度的结构元素对图像进行边缘检测可以兼顾粗边缘和细边缘的提取,同时还能提高抗噪声能力。因此可以将文献[9]提出的抗噪形态学边缘检测算法与改进的多尺度形态学边缘检测算法相结合,构成一种抗噪的多尺度形态学边缘检测算法,这样便可获得更好的检测效果。抗噪的多尺度形态学边缘检测算法的实现步骤如下。 步骤1:选取n个不同尺度的结构元素组(由1个十字形结构元素和1个矩形结构元素组成),根据式(17)所示的抗噪形态学边缘检测算法得到n幅边缘图像。 步骤2:将这n幅边缘图像进行小波分解,对低频系数采用式(11)或式(12)给出的融合策略进行融合,对高频系数采用像素点绝对值取大原则进行融合。 步骤3:将融合后的系数进行小波逆变换,得到最终的边缘图像。 由于在用不同尺度的结构元素检测图像边缘时都采用了抗噪的检测算法,因此这种边缘检测算法具有较好的抗噪声能力。引入多尺度方法能检测出比较完整的边缘信息,而且对图像融合方式进行了改进,使得检测出的边缘线条也很清晰。 图1,2分别采用文献[3]中的加权平均法和本文提出的小波变换法进行仿真来比较两种融合算法的融合效果。从主观上看,采用加权平均法融合的图像比融合前的图像整体偏暗,特别是荷花的花瓣边缘部分,而采用小波变换融合的图像整体亮度比较好。另外小波变换法比加权平均法融合得到的边缘信息更加丰富,特别是细小的边缘信息,并且边缘线条的清晰度更高,这一点在″Lena″图像中很容易看出。 图1 荷花图像加权平均法与小波变换法融合效果对比Fig.1 Fusion effect comparison between weighted mean and wavelet transform method in Lotus image 图2 Lena图像加权平均法与小波变换法融合效果对比Fig.2 Fusion effect comparison between weighted mean and wavelet transform method in Lena image 为了更加客观地对图像融合质量进行评价,本文选取信息熵、平均梯度和灰度均值这3项指标来对两种融合方法进行评价。信息熵是衡量图像信息丰富程度的一个重要指标,图像的熵值越大,表明图像包含的信息量越大,其融合质量越好。平均梯度是衡量图像清晰程度的指标,它反映了图像中某一方向上的灰度变化率,平均梯度较大说明图像清晰度高。因此可以用平均梯度衡量图像中的微小细节反差,灰度均值反映整幅图像的平均亮度。通常情况下,其值越大越好。表1是两种融合方法的融合效果评价表,从表1中可以明显看出,小波变换法的融合效果较好一些。 表1 融合效果评价 为了进一步分析本文提出的抗噪多尺度形态学边缘检测算法的性能,分析本文算法的抗噪声能力,选用带噪声的″Camera Man″图像和″Lena″图像进行仿真,并用文献[3]提出的多尺度多结构元素形态学边缘检测算法、文献[9]提出的抗噪形态学边缘检测算法与本文算法进行对比,仿真时只采用3像素×3像素和5像素×5像素两个尺度的结构元素。每种图像分别含有噪声密度为0.05和0.1的椒盐噪声,图3,4分别是各种算法对含噪声图片的边缘检测结果。从图3,4中可以看出,在噪声浓度较低时,各算法检测出的边缘图像都较好,但相比而言,文献[9]算法由于采用单一尺度的结构元素,检测出的边缘信息不是很丰富。在添加噪声后,文献[3]算法效果最差,可以看出有一部分噪声并没有去除。文献[9]算法检测的结果与未添加噪声时差别不大,说明其算法抗噪声能力较强。本文给出的算法抗噪声能力也不错,并且检测到的边缘信息依然比较丰富。为了更加客观地评价这几种算法的性能,对图3,4所示的边缘图像采用均方差(Mean square error, MSE)和PSNR这两项指标来评价,以便比较各算法的抗噪声能力,评价详情见表2。从表2可以看出,本文算法和文献[9]算法的抗噪声能力都不错,但本文算法的效果更好一点。 图3 各种算法对″Camera Man″图像边缘检测结果Fig.3 Edge detection results of ″Camera Man″ image by using various algorithms 图4 各种算法对″Lena″图像边缘检测结果Fig.4 Edge detection results of ″Lena″ image by using various algorithms 图像MSEPSNR文献[3]算法文献[9]算法本文算法文献[3]算法文献[9]算法本文算法″CameraMan″(0.05)11.506410.86978.754137.794936.001340.0531″CameraMan″(0.1)12.100511.05139.057531.794935.954738.8956″Lena″(0.05)13.102614.95477.562136.794936.848139.3103″Lena″(0.1)13.601715.07557.621731.060134.187337.2417 本文在多尺度形态学边缘检测算法的基础上提出了一种抗噪的多尺度形态学边缘检测算法。在多尺度形态学边缘检测中通常采用加权平均法来对多张边缘图像进行融合。这种方法虽然简单,但是由于对整张图片都采用相同的融合策略,效果不佳。本文对图像融合部分进行了改进,采用基于小波变换的方法对多幅边缘图像进行融合,并且对小波分解后的低频和高频系数分别采用不同的融合策略以便获得更好的融合效果。在抗噪声方面,本文算法在每一尺度下都构造了抗噪的边缘检测算子来进行边缘检测,从而提高抗噪声能力。仿真结果表明,采用本文提出的小波融合方法来对边缘图像进行融合,融合后的边缘图像包含更丰富的边缘信息且线条清晰。当图像被噪声污染时,本文算法依然能够有效地抑制噪声对检测结果的影响,检测出较为准确的边缘图像,因而能够适用于更多的应用场合。 [1] Caixia D,Guibin W,Xinrui Y. Image edge detection algorithm based on improved canny operator[C]∥Proceedings of the 2013 International Conference on Wavelet Analysis and Pattern Recognition. Rhode Island:IEEE Computer Society Press,2013:168-172. [2] Wang Xiufang,Zhang Xingyuan,Gao Running. Research of image edge detection based on mathematical morphology[J].International Journal of Signal Processing,Image Processing and Pattern Recognition,2013,16(5):227-236. [3] 张利红,梁英波,吴定允,等. 基于改进多尺度形态学的带钢缺陷图像边缘检测[J].激光与红外,2014,44(3):330-334. Zhang Lihong,Liang Yingbo,Wu Dingyun,et al. Strip steel surface defects imaging edge inspection based on improved multi-scale morphology[J].Laser & Infrared,2014,44(3):330-334. [4] 景少玲,白静,叶鸿瑾. 改进的形态学肺部图像边缘检测[J].数据采集与处理,2014,29(1):134-141. Jing Shaoling,Bai Jing,Ye Hongjin. Edge detection of lung images based on improved morphology[J]. Journal of Data Acquisition and Processing, 2014,29(1):134-141. [5] 郭海涛,徐雷,赵红叶,等. 一种抑制声呐图像散斑噪声的形态学滤波器[J].仪器仪表学报,2015,36(3):654-660. Guo Haitao,Xu Lei,Zhao Hongye,et al. A morphological filter for despeckling of a sonar image[J].Chinese Journal of Scientific Instrument,2015,36(3):654-660. [6] 孟婷婷,余谅,李寿敏,等. 一种基于改进的形态学算子的边缘检测算法[J].计算机工程与科学,2011,33(8):112-116. Meng Tingting,Yu Liang,Li Shoumin,et al. An edge detection algorithm based on improved morphologic operators[J].ComPuter Engineering & Science,2011,33(8):112-116. [7] 张文娟,康家银. 基于多尺度分析和数学形态学融合的边缘检测[J].计算机应用与软件,2011,28(9):85-88. Zhang Wenjuan,Kang Jiayin. Edge detection based on fusion of multi-scale analysis and mathematical morphology[J].Computer Applications and Software,2011,28(9):85-88. [8] Wang Huifeng,Zhang Guili,Li Xiaoming. Research and application of edge detection operator based on mathematical morphology[J].Computer Engineering and Applications,2009,31:223-226. [9] 邓彩霞,王贵彬,杨鑫蕊. 改进的抗噪形态学边缘检测算法[J].数据采集与处理,2013,28(6):739-745. Deng Caixia,Wang Guibin,Yang Xinrui. Improved algorithm of morphology in edge detection for noise resistance[J].Journal of Data Acquisition and Processing,2013,28(6):739-745. [10]于博,牛铮,王力,等. 抗噪形态学边缘检测新算子图像边缘检测[J].信息技术,2012,36(3):10-12. Yu Bo,Niu Zheng,Wang Li,et al. A new algorithm of morphology in edge detection to resist the noise[J].Information Technology,2012,36(3):10-12. [11]王贵彬. 基于Canny算子与形态学融合的边缘检测算法[D].哈尔滨:哈尔滨理工大学,2014. Wang Guibin. Fusion edge detection method based on canny operator and morphology[D].Harbin:Harbin University of Science and Technology,2014. [12]Rafael C G,Richard E W. Digital image processing[M].Third Edition. Beijing:Publishing House of Electronics Industry,2010:687-690. [13]亢洁,杨刚. 自适应权重形态学边缘检测算法仿真研究[J].计算机工程与应用,2010,46(17):163-167. Kang Jie,Yang Gang. Simulation research of adaptive weight morphological edge detection algorithm[J].Computer Engineering and Applications,2010,46(17):163-167. [14]赵小川. 现代数字图像处理技术提高及应用案例详解(Matlab版)[M].北京:北京航空航天大学出版社,2012. Zhao Xiaochuan. Modern digital image processing technology and application case explanation (Matlab Edtion)[M].Beijing:Beihang University Press,2012. [15]Sergey T,Becerikli Y. An improved image de-nosing method using a wavelet based neural network filter[C]∥18th International Conference on Systems,Signals and Image Processing. Rhode Island:IEEE Computer Society Press,2011:123-126. [16]赵晓丽, 吴飞. 基于各向异性高通滤波的图像边缘检测算法[J]. 计算机工程与科学, 2013, 35(7):137-142. Zhao Xiaoli, Wu Fei. Edge detection algorithm based on anisotropic high-pass filtering[J]. Computer Engineering & Science, 2013,35(7):137-142. To reinforce the noise resistance capability of image edge detection algorithm better and refine edge information detection, a multi-scale morphology algorithm for image edge detection with noise resistance is proposed. Moreover, wavelet transform method is utilized to replace the commonly used weighted mean method and the edge images are obtained by each scale fused. The low frequency and high frequency coefficients of the wavelet decomposition are adopted respectively by different fusion strategies. Thus the edge details are effectively preserved. The fused image is clear and has rich details. Anti-noise detection algorithm is used to detect the edge of image using different scales of structuring elements. Hence, the algorithm becomes robust to the noise. The simulation result shows that the proposed algorithm can effectively reduce the influence of noise on detection results obtaining the ideal edge image. edge detection; morphology; multi-scale; noise resistance; wavelet fusion 国家自然科学基金面上(51374107,51275169)资助项目;湖南省教育厅重点科研(15A066)资助项目;湖南省研究生科研创新(CX2015B486)资助项目。 2015-10-30; 2016-10-09 TP391.41 A 刘黎辉(1991-),男,硕士研究生,研究方向:数字图像处理,E-mail:llh-liulihui@163.com。 李巍(1990-),男,硕士研究生,研究方向:数字图像处理。 张剑(1974-),男,博士,教授,研究方向:数字图像处理。 谭芳芳(1990-),女,硕士研究生,研究方向:数字图像处理。 Multi-scale Morphology Algorithm for Image Edge Detection with Noise Resistance Liu Lihui, Zhang Jian, Tan Fangfang, Li Wei (School of Information and Electrical Engineering, Hunan University of Science and Technology, Xiangtan, 411201, China)
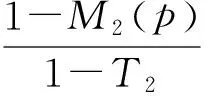
3 抗噪的多尺度形态学边缘检测算法
4 仿真与分析




5 结束语





