基于贝叶斯分位数回归模型的余额宝收益风险分析

陈耀辉白兰

(南京财经大学 经济学院， 江苏 南京 210023)

基于贝叶斯分位数回归模型的余额宝收益风险分析

陈耀辉白兰

(南京财经大学 经济学院， 江苏 南京 210023)

主要对余额宝收益风险进行了分析。首先采用定性分析的方法，确定余额宝收益率的影响因素。然后比较分位数回归和最小二乘估计的区别，再利用贝叶斯分位数回归模型优化分位数回归结果，探究余额宝7日年化收益率、上海同业拆借率、国债收益率、银行理财产品收益率、货币供应量之间的关系。比较前后模型的拟合结果，发现贝叶斯分位数回归更适合表达余额宝收益率及其影响因素的关系，通过多次迭代，各解释变量在余额宝收益率各分位数上对其影响趋势更加明显。利用贝叶斯分位数回归的结果，可知余额宝收益率变动带来的风险分别为流动性风险、投资风险、市场风险，同时余额宝还面临着同类竞争。余额宝可以通过增强自身的资金管理方式、优化资产组合比率、优化资资产组合项目来适当降低风险。

分位数回归；余额宝7日年化收益率；贝叶斯分位数；余额宝风险

余额宝2013年5月正式发行，自发行以来发展迅速，被关注度只增不减。作为金融产品与互联网技术结合的一次尝试，余额宝取得了巨大成功，开辟了一个全新的互联网金融市场，带动了我国利率市场化进程。在余额宝之后，越来越多类似产品推出，这些产品的存在逐渐改变了人们的生活习惯，如从支付方式到理财观点等等。同时，余额宝的存在也给传统金融行业带来冲击。通过对余额宝收益率影响因素的分析，能够更加清晰地分析余额宝的风险，给余额宝客户提供实践价值。国内许多学者都对余额宝进行了研究，从研究方法上可以大致将该类文章分成定性研究和定量研究2类。

定性研究系统地描述了互联网金融的运作方式以及以互联网为交易平台对金融行业的利弊，重点强调了这种运作模式带来的风险，详细描绘了风险的种类和原因：王天宇详细介绍了余额宝的运作模式，以及分析了余额宝可能对我国传统金融行业造成的影响[1]；郑椒瑾阐述了互联网金融行业发展对商业银行的影响，主要以余额宝为例，通过互联网金融行业的发展会在一定程度上降低商业银行的理财产品的销售，削弱商业银行的基金代销功能，降低商业银行的市场地位，并且提出了相应解决措施[2]；刘晖等首先分析了余额宝的运作模式和发展历程，同时指出余额宝的发展也会遭遇障碍，余额宝缺乏信用优势，难吸引大额资金，其资金规模的大小会给其流动性带来管理压力[3]；陈川通过对余额宝投资对象的分析，剖析了其低风险的原因。并且将余额宝较高收益率归结于银行对存款的需求，同时认为短期资金利率非市场化也会使余额宝收益率增加[4]；认为余额宝类似于“团购发起人”的运作模式，具有极大创新性刘东[5]；李克穆从3个方面对互联网金融的风险进行总结，认为余额宝的风险分别为技术类风险、业务类风险、法律类风险[6]。

定量分析的切入点较小，针对风险的不同方面可以利用不同的定量方法对风险的大小进行刻画，再进一步对风险进行分析：曾建光从用户对网络安全的关注度出发，利用百度大数据，发现对于网络安全风险感知的研究也促进了对余额宝风险、资产定价以及市场行为的观察，同时通过回归结果可以看出移动互联网端较PC端投资者对风险补偿的要求更多[7]；周怡君基于层次分析法构建了余额宝风险评价的量化指标体系，同时将量化指标按照等级排序为流动风险、法律风险、市场风险、操作风险、技术风险[8]；刘冬青对余额宝的收益和费用情况做了详细描述，建立线性回归模型，定量分析余额宝的收益率与上海银行间同业拆借率的关系，研究发现两者之间没有长期相关性，认为余额宝的高收益率可能来自于余额宝前期自身补贴[9]；蒋玥的研究与刘冬青的研究结论相差甚远，实证分析了影响余额宝收益率的因素，认为余额宝收益率与商业银行协议存款利率之间存在明显的线性关系，得出余额宝的收益率受到商业银行协议存款的上一期以及其自身利率的上一期的影响[10]；陆敬筠等定量研究了余额宝收益率与上海银行间同业拆借率的变化趋势，分别用二周期、一月期、三月期的银行间拆借率建立多元线性关系。研究表明，银行间拆借率对余额宝的收益率的影响是显著的，但是不同期的拆借率对余额宝的影响不同，其中一月、三月带来的影响是正向的，二周期的同业拆借率的影响是负向的[11]；何建敏等利用集成经验模态分解方法，对原有的信号做平稳化处理，并将信号逐级分解为具有不同特征尺度本征模函数的多分辨率信号予以分析方法，发现其能够准确地反映原始序列的内在波动特性；他们先利用集成经验模态分解法，将余额宝收益率分解为高频、低频、趋势分量，再建立VAR模型，通过对模型建立脉冲响应函数和利用方差分解分析，最终得到余额宝收益率影响因素分别为银行间同业拆借利率、银行存贷比、广义货币供应量、汇率[12]。

一、 余额宝的高收益性

余额宝的收益率较普通货币基金要高，远远超过银行同期活期存款。余额宝的出现对我国银行业造成了一定程度的冲击。余额宝的收益率从开始发行到现在先增加再减少近期又开始反弹，见图1，其中7日年化收益率最大达到6.763%，最少只有2.093%。

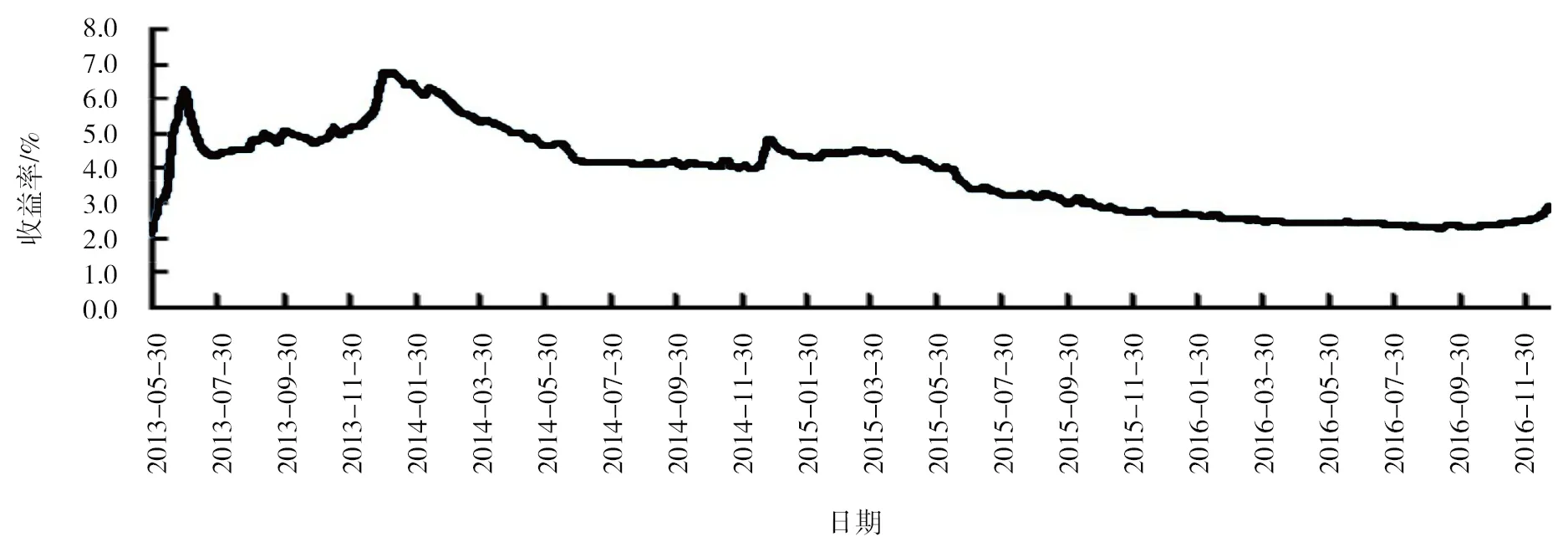
图1 2013年至2016年余额宝收益率的变化趋势

对余额宝收益率进行分析，可以从余额宝的资金流向开始，继而通过其资产组合的状况，分析影响余额宝收益率的因素。通过余额宝货币市场基金报告可以分析出余额宝的资产组合状况。从最近一期(2016年第四季度报告)报告中，可以得到报告期末余额宝的资金流向为固定收益投资、买入返售金融资产、银行存款和结算备付金合计以及其他资产，相关数据见表1。

同时利用报告的期末资金资产组合计算资产组合比重，其中70.27%为银行存款和结算备付金合计，17.95%为买入返售金融资产，11.58%为固定收益投资，0.2%为其他资产。所以余额宝收益影响程度最大的为银行存款和结算备付金，这部分资金的流向是银行间的协议存款，而银行间同业拆借率与这个部分资金的收益息息相关，所以要研究余额宝收益率的变动，可能就需要研究余额宝的收益率与银行间同业拆借率的关系。分析余额宝的利润见表2，从表2可以看出余额宝的收益99%都是来自于银行间的协议存款。也就进一步确定了余额宝收益率与银行间同业拆借率息息相关。

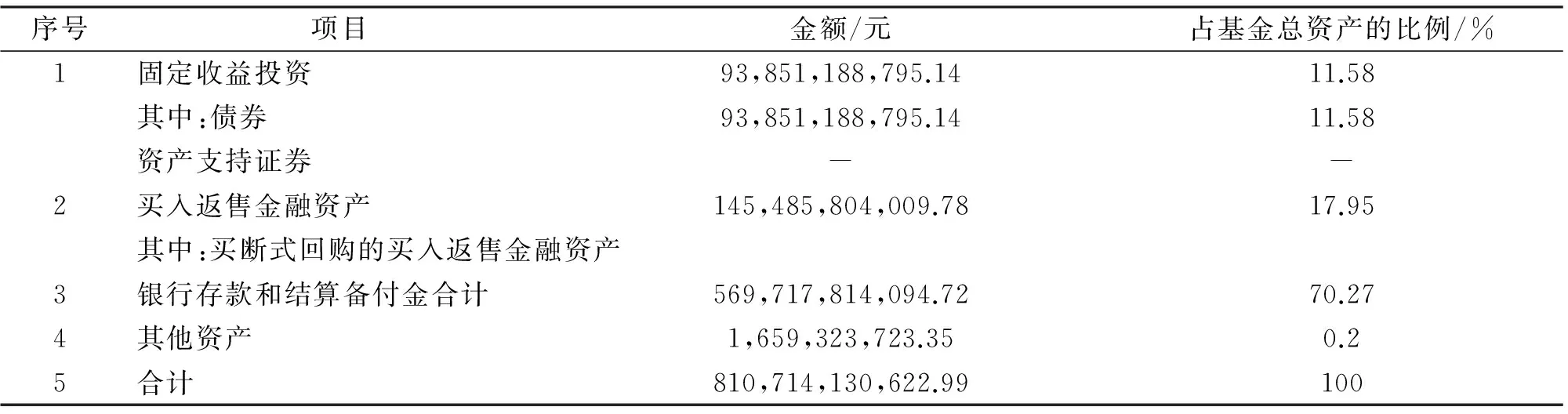
表1 2016年第4季度期末资金资产组合情况

表2 余额宝的利润表

笔者选取银行同业拆借率为解释变量，以余额宝7日年化收益率为被解释变量建立模型。之前对余额宝收益率的研究大都基于最小二乘法，但由于余额宝收益率的阶段趋势，所以拟采用分位数回归[3]，比较分析各分位点上系数的大小变化，实证分析随着余额宝的分位点的增加银行间同业拆借率的系数的变化规律， 余额宝的高收益是由其与银行的协议存款带来的，还是因为在其他项目上的投资带来的，即分析是否，如果两者同向增加则说明余额宝的高收益是由其与银行的协议存款带来的，如果两者具有相反方向，则说明银行间协议存款只给余额宝带来基本收益，而其高出一般收益的部分则是由其资产组合中其他方向的投资得来的。

二、 模型的构建

(一) 分位数回归模型

最常用的传统线性回归方法是普通最小二乘法，用最小二乘法估计的参数值很容易受到奇异点的影响，分位数回归是考察不同分位数水平下变量系数的变化情况[13]。分位数回归的结果只与样本数据本身有关，他们的取值不会受到其样本的密度分布或者样本中异常值的影响，因此在实际应用中，采用分位数回归处理样本数据无需满足样本的正态分布或近似正态分布假定，同时处理无法去除异常值样本的问题。

分位数基本定义如下:考虑随机变量X可以用一个(右连续)分布函数描述:

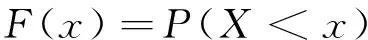
(1)

对于任意的0<τ<1,X的第τ分位数表示为F-1(τ)=inf{x:F(x)≥τ}，刻画了随机变量X的性质，表示占有比例为τ的样本数据在第τ分位数F-1(τ)之下，比例为1-τ样本数据在第τ分位数F-1(τ)之上。

简单的线性模型为：

(2)

其中，yi表示响应变量，xi表示自变量的向量，i=1,…,n，εi表示期望为0的随机误差，(β0，β)是未知参数变量。

分位数回归的估计可以通过式3完成最小值线性规划得以实现：

(3)

式(3)可以转化为：

(4)

定义损失函数ρτ(u)=u(τ-1(u<0))，从而可以将上述问题的解转化为：

(5)

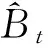
经济数据多有尖峰厚尾、结构突变等分布特征，不服从正态分布，所以利用最小二乘法进行分析不如分位数回归的效果好。

(二)基本模型改进——贝叶斯分位数回归模型

贝叶斯分位数回归是将贝叶斯估计方法与分位数回归结合起来，从而构建贝叶斯分位数回归模型，该方法的关键在于需要假设随机误差项是服从非对称的拉普拉斯分布(ALD)，拉普拉斯(LD)分布的密度函数为：

(6)

其中,-∞0，均值为μ，方差为2δ2。该布称为一型Laplace分布，正态分布被称为二型Laplace分布，最常用的最小二乘回归建立在二型Laplace分布的基础之上，但一型Laplace分布具有尖峰后尾的特征，更适合对金融时间序列数据进行拟合。

基于拉普拉斯分布，对原本对称的分布函数进行改进，转化为非对称的拉普拉斯分布(ALD)，如果随机变量X服从非对称拉普拉斯分布，其密度函数可以写为：

(7)

其中，0<τ<1为偏度参数，σ>0为尺度参数，-∞<μ<+∞为位置参数。对应的分位数函数为：

(8)

任意一个非对称的拉普拉斯分布都可以从一个对称的拉普拉斯分布得到。可以将标准化的密度函数写为：

(9)

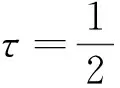
贝叶斯分位数回归是假设分位数模型的误差项为非堆成的拉普拉斯分布，μt～ALD(0,δ,τ),所以被解释变量的分布应该为yt～ALD(Qτ(yt|xt;β),σ,τ)其中偏度参数为0<τ<1，尺度参数为σ。可以得出回归模型的密度函数：

(10)

将损失函数带入回归模型的密度函数中则回归模型的密度函数可以写成：

(11)

再写出其似然函数：

(12)

在特定的τ分位数下，似然函数的极大值与分位数的极小值是等价的，所以可以通过求解似然函数的最值来得到分位数参数的估计值。同时利用蒙特卡洛抽样可以的到分位数回归参数的分布，同时对抽样的结果进行检验，观察回归参数是否收敛。

之前对余额宝收益率的研究大都基于最小二乘法，但由于余额宝收益率具有阶段趋势，所以笔者拟采用分位数回归，比较分析各分位点上系数的大小变化，同时通过贝叶斯理论让参数值更加精准，实证分析余额宝的高收益是由其与银行的协议存款带来，还是因为在其他项目上的投资，即分析随着余额宝收益率的分位点的增加影响因素的的变化规律。

三、 实证分析

(一) 数据选取

从wind数据库选取从余额宝成立日(2013年5月30日)到2016年12月底的7日年化收益率作为被解释变量(yeb)，同时选择相应时间的上海银行间同业拆借率(shibor)以日为计算周期、一年期国债收益率以日为计算周期(gb)、一年期银行理财产品收益率以周为计息周期(fb)、货币供应量(M2)以月为计算周期。考虑到周末以及节假日等因素，部分数据存在缺失的状况可能无法匹配，所以以日为计算周期的基础上，首先剔除不匹配的数据，再将以周为计算周期的银行理财产品收益率与相应日期匹配，最后将月货币供应量以每月30天平均，每月各日的货币供应量的值保持不变。

(二) 余额宝收益率分析

通过对余额宝收益率的时间序列图(图1)粗略判断收益率的变动情况，从总体上看余额宝的万份收益具有长期负效应，初步判断数据不平稳而且可能存在杠杆效应。同时按时间来观察数据，数据在一定时段中波动较大，而在另一时段中波动较小，表现出“波动集群”的特征。

在确定余额宝7日年化收益率拟合模型时，首先判断该数据是否具有正态性。

对数据进行Jarque-Bera检验，得到 Jarque-Bera统计量为29450.79，该统计量的p值近似为0，说明观测样本不服从正态分布。通过直方图可以看出观测样本的偏度为1.077475>0，说明余额宝7日年化收益率差分的时间序列是右偏的，从图形中可以看出其尾部的分布较正态分布要高，其峰度为27.01295>3，说明余额宝7日年化收益率差分的时间序列要高于正态分布，呈现出尖峰的特征。与金融性时间序列数据的高峰厚尾相符合。

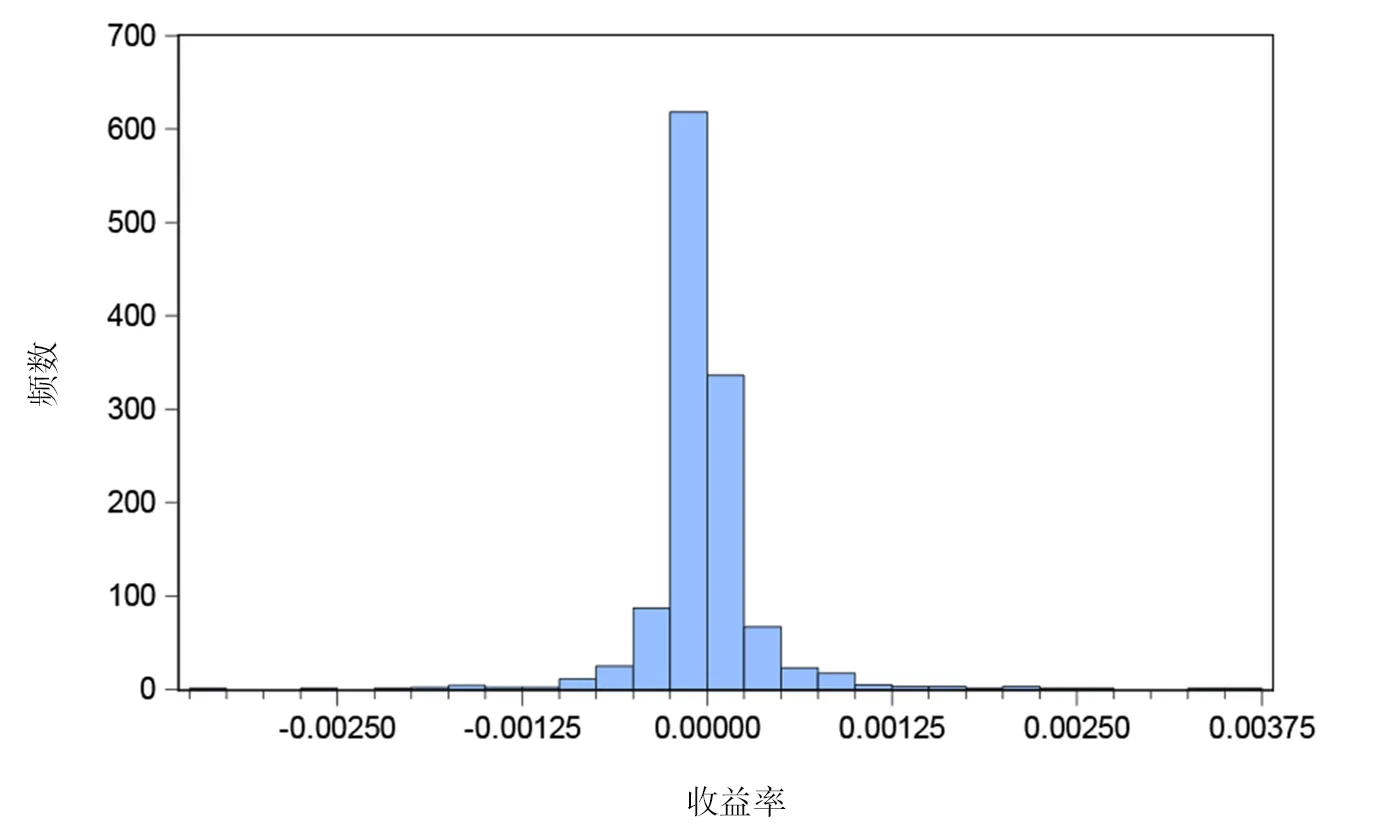
图2 余额宝7日年化收益率的直方图

对余额宝7日年化收益率进行初步探索， 发现该数据不服从正态分布，针对像余额宝这种具有尖峰后尾性质的金融时间序列数据，OLS(普通最小二乘法)、GARCH(广义自回归条件异方差模型)等传统条件均值模型对数据平稳性和误差项分布又有限定，所以这些条件均值模型不能全面准确反映两者作用规律。

(三)基于分位数回归模型的建立

为了探究余额宝收益率与其影响因素货币供应量、银行间同业拆借率、银行理财产品收益率、国债收益率之间的关系，选择4个分位数点，分别是τ=0.2、0.4、0.6、0.8。先做分位数回归，比较分位数回归与最小二乘回归的区别。

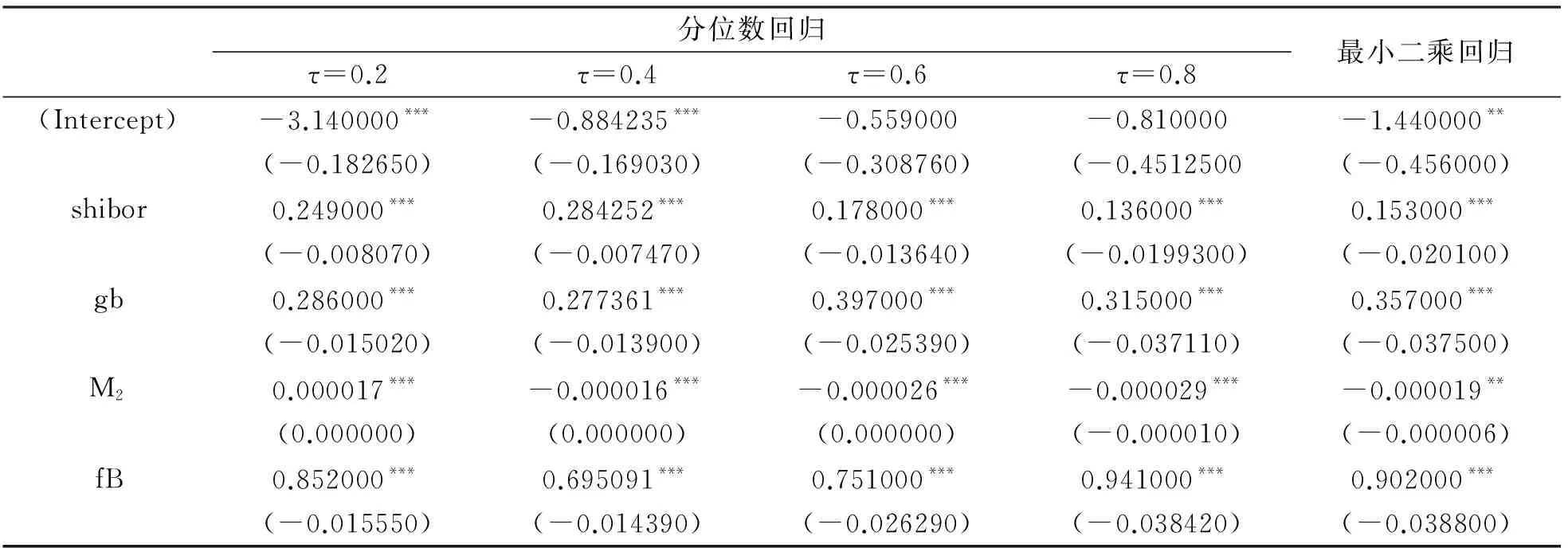
表3 分位数回归结果

注：(Intercept)表示常数项。

通过表3可以看出，分位数回归在部分分位数点上改变解释变量对被解释变量的影响方向，但是在一定程度上提高了解释变量的显著性，做最小二乘回归时货币供应量的在10%的显著性下显著，做分位数回归时排除了极端值对均值的影响，所以显著性大大提高，在5%的显著性水平下显著。从回归结果可以看出，上海银行间同业拆借率对余额宝7日年化收益率的影响是正向的，在其他变量保持不变的情况下，银行同业拆借率提高会让余额宝收益率也随之提高，国债收益率对余额宝收益率的影响也是正向的，在其他变量保持不变的情况下，国债收益率提高会让余额宝收益率也随之提高。货币供应量对余额宝收益率的影响在第低分位点是正向的，在0.4及以后的分位点上对余额宝收益率的影响是负向的。一年期银行理财产品收益率对余额宝的收益率的影响是正向的，在其他变量保持不变的情况下，一年期银行理财产品收益率提高会让余额宝收益率也随之提高。

从图3中可以看出，随着余额宝7日年化收益率分位数的增加，各解释变量对余额宝收益率的影响的变动趋势，上海银行间同业拆借率对余额宝收益率的影响基本呈U型，在余额宝收益率低分位点上同业拆借率对余额宝收益率的影响呈现下降趋势。国债收益率对余额宝收益率的影响呈现波动的趋势，但总体上是有上升的趋势。在余额宝0.8分位点之后同业拆借率对余额宝的影响呈上升趋势。货币供应量对余额宝收益率的影响随着余额宝收益率分为点的增加逐渐下降。银行理财产品收益率对余额宝收益率的影响是倒U型，在余额宝收益率的0.8分位点达到最大之后逐渐下降。

(四)基于贝叶斯分位数回归模型的建立

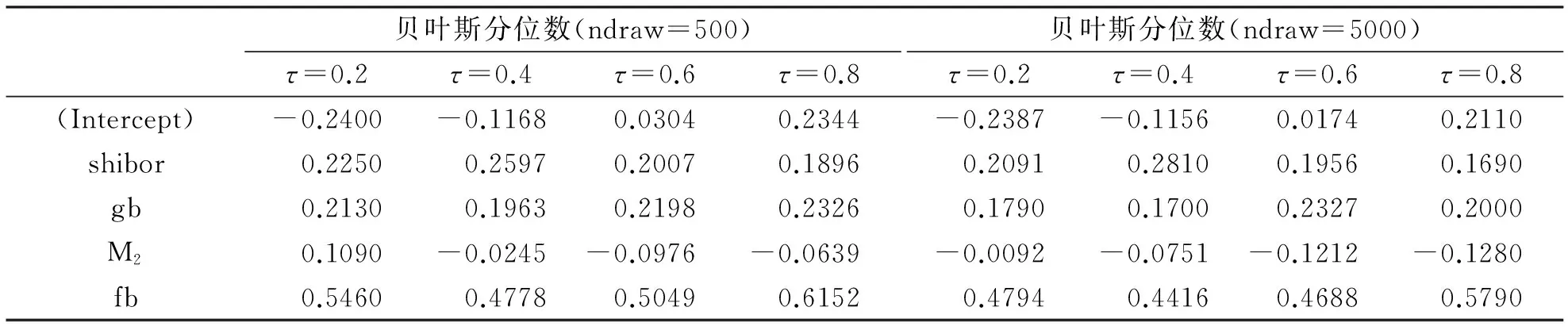
对分位数方法进行改进，利用贝叶斯分位数回归探究余额宝7日年化收益率与其影响因素之间的关系，实证结果见表4。

从表4可以看出上海银行间同业拆借率对余额宝7日年化收益率的影响是正向的，在其他变量保持不变的情况下，银行同业拆借率提高会让余额宝收益率也随之提高，且随着余额宝分位点的增加，银行同业拆借率对余额宝收益率的影响是逐渐减小的，与分位数回归略有差别。国债收益率对余额宝收益率的影响是正向的，在其他变量保持不变的情况下，国债收益率提高会让余额宝收益率也随之提高，在余额宝收益率的不同分位数点上，国债收益率对余额宝收益率的影响呈现波动的趋势，总体上是上升的，同时随着迭代次数的增加余额宝收益率各分位数上国债收益率对其影响的波动趋势消失，转为增长趋势。货币供应量对余额宝收益率的影响在低分位点是正向的，在0.4及以后的分位点上对余额宝收益率的影响是负向的，货币供应量对余额宝收益率的影响随着余额宝收益率分为点的增加逐渐下降。一年期银行理财产品收益率对余额宝的收益率的影响是正向的，在其他变量保持不变的情况下，一年期银行理财产品收益率每提高会让余额宝收益率也随之提高。银行理财产品收益率对余额宝收益率的影响随着余额宝收益率分位点的增加而逐渐增加。综合贝叶斯分位数的估计结果，该方法比单纯利用分位数的结果更加明显，趋势更加稳定。

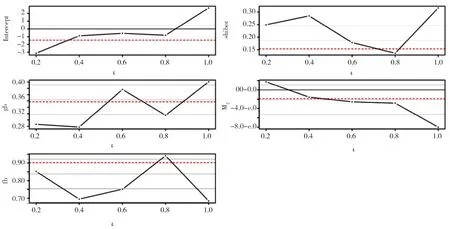
图3 不同分位点下估计系数趋势图

贝叶斯分位数(ndraw=500)τ=0.2τ=0.4τ=0.6τ=0.8贝叶斯分位数(ndraw=5000)τ=0.2τ=0.4τ=0.6τ=0.8(Intercept)-0.2400-0.11680.03040.2344-0.2387-0.11560.01740.2110shibor0.22500.25970.20070.18960.20910.28100.19560.1690gb0.21300.19630.21980.23260.17900.17000.23270.2000M20.1090-0.0245-0.0976-0.0639-0.0092-0.0751-0.1212-0.1280fb0.54600.47780.50490.61520.47940.44160.46880.5790

注：ndraw为迭代次数。

从贝叶斯分位数回归结果的置信区间表5中可以看出迭代次数与置信区间的宽度息息相关，随着迭代次数的增加，各解释变量的置信区间在逐渐减小，预测的精度越来越高。

利用贝叶斯方法对分位数回归进行估计，在得到参数之后可以通过做出变量参数的迭代轨迹图形来判断该系数是否收敛。以τ=0.2为例，做出贝叶斯分位数模型变量的迭代轨迹，见图4。

从贝叶斯分位数模型变量迭代轨迹中可以看出在τ=0.2的分位数水平下，贝叶斯分位数模型的参数估计值都相对集中，开始波动比较大，随着抽取次数的增加，系数逐渐趋于稳定，在一定范围来回震动。所以通过贝叶斯分位数模型参数估计的迭代轨迹图(图4)可以看出在余额宝收益率的τ=0.2的分位数下参数的迭代轨迹是收敛的。

(五) 模型结果分析

综上所述贝叶斯分位数模型最适合探究余额宝7日年化收益率及其影响因素之间的关系，同时通过增加迭代次数提高参数估计的精度。从实证结果可以看到，选取的4个解释变量上海银行间同业拆借率(shibor)、一年期国债收益率(gb)、一年期银行理财产品收益率(fb)、货币供应量(M2)对被解释变量余额宝7日年化收益率的影响是显著的，且每个解释变量在不同分位点上对余额宝收益率的影响方向基本稳定。其中货币供应量对余额宝的收益率的影响是负向的，其他解释变量对余额宝收益率的影响是正向的，说明宏观经济环境与余额宝收益率之间是反向关系，影响余额宝的资产投资收益率的因素与收益率之间是正向关系。

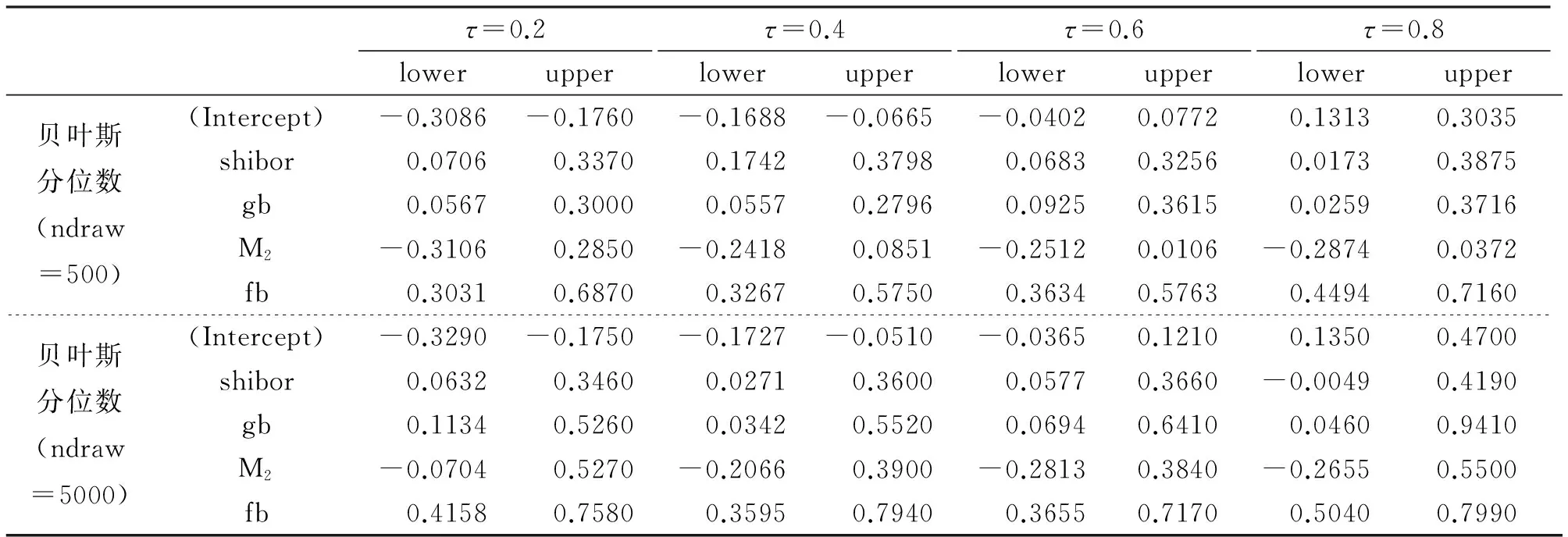
表5 贝叶斯分位数回归结果置信区间

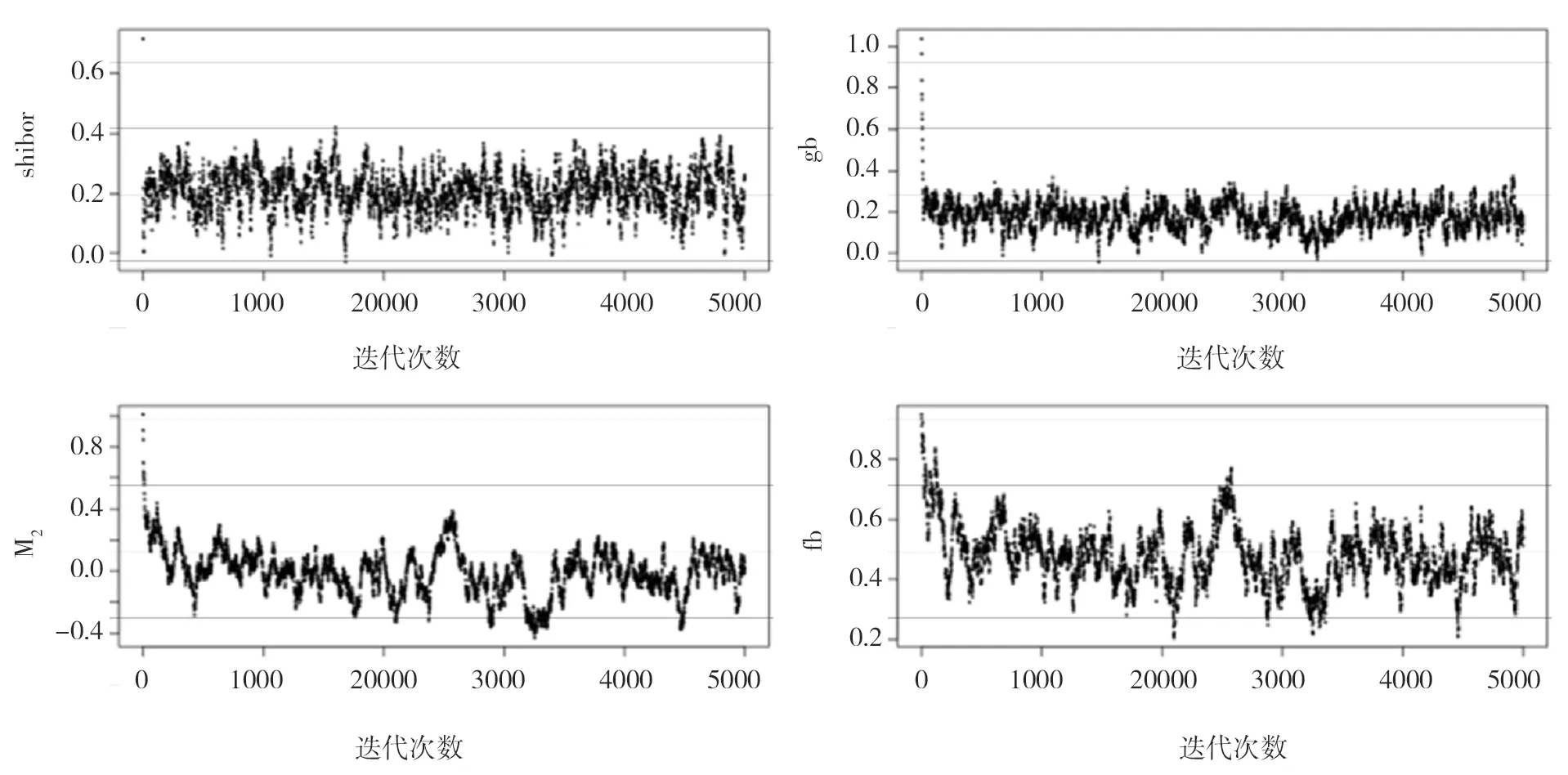
图4 贝叶斯分位数模型参数估计的迭代轨迹

四、余额宝的风险分析与政策建议

(一)余额宝的风险分析

通过对余额宝收益率及其影响因素之间的关系，分析余额宝可能面临的风险。

第一，根据贝叶斯分位数的实证分析结果可以看出在各分位点上影响余额宝收益率变动最大的因素是银行理财产品收益率，一年期的银行理财产品与余额宝一样具有流动性，当活期存款利率持续保持较低的状态时，余额宝会将原来投资银行存款的资金投资到理财产品上，当理财产品的收益率提高时，余额宝的收益率也相应的增加。但同时余额宝可能会面临着流动性风险，一年期的银行理财产品收益率要小于可以随时提现的余额宝，如果余额宝将大量资金投资于银行理财产品上将难以在短期套现，一旦面临大量客户同时提现，余额宝内的资金将难以周转。

第二，上海银行间同业拆借率作为利率的衡量指标，在低分位点对余额宝收益率的影响较大，在高分位点对余额宝收益率影响较小，说明在余额宝收益率低的时候起主要作用的是同业拆借率，在余额宝收益率较高的时候同业拆借率对余额宝收益率变动的影响减小，说明余额宝的高收益率并不是由银行业务带来的，反观一年期国债收益率，发现在低分位点对余额宝收益率的影响较小，在高分位点对余额宝收益率较大，这说明在余额宝收益率低的时候起主要作用的为同业拆借率，在余额宝收益率较高的时候起主要作用的为国债收益率，也就是说余额宝稳定的收益率是依赖于投资在银行的资产，而超过部分则由债券市场带来，债券市场的风险明显大于银行，所以会给余额宝增加投资风险。

第三，货币供应量对余额宝收益率的影响是负向的，且对余额宝收益率的影响在各分位点上逐渐增加，说明货币政策变化会使余额宝收益率发生反向变动，同时货币供应量的变化也可以作为宏观经济的指标，衡量市场上是否存在通货膨胀，货币供应量增加，通货膨胀率也会增加，在实际利率保持不变的情况下，货币供应量增加就相当于通货膨胀率的增加，名义利率会随着货币供应量的增多而减少，余额宝收益率与通货膨胀率呈负相关关系，即货币供应量的增加会给余额宝收益率带来反向作用。所以余额宝会面临市场风险，这种风险来自于市场本身，是由宏观因素决定，无法通过操作规避这类风险。

(二)政策建议

针对余额宝所面临的风险，提出以下建议。

第一，余额宝将过多的资金投资于银行理财产品而造成的流动性风险，可以通过限制其资金投入比例，按照占比设置投资额上限，首先可以将资金按照合理的比例投资在不同年限的银行理财产品中，其次可以将资金投资于其他安全系数高、流动性大的产品上，最终达到缓解流动性差的目的。

第二，针对余额宝在债券市场上面临的风险，天弘余额宝基金管理公司可以合理配置资金，优化自身的资产组合比，合理利用银行与债券市场的优势，利用银行投资作为其稳定收益的来源，债券投资作为其高收益的来源。

五、结语

笔者先从分位数回归入手对余额宝7日年化收益率及其影响因素建立分位数回归模型。发现上海银行间同业拆借率(shibor)、一年期国债收益率(gb)、一年期银行理财产品收益率(fb)、货币供应量(M2)这4个解释变量与余额宝收益率显著相关。

进一步利用贝叶斯估计的思想建立贝叶斯分位数模型，在5000次重抽样的基础之上，发现各解释变量在余额宝收益率的不同分位点上对余额宝收益率的影响趋势明显，银行理财产品收益率随余额宝收益率低分位点的增加对余额宝收益率的影响也越来越大，货币供应量正好相反，对余额宝收益率的作用是反向的，而且在余额宝收益率低分位点上影响最大，随着分位点的提高影响越来越小，同业拆借率在余额宝收益率低分位点上起作用更大，国债收益率在余额宝收益率高分位点上起作用更大。

通过研究发现在余额宝收益层面余额宝可能会面临着流动性风险和投资风险，以及市场风险，其中市场风险是由于宏观环境的变化造成的，余额宝很难通过对自身的改变减小风险，其他2个风险余额宝都可以通过优化资产组合比率、和优化资产组合项目来适当降低风险。

[1]王天宇.浅析“余额宝”对我国金融行业的影响[J].中国商贸,2014(1).

[2]郑椒瑾.互联网理财时代余额宝对商业银行的影响分析[J].中国市场,2014(31).

[3]刘晖,王秀兰,罗中华,李靖,张维.基于T+0模式的互联网金融产品研究——以余额宝为例[J].生产力研究,2014(2).

[4]陈川.余额宝高收益的经济基础[J].时代金融,2014(8).

[5]刘冬.互联网金融新模式之余额宝的发展与监管[D].华东政法大学,2014.

[6]李克穆.互联网金融的创新与风险[J].管理世界,2016(2).

[7]曾建光.网络安全风险感知与互联网金融的资产定价[J].经济研究,2015(7).

[8]周怡君.基于层次分析法的余额宝风险评价[J].全国商情(理论研究),2014(8).

[9]刘冬青.基于线性回归模型的余额宝价值分析[J].哈尔滨商业大学学报(社会科学版),2014(5).

[10]蒋玥.余额宝的收益影响因素以及风险分析[J].金融经济,2015(24).

[11]陆敬筠,薛卓之,周奇.银行同业拆借利率对余额宝收益率影响的实证研究[J].征信,2015(11).

[12]何建敏，白洁.基于EEMD-VAR的余额宝收益率影响因素研究[J].现代财经(天津财经大学学报),2015(8).

[13]陈耀辉，米盼粉.基于分数位回归模型的人民币汇率风险测度方法研究[J].长江大学学报(自科版)，2015(22).

责任编辑 胡号寰 E-mail:huhaohuan2@126.com

2017-03-28

国家社会科学基金项目(16BTJ030)

陈曜辉(1963-)，男，湖北天门人，教授，博士，主要从事金融数量分析研究。

F49;F832.2

A

1673-1395 (2017)03-0082-09