路基混凝土施工期温度应力影响因素敏感性分析

王军

（中铁十八局集团第一工程有限公司，河北涿州072750）

【建筑与规划】

路基混凝土施工期温度应力影响因素敏感性分析

王军

（中铁十八局集团第一工程有限公司，河北涿州072750）

针对路基混凝土施工期裂缝对路基稳定不利影响的问题，文章以汕（头）湛（江）高速公路云浮至湛江段及支线工程（化州至湛江段）第TJ-29合同段为研究对象，借助ANSYS有限元分析软件，结合工程实测资料以及以往建模经验，建立应力应变场仿真计算模型，系统地分析入仓温度、弹性模量两个因素对温度应力的影响。从分析结果来看：（1）混凝土结构的拉应力增长与温度变化呈指数正相关；（2）拉应力增长与弹性模量变化呈线性正相关；（3）混凝土入仓温度变化对于拉应力场的影响要远大于弹性模量变化引起的影响；（4）最容易形成裂缝的时间段为入仓2 d至5 d。

混凝土裂缝；入仓温度；拉应力；弹性模量;温度应力

作为道路工程的核心工程之一，路基的性能尤为重要，其结构的可靠性和耐久性，是相关部门和工程技术人员关注的焦点。路基结构体型和结构受力情况均十分复杂，极易在混凝土施工期出现裂缝[1]，裂缝会极大地影响了路基结构的防渗性、耐久性和结构强度[2]。目前虽然对路基结构混凝土的裂缝控制已探索出一些措施和方法，但是在建路基的表面、侧面仍然经常出现表观裂缝，对于路基混凝土施工期的裂缝控制的相关研究仍然很有价值。

美国麻省理工大学J.Rayller指出，路基混凝土在施工期产生裂缝的根本原因是因为混凝土表面拉应力超过其承载极限而产生的剪切塑性破坏，因此，要合理控制路基混凝土施工过程中的裂缝，就必须合理控制路基混凝土在施工过程中的应力分布[3~5]，其中，稳定应力是混凝土表面拉应力的重要组成部分。

本文以汕(头)湛(江)高速公路云浮至湛江段及支线工程(化州至湛江段)第TJ-29合同段为研究对象，借助ANSYS软件，结合工程实测资料以及以往建模经验，建立热力学仿真计算模型，系统地研究浇筑温度、弹性模量两个因素对路基混凝土施工期温度应力影响因素的敏感性。

1 施工期混凝土结构有限元计算模型

ANSYS有限元分析软件有较完善的APDL编程功能。本文利用ANSYS的APDL语言，采用参数化建模的方式建立了实例工程路基结构的热力学仿真计算模型。

1.1 计算网格划分

网格类型选择稳定性最好的三角网格，网格间距取5 m，对局部重点关心区域进行加密（网格间距取2 m）。网格划分后共有11 460个计算单元，23 150个节点。

1.2 初始条件、边界条件

计算模型的初始条件主要为混凝土的入仓温度，入仓温度数据来自于现场监测所得数据，现场监测时，每层混凝土入仓时均做一次监测记录，以监测记录作为入仓混凝土的初始温度。根据圣维南原理，在仿真计算模型范围足够时，路基混凝土的温度和外界的温度变化对于土层的影响很小，即土层的四周面和底面与外界可以认为没有热交换，因此将土层四周边界和底面设置为绝热边界。土层的上表面与外界接触，为散热边界条件。

1.3 发热源

混凝土施工期温度场发热源主要为内部的水化热产生，水化热函数采用朱伯芳院士[6]提出的三参数指数函数的形式：

其中:为待求参数，为混凝土的龄期，表示发热量。通常根据混凝土绝热温升试验获得。本报告计算模型中的水化热采用热生成函数施加

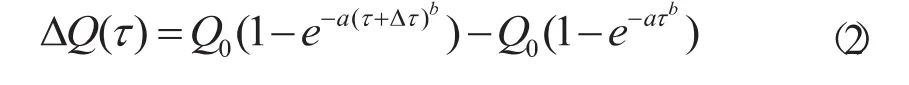
该式表示一个时间增量内由混凝土内部水化热产生的热量，其中三个重要参数通过参数反分析获得。

1.4 主要计算参数的选取

为保证数学模型计算精确性，应正确选择关键参数，主要包括混凝土抗拉强度、抗拉弹性模量、线膨胀系数、体积变形系数等等。本文采取试验测量法，共制作了10个混凝土试件，并采用与施工相同的养护方法，测定了试件组各项参数在1～28 d的平均值，并列于表1。

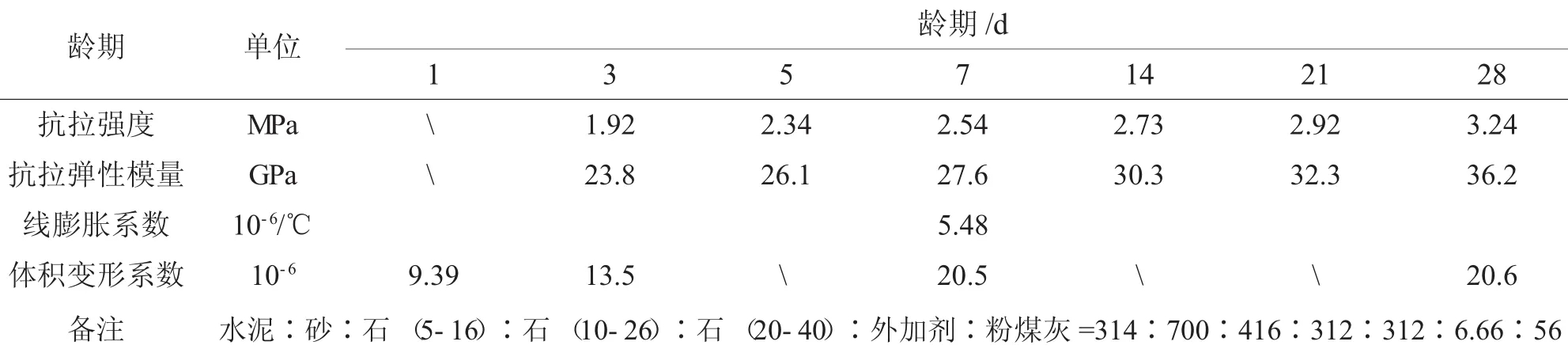
表1 混凝土主要参数率定结果

1.5 计算精度验证

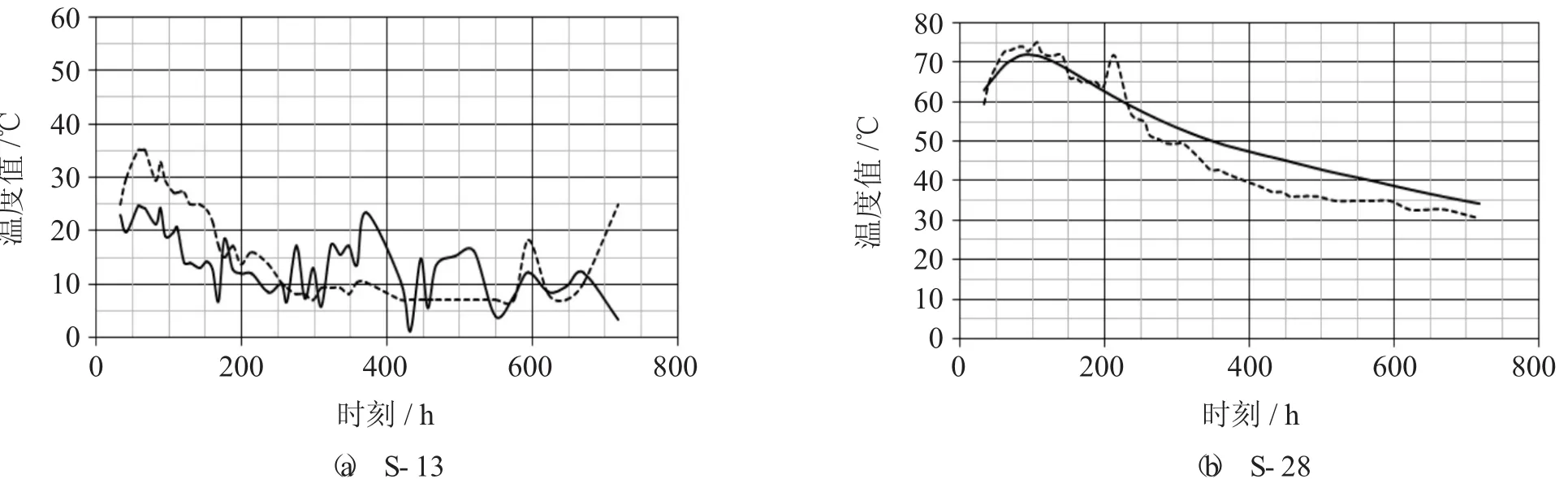
图1 特征点温度时程曲线预测结果

对实例工程施工期温度场进行了仿真计算，并与实测温度进行比较。计算精度来看，在实例工程53个测点共计1 865组数据中，共有1 367组数据（占数据总量的73.3%）计算值误差在5%以下，共有1 688组数据（占数据总量的90.5%）计算值误差在10%以下。可见根据热学参数反演分析所得模型计算值与实测值大部分点趋势较一致，能够很好地反映真实情况。将几个特征点S-13、S-28的温度时程曲线预测结果绘于图1。将S-13在5 d龄期和25 d龄期的切片云图分别绘于图2与图3。

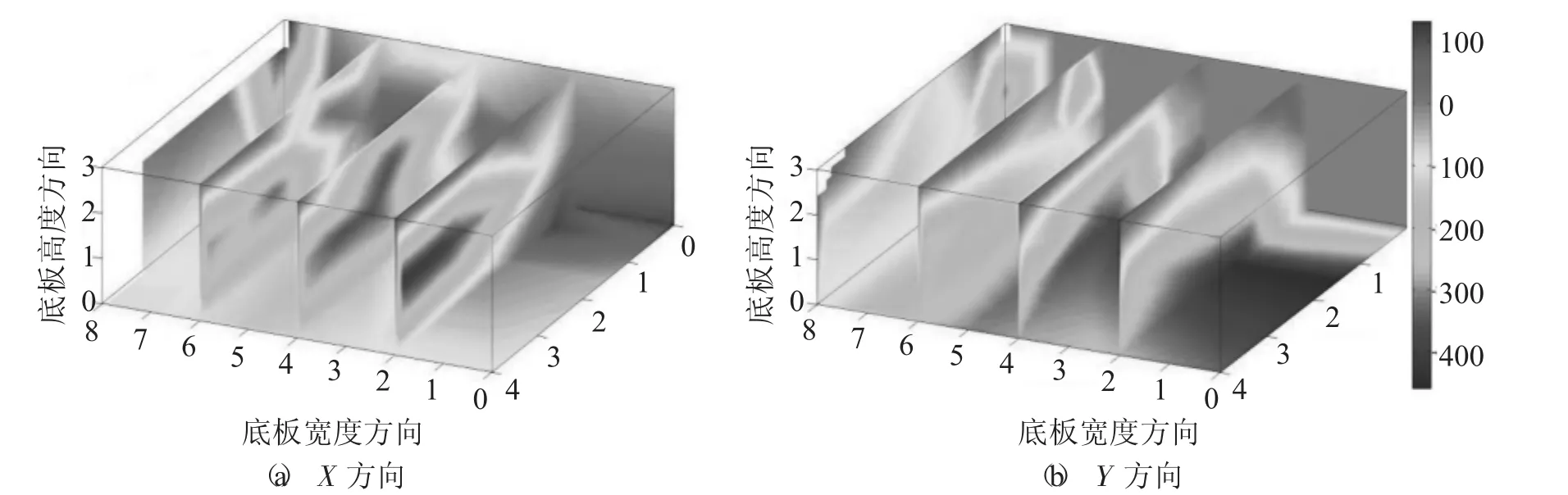
图2 5天龄期混凝土应变切片云图

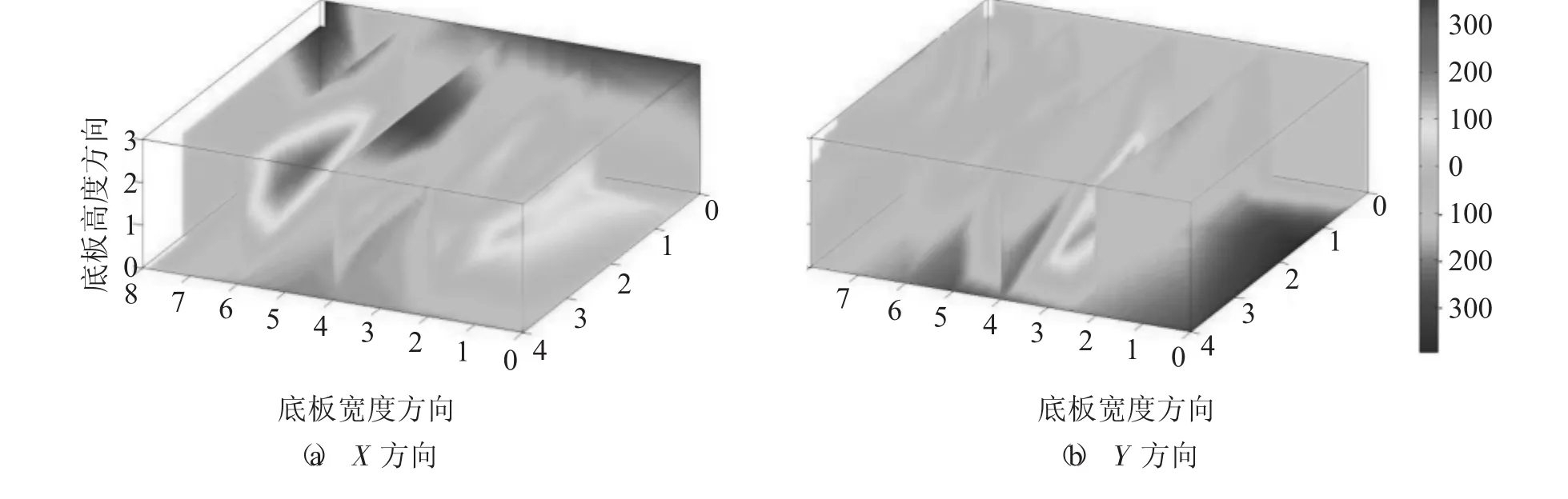
图3 25天龄期混凝土应变切片云图

2 因素敏感性分析

2.1 入仓温度敏感性分析

对于体型较大的混凝土结构，所谓温差应力对于早期混凝土结构应力场，特别是对拉应力场来说，具有重要影响作用。控制温差应力的关键是控制温差，而混凝土结构的外温受当地气候条件影响，基本不具有人工可控性，从温度控制的方面分析，在工程上可取的是控制浇筑温度和最高温度。

为了研究混凝土入仓温度对早期混凝土结构拉应力场分布的影响，以实例工程混凝土施工期仿真计算模型为研究对象，在其余条件（发热源、弹性模量、施工工序、混凝土养护条件等）不变的前提下，研究混凝土入仓温度的变化对应力大小的影响。该组试验以现场实测温度（21.6℃）为基准温度，考虑温度倍数变化（+25%、+50%、150%、0%、-25%、-75%，共计六组对比试验）对应力分布的影响。将试验计算结果列于图4与图5。

分析图4与图5可知：

（1）在入仓温度固定的情况下，混凝土拉应力变化可三维三个典型阶段，即迅速增长期（0～4 d）、逐渐回落期（5～18 d）以及逐渐稳定期（19～25 d）；

（2）对于入仓时间相同的混凝土，在其他条件不变的情况下，拉应力大小与入仓温度成正比。

（3）混凝土的入仓温度的大小是决定路基混凝土早期结构温度场的重要影响因素。

根据文献[11]，施工期混凝土温度最大值Tmax=入仓温度T0+水化热引起的温度变化△T，可见混凝土的温度峰值（该时刻达到最大拉应力）受入仓温度的重要影响，提高后者将会进一步增大混凝土内外温差。

同时，根据文献[12]给出的混凝土绝热温升函数：

式中为混凝土龄期，T为温度，a、b、c为常数。根据以上公式可以看出，绝热温升的变化曲线受即时温度的影响，因此，入仓温度的提高会使早期混凝土内部水化热更加剧烈，放热速率更高，易造成早期混凝土内部和外表面温差的进一步拉大。

（4）混凝土在入仓2 d至5 d时间段内，主拉应力较大，此时路基混凝土表面极易形成裂缝。

（5）在其他条件不变的情况下，拉应力增长与温度变化呈指数正相关。在不同入仓温度下，从拉应力对温度变化的敏感率来看，入仓温度越高拉应力的温度敏感性越高。在-75%基温下，拉应力的温敏变化率在0～33.6%范围内，而在+150%基温下，拉应力的温敏变化率范围可达0～54.8%。

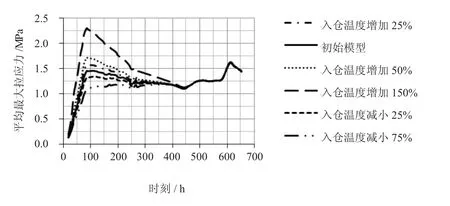
图4 平均最大拉应力时程曲线

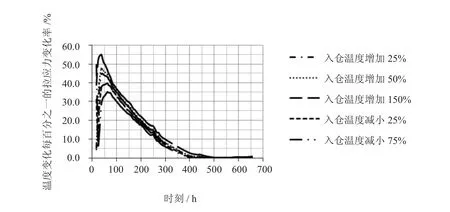
图5 温度每变化百分之一平均拉应力的变化率

2.2 弹模敏感性分析

为了研究混凝土弹性模量（即反映不同施工间隔时间造成刚度的差异）对拉应力的影响，以实例工程混凝土施工期仿真计算模型为研究对象，在其余条件（入仓温度、发热源、施工工序、混凝土养护条件等）不变的前提下，研究混凝土弹性模量的变化对应力大小的影响。对比试验共设置四组对比模型，分别以3 d、14 d、21 d、28 d的弹性模量作为试验参数，将试验分析结果绘于图6、图7。

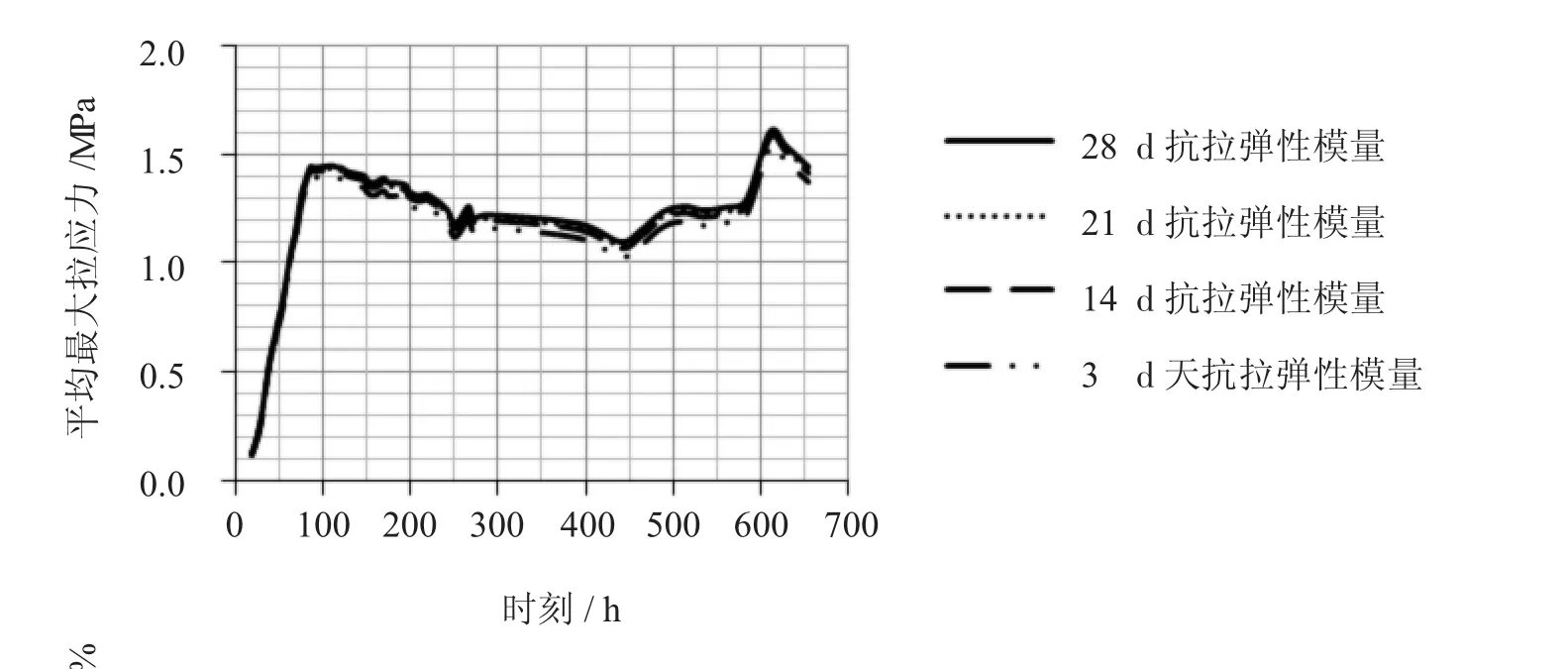
图6 平均最大拉应力时程曲线

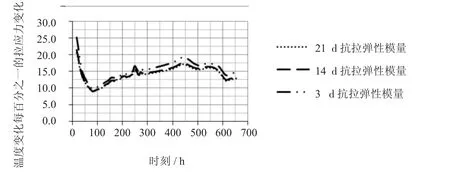
图7 弹性模量每变化百分之一平均拉应力的变化率

分析图6与图7可知：

（1）结构相对刚度理论上可以用弹性模量反映。由图6可以看出：随着结构相对刚度的减小，拉应力会逐渐减小，即在施工顺序、初始温度、水化热函数、边界条件等均不变的情况下，拉应力与相对弹模差值成正相关关系。但在不同弹模量下，拉应力时程曲线差异较小、较为类似。

（2）图7的纵坐标表示闸底板弹模以28 d抗拉弹性模量为基础，弹性模量每下降百分之一下拉应力的变化率。

（3）拉应力增长与弹性模量变化呈线性正相关。且在不同弹性模量下，拉应力对弹模变化的敏感性都比较相似，均在8.2%～24.6%的范围内。2.3敏感性对比

从上述分析结果来看：在不同入仓温度下，拉应力的温敏变化率在0～54.8%范围内；在不同弹性模量下，拉应力的弹模敏变化率则在8.2%～24.6%的范围内，结合图5与图7也可看出，前者的变化幅度要远高于后者。由此可见，拉应力场的温敏变化率要远大于弹模敏变化率。该结论反应到施工中即可认为，控制混凝土入仓温度，减小温差应力对改善拉应力分布的影响要大于控制施工间隔（增大结构相对刚度）的影响。

3结论

本文对路基混凝土应力应变场数值模型建立以及路基混凝土施工期温度应力影响因素敏感性进行了系统地分析，得到以下结论：

（1）在考虑几何造型、热学、结构荷载以及求解的边界条件和初始条件的基础上，借助ANSYS有限元软件建立了路基混凝土施工期底板结构的有限元计算模型。同时，借助MATLAB编制热学计算参数反分析的程序，反演分析算法采用遗传算法和有限元发，以绝热温升函数的参数和表面放热系数为反演对象，得到相关仿真计算参数。通过与实测值比较，证明本文模型计算值精度较高，能够很好的预测实际情况。

（2）混凝土在入仓2 d至5 d时间段内，主拉应力较大路基混凝土表面易形成裂缝。这段时期是混凝土养护的重点时期。

（3）以研究混凝土入仓温度对早期混凝土结构拉应力场分布的影响，结果表明：在发热源、弹性模量、施工工序、混凝土养护条件等条件不变的情况下，提高入仓温度会引起混凝土峰值温度大幅升高，从而产生更大的温差应力。且拉应力增长与温度变化呈指数正相关。

（4）通过调整弹性模量值来反映不同施工间隔时间造成刚度的差异，研究结构相对刚度对整个应力场分布的影响，结果表明：在其他条件不变的情况下；拉应力与相对弹模差值成正相关关系。但在不同弹模量下，拉应力时程曲线差异较小、较为类似。

（5）比较入仓温度敏感性及弹性模量敏感性，分析结果可以看出：拉应力场的温敏变化率要远大于弹模敏变化率。该结论反应到施工中即可认为，为了减小混凝土拉应力，改善拉应力分布，控制混凝土入仓温度，减小温差应力的效果要好于控制施工间隔（增大结构相对刚度）的效果。

[1]朱伯芳.大体积混凝土温度应力与温度控制（第二版）[M].北京：中国水利水电出版社，2012.

[2]李庆斌，卿龙邦，管俊峰．混凝土裂缝断裂全过程受黏聚力分布的影响分析[J]．水利学报，2012，43（1）：3l -36.

[3]KRAJCINOVIE D，SILVA M A G．Statistical aspects of the continuous damage theory[J]．International Journal of Solids and Structures，1982．18（7）：551-562．

[4]管俊峰，卿龙邦，赵顺波．混凝土三点弯曲梁裂缝断裂全过程数值模拟研究[J]．计算力学学报，2013，30（1）：143一155．

[5]PETERSSON P E．Crack growth and development of fracture zones in plain concrete and similar materials[R]．Division of Building Materials，ReportTVBM-1006，Sweden：Lund Institute of Technology，1981．

[6]吴瑶，徐世娘，吴建营，等．双K断裂准则在丹江口大坝安全性评定中的应用[J]．水利学报，2015，46（3）：366-372．

[7]管俊峰，卿龙邦，赵顺波．混凝土三点弯曲梁裂缝断裂全过程数值模拟研究[J]．计算力学学报，2013，30（1）：143一155．

[8]刘智光，陈建云，自卫峰．基于随机损伤模型的混凝土轴拉破坏过程研究[J]．岩石力学与工程学报，2009，28(10)：2048-2058．

[9]刘西拉，温斌．考虑应力边界条件的混凝土应变软化[J]．岩石力学与工程学报，2008，27（5）：885-892．

[10]赵志方．基于裂缝黏聚力的大坝混凝土断裂特性研究[D]．北京：清华大学，2004．

[11]王振红，朱岳明，武圈怀，等.混凝土热学参数试验与反分析研究.［J］，岩土力学学位论文，2009，30（6）: 1821-1826.

[12]徐芝纶.弹性力学（第四版）［M］.北京：高等教育出版社，2008.

（责任编辑：龙海波）

Sensibility of factors influencing temperature stress of roadbed concrete during construction period

WANG Jun

(The First Engineering Company Limited,China Railway 18th Bureau(Group)Co.,Ltd,Zhuozhou 072750,China)

The concrete cracks during the construction period can undermine the roadbed stability.In this study，with a practical road construction as the example，the author studied the effect of placement temperature and elasticity modulus on the temperature stress with a stress-strain field simulation and calculation model established with ANASYS.It was found that the increase of tensile stress was exponentially positively correlated with the change of temperature，while linearly positively correlated with the change of the elasticity modulus.The effect of the placement temperature on the tensile stress field was much larger than that of elasticity modulus.The cracks were most likely formed during the time from 2 days to 5 days after placement.

concrete crack；placement temperature；tensile stress；elasticity modulus；temperature stress

TU528.01

A

1673-4939（2017）02-0141-06

10.14168/j.issn.1673-4939.2017.02.12

2017-03-21

王军（1979-），男，甘肃天水人，硕士，工程师，研究方向：工程管理、项目变更索赔及市场开发。