中药浓缩用机械蒸汽再压缩系统模型与仿真*

汤添钧 刘成刚 肖聪 李伟华

（苏州科技大学环境科学与工程学院）（河北乐恒化工设备制造有限公司)

应用研究

中药浓缩用机械蒸汽再压缩系统模型与仿真*

汤添钧**刘成刚 肖聪 李伟华

（苏州科技大学环境科学与工程学院）（河北乐恒化工设备制造有限公司)

针对中药浓缩用机械蒸汽再压缩（MVR）系统，利用能量守恒式、压缩比与换热温差关系式、蒸汽压缩机特性曲线拟合式建立了系统的数学模型。以某中药制药企业的MVR系统为例，将数学模型求解值与实际测量值进行对比，发现模型求解精度较高，实际传热系数与压缩机总效率是造成模型误差的主要因素。对模型进行仿真，得到蒸发器传热系数下降后蒸发量与压缩比的预测值，对指导生产具有一定的意义。

中药浓缩 机械蒸汽再压缩 建模 仿真 蒸发器 传热系数 压缩比

随着经济的快速增长，我国正面临着严重的能源短缺问题。2013年医药制造业共消耗2 179.11万t标准煤[1]。作为中药制备中一项重要的耗能单元，蒸发浓缩工艺存在着蒸汽用量大、利用效率低等问题，具有较大的节能潜力。为提高蒸发浓缩工艺蒸汽的利用效率，多效蒸发（MED）技术已得到较为广泛的应用[2]。但与MED技术相比，一种设计合理的机械蒸汽再压缩（MVR）系统，具有蒸汽利用效率高、结构更为紧凑的特点[3]，目前已经进入国家重点节能技术推广目录。

在MVR系统中，利用蒸汽压缩机将蒸发出的二次蒸汽进行再压缩，使之重新成为热源加热物料，从而实现了二次蒸汽的全部回收[4]。在试验研究方面，文献 [5-6]测试了离心式与单螺杆式压缩机驱动的MVR试验台的蒸发能力；在实际工程应用方面，文献 [7-8]探究了MVR技术在工业含盐废水处理方面的节能效果。目前，MVR系统在中药浓缩领域的理论与应用研究，正逐步受到学者与制药企业的重视。

本文首先对中药浓缩用MVR系统建立数学模型，并实测了某中药制药企业提取车间MVR系统，然后将模型求解值与实际测量值进行对比，最后对数学模型进行仿真，得到传热系数下降后蒸发量与压缩比的预测值。

1 基于MVR的中药浓缩系统及数学模型

1.1 系统描述

适应于中药蒸发浓缩的特点，中药浓缩用MVR系统基本流程如图1所示，系统主要包含蒸汽压缩机、蒸发器、气液分离器、真空泵及其它辅助设备。

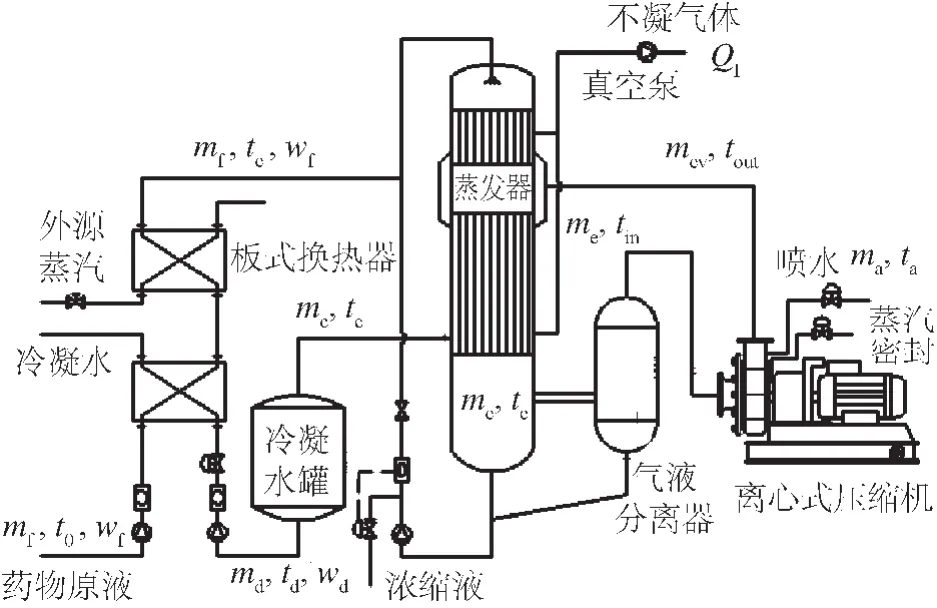
图1 MVR系统流程

蒸发流程为：物料罐中的药物原液由温度t0经两级预热至饱和温度te后进入蒸发器，在蒸发器管程内沸腾蒸发；气液两相流通过蒸发器下部的平衡管进入分离器中，气相被压缩机吸入，液相则通过分离器底部的管道返回蒸发器中。压缩后的过热蒸汽经喷水处理，变成同压力下的饱和蒸汽进入蒸发器壳程，放出潜热，最终进入冷凝水罐。由于冷凝水有较高的温度，使其进入预热器与原液换热，将热量传递给原液，从而完成蒸发流程。

系统中蒸汽热力过程见图2。当二次蒸汽从点A经过一多变过程压缩至点S时，其绝对压力上升，对应的饱和温度也相应上升。经过喷水处理消除过热，至饱和状态点B后进入蒸发器，热交换放出潜热后到达点C，回收的潜热量为图中阴影部分。蒸汽在压缩机进出口压力下对应的饱和温差Δt，即为MVR系统的换热温差。

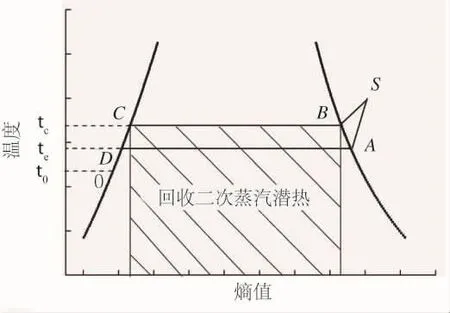
图2 蒸汽热力过程

1.2 系统数学模型

建立MVR系统数学模型遵从以下几点假设：

（1）忽略系统内的能量损失；

（2）二次蒸汽在蒸发器内完全冷凝；

（3）忽略物料浓度升高对沸点的影响。

1.2.1 系统能量守恒

在MVR系统中，蒸发器的常见形式为管壳式，将其简化成一个基本数学模型，其传热过程的计算式如下：

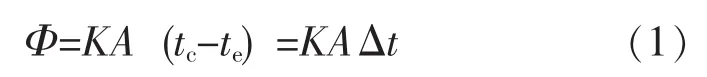
式中Φ——换热器换热量，kW;

A——换热面积，m2；

K——传热系数，kW/(m2·K)；

tc——蒸发器壳程饱和蒸汽温度，℃；

te——原液蒸发温度，℃；

Δt——换热温差，℃。

换热量的大小对压缩机的工作状态至关重要。压缩机处理的二次蒸汽量有限，蒸发出质量为me的二次蒸汽所需要的换热量为：

式中Φ——蒸发出二次蒸汽所需要的换热量,kW；

me——二次蒸汽蒸发量，kg/s；

Δhv——二次蒸汽潜热，kJ/kg。

在蒸发器中，传热系数的选择和计算较为复杂，影响因素较多，如换热器结垢、管壁磨损等，因此传热系数的大小对系统设计有较大影响。联列式（1）与式（2），可得到压缩机与蒸发器联合运行的能量方程：

式（3）表明，蒸发量与换热器的换热面积以及传热系数均成正比，与换热温差也呈线性关系。

1.2.2 压缩比与换热温差的关系

以水提取的药液为研究对象，在40～80℃温度范围内，水蒸气的饱和压力温度拟合曲线方程如下：

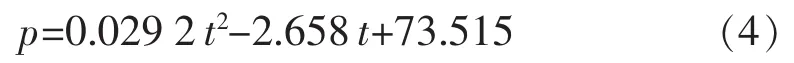
式中p——水蒸气饱和压力，kPa；

t——水蒸气饱和温度，℃。由于模型中忽略系统内的能量损失，因此原液蒸发温度与压缩机入口水蒸气温度近似相等（te=tin）。将水蒸气从pA压缩到pS，经过喷水处理后，压缩比与换热温差关系如下：

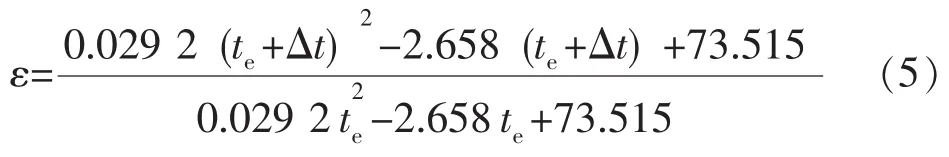
式中ε——压缩比。

若蒸发器所需的换热温差越低，压缩机提供的压缩比也就越小，同时需要的压缩功也就越低，对系统节能越有利。但是结合式（3）可知，换热温差减小后，为了提供足够的换热量，需增加换热面积或提高传热系数，二者一定程度上受到技术和成本的限制，因此，换热温差的取值对MVR系统的运行影响重大。

1.2.3 蒸汽压缩机特性

系统所需的压缩比是由蒸汽压缩机提供的，压缩机也是整个系统的主要耗能设备，压缩机的运行效果直接决定了系统的蒸发能力。某型号离心式蒸汽压缩机在12 800、14 400、16 000 r/min三个转速下的特性曲线如图3所示，式（6）为压缩比与流量的拟合关系式。

式中α、β、χ、δ——分别为拟合方程的系数；

ms、mc——分别为喘振点流量和堵塞点流量。

根据压缩机的多变效率曲线，可以计算出蒸汽压缩机的实际输入功率：

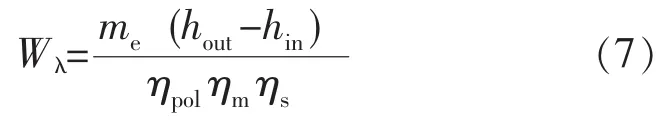
式中Wλ——压缩机输入功率，kW；

hout——压缩后水蒸气焓值，kJ/kg；

hin——压缩机入口水蒸气焓值，kJ/kg；

ηpol——压缩机多变效率；

ηm——传动效率，取0.75；

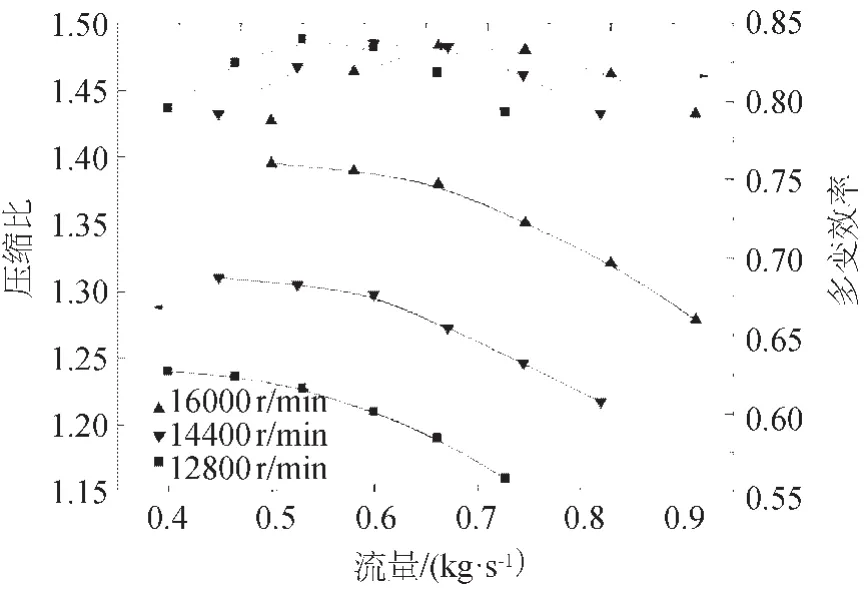
图3 离心式蒸汽压缩机特性曲线

ηs——电机效率，取0.9。

在MVR系统中，根据系统能量守恒、压缩比与换热温差关系、蒸汽压缩机特性曲线，可建立描述系统运行的数学模型：

对于MVR系统而言，在确定蒸发温度、压缩机与蒸发器特性参数后，方程组封闭，可求解出系统在不同工况下的蒸发量、压缩比、蒸发器换热量、压缩机输入功率等核心参数。

2 实例分析

以某中药制药企业蒸发浓缩工艺节能改造项目为例，对新增设MVR系统进行建模求解与测试。该系统的设计蒸发量为2880 kg/h，蒸发温度为70℃，系统选用离心式蒸汽压缩机（装机功率110 kW，特性曲线已确定），同时选择降膜式蒸发器，换热面积为210 m2，设计传热系数为1.50 kW/(m2·K)。

2.1 模型校核

MVR系统在原液预热、建立真空后，蒸发器中存在一定量的闪蒸蒸汽。启动压缩机，随着压缩机转速的提升，系统的蒸发量、压缩比将不断增加。利用数学模型求解出12 800、14 400、16 000 r/min三个转速下的蒸发量、压缩比、输入功率等参数的理论值，并与实际测量值进行对比。

图4中的曲线交点即为压缩机与蒸发器共同工作状态点，是三个转速下压缩机所需换热量曲线与蒸发器提供的换热量曲线的交点，也是数学模型的图形解。若图4中无曲线交点，则说明系统设计出现偏差，需重新选定蒸发器参数。求解出的计算值与实际测量值见表1。

从表1中的数据可以看出，由模型求解出的蒸发量、压缩比的理论值与实测值误差较小，而压缩机输入功率的误差则较大。系统测试运行中，压缩机转速提升至16 000 r/min，工况点A满足设计要求，此时实测蒸发量为2900 kg/h，压缩比为1.330，换热量为1 876.9 kW，压缩机电机输入功率为106 kW。

图4 压缩机转速对系统工况的影响

表1 各工况点计算值与测量值

造成误差的主要原因有：（1）中药提取液在循环泵的驱动下形成泡沫，增加了传热热阻，使传热系数低于设计值。（2）压缩机总效率实际值低于理论值。

2.2 模型仿真

系统经过一段时间运行后，蒸发器的壁面污垢厚度增加，传热系数降低。压缩机转速恒定于16 000 r/min，若蒸发器换热系数从1.50 kW/(m2·K)下降至0.74 kW/(m2·K)，应用数学模型仿真出传热系数下降后的情况如图5所示。

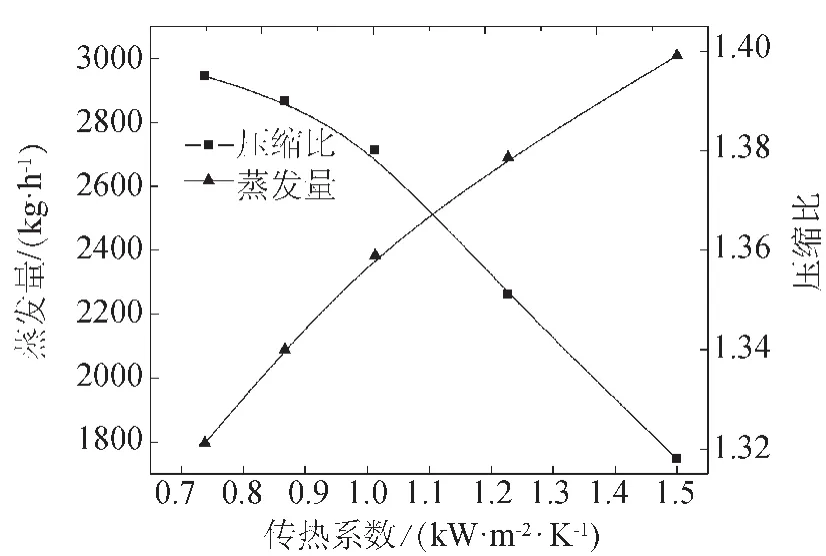
图5 传热系数对蒸发量、压缩比的影响

由图5中曲线可以看出，当传热系数下降后，蒸发量急剧下降，而压缩比却迅速上升，运行工况点会从点A沿压缩机特性曲线向右下方移动，并接近压缩机喘振点，系统运行将极不稳定。

由模型仿真结果可知，当传热系数下降50.7%后，蒸发量理论值从3008kg/h下降至1 796.4 kg/h，压缩比从1.318上升至1.395。在实际生产中，当转速达到设定的16 000 r/min，稳定蒸发量小于2000 kg/h或压缩比高于1.38后，应考虑对蒸发器列管进行清洗，以提高蒸发器传热系数，保证系统正常运行。通过对模型的仿真，预测出蒸发器传热恶化后系统的蒸发量与压缩比，对系统实际运行具有一定指导意义。

3 结论

（1）针对中药浓缩用机械蒸汽再压缩系统，利用系统能量守恒式、压缩比与换热温差关系式、蒸汽压缩机特性曲线拟合式建立了系统的数学模型。

（2）以某中药制药企业的MVR系统为例，将数学模型求解值与实测值进行对比，结果表明，该模型求解精度较高。传热系数与压缩机总效率是造成模型误差的主要因素。

（3）MVR系统测试运行中，压缩机转速提升至16 000 r/min后，实测蒸发量为2 900 kg/h，压缩比为1.330，换热量为1 876.9 kW，压缩机输入功率为106 kW，满足了设计要求。

（4）对数学模型进行仿真，得到传热系数下降后蒸发量与压缩比的预测值，对系统实际运行具有一定指导意义。

[1]中华人民共和国国家统计局.中国统计年鉴 [M].北京：中国统计出版社，2015.

[2]田荣海，陈国礼，吴俊生，等.五效蒸发装置模型与仿真 [J].华东理工大学学报，2000，26（5）：568-572.

[3]修允，陈岚，刘瑜凤，等.药用蒸馏水机基本传热结构性能分析 [J].中国医药工业杂志，2014，45（6）：577-581.

[4]顾承真，洪厚胜，张志强，等.罗茨压缩机驱动MVR热泵系统的实验研究 [J].化工进展，2015，34（6）：1602-1606.

[5]庞卫科，林文举，潘麒麟，等.离心风机驱动机械蒸汽再压缩热泵系统的性能分析 [J].机械工程学报，2013，49（12）：142-146.

[6]王力威，庄景发，杨鲁伟，等.单螺杆水蒸气压缩机驱动的MVR系统性能实验研究 [J].中国科学院大学学报，2015，32（1）：38-45.

[7]李清方，刘中良，庞会中，等.基于机械蒸汽压缩蒸发的油田污水脱盐系统及分析 [J].化工学报，2011，62（7）：1963-1969.

[8]唐文骞，杨同莲，宋冬宝.机械蒸汽再压缩技术在钛白黑钛液浓缩中应用[J].化学工程，2015，43（9）：21-24.

Model and Simulation of Mechanical Vapor Recompression System for Concentrated Traditional Chinese Medicine

Tang Tianjun Liu Chenggang Xiao Cong Li Weihua

Aiming at the mechanical vapor recompression(MVR) system for concentrating traditional Chinese medicine,the mathematical model of the system is established by means of the formula of energy conservation,compression ratio and heat transfer temperature difference,and the fitting of the characteristic curve of the steam compressor.Taking an MVR system of a Chinese pharmaceutical enterprise as an example,the mathematical model is compared with the actual measured value,and it is found that the accuracy of the model is higher.The actual heat transfer coefficient and the total compressor efficiency are the main factors causing model errors.The model is simulated,and then the predicted value of evaporation and compression ratio is obtained after the evaporator heat transfer coefficient is decreased,which has certain significance for guiding production.

Chinese traditionalmedicine concentrate;Mechanicalvaporrecompression;Modeling;Simulation;Evaporator;Heat transfer coefficient;Compression ratio

TK 11+5

10.16759/j.cnki.issn.1007-7251.2017.06.006

2016-10-10)

*镇江市经信类专项资金扶持节能与循环经济项目（镇经信[2015]103号）。

**汤添钧，男，1992年生，硕士。苏州市，215009。