拐折断层地震活动性研究进展

张增换，马晓静，王 时

河北地质大学 a. 研究生学院、b. 资源学院，河北 石家庄 050031

拐折断层地震活动性研究进展

张增换a，马晓静b，王 时a

河北地质大学 a. 研究生学院、b. 资源学院，河北 石家庄 050031

论文从拐折断层地震活动性特征、断层黏滑运动的岩石物理实验和数值模拟实验角度分析总结了拐折断层的发震特征与发震机理。对实际震例的监测与野外观测结果表明：拐折断层的角度和拐点对地震的发生、震级的大小、断层的破裂方向有重要影响，而室内的实验研究表明断层带内的物质成分、断层的摩擦系数、应力扰动等因素对断层黏滑运动特征有很大影响。作为自然界普遍存在的断层形式，拐折断层的黏滑运动特征及其影响因素的研究有助于我们了解地震的发生机理，在未来的研究中应进一步加强。

拐折断层；地震活动性；黏滑运动；数值模拟

一、引言

地震会给人民的生命财产造成重大损失，而浅源地震的危害尤为严重。目前，地震预测模型及其形成、发展的标志性可定量要素尚未找到[1]。而地震发震机理的研究是地震预测的前提，断层的黏滑运动作为大震发生的一种机制已被越来越多的人接受。然而自然界的断层面很少以简单连续的面状结构出现，通常都表现为复杂的断层带，大多是不连续结构，例如拐折断层、雁列式断层、阶步式断层、分支断层等[2]。这些特殊的构造形式对断层应力集中、应变分配、断层滑动以及地震孕育发生及破裂的传播过程有重要影响。许多震例表明断层的拐折部位对地震活动起着至关重要的作用，因此对拐折断层黏滑运动过程的研究具有重要的理论意义和现实意义。

本文首先总结了拐折断层的地震活动特征与导致其发生的原因，对发震机理——断层的黏滑运动相关研究进行了分析。阐述了拐折断层的地震活动特性、拐折断层的地震前兆位置、拐折断层的破裂特征特征、断层黏滑活动的影响因素。同时也分析了物理研究方法与数值模拟方法的优势与局限性。并建议未来研究方向应为有更适用地学研究的物性参数并涉及多物理场的数值实验，以及有更先进仪器设备和更合理的观测手段的物理实验室研究，以便为强震发生的机制提供更多的理论基础。

二、拐折断层的地震活动性特征

地震的发生大多是先存断裂的活化，实际震例表明，许多强震大都发生在拐折断层上。例如，在San Andreas大断裂分别于1690年、1630年和1857年发生的三次地震均位于大拐折的附近；1975年、1976年分别发生于土耳其的Lice与Caldiran地震和1976年发生在唐山大地震同样为拐折断层的活动；而1989年发生在Loma Prieta的地震和1994年发生在Lander的地震以及1999年发生在Izmit的地震也发生在断层的拐折附近[3-4]；类似的是2002年发生在Denali断层上的地震和1976年发生的危地马拉地震亦发生于拐折断层活动带上；2008的汶川地震也与拐折断层相关。

（一）拐折断层地震特征

Kato[5]的实验结果发现拐折断层的动力学破裂属于“双震型”，而事实上确实如此，例如，2006年发生在日盐津县豆沙镇的两次5.1级地震，两次地震均位于NE向断裂的同一构造区，这次双震型地震被认为是由于障碍体存在而导致的[6]。云龙[2]的实验结果表明单拐折断层的失稳事件往往是时间相隔很短的双震事件，而压性双拐折断层的失稳事件往往由时间间隔较长的两次事件组成。Kato[5]提出拐折断层的两次破裂受主压应力夹角的控制，低角度破裂早于高角度，且始于低角度的破裂终止于拐点，而始于高角度的破裂则贯穿整个断层，也可以说拐折部位正应力场的变化控制着破裂的起点和终点。而初始剪应力、正应力的分布影响着拐点处的破裂速度[7]。然而，双震的发生时间间隔因实验中应变与观测手段等的差异并不相同，例如kato等[5]的结论是10.8ms-3.5s，而郭彦双等[8]的实验结果则是100ms-200ms。此外，马瑾[9]通过拐折断层的温度场实验研究也同样观测到双震甚至多震而引起的温度场变化，并提出下断层先错动，上断层后错动，两者的时间间隔为0.92s，拐折角度、岩石厚度、岩石类型等条件的不同都会对双震的时间间隔有影响。

“双震型”这一特点的原因或许可以归为拐点的控制作用，而Kato[5]认为速度状态基础可能是破裂延迟的原因。郭伶俐[10]研究了三种典型断层的失稳瞬态过程，认为拐折断层的拐点在断层的活动中起到类似枢纽的作用，这一点与马瑾[11]的实验结论是相同的。正是因为拐点的控制，导致区域的应变积累和积累后的急剧释放，引起多点错动，从而致使拐折断层多为双震或者多震。此外，这种断层错动势必造成断层几何发生变化，甚至导致新断层的产生及引起区域应力场的重新分布，进而使得断层运动形式发生新的变化。Andrews[12]认为断层的拐折部位对断层错动具有抑制作用，致使拐点两侧断层的位移量产生差异，当走向上的变化剧烈时，将会产生新的断层，这应该是拐折断层多发育强震的原因。

（二）拐折断层的破裂过程

Kase等[7]根据拐折部位能否抑制断层的错动，将拐折体分为抑制型拐折(Restraining bend)和松弛型拐折(Releasing bend)，并提出拐折对破裂的传播有非常重要的作用，拐折附近的位错速度受破裂导致的应力变化控制。在San Andreas的Parkf i eld段上的多次地震的震中都在一个拐折断层的拐点附近，这些地震的前震分布在拐点的西北段，主震则开始于拐点的附近，而余震位于转折部位的南东段[13]。Custódio[14]通过对在San Andreas的Parkf i eld段上1966年和2004年的地震的研究指出两次地震破裂的传播方向是相反的。马瑾[11]通过对5°拐折断层的物理实验和数值模拟结果表明：大事件并未发生在拐折位置而是发生在两侧的平直断层位置，并认为拐点起到阀门似的作用。可见，有些地震的震中位于拐折附近，破裂向拐折的一侧或同时向两侧传播。但也有些地震震中位于拐折两侧的平直断层上，这可能与拐折处障碍体的不完全破裂有关，当障碍体全部破裂后大震才会发生，这与马瑾[9]通过实验研究5°拐折断层温度场演化得出的结论是一致的。

（三）拐折断层的角度

与强震相关的拐折断层多为低角度(5°～30°)，例如，1992年发生在美国Landers的大地震圣安德列斯断层的拐角大约为18°，而与唐山大地震相关的郯庐大断裂不同段的拐折角度最大也只有25°，而更多与强震相关的拐折断层为接近平直的小角度拐折[11]。King等[15]通过对大量拐折断层带的研究，提出很多强震存在于两个5°拐折断层之间。目前大多学者认为在断层带上的5°拐折区域对震源位置、断层破裂传播过程、前震和余震分布及位错分布有重要影响，所以许多实验室研究采用了这一角度。而强震多发育于低角度拐折断层的原因可能是因为低角度对破裂的传播阻碍较小，断层间更容易发生较强烈的相互作用。然而，不同拐折角度的对比研究并没有学者分析。

（四）拐折断层的地震前兆

野外观测结果显示断层拐折处通常破裂非常复杂，拐折断层段上在一定范围内位移量大小与离拐点的距离成反比[12]，所以通常认为拐点处的前兆观测非常重要。马瑾[16]在研究不同构造部位在变形中的作用时，指出前兆并不一定出现在发震区域，会出现前兆偏离的现象。断层几何结构对地震前兆有重要影响，几何结构愈复杂，参与失稳过程的构造部位愈多，则前兆种类愈多，现象愈复杂。而其他学者在对比研究平直断层与几何弯曲断层时也得出了相似的结论[17]。郭彦双等[8]、云龙[2]则提出观测的方式方法不同所得出前兆响应也存在差异。马瑾[9]以5°拐折断层一次粘滑事件中不同变形阶段的温度场演化为例,分析了进入亚失稳状态时应力随时间的变化状态等问题，提出亚失稳到失稳阶段占整个时间比例不到1%。

三、断层黏滑运动的实验室研究

一些学者在断层黏滑运动的影响因素方面做了很多探讨，例如断层间物质对黏滑运动的影响，不同滑动方式会在实验产物中留下不同的显微结构，吕广廷[18]等认为断层泥的均匀性与非均匀性是断层发生蠕滑和黏滑的直接微观证据；断层泥中水的含量对断层黏滑运动有一定的影响，化学角度上水的存在增加了其稳定性，而力学角度上水的存在则起到了相反的作用[19]。近年来，随着相关研究的不断进行，断层滑动失稳的成核、均匀与非均匀断层黏滑运动中应变以及断层位错的实验研究等也为许多学者所关注[20]。有的学者通过实验研究认为断层黏滑的动态活动时间很短且运动由高速与低速交错组成[21]，并且加载速率与粘滑事件的周期长短呈负相关，而与应力降呈正相关[8]。黄元敏等[22]认为剪应力扰动是影响断层黏滑运动的推动力，而正应力扰动则导致断层接触状态的改变，所以正应力扰动较剪应力对断层黏滑运动的影响大。缪阿丽[23]以硬石膏和岩盐等作为断层泥材料，通过双轴摩擦实验研究了摩擦滑动的速度依赖性转换，解析了断层物质的微观结构及相关地震机制意义。上述的物理实验室研究虽不完全是以拐折断层为模型，但是其影响因素对拐折断层黏滑运动的影响也是类似的。

大多数物理实验室研究是通过岩石实验的方法，所选用的岩石多为上地壳分布最广的花岗岩类，使用伺服压机等对样本进行实验并利用声发射、应变片等物理手段进行研究。关于拐折断层的研究多为某一单拐折或双拐折构造在一次粘滑事件中变形过程及相应的物理场。本文对比了拐折断层主要的物理实验研究，如表1所示。然而，目前的许多研究是某个粘滑过程中各种物理场的演化过程，缺乏与多个粘滑过程引起的应变场的差异的对比研究，且缺乏不同拐折角度的对比研究。此外，实验研究与野外实测资料的对比分析也是很有必要的。

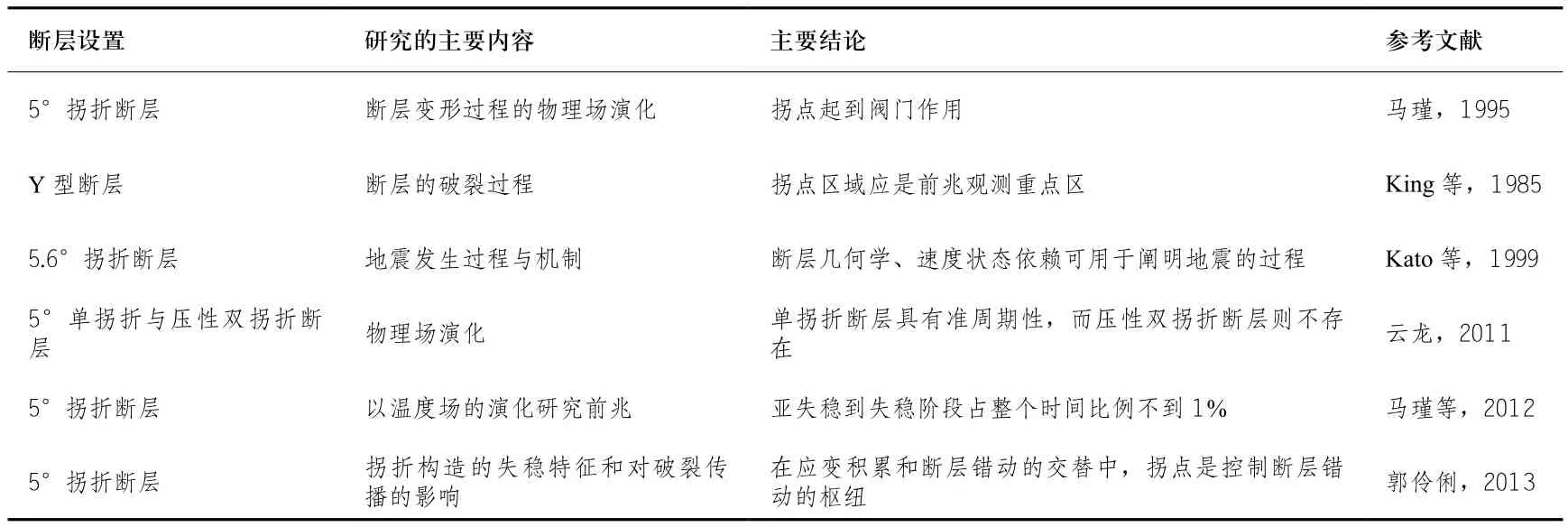
表1 部分典型拐折断层物理实验类比表

四、断层黏滑运动的数值实验研究

边界元法、有限元法、有限差分法等是主要的数值模拟方法。边界元方法广泛应用于各种断层的黏滑过程模拟研究[24-25]，它可以采用不同摩擦定律，也可以引入断层的非均质性。而有限元通常被认为是适用更加广泛的一种方法[26]。此外，拐折断层的处理方法主要有两种，一种是把整个模型处理成一个连续体，把断层设置为软弱地带；另一种是把整个几何模型设置为2个接触的模型，通过接触分析计算断层间的非线性关系。

事实上，数值模拟的方法正在越来越多的应用在地震危险性与预测的相关研究中。Sasani[27]通过对区域应力分布的计算来评估区域地震危险潜力。马晓静[28]通过数值模拟研究了拉伸速率、摩擦系数、正断层倾角对断层黏滑运动的影响，大震发震间隔随拉伸速率（＜5mm/a时）增大而变短，摩擦系数越小（＞0.4时），发震间隔越短，倾角大约60°时，断层发震最强烈。姜辉[29]模拟研究了太平洋板块俯冲带上的断层黏滑运动过程，分析了俯冲带地震的发生模式以及俯冲角度的影响，有角度变化的模型发生的黏滑事件较多。Cruzatienza等[30]利用边界积分方程法（BIEM）求解动力问题以探讨拐折断层的影响，强调了节点处剪切应力降分析的重要性。焦明若[31]利用RFPA-2D分析了岩石的均质程度对其破裂程度以及微震序列的影响，并提出不同均质程度发育不同的地震序列类型。虽然基于拐折断层的数值模拟研究有限，如表2所示，但也是目前很有前景的研究方法，而参数的设置应有更多适用地球科学研究的改进。薛霆虓[17]利用有限元法模拟了二维弹性介质的弯曲断层，并从前兆和余震、能量释放、发震周期等方面与平直断层进行了对比，认为弯曲断层由于抑制了地震活动的频率而更易导致大震的发生，且弯曲断层的前兆较平直断层明显。Xing等[32]通过有限元模拟提出拐折断层大多是“双震型”。王学滨[33]通过对FLAC-3D编程开发，统计分析了Z字形复杂拐折断层系统中不同断层带上与剪切、拉伸相关的6种量的时间演变规律，同样得出位于标本两侧的拐折断层和平直断层交替活动，而触发下一条平直断层的活动并导致整个系统的失稳。

孙楠[34]利用数值模拟的方法分析了正应力、静态应力扰动及动态应力扰动等对断层黏滑运动的影响。王学滨[27]从数值模型的角度分析了实验室尺度摩擦弱化、摩擦强化-摩擦弱化两种模型（Wang等，2012,2013），前者适用于破坏和前兆的模拟，后者适合于断层黏滑，并指出实验室尺度模型的模拟有助于充分了解计算模型的特点及优劣。近期，Barbot等[35]国外学者使用数值模拟的方法研究了断层黏滑运动及主震、同震、震间、震后等现象；黏滑运动发生的时间间隔、长期以及短期现象的数值模拟也取得一定的研究成果[36-37]，这些成果无疑给地震的预测与研究提供了新的思路。伴随着对地球动力学更深入的认知，数值模拟技术正在发挥着越来越重要的作用[38]。因此拐折断层黏滑运动过程的研究尤其是数值研究方面是未来地震机理研究的一个重要方向。

五、小结

拐折断层地震活动性目前的研究已经很多，但缺乏完整而系统的研究。作为自然界最普遍存在的一种断层形式，拐折断层黏滑运动过程无论是实验室研究还是数值模拟研究都需要进一步加强。

（一）方法的优势与局限性

实际震例的研究为地震活动研究提供真实直接的证据，但由于地震的突发性，观测手段的局限性，我们很难在野外直接观测到断层的黏滑运动。

实际测点往往反映的是断层附近某些点的物理场，难以反映整个区域整体场的情况，相对而言实验可以通过现有的技术方法观测研究模型整体不同场的变化特征，对于研究拐折断层的活动特征提供很多科学数据。然而，大多数实验室研究是有其不足之处的，例如，实验室研究岩石类型单一，受实验仪器和观测及采样速率的影响等。

表2 部分典型拐折断层数值实验类比表

数值模拟的方法可以弥补以上不足，数值模拟断层效应从尺度和效应上更接近于真实断层的活动，并且经济快捷，各种参数提取方便，可以方便地开展参数的敏感性研究，模拟在当前技术条件下无法开展的物理实验，计算更加定量化和可视化。然而参数的选取和模型的设置存在随意性，并不能完全符合实际地质情况，所以更适合地学研究的物性参数和模型设置都有待进一步改善。

（二）展望

拐折断层系统破坏以及黏滑运动过程的综合研究，无论从力学方面还是地质学方面都是一个相当复杂的过程。无论是实验室研究还是数值模拟研究都与科技的进步密切相关，更高采样速率的观测仪器与更先进的软硬件计算机设备都会为研究提供更好的平台。展望未来的研究应是有更适用地学研究的物性参数并涉及多物理场的数值实验，以及有更先进仪器设备和更合理的观测手段的物理实验室研究，以便为强震发生的机制提供更多的理论基础。

[1] 滕吉文. 强烈地震孕育与发生的地点、时间及强度预测的思考与探讨[J]. 地球物理学报, 2010, 53(8)： 1749-1766.

[2] 云龙, 郭彦双, 马瑾. 5°拐折断层在黏滑过程中物理场演化与交替活动的实验研究[J]. 地震地质, 2011, 33(2)： 356-368.

[3] SCHWARTZ S Y, ORANGE D L, ANDERSON R S. Complex fault interactions in a restraining bend on the San Andreas Fault, southern Santa Cruz Mountains, California[J]. Geophysical Research Letters, 1990, 17(8)： 1207-1210.

[4] AOCHI HIDEO, RAÚL MADARIAGA, EIICHI FUKUYAMA. Effect of normal stress during rupture propagation rupture along nonplanar fault[J]. Journal of Geophysical Research, 2002, 107(B2)： ESE5-1-ESE5-10.

[5] KATO N, SATOH T, LEI X, et al. Effect of fault bend on the rupture propagation process of stick-slip[J]. Tectonophysics, 1999, 310(1)： 81-99.

[6] 叶建庆, 陈慧, 刘学军, 等. 2006年云南盐津5.1级双震的监测与研究[J]. 地震研究, 2008, 31(2)： 134-141.

[7] KASE Y, DAY S M. Spontenous rupture processes on a bending fault[J]. GEOPHYSICAL RESEARCH LETTERS, 2006, 33：L10302.

[8] 郭彦双, 马瑾, 云龙. 拐折断层黏滑过程的实验研究[J]. 地震地质, 2011, 33(1)： 26-35.

[9] 马瑾, S I SHERMAN, 郭彦双. 地震前亚失稳应力状态的识别——以5°拐折断层变形温度场演化的实验为例[J]. 中国科学：地球科学, 2012, 42(5)： 633-645.

[10] 郭玲莉, 刘力强, 马瑾. 黏滑实验的震级评估和应力降分析[J].地球物理学报, 2014, 57(3)： 867-876.

[11] 马瑾, 马文涛, 马胜利, 等. 5°拐折构造变形物理场的实验研究与数值模拟[J]. 地震地质, 1995(4)： 318-326.

[12] ANDREWS D J. Fault geometry and earthquake mechanics[J]. Annals of Geophysics, 1994, 37(6)： 79-86.

[13] HILLERS G, BEN-ZION Y, MAI P M. Seismicity on a fault controlled by rate-and state-dependent friction with spatial variations of the critical slip distance[J]. Journal of Geophysical Research Atmospheres, 2006, 111(B1)： 997-999.

[14] CUSTÓDIO S, ARCHULETA R J. Parkfield earthquakes：Characteristic or complementary?[J]. Journal of Geophysical Research Atmospheres, 2007, 112(B5)： 622-634.

[15] KING G C P, NABELEK J F. Role of fault bends in the initiation and termination of earthquake rupture[J]. Science, 1985, 228： 984-987.

[16] 马瑾, 马胜利, 刘力强, 等. 断层几何结构与物理场的演化及失稳特征[J]. 地震学报, 1996, 18(2)： 200-205.

[17] 薛霆虓, 傅容珊, 林峰. 几何弯曲断层活动性的模拟[J]. 地球物理学报, 2009, 52(10)： 2509-2518.

[18] 吕广廷, 汤泉, 赵广堃. 断层泥在粘滑机制中的作用[J]. 国际地震动态, 1983(2)： 18-21.

[19] 黄建国, 张流. 水对断层摩擦滑动稳定性的影响[J]. 地震地质, 2002, 24(3)： 387-399.

[20] MA S, LIU L, MA J, et al. Experimental study on nucleation process of stick-slip instability on homogeneous and nonhomogeneous faults[J]. Science China Earth Sciences, 2003, 46(2)： 56-66.

[21] 宋义敏, 马少鹏, 杨小彬, 等. 断层黏滑动态变形过程的实验研究[J]. 地球物理学报, 2012, 55(1)： 171-179.

[22] 黄元敏, 马胜利, 缪阿丽,等. 正应力扰动对断层滑动失稳影响的实验研究[J]. 地球物理学报, 2016, 59(3)： 931-940.

[23] 缪阿丽. 几种模拟断层泥摩擦滑动速度依赖性转换的实验研究[D]. 北京： 中国地震局地质研究所, 2011.

[24] LAPUSTA N, RICEJ R, BEN-ZION Y, et al. Elastodynamic analysis for slow tectonic loading with spontaneous rupture episodes on faults with rate- and state-dependent friction[J]. Journal of Geophysical Research Atmospheres, 2001, 105(B10)： 23765-23789.

[25] BIZZARRI A, COCCO M, ANDREWS D J, et al. Solving the dynamic rupture problem with different numerical approaches and constitutive laws[J]. Geophysical Journal International, 2010, 144(3)： 656-678.

[26] 王学滨, 马冰, 吕家庆. 实验室尺度典型断层系统破坏、前兆及粘滑过程数值模拟[J]. 地震地质, 2014, 36(3)： 845-861.

[27] SASANI M, YAZDANI M. Numerical simulation of earthquake mechanism based on stick-slip behavior of faults[J]. Proc Spie, 2010, 8670(4)： 126.

[28] 马晓静. 正断层发生地震的动力学过程数值模拟研究[D]. 北京：中国地震局地质研究所, 2012.

[39] 姜辉, 邓志辉, 高祥林, 等. 日本俯冲带地震发生过程的数值模拟研究[J]. 地球物理学报, 2013, 56(7)： 2303-2312.

[30] CRUZATIENZA V M, VIRIEUX J, OPERTO S. Dynamic Rupture Simulation of Bent Faults with a New Finite Difference Approach[C]// EGS-AGU-EUG Joint Assembly, 2003.

[31] 焦明若, 唐春安, 张国民, 等. 细观非均匀性对岩石破裂过程和微震序列类型影响的数值试验研究[J]. 地球物理学报, 2003, 46(5)： 659-666.

[32] XING H L, MORA P, MAKINOUCHI A. Finite Element Analysis of Fault Bend Influence onStick-Slip Instability along an Intra-Plate Fault[J]. Pure and Applied Geophysics, 2004, 161(9)： 2091-2102.

[33] 王学滨, 白雪元, 马冰. 断层系统中局部断层活动过程的数值分析方法——以Z字形断层为例[J]. 地球物理学进展, 2015(6)：2938-2944.

[34] 孙楠, 吴小平, 解朝娣, 等. 基于速率-状态依赖摩擦本构关系研究不同因素对断层黏滑运动的影响[J]. 云南大学学报自然科学版, 2014, 36(3)： 378-383.

[35] BARBOT S, LAPUSTA N, AVOUAC J P. Under the hood of the earthquake machine： toward predictive modeling of the seismic cycle[J]. Science, 2012, 336(6082)： 707-710.

[36] SHIBAZAKI B, OBARA K, MATSUZAWA T, et al. Modeling of slow slip events along the deep subduction zone in the Kii Peninsula and Tokai regions, southwest Japan[J]. Journal of Geophysical Research Atmospheres, 2012, 117(B6)： 6311.

[37] NODA H, LAPUSTA N. Stable creeping fault segments can become destructive as a result of dynamic weakening[J]. Nature, 2013, 493(7433)： 518-21.

[38] 邓志辉, 宋键, 孙君秀, 等. 数值模拟方法在地震预测研究中应用的初步探讨(Ⅰ)[J]. 地震地质, 2011, 33(3)： 670-683.

（责任编辑：刘格云）

A Review on Seismic Activity of Bending Fault

ZHANG Zeng-huan, MA Xiao-jing, WANG Shi

Hebei GEO University, Shijiazhuang, Hebei 050031

This paper analyses and summarizes the seism genic mechanism and the seismicity characteristics of bending fault, from these aspects: the bending fault seismicity characteristics, the rock physics experiments on the stick-slip motion of fault, the numerical simulation experiments on the Stick-slip motion of fault. The actual cases studies and observations show that the angle of bending fault and the bending point have important influence on the occurrence of earthquake, magnitude of earthquake and the fault rupture direction. Rock physics experiments have proved that some factors such as the material composition in fault zone, the friction coefficient of fault and the stress disturbance have a great influence on the characteristics of the fault stick-slip motion. Bending fault as a common form in nature, the study of the characteristics of stick-slip motion and its influencing factors would help us understand the mechanism of earthquakes and should be further strengthened in future research.

bending fault; seismic activity; stick-slip motion; numerical simulation

P548

A

1007-6875(2017)03-0013-06

日期：2017-03-08

10.13937/j.cnki.hbdzdxxb.2017.03.003

河北省研究生创新资助项目（1007703）。

张增换（1986—），女，河北石家庄人，硕士研究生，研究方向为区域地质构造与构造动力学。