林业科研中不同数据处理方法对方差分析结果的影响

马顺兴，苗作云，张少伟，鲁广伟

（1.河南投资集团有限公司，河南 郑州 450008；2.黄河科技学院，河南 郑州 450002；3.河南农业职业学院，河南 郑州 450003；4.原阳县农林畜牧局，河南 新乡 453500）

林业科研中不同数据处理方法对方差分析结果的影响

马顺兴1，苗作云2，张少伟3，鲁广伟4

（1.河南投资集团有限公司，河南 郑州 450008；2.黄河科技学院，河南 郑州 450002；3.河南农业职业学院，河南 郑州 450003；4.原阳县农林畜牧局，河南 新乡 453500）

为了研究不同的数据处理方法对方差分析结果的影响，该研究以省沽油6个种源的果实长度为例，研究了直接方差分析法、群体抽样法、分层抽样法、群体抽样求平均法及分层抽样取平均法5种方法分别对方差分析结果的影响。在方差分析过程中，增加样本量可以降低犯第1类错误的概率，但随着样本量的增加，可能得到具有统计学意义的显著差异而无实际利用价值。研究结果可以为林业科学研究的试验设计及数据处理提供参考。

方差分析；多重比较；试验设计

方差分析（Analysis of Variance，ANOVA）是进行差异比较的主要方法，在林业试验数据处理上应用广泛。林业外业试验误差较大，为了得到可靠的结论，一般以增加调查数据量的方法。研究以实际例子探讨几种数据处理方法对方差分析结果的影响，以期为科研工作者在试验设计及数据分析过程中提供参考。

1 数据来源

数据源自 2015年底调查三门峡地区省沽油（Staphylea bumalda DC.）6个种源的果实长度。

2 数据处理

用 Excel2007进行数据整理，采用 SPSS16.0进行方差分析和多重比较[1-4]。Duncan新复极差法比较数据间的差异检验，显著性水平设定为0.05。

2.1 数据整理方法

2.1.1 直接分组法

即完全随机抽样法，视种源内150例数据相互独立。

2.1.2 整群分类法

将每个种源的数据完全随机分为6组，即群体内有一定变异，群体随机。

2.1.3 分层分类法

将每组的数据进行排序，然后平均分为6组，类似于分层随机抽样，每层内数据变异较小，不同层次间变异较大。

2.1.4 整群分类求平均法

按整群分类法分为6组，以小组平均值为单位计算。

2.1.5 分层分类求平均法

按分层分类法分为6组，以小组平均值为单位计算。

2.2 方差分析模型及SPSS操作

2.2.1 单因素方差分析

其中μ表示不考虑不同种源时的平均果实长，Fi代表种源和总的平均水平相比时的差异，eij表示误差项。

2.2.2 嵌套数据方差分析

一般线性模型（General Linear Model，GLM）中的多因素方差模块（univarite）进行分析，选用的模型为 Yijk＝μ＋Fi＋Rj＋eijk的随机模型，其中Yijk是第i处理在第j区组中第k株的观测值；μ为试验群体平均数；Fi为种源效应；Rj为在种源内的群体（层次）效应；eijk为剩余项。

在 SPSS16.0中无法直接通过模块实现，因此具体操作为（以群体取样数据为例）：

Analyze—General Linear Model—univariate

因变量为果实长，在固定因素中选择种源，在随机因素中选择群体，因为在SPSS中无法直接通过模块直接实现嵌套试验设计的方差分析，因此需要通过paste语句实现，并将其改后运行。修改程序如下：

3 结果与分析

5种数据处理方法所得方差分析结果如表1所示，整群分类法和整群分类求平均法得到的F值和显著性概率相同，分层分类法和分层分类求平均法得到的F值和显著性概率相同。直接分组法和整群分类法（整群分类求平均法）得到不同种源间存在极显著差异，但直接分类法的显著性概率远远小于整群分类法（整群分类求平均法），而分层分类法（分层分类求平均法）得到不同种源间存在显著差异。即使是同一批数据，采用不同的方法处理，仍然可以得到不同的分析结果。

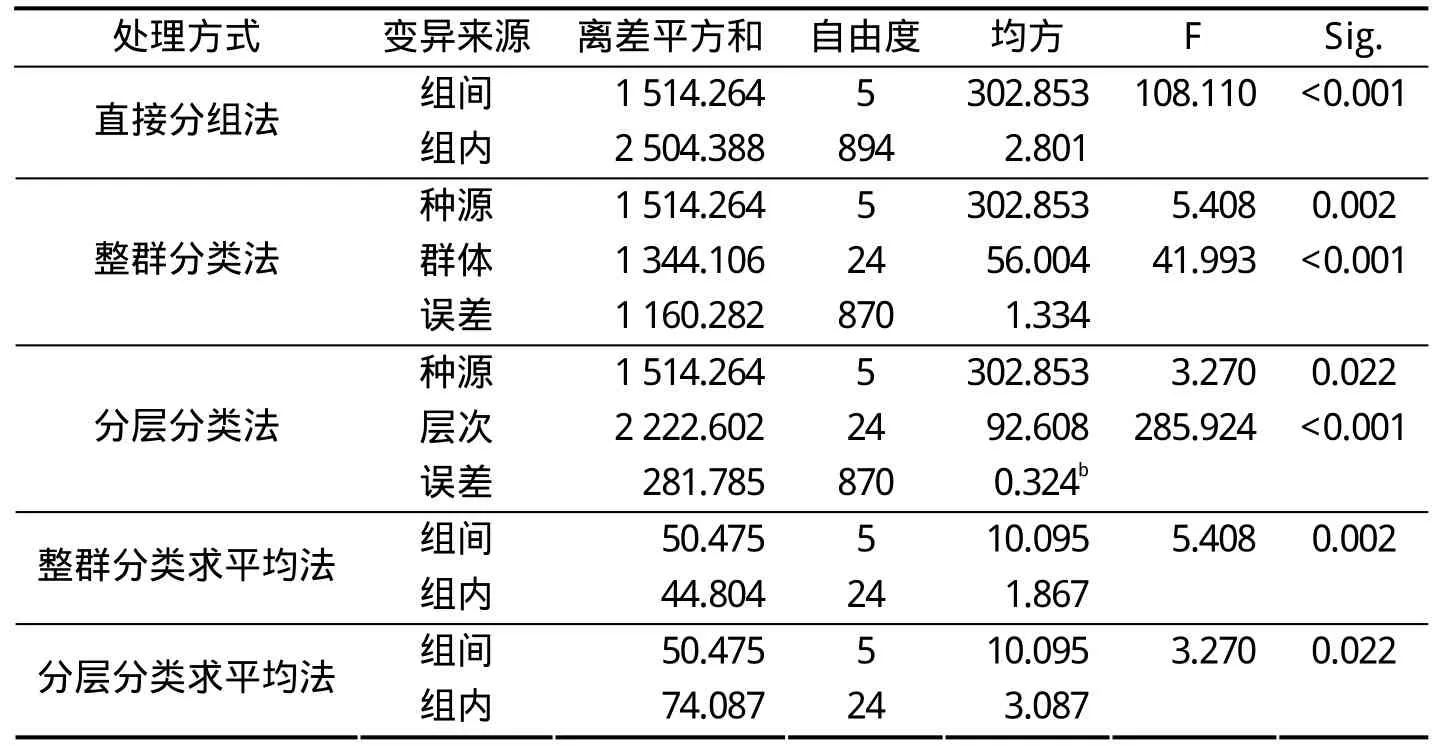
表1 方差分析

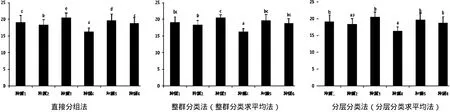
图1 不同处理方法所得的多重比较效果

不同处理方法所得到各个种源的多重比较结果 如图1所示，直接分组法得到多重比较，种源1和种源2平均值差值仅为0.67，但这两个种源的变异系数却分别是1.60～2.03，种源间的差异仅为种源内变异的 33.00%～41.88%，且这两个差值太小，虽有统计学上的差异，却无实际意义。分层分类（含分层分类求平均法）得到种源4和种源2间差异为2.03，但却无统计学上的显著性差异。整群分类法（含整群分类求平均法）得到的多重比较结果介于直接分组法和分层分类法（含整群分类求平均法）之间。

4 结论及建议

4.1 结论与讨论

本研究中得到同一批数据，按照不同的数据缩减方法或者方差分析方法，得到结果差异不同，其主要原因应归结于最终应用于方差分析的样本量的大小。查阅F检验的临界值表得到，在0.05的置信水平下，第1自由度为5，当第2自由度为24时的临界值为2.62，而当第2自由度为1 000时的临界值则为2.22，降低了15.27%，但自由度却升高了40.67倍，根据方差分析的计算公式，MS=SS/df，可得误差项的均方仅为原来的2.46%。

F值=MS组间/MS组内=（SS组间/df组间）/（SS组内/df组内），因此，在临界值变化幅度不大的情况下，F值却是以前的40.67倍。所以得出存在极显著或者显著差异的统计学结论，但这种结论是无实际意义的。

4.2 建议

在进行试验之前，应先进行初步调查，看整个研究群体的分布是否具有层次性，根据实际情况选择不同的抽样方法，为后期数据处理提供准确依据。

在调查取样时，数据量大小适当即可，过大的数据量会提高调查成本，同时会得到一些没有实际价值的统计结论。

当已经取得一批数据时，选用不同的数据缩减方法或者选用不同的方差分析模型来降低方差分析的自由度，从而得到更有实际价值的数据。

[1] 吴明隆. SPSS统计应用实务[M]. 北京：中国铁道出版社，2000.

[2] 张文彤，董伟. SPSS统计分析高级教程[M]. 北京：高等教育出版社，2004.

[3] 张文彤，董伟. SPSS统计分析高级教程[M]. 北京：高等教育出版社，2004.

[4] 郭志刚. 新编21世纪社会学系列教材：社会统计分析方法·SPSS软件应用[M]. 北京：中国人民大学出版社，2004.

（责任编辑：王文彬）

S757.2+4

A

1003-2630（2017）02-0026-03

2017-04-15

河南省科技攻关（162102110090）；郑州市2015年度科技发展计划（20150271）；中牟县技术研究与开发项目（zmkjj20160616）

马顺兴（1980-），男，河南新郑人，工程师，硕士，主要从事林业资源管理。通讯作者：张少伟（1981-），男，河南安阳人，讲师。