基于整群随机样本评估的简单随机抽样精度探讨

许学艳

（广西师范大学数学与统计学院 桂林 541004）

0 引言

随着我国经济的稳步增长，统计工作正在逐步向着与国际接轨的方向发展，抽样调查方法将在今后的统计工作中发挥越来越重要的作用，并将得到更为广泛的应用。目前在国内，尽管抽样调查方法已被广泛使用，但在采用随机抽样的过程中往往只注重于得到具体的抽样估计值，而不够重视如何给出抽样调查的精确度。

抽样调查中，当某个总体由若干个有着自然界限和区分的子群（或类别、层次）所组成，同时，不同子群之间差别不大，而每个子群内部的异质性比较大时，则特别适合采用整群抽样的方法。整群抽样是将总体划分为若干个群，然后以群为抽取单元，从总体中随机抽取一部分群，对入选群内所有单元进行调查的一种抽样方法。国内外专家学者对于简单随机抽样的简单估计和比估计以及整群抽样的估计精度做了许多具体的研究。本文基于整群随机抽样，研究如何用一个整群样本来对同样样本量下简单随机抽样作简单估计和比估计，从而降低成本、提高效率和精度。

1 基于简单随机抽样下的简单估计和比估计

简单随机抽样又称单纯随机抽样，指的是从总体个单元中，逐个不放回地抽取单元，每次抽到尚未入样的任何一个单元的概率都相等，直到抽足个单元为止。

1.1 简单估计

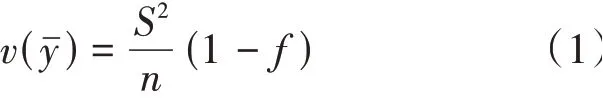
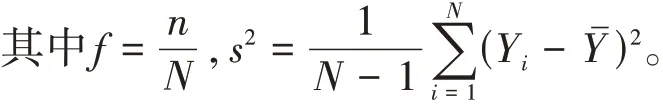
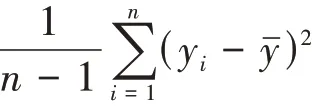
1.2 比估计

在抽样调查中会用到比率估计量的情况有两类，一类是所需估计的目标值是两个指标总数（或均值）的比值，另一类则是所需估计的目标值是某指标的总数（或均值），但有另一个与密切相关的指标可作为辅助变量。利用辅助变量的信息可改进估计的精度。辅助变量的特点可归纳为以下几条：必须与主要变量高度相关；与主要变量之间的相关关系整体上相当稳定；辅助变量的总体总值必须是已知的，或是容易获得的；辅助变量的信息质量更好，或信息更容易取得即调查成本更低。实际问题中，X常是Y的前期资料。

总体均值ˉ和总值Y的比估计量定义为

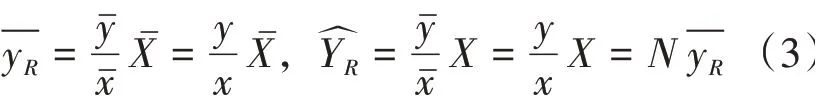
比估计是有偏估计，但样本量增大时，偏倚趋于零。此时均方误差与方差近似相等。

当较大时，对于简单随机抽样有

当足够大时：

而对于简单估计ˉ，有

2 基于整群随机样本下的群规模相等估计以及效应分析

为了提高样本效率，减少样本量，实际工作中检查先对总体进行分群，再进行等概率的整群抽样。整群抽样的特点为：抽样框编制得以简化，实施调查便利、节省费用。

2.1 群规模相等时的估计

采用整群抽样，若群的抽取是简单随机的，且群规模相等，皆等于，则对总体均值˭的估计为

2.2 整群抽样效应分析

如果该总体被等分为N个规模均为M的群，定义ρ为群内相关系数，描述同一群内成对个体单元之间的相关程度，表达式为

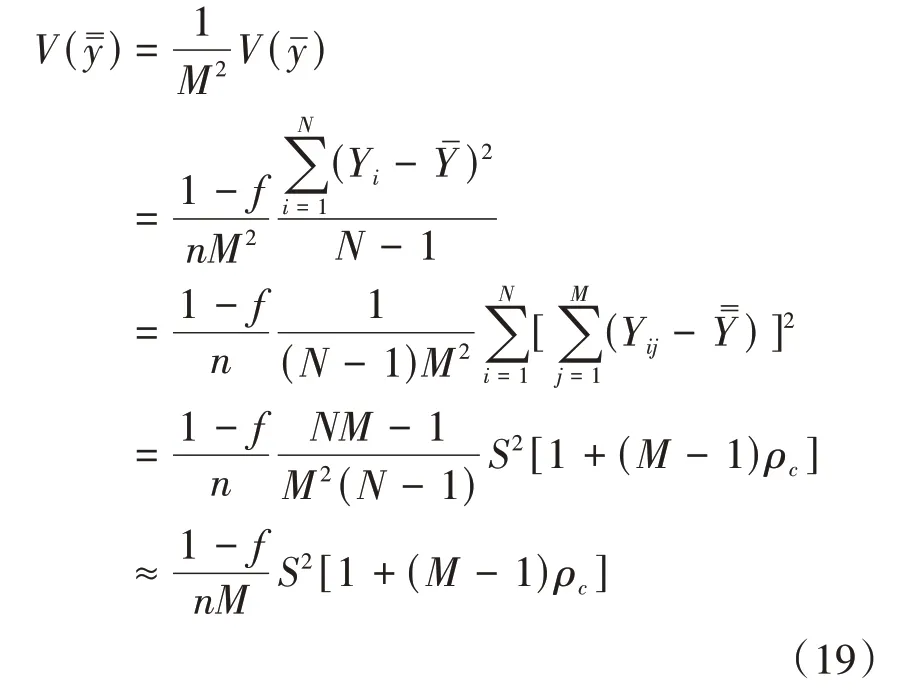
这说明，相同样本容量下整群抽样方差约为简单随机抽样方差的1+（-1）ρ倍。也就是说，为了得到相同的估计精度，整群抽样的样本容量是简单随机抽样样本容量的1+（-1）ρ倍。

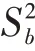
式中，

3 群规模不等时的估计

3.1 简单估计

在实际的社会调查中，群规模不等的情况更为常见。从个群中等概率抽取个群的整群样本，如果各群规模M不等，那么运用群规模相等时的估计方法的估计量是有偏的，尤其是当各群规模M差异很大，且-y与M存在较高相关时，估计量的偏差会很大。

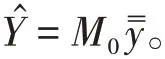
上述估计量的方差为

它的无偏估计为

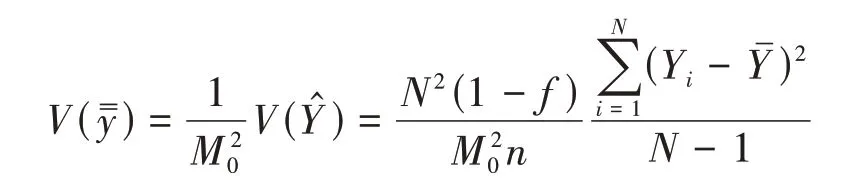
3.2 比估计

我们通常预期y与M是相关的，以M为辅助变量，总体均值的比率估计量为

当样本群数很大时，总体总值的比率估计量为

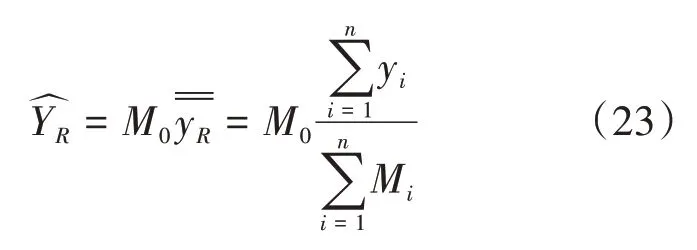
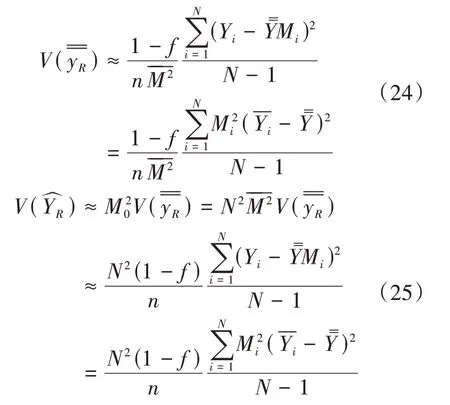
4 实例分析

为调查某地区农作物的总产量，以该地区的村庄数、种植面积为辅助变量，利用无偏估计量和比率估计量进行估计。

4.1 无偏估计

尽管此种方法可获得无偏估计量，但其估计方差与y之间的差异有关，它适用于y之间几乎没有差异的整群抽样。

4.2 以群规模为辅助变量的比率估计

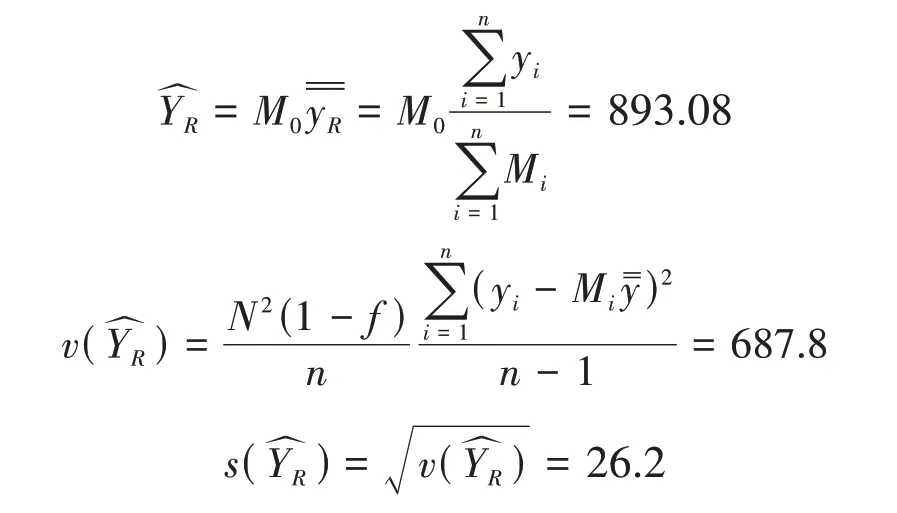
4.3 以种植面积为辅助变量的比率估计

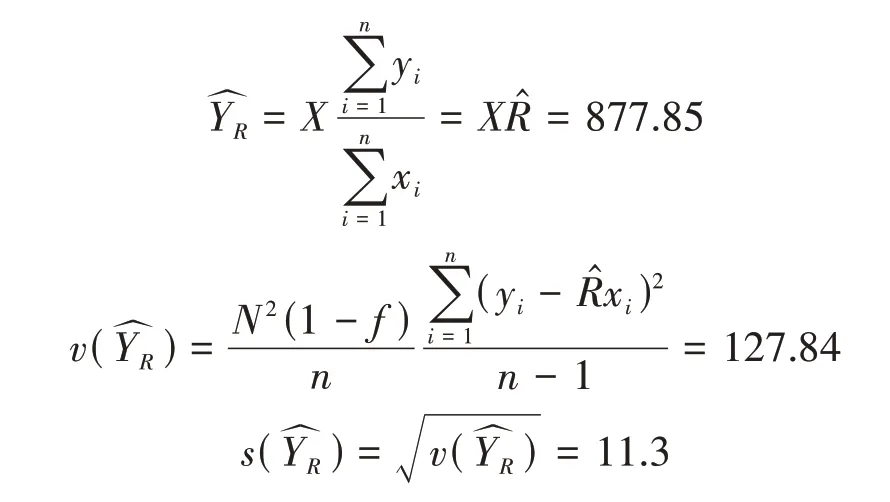
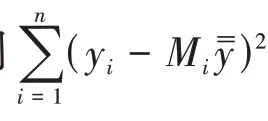
5 结语

本文给出了一种基于整群随机样本，同样样本量的简单随机抽样精度的评估公式，并通过具体实例与简单随机抽样的简单估计，以不同的群规模为辅助变量的比率估计在精度上做了比较。结果表明基于不等整群抽样的比率估计量的精度更高。