一节“内容简单”课的教学思考

安徽省怀远第三中学 (邮编：233400)

一节“内容简单”课的教学思考

安徽省怀远第三中学宋在馥(邮编：233400)

学校举行青年教师汇报课活动，委托笔者出题，我指定的是北师大版数学必修(1)第一章《集合》的最后一节《全集与补集》， 提前2个小时供题，无材料备课，我也作为评委参加听评课.

有位年青教师教材很熟，简单地看看课本，很快地完成教学设计.开始上课，他先是从生活中举一些例子，设置全集与补集的情境，又别出心裁地拿出一块方纸，说是全集U，从中撕下一块说是集合A，剩下的部分即为补集UA，生动地说明了全集U的子集A的补集的定义，以及集合表示UA={x|x∈U且x∉A}，并轻松地得出结论A∪(UA)=U.

教材中的概念部分就是这些，下面是两道例题.

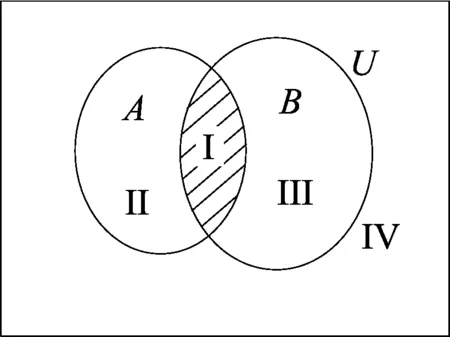
例3试用集合A、B的交集、并集、补集分别表示图1中I、II、III、IV四个部分所表示的集合，答案是：

Ⅰ部分：A∩B；

Ⅱ部分：A∩(UB)；

Ⅲ部分：B∩(UA)；

Ⅳ部分：U(A∪B)或(UB)∩(UA)．

例4设全集为R，A={x|x<5}，B={x|x>3}．求：

(1)A∩B； (2)A∪B；

老师采用取学生自己求解，合作交流，成果展示，集体评议的方式，很快地把这两个例题干脆利索地解决了，同时还让学生探究发现了两组结论：

然后学生们总结，老师点评，最后做了几道练习作为学习效果的检测.从对学生的检测结果上看，学生学得比较好，还剩有时间.老师又机智地安排了几道题让学生练习，要求同位之间相互检查，最后分小组汇报结果.所有的程序进行完毕，下课铃声响起，同时响起的还有热烈的掌声，鼓掌的有学生更有老师.

随后是评课，老师们较为一致的评价是：这节课内容非常简单，不利于老师发挥，不过能上成这种效果，已经难能可贵了.从学生的检测结果与课堂的学习氛围来看，是一节非常成功的课，不要说是青年教师，就是资深教师也不过如此.大家讲完后，目光齐聚向我这个出题人，我便谈了如下的看法，实际上也是对如何用教材教的思考.

指定《全集·补集》作为课题，有点出乎预料，以往大致都是函数的单调性、奇偶性、余弦定理、正弦定理、三角函数图象、等差等比数列、椭圆及其标准方程等作为课题.而这节从教材上看确实简单，两个概念，内容叙述不足300字.两个例题，也较容易解答，确实是大家平时所讲的“没有什么好讲”的课.这节课如大家所评，是一节非常成功的课.我们是否就到此为止，能不能再有深入的思考？如果还想提高课的质量，提升课的品位，就让我们回顾一下《普通高中数学课程标准》的第二部分“课程目标”，具体目标有六个部分，其中第六部分：“具有一定的数学视野，逐步认识数学的科学价值，应用价值和文化价值.形成批判性的思维习惯，崇尚数学的理性精神，体会数学的美学意义，从而进一步树立辩证唯物主义和历史唯物主义世界观.”

我们的每一节课，应该尽可能多的达成所列的目标.这节课所完成的仅仅是基本目标，或说初级目标，底线目标.现在我们一起再来分析一下教材，看看还可以挖掘出哪些宝藏：

1 关于定义所得结论的哲学意义：

由补集定义不难得出：A∪(UA)=U，

A∩(UA)=∅

①

②

对结论②引发思考：我们以往知识中有类似的结论吗？这就进入了学生的最近发展区.学生容易想到，相反数的相反数是其本身，倒数的倒数是其本身，这也体现了辩论法的三大规律之一，“否定之否定”规律.由此启发学生认识到A∩(UA)=∅是“对立”，A∪(UA)=U是“统一”，体现了辩证法的“对立统一”规律.这既有了哲学思辨，又有了文化价值，还体会到审美意义.

同时，数学中的反证法和计算中的“正难则反”技巧，都有补集内容作理论基础.

2 关于例3的结论在分类方面的应用价值

对于例3可以得到这样的结论，设A、B是全集U的两个子集，那么可以将全集分成不重不漏的四个部分：A∩B，A∩(UB)，B∩(UA)，(UA)∩(UB).

这个结论有很高的应用价值，有了全集U不重不漏的四块分割，确实对数学问题的分类讨论，有一种潜在的指导意义.比如：

某小组有6个人，选派3名去参加青年志愿者活动，要求甲乙不同时去，问有多少种选派方法.

此时这个结论的应用价值就体现出来了，先将选派方法分类：甲去且乙去，甲去且乙不去，乙去且甲不去，甲不去且乙不去.恰好对应上述全集U的四个部分.而甲乙不同时去恰好包含后三类，可采用“正繁则反”的方法计算.

有些虽然不是严格意义上的与此对应，但从分类的思维上却是相似的，有借鉴和启发作用.

比如，做题中常涉及到的不等式成立问题，有以下结论f(x)、g(x)均存在最值：

∀x1∈M，∀x2∈N，使f(x1)≤g(x2)成立⟺f(x)max≤g(x)min；

∀x1∈M，∃x2∈N，使f(x1)≥g(x2)成立⟺f(x)min≥g(x)min；

∃x1∈M，∀x2∈N，使f(x1)≥g(x2)成立⟺f(x)min≥g(x2)max；

∃x1∈M，∃x2∈N，使f(x1)≤g(x2)成立⟺f(x)max≤g(x2)min.

如对函数按奇偶性分类，便有奇函数和偶函数，既是奇函数又是偶函数，既非奇函数也非偶函数四类.

对两个命题从充分条件与必要条件上厘清关系，可以分成“充分不必要条件，必要不充分条件，充分且必要条件，既不充分也不必要条件”四种.如要做|x|+|y|=1的图象，可按“x≥0且y≥0，x≥0且y<0，x<0且y≥0，x<0且y<0”等四种情况讨论.

再如企业对人才的分类：以“德”与“才”为标准可以将员工分成四类：有德有才的，有德无才的，有才无德的，无才无德的.这分类以后，就可以排等次，选择使用.

我们平时常讲，要培养学生的数学意识，能在全集U不重不漏的四块分割启发下，迅速准确分类，就是数学意识增强的表现.

3 关于例4的两结论的理性精神

观察计算结果可以发现这样的结论：

这个结论是对计算结果的一种猜想，课本上的习题，要求用Venn图来分析说明.无论是对计算结果的猜想，还是用Venn图观察，都算不上严格的证明.实际上完全可以应用交集，并集与补集的定义来证明.

证明∀x∈U(A∩B)，则x∉(A∩B)，必有x∉A或x∉B，

那么x∈UA或x∈UB故x∈(UA)∪(UB).

所以U(A∩B)⊆(UA)∪(UB).

对∀x∈(UA)∪(UB)，则x∈(UA)或x∈(UB)故x∉A或x∉B.

从而x∉(A∩B)，故x∉∪(A∩B).

故(UA)∪(UB)⊆U(A∩B)，

同理可证：

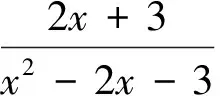
学生在解此题时，答案不外乎两种：{x|x≠-1或x≠3}或{x|x≠-1且x≠3}，

我们多次纠正，总还会出答案是{x|x≠-1或x≠3}的错误，这是受了解方程x2-2x-3=0，x1≠-1或x=3的负迁移.如果不从根本上讲清，以后还会再犯这样错.运用上述公式，恰好可以清晰地说明错误的根源.记A={x|x≠-1}，B={x|x=3}，M={x|x2-2x-3=0}=A∪B，{x|x2-2x-3≠0}=RM=R(A∪B)=(RA)∩(RB)={x|x≠-1}∩{x|x≠3}={x|x≠-1且x≠3}，联词是“或”还是“且”便真相大白，如此才能做到真正地理解，做出的判断才是理性的.

4 关于备课和上课的思考与建议

以上是对这节课的一些思考，当然并不是要求教师在课堂上把这些内容当做教学任务来完成，只想让大家感到，不能仅仅从教材的形式上去判断内容的简单与复杂，浅显与深奥.教材仅仅是一个范本，需要我们去“用教材教”而不是“教教材”，至少我们备课时要想到这些或更多.课堂教学中，尽可能地去启发学生，探及到这些，以期有更多更好的生成.因此在备课中，应该熟悉新课程标准中的十大基本理念和六大课程目标，于是有以下建议：

(1)确定合理的教学目标.这一点最受重视而常常又被忽视，因为现在有了三维目标的要求，因此教案上必有这“知识与技能”“过程与方法”和“情感态度与价值观”，却常常又是大而空.课堂上看似有目标，实际是信马由僵.应根据课标中的六大课程目标，以及学生核心素养指标，结合学生的最近发展区，确立“具体、明晰、可实现”的目标，这个目标既能指导课堂教学，又利于检测达成度.

(2)充分地利用教材.教材是一个柠檬，需要老师把它做成柠檬水.过去对教材的分析，只在数形结合、转化、分类讨论及函数与方程的思想及方法层面.现在提倡的是“具有一定的数学视野，认识数学的科学价值和人文价值，崇尚数学的理性精神，形成审慎的思维习惯，体会数学的美学意义.”要求将教材的效益最大化，因此要在课程理念的指导下，根据课程目标，去充分地挖掘教材.

(3)机智地调控课堂.课堂是可预设但不可预知的.通过过程，完成“知识与方法”的教与学，进一步地去达成“情感态度与价值观”层面的目标，这是预设，当然可能会出现“意外”.比如学生在基础学习上出现障碍，那我们的目标可以削减，内容可以“裁军”.比如证明结论U(A∪B)=(UA)∩(UB)，并不是预设的内容，而课堂上学生对此深感兴趣，那么我们不妨调整内容，与学生一块做一次“探索与发现”.比如，学生受例3中的U的子集A与B将U分成不重不漏的四个部分的启发，大家在寻找例子上乐此不疲，积极性空前高涨，我们可以放弃其他内容，让学生做一次“知识大搜寻”.课堂调控应坚持一个原则，凡是有利于培养学生能力与意识的生成都是有价值的.

海尔集团总裁张瑞敏有言：简单的事情做好了就是不简单.

1 普通高中课程标准实验教材《数学》(必修1)[M].北京：北京师范大学出版社

2 中华人民共和国教育部制订.普通高中数学课程标准[M].北京：人民教育出版社

2017-03-26)