复杂网络上具出生和死亡的一类分数阶SIR模型的全局渐近稳定性

魏晓丹

(1. 大连民族大学计算机科学与工程学院，辽宁 大连 116600；2. 吉林大学计算机科学与技术学院，吉林 长春 130012)

复杂网络上具出生和死亡的一类分数阶SIR模型的全局渐近稳定性

魏晓丹1,2

(1. 大连民族大学计算机科学与工程学院，辽宁 大连 116600；2. 吉林大学计算机科学与技术学院，吉林 长春 130012)

研究了复杂网络上具出生和死亡的一类分数阶SIR模型地方病平衡解的全局渐近稳定性。在某些额外的条件下，这个问题已被讨论。通过构造一个Lyapunov函数，在没有任何额外的条件下，证明了该模型地方病平衡解的全局渐近稳定性。这个结果改进了已有文献中的一个结果。

复杂网络；分数阶微分方程；全局渐进稳定性；Lyapunov函数方法

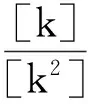
是度值为k的节点的分布函数，n为所有节点的最大度数，并指出：如果传播率超过这个临界值，那么疾病将会持续传播，并转化为地方病。对这一结果的数学证明于2008年由Wang等[3]给出。自Pastor-Storras和Vespignani的研究工作以来，复杂网络上流行病模型的传播动力学得到了广泛研究，这其中的一个重要课题便是复杂网络上微分方程模型的稳定性分析，参见文献[4-13]。

然而，目前所见到的复杂网络模型大多都是用整数阶微分方程模型来描述的，其局限是不能准确地描述记忆特征、历史依赖性等，而分数阶微分方程模型能很好地弥补这些缺陷。另一方面，现有的大多数网络中研究传播动力学是没有考虑出生和死亡的静态网络，但对于这类网络传染病模型，由于出生会导致网络的增长，而死亡会导致网络的衰减，因而会影响网络的结构，使得模型的稳定性分析更为困难。 在文献[14]中, 作者考虑了上述两个方面，并提出了如下复杂网络上的分数阶微分方程模型：

k=1,2,…,n

(1)

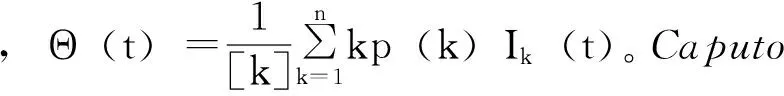
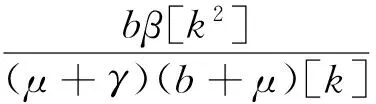
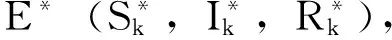
k=1,2,…,n

而Θ*是如下方程的唯一正解：

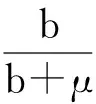
定理1 设R0>1，那么系统(1)的地方病平衡解是全局渐近稳定的。

1 若干引理

为证明定理1，不加证明地引用如下引理。

引理1[16]设x(t)∈R是一个连续可导函数，则

Dαx2(t)≤2x(t)Dαx(t)

引理2[14]设x(t)∈R+=(0,+∞)是一个连续可导函数，则

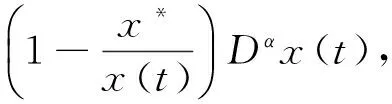
2 定理的证明

定理1的证明 设 (Sk,Ik,Rk)为问题 (1) 的一个解。令V=V1+V2+a1V3+a2V4, 其中

Nk=Sk+Ik+Rk,

并且a1,a2为正常数。接下来，计算函数Vi(i=1,2,3,4)的导数。首先，由引理1及Sk满足的方程得

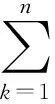
(2)

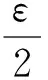
将其代入式(2)得

(3)

利用引理2及Θ满足的方程：

得

(4)

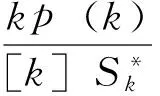
DαV1(t)+DαV2(t)≤

(5)

利用引理1及Nk满足的方程：

DαNk=b-(b+μ)Nk

得

(6)

用引理1及Rk满足的方程得

(7)

由Young不等式得

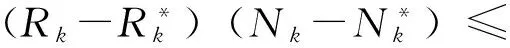
将这两不等式代入式(7)得

(8)

联合式(5)，式(6)及式(8)，并取

有

DαV=DαV1+DαV2+a1DαV3+a2DαV4≤

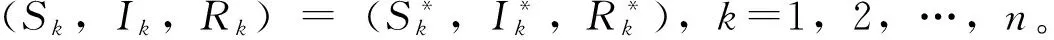
[1]PASTOR-SATORRASR,VESPIGNANIA.Epidemicspreadinginscale-freenetworks[J].PhysicalReviewLetter, 2001, 86(14): 3200-3203.

[2]PASTOR-SATORRASR,VESPIGNANIA.Epidemicdynamicsinfinitesizescale-freenetworks[J].PhysicalReviewE, 2002, 65(3): 035108(R).

[3]WANGL,DAIGZ.Globalstabilityofvirusspreadingincomplexheterogeneousnewworks[J].SIAMJournalonAppliedMathematics, 2008, 68(5): 1495-1502.

[4]LIUJZ,TANGYF,YANGZR.Thespreadingofdiseasewithbirthanddeathnetworks[J].JournalofStatisticMechanics, 2004, 2004:P08008.

[5]YANGM,CHENGR,FUXC.AmodifiedSISmodelwithaninfectivemediumoncomplexnetworksanditsglobalstability[J].PhysicaA, 2011, 390: 2408-2413.

[6]LIUJL,ZHANGTL.EpidemicspreadingofanSEIRSmodelinscale-freenetworks[J].CommunicationinNonlinearScienceNumericalSimulation, 2011, 16(8): 3375-3384.

[7]ZHANGJP,JINZ.Epidemicspreadingoncomplexnetworkswithcommunitystructure[J].AppliedMathematicsandComputation, 2012, 219(6): 2829-2838.

[8]ZHUGH,FUXC,CHENGR.Globalattractivityofanetwork-basedepidemicSISmodelwithnonlinearinfectivity[J].CommunicationinNonlinearScienceNumericalSimulation, 2012, 17(6): 2588-2594.

[9]FERREIRAS,CASTELLANOC,PASTOR-SATORRASR.Epidemicthresholdsofthesusceptible-infected-susceptiblemodelonnetworks:acomparisonofnumericalandtheoreticalresults[J].PhysicalReviewE, 2012, 86(4): 041125.

[10]LIT,WANGYM,GUANZH.SpreadingdynamicsofaSIQRSepidemicmodelonscale-freenetworks[J].CommunicationinNonlinearScienceNumericalSimulation, 2014, 19(3): 686-692.

[12]LIC.Dynamicsofanetwork-basedSISepidemicmodelwithnonmonotoneincidencerate[J].PhysicaA, 2015, 427: 234-243.

[13]WEIXD,LIULJ,ZHOUWS.Globalstabilityandattractivityofanetwork-basedSISepidemicmodelwithnonmonotoneincidencerate[J].PhysicaA, 2017, 469: 789-798.

[14]HUOJJ,ZHAOHY.DynamicalanalysisofafractionalSIRmodelwithbirthanddeathonheterogeneouscomplexnetworks[J].PhysicaA, 2016, 448: 41-56.

[15] 丁金凤, 金世欣, 张毅. 基于Caputo导数下的含时滞的Hamilton系统的分数阶Noether理论[J]. 中山大学学报(自然科学版), 2016, 55(6): 79-85.DINGJF,JINSX,ZHANGY.FractionalNoethertheoremsforHamiltonsystemwithtimedelaybasedonCaputodervitaves[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2016, 55(6): 79-85.

[16]AGUILA-CAMACHON,DUARTE-MERMOUDMA,GALLEGOSJA.Lyapunovfunctionsforfractionalordersystems[J].CommunicationsinNonlinearScienceandNumericalSimulation, 2014, 19(9): 2951-2957.

GlobalstabilityofafractionalorderSIRmodelwithbirthanddeathoncomplexnetworks

WEIXiaodan1,2

(1.SchoolofComputerScienceandEngineering,DalianMinzuUniversity,Dalian116600,China;2.SchoolofComputerScienceandTechnology,JilinUniversity,Changchun130012,China)

The global stability of the endemic equilibrium of a fractional order SIR model with birth and death on complex networks is studied. Under some additional conditions, the problem is discussed. It is proved by constructing a Lyapunov function that without any additional condition, the endemic equilibrium is globally asymptotically stable. The result improves previous work.

complex networks; fractional order differential equation; global stability; Lyapunov function mehtod

10.13471/j.cnki.acta.snus.2017.04.004

2017-04-06 基金项目：国家自然科学基金(11571062)；中央高校基本科研业务费(DC201502030407)

魏晓丹(1978年生)，女；研究方向：复杂网络；E-mail:weixiaodancat@126.com

O

A

0529-6579(2017)04-0020-04