带线性与非线性延迟项的Volterra积分方程研究

郑伟珊

（韩山师范学院数学与统计学院，广东潮州521041）

带线性与非线性延迟项的Volterra积分方程研究

郑伟珊

（韩山师范学院数学与统计学院，广东潮州521041）

主要研究了一类带线性延迟项与非线性延迟项Volterra型积分方程的收敛情况．首先通过线性变换，将原先定义在[0,T]区间上的带线性与非线性延迟项的Volterra型积分方程转换成定义在固定区间[-1,1]上的方程，然后利用Gauss积分公式求得近似解，进而再利用Chebyshev谱配置方法分析该方程的收敛性，最终借助格朗沃不等式及相关引理分析获得方程在L∞和L2ωC范数意义下呈现指数收敛的结论，最后给出数值例子，算出误差估计并绘图展示，藉此验证理论证明的结论.

Chebyshev谱配置方法；线性延迟项；非线性延迟项；Volterra型积分方程；误差分析

1 介绍

主要研究带线性与非线性延迟项的Volterra积分方程，其形式如下

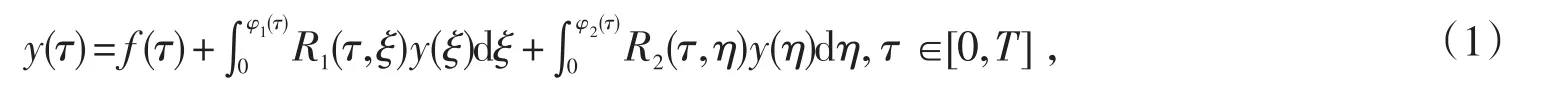
这里y(τ)是定义在[0,T](T＜+∞)上的未知函数，φ1(τ)=qτ，φ2(τ)=qτ2，q是常数且0＜q＜1．f(τ),R1(τ,ξ),R2(τ,η)是已知函数，其中f(τ)∈Cm[0,T]，R1(τ,ξ)∈Cm(Ω1)，R2(τ,η)∈Cm(Ω2)，m≥1,

Volterra型方程作为数学模型出现在许多领域中，包括机械物理问题、天体运动问题、生物种群原始状态变化问题等．带延迟项与非延迟项的Volterra型积分方程作为Volterra型方程的一个分支，它通常出现在具有时滞问题的刻画上，比如股票的震荡、生物种群繁衍等．关于Volterra型方程的研究受到较为广泛的关注，香港中文大学汤涛[1]教授用勒让德谱配置方法研究了Volterra方程的收敛性问题，随后华南师范大学陈艳萍教授与汤涛教授共同研究了带弱奇异核的Volterra型积分方程[2]，采用雅克比谱配置方法并获得收敛性结论．此外研究Volterra型积分方程还有噶辽金方法[3-4]、契比雪夫谱方法[5]等等．本文在之前工作[6]基础上使用契比雪夫谱方法研究带线性延迟项与非线性延迟项的Volterra型积分方程．

2 契比雪夫谱方法

在介绍契比雪夫谱方法之前，先介绍两类点：首先对于一个给定的自然数N，用{θk}Nk=0表示N+1勒让德高斯点[7]，用表示勒让德权，则相应的勒让德高斯积分法则为

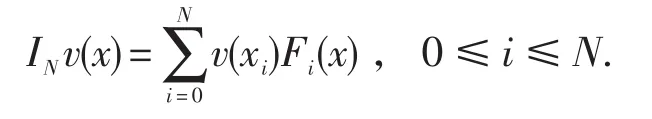
这里Fi(x)是以为插值基点的第i个插值基函数．

通过以下变量变换把方程（1）转化为定义在[-1,1]上

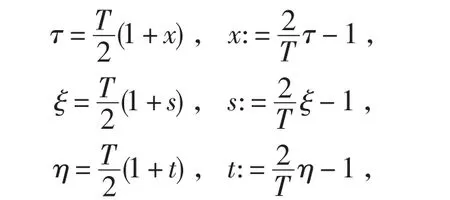
倘若令

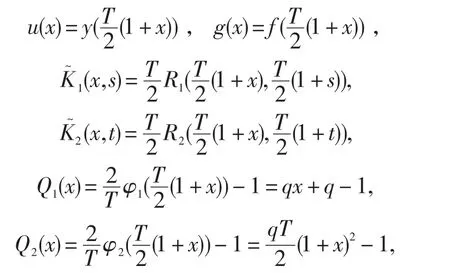
则方程（1）相应又可以转换为如下形式

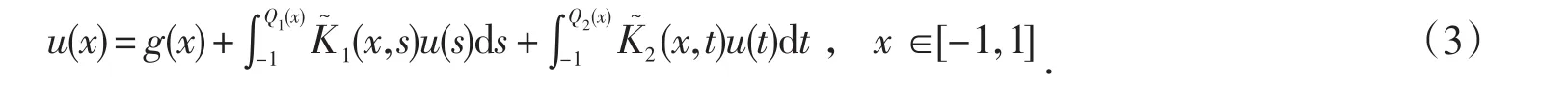
再通过如下变换将（3）中两个变上限[-1,Q1(x)],[-1,Q2(x)]积分转换为固定区间[-1,1]

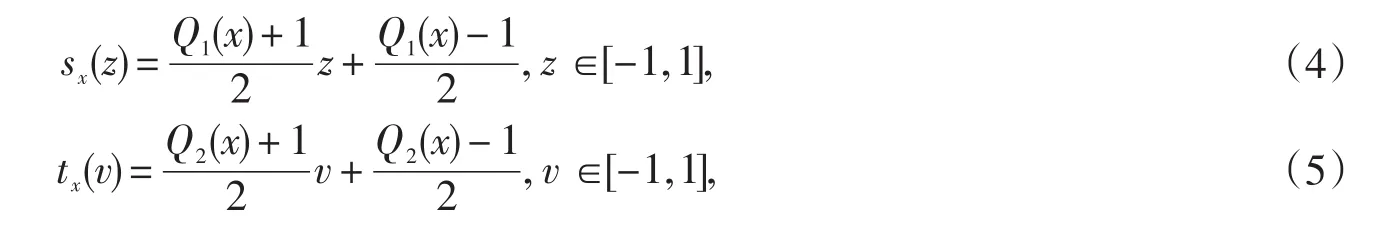
则方程（3）化为

显然以上方程在点xi恒成立，故有

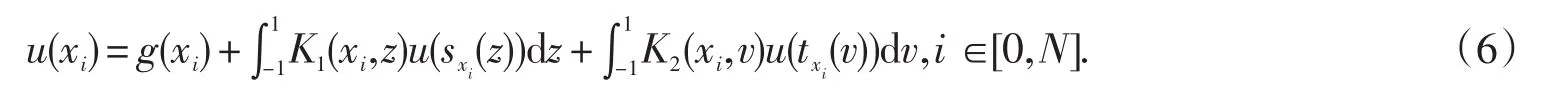
使用N+1点的勒让德积分法则（2）(相应的权为ωk)，可以得到如下近似式

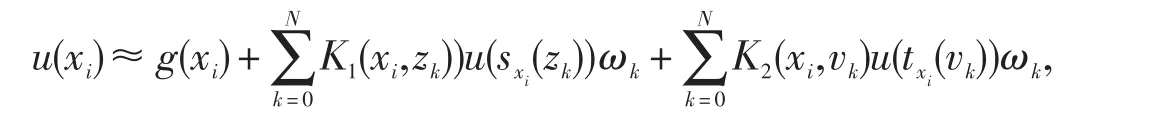
这里i=0,1,2,...,N，zk=vk是N+1个勒让德高斯点[7]．，显然uN(x)∈PN．契比雪夫谱配置方法就是寻求uN(x)使之满足如下方程:i=0,1,2,...,N，

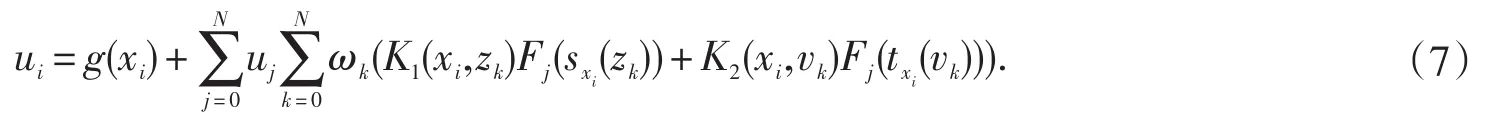
3 相关空间及引理介绍

本节中介绍一些引理，这些引理在接下来的证明中要用到，而为了更方便地介绍引理内容，先引入如下几个空间．

令ωα,β(x)=(1-x)α(1+x)β普通意义下的权函数，这里α,β＞-1，记为如下定义的空间是可测的，且，其模为,相应的内积为

对于非负整数m，定义空间

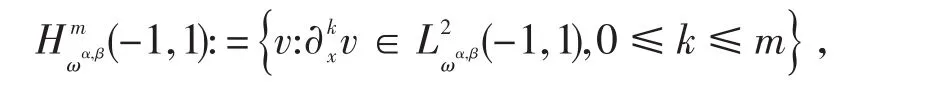
相应的模和半模分别为

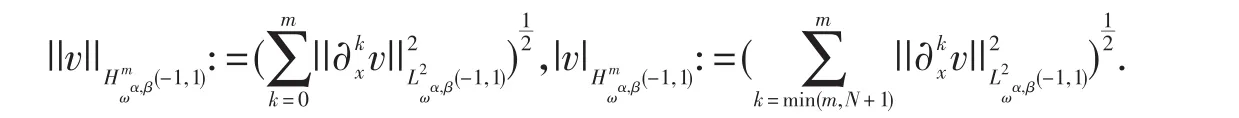
特别地，当α=β=0，用Hm(-1,1)表示；当，用ωc表示下面介绍引理

引理3.1[7-8]假设，m≥1，INu是以N+1契比雪夫高斯点为插值基点的插值算子，即，则有

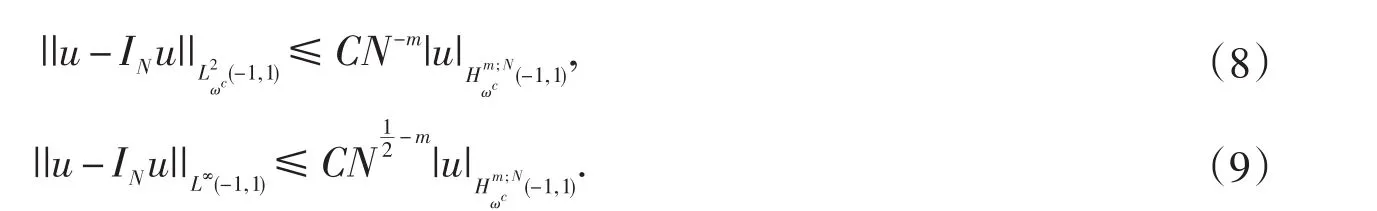
引理3.2[7-8]假设，则存在一个不依赖于N的常数C使得

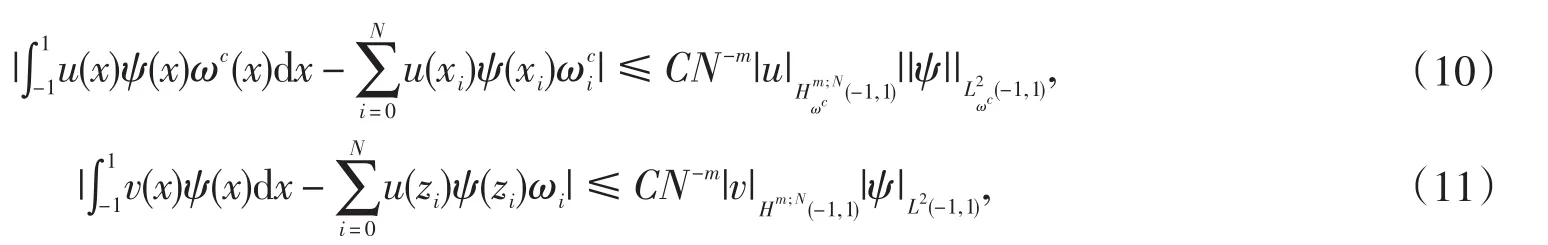
这里xi是N+1契比雪夫高斯点，相应的权为，而zi是N+1勒让德点，相应的权为ωi，i=0,1,2,3...,N.

引理3.3[2，9]令Fi(x)是以N+1个契比雪夫高斯点为插值基点的第i个拉格朗日插值基函数，

则有

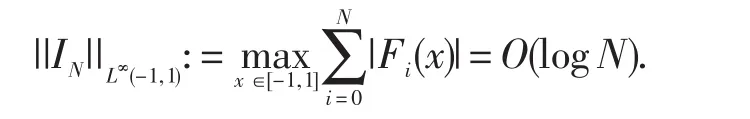
引理3.4[3，10]（Gronwall不等式）假设u(x)是一个定义在[-1，1]上的非负局部可积函数满足

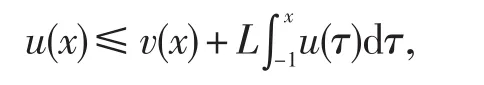
这里L≥0是一个常数，v(x)也是一个可积函数，则存在一个常数C使得并且

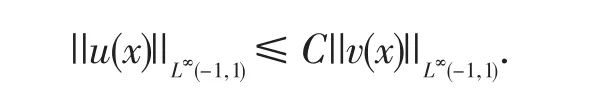
引理3.5假设0≤M1,M2＜+∞，如果一个非负可积函数e(x)满足

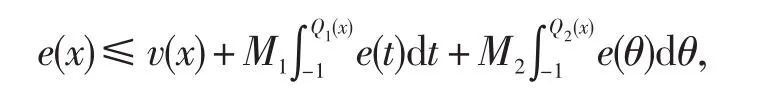
这里v(x)也是一个非负可积函数，则

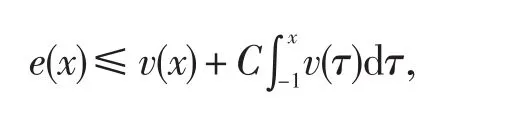
并且

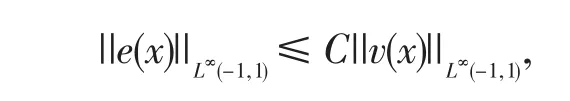
这里C是一个常数．

证明因为

故有

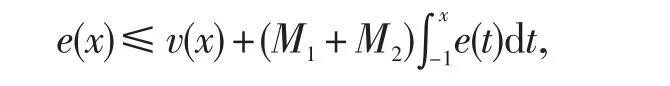
依据引理3.4可获证引理结论

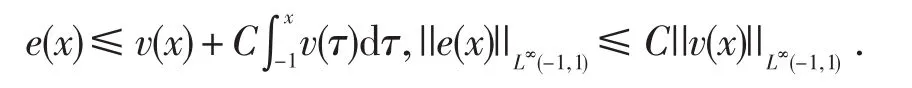
引理3.6[11]对于一切可测函数f≥0，如下广义Hardy不等式成立

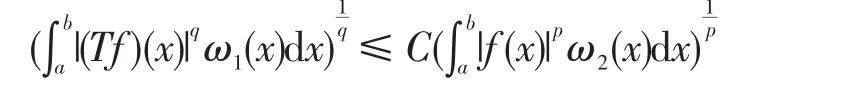
当且仅当

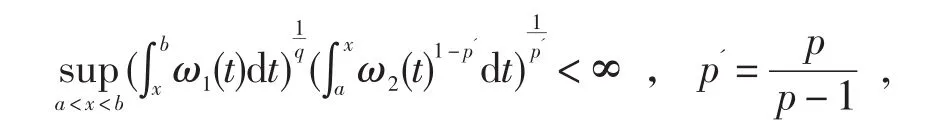
引理3.7[2，12]对一切有界函数v(x)，存在一个不依赖于v的常数C使得

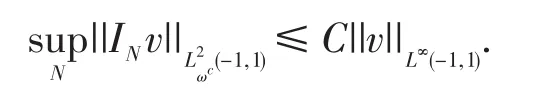
4 收敛性分析

使用契比雪夫谱配置方法对方程（3）进行收敛性分析，目标是获得方程在L∞以及空间中误差均呈指数收敛．

4.1 L∞(-1,1)空间中的收敛性分析

定理4.1设u(x)是方程（3）的精确解，而uN(x)是通过契比雪夫谱配置方法所获得的近似解，则当N足够大时，有

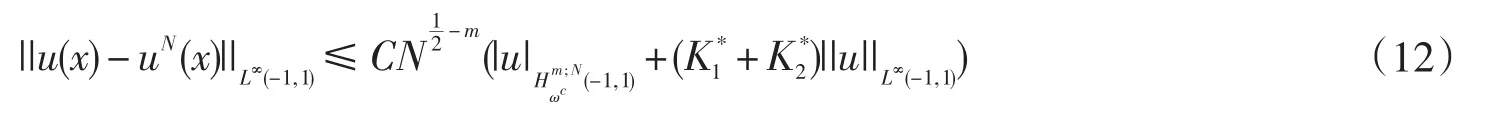
这里

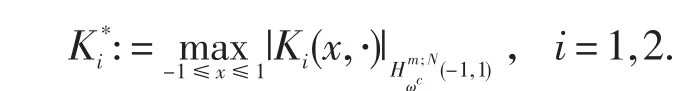
证明方程（6）减去（7）得

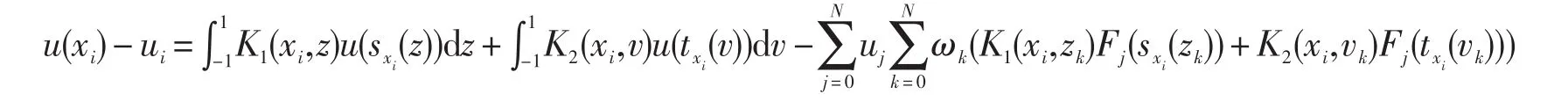
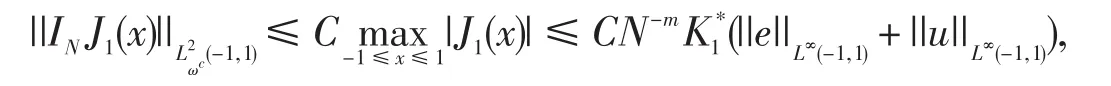
利用定理4.1的结论，令m=1有

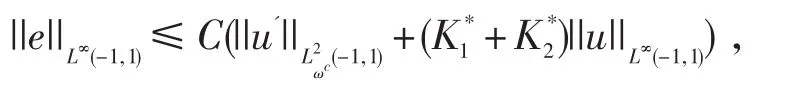
故得：

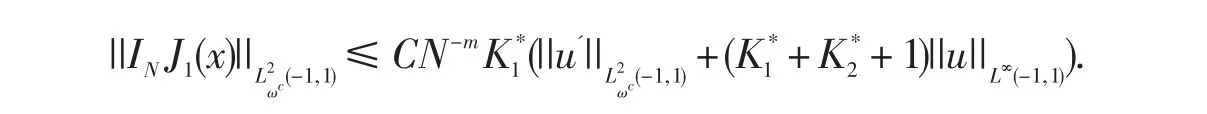
相同的推导过程得到

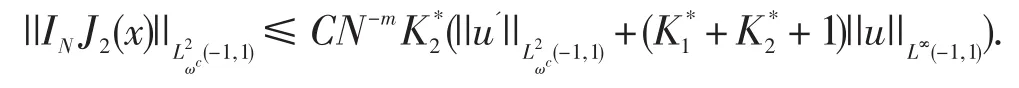
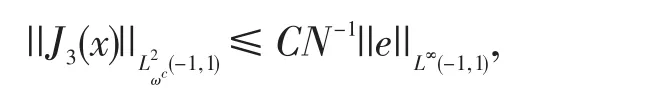
再由定理4.1的结论，有

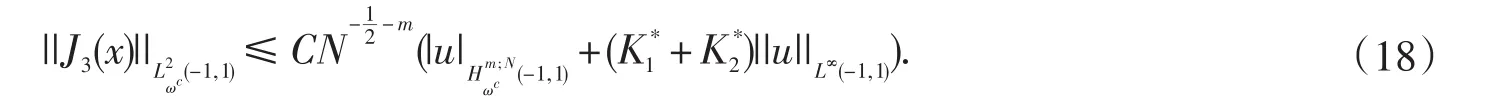
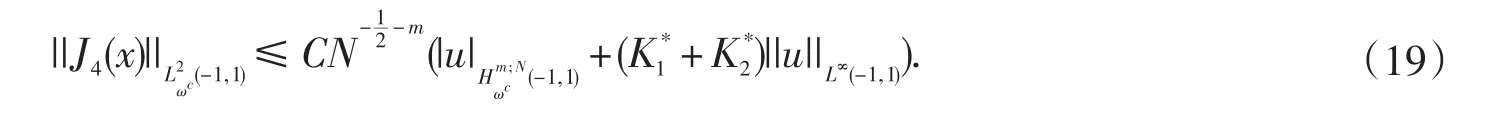
联合以上证明定理结论获证

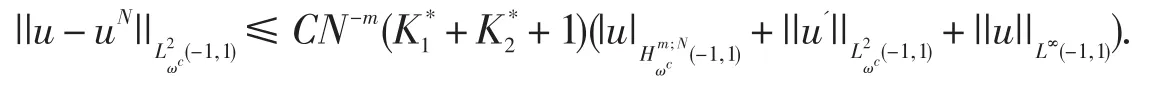
5 算法设计及数值实验

考虑如下形式的方程（1），其中

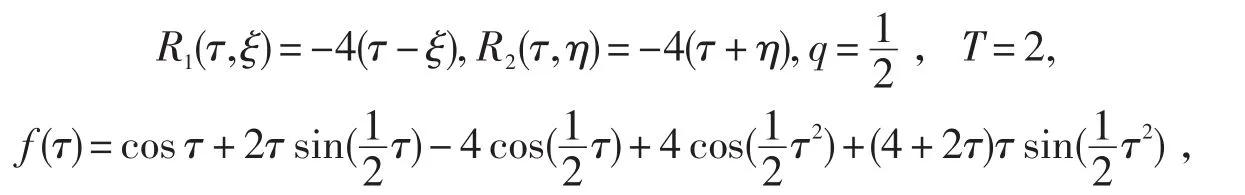
方程的精确解为:y(τ)=cosτ，τ∈[0,2]，其误差表及误差图展示如表1及图1，2所示.

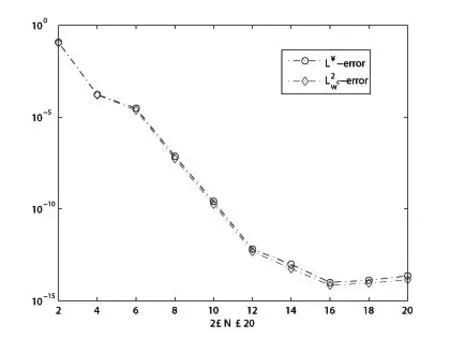
图1 u-uN在L∞和空间的误差

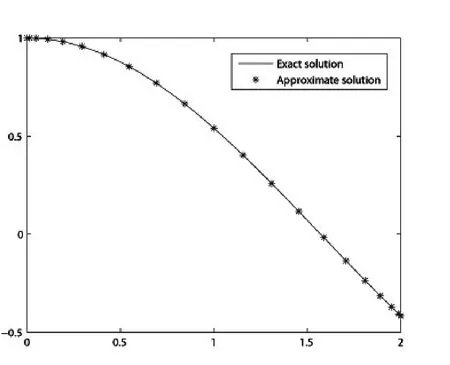
图2 精确解和近似解的对比

表1 u-uN在L∞和空间中的误差

表1 u-uN在L∞和空间中的误差

N误差0.11307 1.6317e-004 2.431e-005 5.5119e-008 1.7854e-010 N24681 0 L∞误差0.1183 1.6916e-004 3.067e-005 7.437e-008 2.5699e-010 L2 ωc ωc 12 14 16 18 20 L∞误差6.5353e-013 9.72e-014 1.0103e-014 1.3267e-014 2.2926e-014误差4.7698e-013 5.6001e-014 7.0571e-015 9.1216e-015 1.4116e-014 L2

[1]TANG T,XU X,CHENG J.On Spectral methods for Volterra integral equation and the convergence analysis[J].J.Comput.Math.,2008,26(6):825-837.

[2]CHEN YP,TANG T.Convergence analysis of the Jacobi spectral-collocation methods for Volterra integral equation with a weakly singular kernel[J].Math.Comput.2010,79(269):147-167.

[3]WAN Z,CHEN Y,HUANG Y.Legendre spectral Galerkin method for second-kind Volterra integral equations[J].Front.Math.China,2009,4(1):181-193.

[4]XIE Z,LI X,TANG T.Convergence Analysis of Spectral Galerkin Methods for Volterra Type Integral Equations[J].J.Sci.Comput,2012,53:414-434.

[5]GU Z,CHEN Y.Chebyshev spectral collocation method for Volterra integral equations[C].Contemporary Mathematics,2013(586):163-170.

[6]LI J,ZHENG W,WU J.Volterra Integral Equations with Vanishing Delay[J].Applied and Computational Mathematics,2015,4(3):152-161.

[7]CANUTO C,HUSSAINI M,QUARTERONI A,et al.Spectral method fundamentals in single domains[M].Germany:Spring-Verlag,2006.

[8]SHEN J,TANG T.Spectral and high-order methods with applications[M].Beijing:Science Press,2006.

[9]MASTROIANNI G,OCCORSIO D.Optional system od nodes for Lagrange interpolation on bounded intervals[J].J.Comput.Appl.Math.,2001(134):325-341.

[10]HENRY D.Geometric theory of semilinear parabolic equations[M].Germany:Spring-Verlag,1989.

[11]KUFNER A,PERSSON L.Weighted inequality of Hardy’s Type[M].New York:World Scientific,2003.

[12]NEVAI P.Mean convergence of Lagrange interpolation[J].Trans.Amer.Math.Soc.,1984(282):669-698.

The Volterra Integral Equation with Linear Delay and Nonlinear Delay

ZHENG Wei-shan
（Colloge of Mathematics and Statistic，Hanshan Normal University，Chaozhou，Guangdong,521041）

This paper is a study of the Volterra integral equation with linear vanishing delay and nonlinear vanishing delay.First,transfer the integral interval[0,T]into interval[-1,1]through the conversion of variables.Then,use the Gauss quadrature formula to get the approximate solutions.Next,propose the Chebyshevspectral-collocation method to solve the equation.With the help of Gronwall inequality and some other lemmas,a rigorous error analysis is provided for the proposed method,which shows that the numerical error decay exponentially in the infinity norm and the Chebyshev weighted Hilbert space norms.In the end,numerical example is given to confirm the theoretical result.

Chebyshev spectral-collocation method；linear delay；non-linear delay；Volterra integral equations；error analysis.

O 242.2

A

1007-6883（2017）03-0015-08

责任编辑朱本华周春娟

2017-04-05

中山大学广东省计算科学重点实验室开放基金项目（项目编号：2016011）；韩山师范学院扶持项目（项目编号：201404）；韩山师范学院创新强校项目（项目编号：Z16027）．

郑伟珊（1983-），女，广东揭阳人，韩山师范学院数学与统计学院教师，博士.