异质柱形颗粒与球形颗粒混合流动特性的CFD-DEM数值模拟分析

王恒，仲兆平，王佳，王泽宇，王肖祎，朱玲莉



异质柱形颗粒与球形颗粒混合流动特性的CFD-DEM数值模拟分析

王恒1，仲兆平1，王佳1，王泽宇1，王肖祎2，朱玲莉1

(1. 东南大学能源与环境学院，能源热转换及其过程测控教育部重点实验室，江苏南京，210096；2. 东南大学建筑设计院有限公司，江苏南京，210096)

针对成型生物质颗粒与流化介质在气固流化床中的混合流动过程，采用数值模拟对该过程进行描述和分析。应用Fortran语言编程，构建复杂组分的三维气固两相流模型，在介观尺度下对流化床中异质异形颗粒的混合流动模拟问题进行研究。在欧拉和拉格朗日框架下，分别采用不同方法构造柱形颗粒：在CFD模型中，采用虚拟小球法描述柱形颗粒，引入体积分数改进曳力系数公式；在DEM部分，采用球元叠加法构造柱形颗粒，引入软球模型计算颗粒间的碰撞力。基于上述方法，模拟表观气速分别为1.0 m /s和2.0 m/s时的柱形生物质与石英砂混合流动的物理过程，并将模拟结果与试验结果进行对比。研究结果表明：该方法能较好地模拟在鼓泡床状态下异质柱形颗粒与球形颗粒混合流动的过程。

CFD-DEM模拟；柱形颗粒；气固流化床

气固流化床中的颗粒流动模拟是多相流研究中一个重要的领域。气固流化床中的颗粒流动是气流与颗粒之间、颗粒与颗粒之间以及颗粒与壁面之间相互作用的过程，由于固相物料通常不是由单一组分组成，该过程为复杂的异形异质颗粒混合流动过程。针对颗粒在气固流化床中的流动过程，国内外学者已经进行了一些实验和模拟研究，但研究对象多是单组分颗粒。TSUJI等[1−3]将DEM与CFD耦合的方法引入气固流化床领域，成功模拟了单组分球形颗粒的流动过程。桂南[4]应用DEM-LES方法对两相流中的颗粒碰撞问题进行研究，研究对象为单组分的球形颗粒。对于单组分非球形颗粒流动的研究也有相关报道。卢洲等[5]模拟了柱状颗粒在弯管输送过程中的碰撞特性；ZHONG等[6]采用球元叠加的方法构造柱形颗粒并模拟其在喷动床中的流动；REN等[7−9]采用同样的构造方法分别研究了圆柱形颗粒、玉米型颗粒在喷动床中的流动过程。目前针对气固流化床中2种不同颗粒混合流动问题的模拟研究较少。LIU等[10]采用实验方法研究了柱形颗粒与球形颗粒混合流动特性。张勇[11]针对异质球形颗粒和异径球形颗粒在流化床中的混合特性分别进行了探索，YU等[12]采用微动力建模法研究了异径球形颗粒的混合与分离特性。任冰[13]模拟了等密度的非球形颗粒与球形颗粒混合流动情况。上述研究或针对同质异形颗粒或针对异质同形颗粒，而气固流化床中的物料如固体垃圾、生物质燃料等，其形状多为非球形，通常会与煤、河沙等掺混，从而呈现相对复杂的流动特性，因此开展异质非球形颗粒与球形颗粒的混合流动模拟研究工作具有十分重要的意义。

1 柱形颗粒模型

1.1 虚拟小球法

在CFD部分计算气固作用力时，需要考虑柱形颗粒与球形颗粒的差异，采用虚拟小球法模拟CFD部分的柱形颗粒。将柱形颗粒视为多个虚拟小球堆积组成，如图1所示。

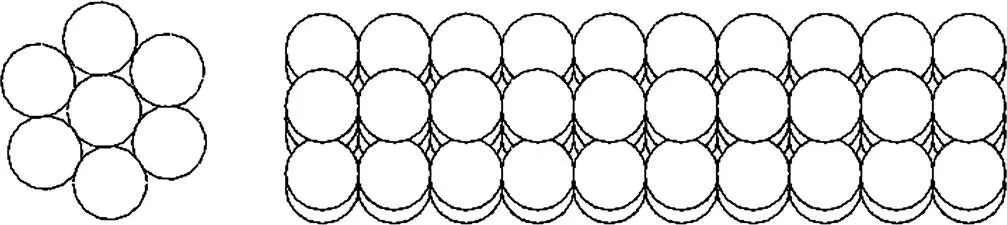
图1 虚拟小球构造柱形颗粒示意图

虚拟小球的直径定义为f，虚拟小球相对于柱形颗粒的体积分数为f，当f足够小，f足够大时，柱形颗粒的体积近似为两者的乘积。此时空隙率为单位网格中除去球形颗粒及虚拟小球体积的部分：

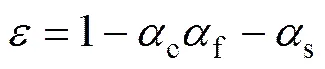
在计算气固作用力时，固相平均速度s计算公式如下：

(2)

式中：c和s分别为柱形颗粒和球形颗粒的体积分数；c和s分别为柱形颗粒和球形颗粒在单位网格内的平均速度。

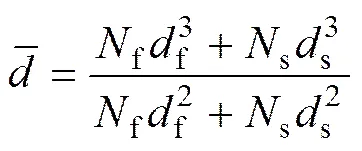
式中：f和s分别为构成柱形颗粒虚拟小球的数量和球形颗粒的数量；f和s分别为构成柱形颗粒虚拟小球的直径和球形颗粒的直径。

1.2 球元叠加法

在DEM部分的计算中，对柱形颗粒采用球元叠加法进行构造。球元叠加法[14]即采用多个小尺寸球形颗粒顺序排列重叠构造成非球形颗粒的方法。图2所示为球元叠加法的示意图，球元的数量和尺寸决定了柱形颗粒的准确程度和计算所用的时间。

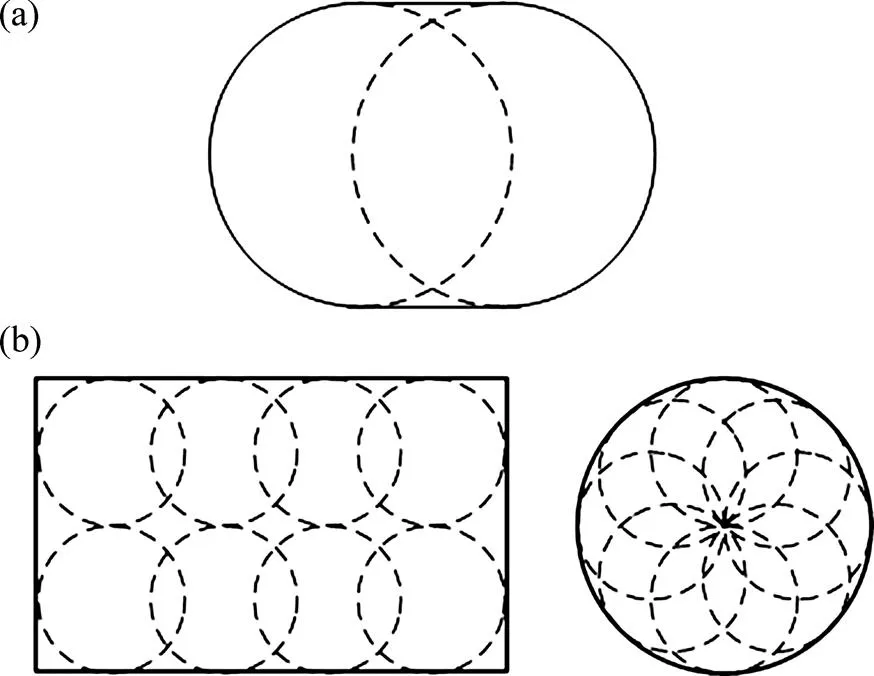
(a) 2球元；(b) 32球元

2 数值模拟方法

在欧拉−拉格朗日框架下，基于CFD-DEM耦合算法，分别建立气相、固相物理模型。由于固相颗粒由异质柱形颗粒和球形颗粒组成，在计算气固作用力以及颗粒碰撞时，不能按照单组分颗粒模型进行处理，本文对有关参数进行了改进。

2.1 气相物理模型

气相流体采用连续性方程与纳维−斯托克斯方程进行描述：

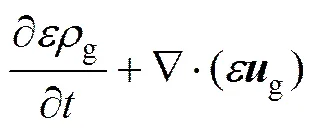
(5)

式中：为单位网格内的空隙率；g为气相密度；g为气相流速；为气相压力；为重力加速度；为应力张量。g为单位网格的气固相互作用转换项：

g=d+m+s(6)

式中：d为曳力；m为Magnus升力；s为Saffman升力，与曳力相比，后两者相对较小，可忽略。

d=(s−g) (7)

式中：为气固曳力系数，可根据空隙率，由Ergun公式[15]或Wen&Yu关系式[16]进行求解，具体表达式如下：

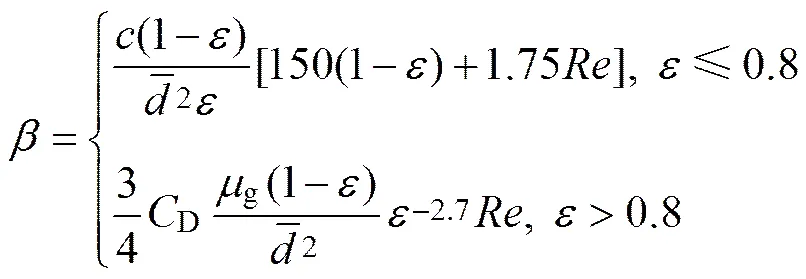
式中：g为气相黏度；为颗粒的平均直径；D为单个球形颗粒曳力系数。

(9)

颗粒雷诺数定义如下：

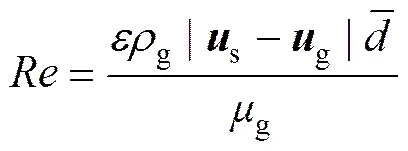
2.2 固相物理模型

固相颗粒的运动在模拟条件下遵循牛顿第二定律，在空间中进行平动和转动，计算公式如下：

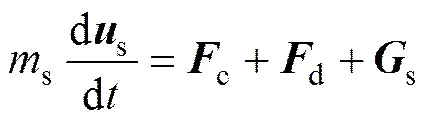
(12)

式中：s为颗粒转动惯量；s为颗粒力矩；s为颗粒质量；s为重力；c颗粒所受的碰撞力；其他作用力在本文计算中不考虑。异质柱形颗粒与球形颗粒的混合运动较传统的DEM模型更为复杂，下面对颗粒碰撞力c和气固曳力d进行详细描述。

2.3 颗粒碰撞模型

颗粒碰撞采用软球碰撞模型，软球模型先计算颗粒下一时间步长的位移，对于球形颗粒，通过比较颗粒质心与两球半径之和(壁面可以看作静止颗粒)，判定是否发生碰撞。对于发生碰撞的颗粒，进一步计算其与周围颗粒或者壁面间的作用力。相对于硬球模型，软球模型允许颗粒同时与多个颗粒及壁面发生碰撞。

将球形颗粒的碰撞受力c分为切向力ct和法向力cn：

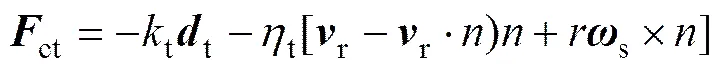
(14)

式中：t和n为切向和法向弹性系数；t和n表示切向和法向的相对位移；t和n分别为切向和法向的阻尼系数；s为颗粒相对角速度；r为颗粒相对线速度。若切向力和法向力之间存在ct＞|s−g|，则发生相对滑移，此时，切向力的计算公式为：

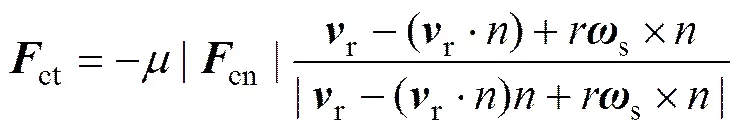
式中：为颗粒碰撞后的摩擦因数。

柱形颗粒由球元构成，同一个柱形颗粒的球元位置相对固定，不存在碰撞。柱形颗粒的碰撞判定思路是判定表面球元的球心之间的距离与半径之和的关系(假设壁面为静止颗粒)。柱形颗粒的碰撞可分为以下6种情况：1) 单个球元与单个球元的碰撞；2) 单个球元与多个球元的碰撞；3) 单个球元与壁面的碰撞； 4) 多个球元与多个球元的平行碰撞；5) 多个球元与多个球元的交叉碰撞；6) 多个球元与壁面的碰撞。

柱形颗粒的碰撞方式虽然不同，但各种碰撞受力分析的基本思路是一致的，即柱形颗粒碰撞受力为其所有球元受力的叠加。

2.4 气固曳力

DEM方法对流场中每一个颗粒的受力都进行了计算，对于球形颗粒，其所受的气固曳力为

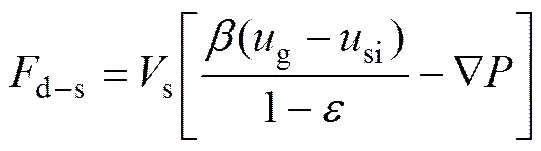
式中：s为球形颗粒的体积；si为球形颗粒的速度。

柱形颗粒所受的气固曳力，为球元受力的叠加，计算公式为

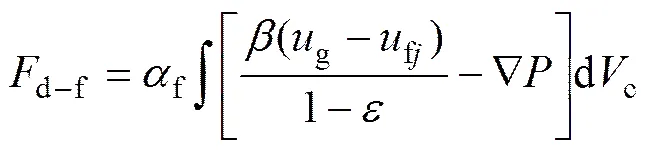
式中：c为柱形颗粒的体积；fi为柱形颗粒的速度。

3 异质柱形颗粒与球形颗粒混合流动模型的建立

基于上述CFD-DEM模拟方法，本课题组以成型生物质颗粒与石英砂混合流动为研究对象，建立了异质柱形颗粒与球形颗粒混合流动的并行计算模型，建立截面长×宽为150 mm×20 mm，高度为1 000 mm的流化床模型，分别计算了表观气速为1.0 m/s和2.0 m/s的混合流动模型，实际计算中，颗粒运动集中在流化床下部，为节省时间，在高度方向上仅计算500 mm以下的颗粒流化过程。

网格尺寸决定了计算域内离散节点的位置，若网格尺寸过大，则计算精度偏低；若网格尺寸过小，则可能使网格尺寸与颗粒粒径的关系将不能满足曳力公式的要求。柱形颗粒由小球或球元构成，小球或球元个数越多，则小球或球元的粒径就越小。因此，本文选择如下计算条件：CFD计算部分的柱形颗粒由2 072个直径为0.8 mm的虚拟小球组成，计算网格尺寸为2 mm，DEM计算部分的柱形颗粒由768个球元叠加而成，球元直径为3 mm，，计算网格尺寸为3 mm。

壁面边界假设为无滑移边界条件；入口采用速度入口边界条件，出口采用压力出口边界条件。布风方式为均匀布风。相关模拟参数见表1。

表1 模拟参数

4 模拟结果分析

4.1 模拟结果与试验瞬态对比

表观气速1.0 m/s的工况模拟结果如图3所示。流化开始时，柱形颗粒与球形颗粒按照坐标进行排列布置，试验测得该工况下的最小流化速度为0.68 m/s。在表观气速1.0 m/s的工况中，固相颗粒有明显的床层界面，颗粒扬起的最大高度约为静止床高的2倍。图3中，颗粒从0 s开始至0.48 s为鼓泡初期，气体进入床层并形成气泡，携带球形颗粒上升，并将顶层柱形颗粒与球形颗粒一并扬起。颗粒随着气泡到达床层表面，气泡破裂后，颗粒被抛向床层上部，达到最高点后回落并再次与上升的气泡相遇，从0.6 s至1.34 s，柱形颗粒与球形颗粒混合良好。图4所示为成型生物质颗粒与石英砂混合流动特性试验瞬态图。图4(a)所示为试验中流化前的颗粒在床中的布置，与模拟对应，所用颗粒没有将柱形颗粒与球形颗粒混合，图4(b)~(e)所示为表观气速1 m/s的成型生物质颗粒与石英砂混合流动瞬态图。图3中0.6 s后的颗粒混合行为与图4中试验拍摄的颗粒流动行为十分相似，颗粒混合效果良好。

4.2 压力波动特性分析

压力波动分析方法是对流化床中的压差进行实时测量，并通过分析其时域和频域变化特性，对气固混合流动特性进行定性分析的一种经典的研究方法。实验中采样频率为100 Hz。将模拟得到的瞬时压力与试验测得的压力脉动信号进行处理，得到柱形颗粒与球形颗粒混合流动试验和模拟的功率谱密度(PSD)，如图5所示。压力脉动信号的功率谱表征的是压力信号的能量在频域上的分布，能量最大的点对应的频率为主频。在1.0 m/s的表观气速下，试验与模拟得到了相似的结果，主频均在2 Hz左右，表明两者具有相似的流化特性。模拟和实验得到的功率谱均集中在0~5 Hz，表明气泡行为对流化的影响占主导地位。

4.3 柱形颗粒与球形颗粒混合特性分析

通过分别统计模拟结果中柱形颗粒和球形颗粒的平均高度，可分析异质柱形颗粒与球形颗粒随时间的混合情况。不同气速下柱形颗粒与球形颗粒平均高度随时间的变化如图6所示。在0.6 s后，不同气速下的柱形颗粒和球形颗粒呈现了相似的分布特性，即柱形颗粒与球形颗粒的高度趋于一致，这表明2种颗粒在0.6 s后混合较好，没有发生分层现象。不同表观气速下，颗粒平均高度在起始流化过程中差异较大：在表观气速较大的工况下柱形颗粒与球形颗粒所达到的最大高度也较高，且达到最大的高度需要的时间也更长，该现象符合本文对颗粒运动的描述。

DEM模拟结果保存了每一个颗粒的运动信息，按照不同的床层高度，统计颗粒沿方向和沿方向的时均速度，可以宏观的分析颗粒的运动状态。图7所示为混合颗粒沿床高方向上的时均速度分布，为了更准确地描述混合颗粒的特性，数据未包括0.6 s前起始流化状态的部分。床宽为150 mm，因此，75 mm处为流化床的中心位置，从75 mm处向两侧观察可以发现，混合颗粒的气速在方向大致对称分布，靠近两侧壁面的颗粒以静止或下落为主，中心区域附近的颗粒则以向上运动为主。不同床层高度的颗粒具有不同的运动规律：低床层(=5~60 mm)的颗粒距离布风板较近，颗粒速度受气相射流的影响较大，在方向中间位置呈现规律性波动；=0 mm和=150 mm附近，颗粒速度为0 m/s或略小于0 m/s，其原因是布风板开口离两侧壁面距离略远，气相对颗粒作用力较小。位于中床层的颗粒(=80~120 mm)在方向中间位置的速度分布与低床层的颗粒类似；但是=0 mm和=150 mm附近，颗粒以一定的速度下落，因为处于中间位置的颗粒向上运动到最大高度时开始从向上作用力较小的两侧位置回落。高床层颗粒的时均速度较小，表明该位置的颗粒可能是已运动到最大高度，处于逐渐停止向上运动和开始向下运动的状态。

图3 柱形颗粒与球形颗粒混合流动模拟瞬态图

(a) 流化前；(b)~(g) 气泡运动过程

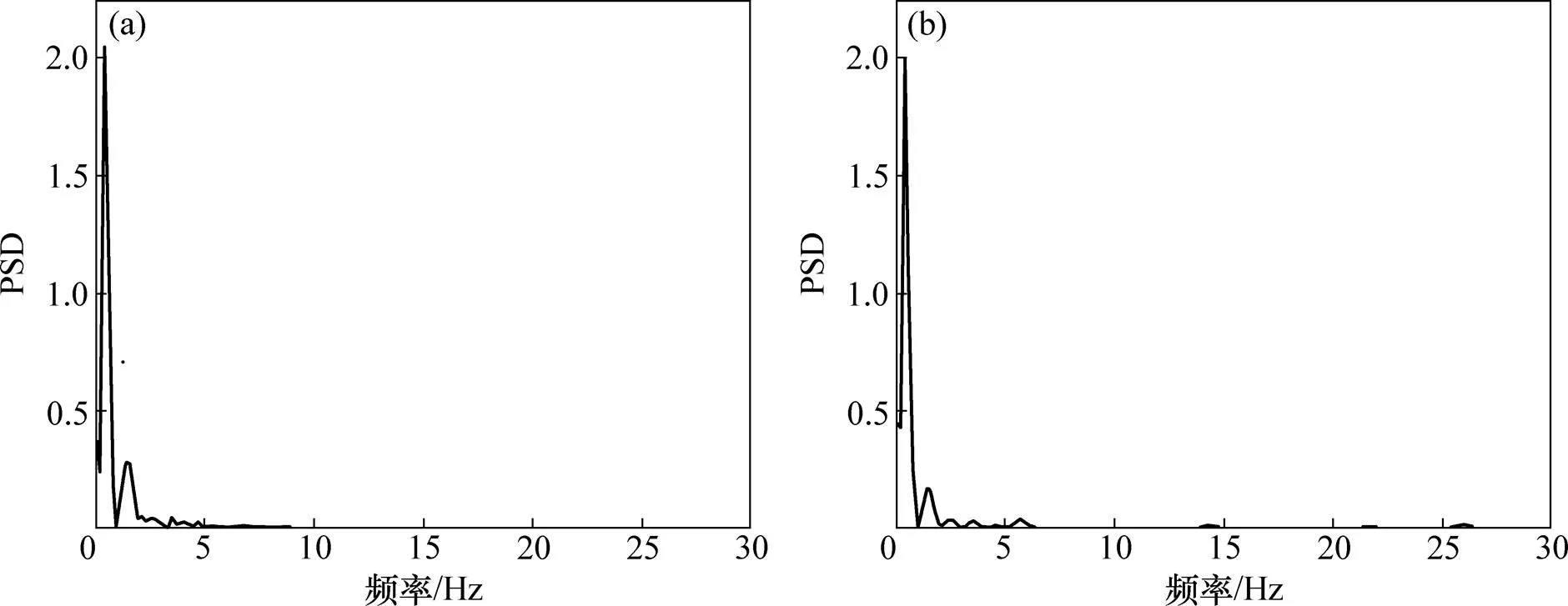
(a) 模拟结果；(b)实验结果

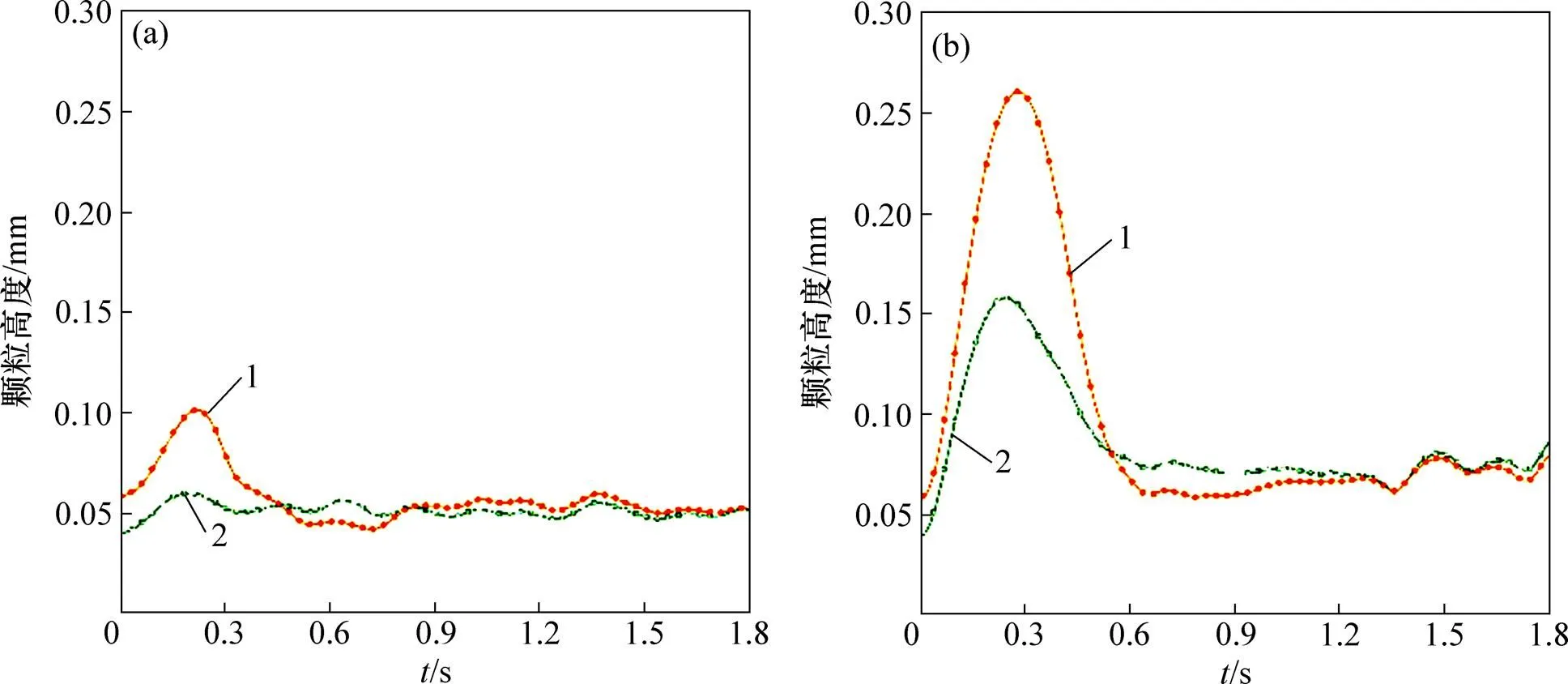
表观气速/(m∙s−1)：(a) 1.0；(b) 2.0

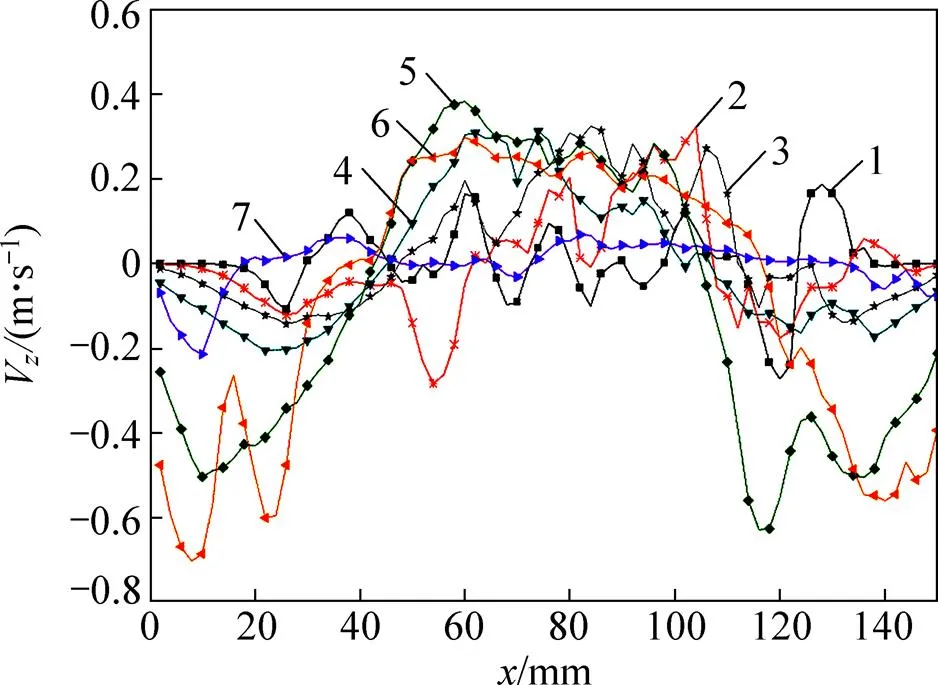
H/mm：1—5；2—20；3—40；4—60；5—80；6—120；7—140。

图8所示为混合颗粒在方向上的时均速度分布。颗粒在低床层时沿方向向床层中心位置(坐标75 mm处为流化床中心位置)移动，即在中心颗粒向上运动后，周围的颗粒向中心位置补充，颗粒在中床层高度(=80~120 mm)沿方向背离中心位置运动，即向两侧壁面处移动，对照图7可知该高度的颗粒呈中间上升两侧下落的状态，图8表明该下落位置的颗粒同时向两侧的壁面位置移动。高床层位置的颗粒在方向没有比较明显的运动。

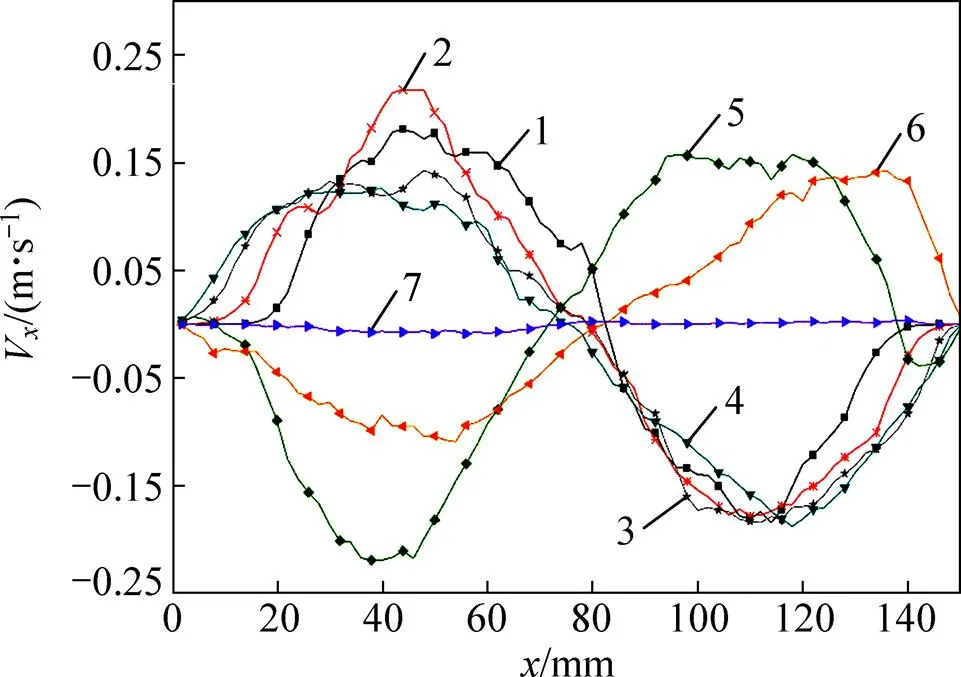
H/mm：1—5；2—20；3—40；4—60；5—80；6—120；7—140。

结合图7和图8可知，方向中间区域(=75 mm)的颗粒从低床层位置向上运动，两侧颗粒向中间区域补充，中间床层位置的颗粒在方向中间区域向上运动同时向远离中间区域的壁面处运动，在两侧靠近壁面的区域向下运动，高床层颗粒呈现到达高点开始回落。床内颗粒整体呈现从中部向上到达高点后两侧回落的运动状态。

图9所示为不同床层高度处的时均空隙率，整体上呈现床高越高，空隙率越大的趋势，颗粒集中在中低床层。从图9可见：低床层的空隙率沿方向波动较大，因为低床层颗粒靠近气流入口，受气体射流的影响显著。

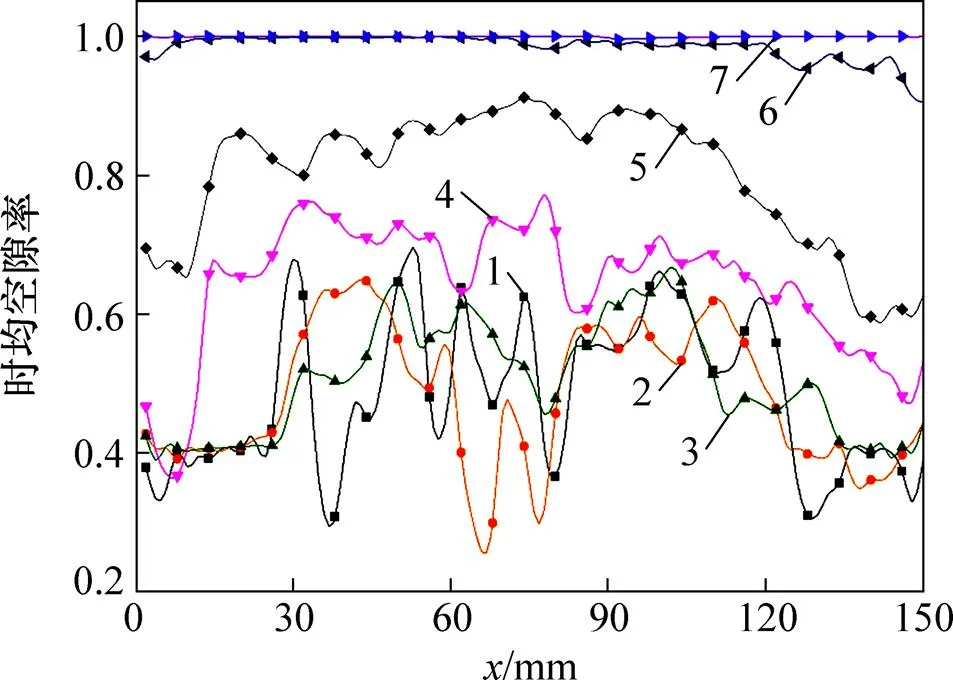
H/mm：1—5；2—20；3—40；4—60；5—80；6—120；7—140。

5 结论

1) 通过构建CFD-DEM模型，采用球元叠加法和虚拟小球法描述柱形颗粒，引入体积分数改进曳力系数公式，实现了柱形颗粒与球形颗粒的混合流动。

2) 模拟结果与试验结果接近，说明该方法能较好地模拟在鼓泡床状态下异质柱形颗粒与球形颗粒混合流动的过程。

3) 随着表观气速的增大，颗粒上升高度增大，异质柱形颗粒与球形颗粒的混合流动整体呈现从中部向上到达高点后两侧回落的周期运动状态，符合实际流化过程中颗粒运动规律。

[1] TSUJI Y, KAWAGUCHI T, TANAKA T. Discrete particle simulation of two-dimensional fluidized bed[J]. Powder Technology, 1993, 77: 79−87.

[2] KAWAGUCHI T, TANAKA T, TSUJI Y. Numerical simulation of two-dimensional fluidized beds using the discrete element method (comparison between the two- and three-dimensional models)[J]. Powder Technology, 1998, 96: 129−138.

[3] GERA D, GAUTAM M, TSUJI Y, et al. Computer simulation of bubbles in large-particle fluidized beds[J]. Powder Technology, 1998, 98: 38−47.

[4] 桂南. 复杂两相流动中颗粒碰撞的DEM-LES/DNS耦合模拟研究[D]. 杭州: 浙江大学热能工程研究所, 2010: 87−107. GUI Nan. Simulation study on DEM-LES/DNS coupling of particle collisions in complex two-phase flows[D]. Hangzhou: Zhejiang University. Institute of Thermal Energy Engineering, 2010: 87−107.

[5] 卢洲, 刘雪东, 潘兵. 基于CFD-DEM方法的柱状颗粒在弯管中输送过程的数值模拟[J]. 中国粉体技术, 2011, 17(5): 65−69. LU Zhou, LIU Xuedong, PAN Bing. Numerical simulation of the process of cylindrical particles in elbow pipe based on CFD-DEM method[J]. China Powder Technology, 2011, 17(5): 65−69.

[6] ZHONG Weiqi, ZHANG Yong, JIN Baosheng, et al. Discrete element method simulation of cylinder-shaped particle flow in a gas-solid fluidized bed[J]. Chem Eng Technol, 2009, 32(3): 386−391.

[7] REN Bing, ZHONG Wenqi, CHEN Yu, et al. CFD-DEM simulation of spouting of corn-shaped particles[J]. Particuology, 2012, 10(5): 562−572.

[8] REN Bing, ZHONG Wenqi, JIANG Xiaofeng, et al. Numerical simulation of spouting of cylindroid particles in a spouted bed[J]. Canadian Journal of Chemical Engineering, 2014, 92(5): 928−934.

[9] REN Bing, ZHONG Wenqi, JIN Baosheng, et al. Numerical simulation on the mixing behavior of corn-shaped particles in a spouted bed[J]. Powder Technology, 2013, 234(1): 58−66.

[10] LIU Xuejiao, ZHONG Wenqi, JIANG Xiaofeng, et al. Spouting behaviors of binary mixtures of cylindroid and spherical particles[J]. Aiche J, 2015, 61(1): 58−67.

[11] 张勇. 气固流化床非球异质颗粒介观混合特性的实验研究与三维DEM直接数值模拟[D]. 南京: 东南大学能源与环境学院, 2010: 15−34. ZHANG Yong. Experimental study of mesoscopic mixing characteristics of non spherical particles in gas-solid fluidized bed and direct numerical simulation of three-dimensional DEM[D]. Nanjing: Southeast University. College of Energy and Environment, 2010: 15−34.

[12] YU A B, FENG Y Q. Microdynamic modelling and analysis of the mixing and segregation of binary mixtures of particles in gas fluidization[J]. Chem Eng Sci, 2007, 62(1/2): 256−268.

[13] 任冰. 稠密气固系统非球形颗粒运动机制的试验和CFD-DEM耦合模拟研究[D]. 南京: 东南大学能源与环境学院, 2013: 91−121. REN Bing. Experimental study on the mechanism of non spherical particle motion in dense gas solid system and CFD-DEM simulation[D]. Nanjing: Southeast University. College of Energy and Environment, 2013: 91−121.

[14] KODAM M, BHARADWAJ R, CURTIS J, et al. Cylindrical object contact detection for use in discrete element method simulations. Part I: contact detection algorithms[J]. Chem Eng Sci, 2010, 65(22): 5852−5862.

[15] ERGUN S. Fluid flow through packed columns[J]. Chem Eng Prog, 1952, 48(2): 89−94.

[16] WEN C Y, YU Y H. Mechanics of fluidization[J]. Chemical Engineering Progress Symposium Series, 1955, 62: 100−111.

(编辑 赵俊)

Simulation study on characteristics of cylinder-shaped particles and sphere-shaped particles flow

WANG Heng1, ZHONG Zhaoping1, WANG Jia1, WANG Zeyu1, WANG Xiaoyi2, ZHU Lingli1

(1. Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education,School of Energy and Environment, Southeast University, Nanjing 210096, China;2. Engineering Design & Research Institute, Southeast University, Nanjing 210096, China)

A numerical simulation method was used to describe and analyze the mixing flow of biomass particle and quartz sands in gas-solid fluidized bed. Three-dimensional gas-solid flow models were constructed to simulate the mixed flow of heterogeneous particles in mesoscopic scale. The integrated model was built in an Eulerian-Lagrangian approach and the constructed methods of cylinder-shaped particles were different when it came to different numerical methods. Each cylinder-shaped particle was constructed as an agglomerate of fictitious small particles in CFD part, while in DEM method, cylinder-shaped particles were built by multi-sphere method, in which small sphere element merged with each other. Soft sphere model was used to get the connect force between particles. The total connect force of cylinder-shaped particle was calculated as the sum of the small sphere particles’ forces. Two models with different superficial gas velocities (1.0 m/s and 2.0 m/s) were built and the results of simulation were compared with the experimental results. The results show that the present work provides an effective approach to simulation the flow of two component particles.

CFD-DEM simulation; cylinder-shaped particle; gas-solid fluidized bed

10.11817/j.issn.1672−7207.2017.06.034

TQ051

A

1672−7207(2017)06−1667−07

2016−06−01；

2016−09−28

国家自然科学基金资助项目(51276040，U1361115)(Projects(51276040, U1361115) supported by the National Natural Science Foundation of China)

仲兆平，博士，教授，从事能源与环境工程研究；E-mail：zzhong@seu.edu.cn