300 M高强钢高温流变行为及本构方程

章晓婷，黄亮，李建军，张轩越，曾嵘，李蓬川



300 M高强钢高温流变行为及本构方程

章晓婷1，黄亮1，李建军1，张轩越1，曾嵘1，李蓬川2

(1. 华中科技大学材料科学与工程学院材料成形与模具技术国家重点实验室，湖北武汉，430074；2. 中国第二重型机械集团公司，四川德阳，618000)

通过Gleeble 3500高温热模拟压缩实验，研究300M高强钢在变形温度900~1 150 ℃、应变速率0.01~10 s−1条件下变形温度和应变速率对材料流动应力的影响规律，建立高温热变形材料本构方程。研究结果表明：变形温度和应变速率对300M钢材料流变应力都有显著的影响，随着变形温度的降低和应变速率的增加，材料流动应力增加；建立了材料常数，，ln和激活能与真应变之间的非线性四项式函数关系；所建立材料本构方程预测值与实验值具有较好的一致性，说明该本构方程能够准确地描述300M钢热变形条件下的材料流变行为。

300M高强钢；热变形行为；本构方程；误差分析

航空工业中起落架是飞机降落装置中的关键受力部件，要承受巨大的载荷及强烈的冲击，直接关系到乘员们的安全，因此起落架的性能对飞机安全起着十分重要的作用。当前世界上95%以上飞机起落架都是采用超高强度钢锻造成形后加工制造而成[1]。作为综合性能良好的飞机起落架用钢之一的300M钢是一种典型的中碳低合金超高强度钢，具有强度高、韧性良好、固有疲劳强度高、疲劳性优良、抗应力腐蚀性能好等优点，因此被广泛地应用于飞机起落架、平尾大轴、机翼主梁等关键承力构件[2]。而300M钢在锻造成形过程中的高温流变行为，往往对飞机起落架成形制造过程有着重要影响。在锻造过程中，300M锻件所需较大的坯料截面尺寸、复杂的加工工艺导致了材料奥氏体晶粒粗大、高温流变行为及本构方程复杂，从而对最终得到的锻件塑性、强度等性能会产生较大的影响。基于此，国内外学者对300M钢进行了大量的研究，刘凯等[3]研究300M钢动态再结晶动力学行为，建立300M钢第一轮动态再结晶和第二轮动态再结晶的峰值应变、临界应变、平均晶粒尺寸和体积分数动力学模型。杜敬霞等[4]对不同条件下的300M钢热变形行为进行研究，建立了包括变形温度、应变速率和应变在内的300M钢高温变形本构方程，并验证了方程的准确性和适用性。黄顺喆等[5]通过对不同变形条件下300M钢高温热压缩金相组织进行观察分析，将其高温流变曲线大致分为动态回复型和动态再结晶型2种。王长健等[6]对300M钢奥氏体晶界腐蚀行为进行了研究。彭雯雯等[7]研究了不同回火温度对300M超强钢显微组织和力学性能的影响，得到在回火温度为300 ℃时材料具有强度、塑性、韧性最优的综合力学性能。赵敬世等[8]研究不同回火温度下回火马氏体位错密度的变化规律，解释了位错密度是影响300M钢获得高强度的主要原因。代伟等[9]采用300M钢流变应力本构模型对飞机起落架外筒模锻成型过程进行仿真。可见：在锻造过程中300M钢再结晶本构模型、热处理工艺等领域的研究已经取得了较大的进展。但关于300M钢热变形条件下的流动应力行为方面的研究仍不够深入，未建立合理的关于不同应变量下的300M钢流变行为本构方程，以便于能够准确描述其关于温度、应变速率、应变之间的关系。本文作者通过300M钢高温热模拟压缩实验，研究变形温度、应变速率及应变对材料流动应力影响规律，揭示不同变形温度和应变速率条件下的热变形行为，建立300M钢高温热变形条件下双曲正弦形式的Arrhenius应力应变本构关系，并采用4种统计分析指标分析验证本构方程的准确性和适用性。研究结果不仅为后续数值模拟提供了可靠的材料流动变形参数，也为300M钢在锻造热加工后获得所要求的组织结构和性能的研究和实际生产中热变形工艺参数的优化起指导作用。

1 实验材料与方法

1.1 实验材料

实验材料为中国第二重型机械集团提供的锻坯300M钢，其化学成分如表1所示。实验使用的试样为直径×长度8 mm×12 mm圆柱体试样。

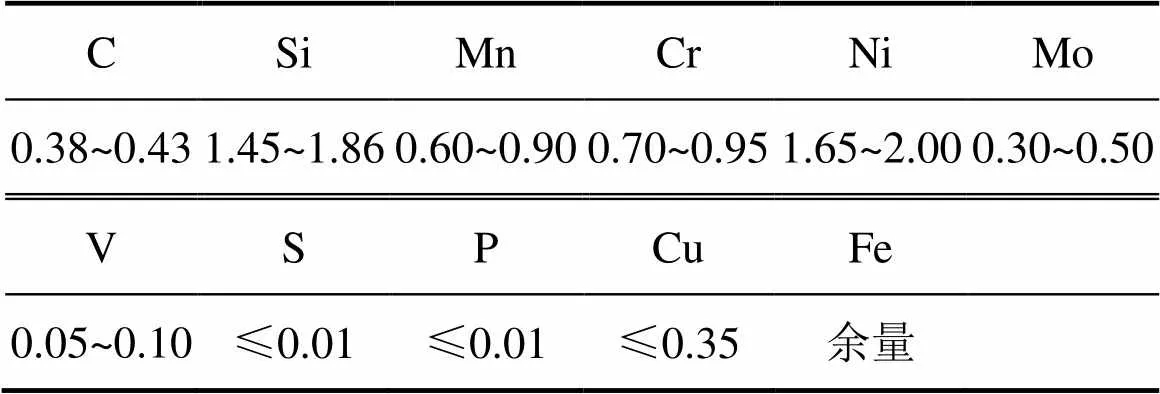
表1 300M钢的化学成分(质量分数)

1.2 实验方法

根据实际生产工艺成形温度范围为850~1 180 ℃，设定高温热模拟实验工艺参数变形温度为900，950，1 000，1 050，1 100，1 150 ℃，应变速率为0.01，0.1，1，10 s−1，试样的变形量为60%。热模拟压缩实验在抽真空充氩气的保护气的Gleeble 3500试验机上进行，具体高温热模拟实验过程如图1所示。首先将300M钢试样以10 ℃/s的升温速率加热到1 150 ℃并保温4 min，使得试样奥氏体组织均匀化。然后再以10 ℃/s的速率降温到变形温度，试样继续保温1 min，用来消除内部由于降温过程导致的温度梯度，随后按照设定的变形温度和应变速率下进行压缩变形，在压缩量达到60%时迅速水淬冷却。

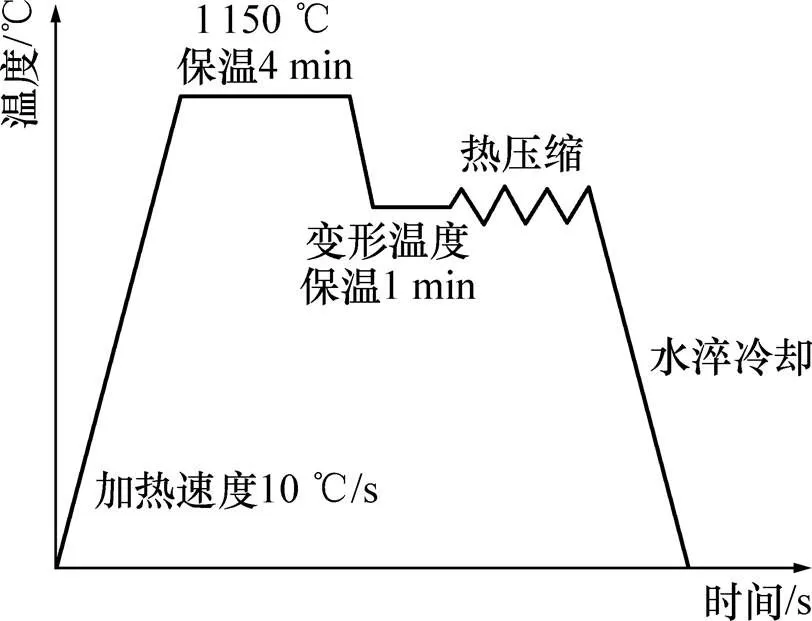
图1 300M钢热压缩实验过程

2 结果与分析

2.1 材料流变行为

在不同的变形温度和应变速率下，300M钢高温热压缩变形时的应力应变曲线如图2所示。从图2可以看出：在不同的变形条件下的300M钢真实应力应变曲线在形状上大致相似。当应变速率一定时，随着变形温度的降低，材料流动应力增加；当变形温度一定时，随着变形速率的增大，材料流变应力增加。在整个压缩变形过程中，300M钢流变行为主要分为以下4个阶段：加工硬化阶段、过渡阶段、软化阶段和稳态流变阶段。在材料热变形的初始阶段，材料内部以加工硬化为主，随着应变的增加，位错密度增加，导致流变应力迅速增大。当应变达到再结晶临界应变时，由于材料内部动态回复或动态再结晶等软化机制的作用，此作用抵消了一部分加工硬化，使得材料流变曲线斜率逐渐减小；最后由于加工硬化和动态软化机制达到动态平衡，流变应力也维持在一个相对恒定状态。

从图2(a)可知：在应变速率为0.01 s−1、变形温度为950~1150 ℃时，300M钢的应力应变曲线为双峰不连续再结晶型，而且第二应力峰值明显大于第一应力峰值。分别由图2(b)和2(c)可知，在应变速率为0.01 s−1、变形温度为900~950 ℃和应变速率为0.1 s−1、变形温度为950~1 150 ℃时，应力应变曲线呈现出单峰不连续再结晶现象，变形过程中存在着最大应力；从图2(b)，2(c)和2(d)可以看出：在应变速率0.1 s−1、温度为900~950 ℃和应变速率为1和10 s−1、变形温度为950~1 150 ℃时，应力应变曲线呈现动态再回复型，全部不存在应力峰值情况。

2.2 临界应变分析

动态回复型应力应变曲线不存在应力峰值，通过求取动态再结晶临界应变c的计算方法，再根据临界应变c=p(其中：p为峰值应变，取值为0.8[10])，继而获得动态再结晶型的峰值应变p。借助求取曲线临界应变c的方式间接建立300M钢高温变形条件下的峰值应力本构方程。

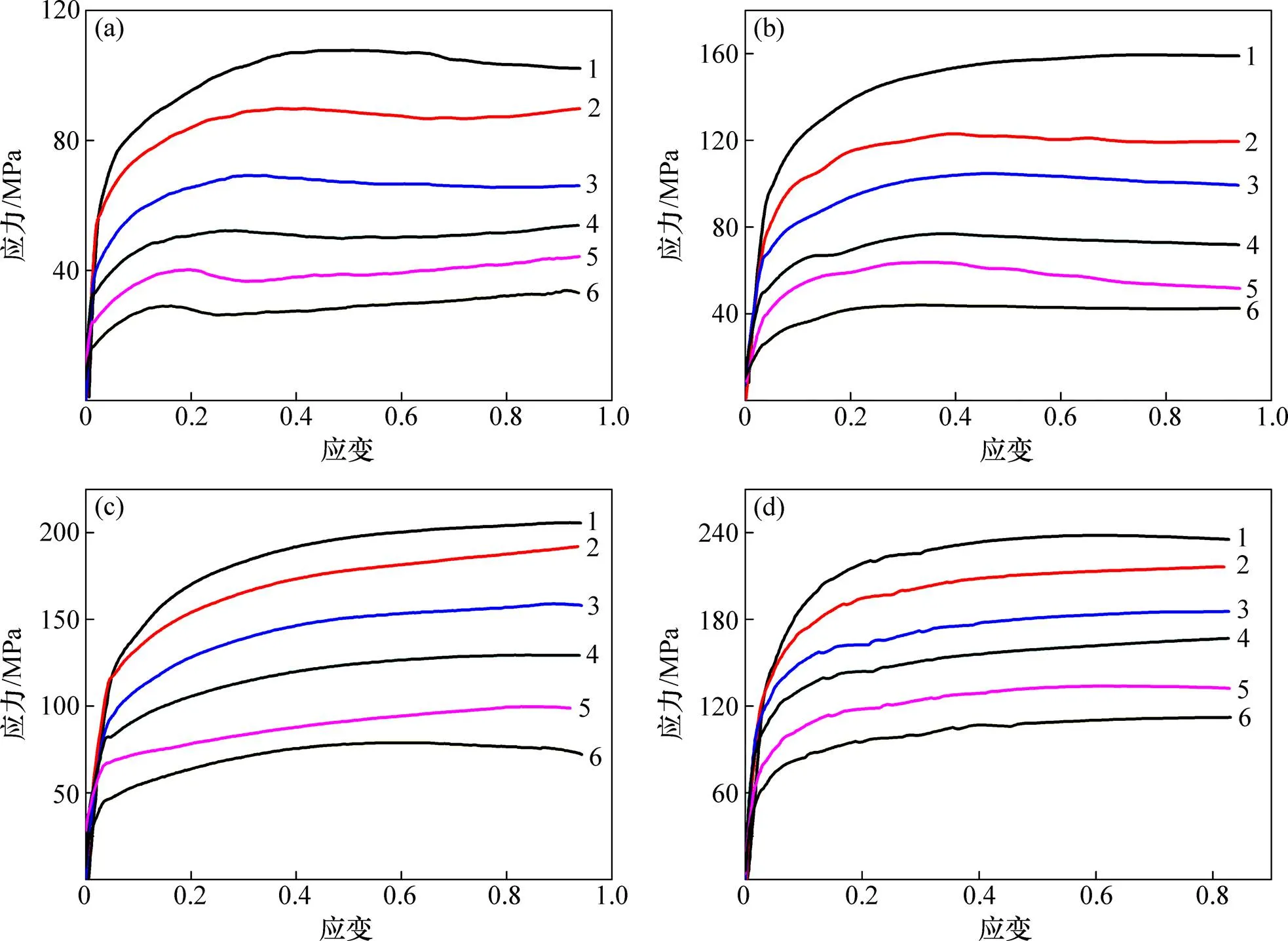
(a) 0.01 s−1；(b) 0.1 s−1；(c) 1 s−1；(d) 10 s−1

临界应变c通过应力−应变曲线上的材料加工硬化率的变化规律来确定，POLIAK等[11]认为材料发生再结晶时，其−曲线呈现出拐点就是临界应变c。下面以求不同温度下应变速率为10 s−1的临界应力为例。首先，用差分法处理高温热压缩模拟实验应力应变曲线，所取的应变范围为0.02~0.4，得到不同温度的加工硬化速率与应力之间关系如图3所示；然后进一步求取−(d/d)−曲线的极小值点来求得拐点c，−(d/d)与应力之间关系如图4所示。

由图4可以看出：高温变形初期材料内部位错密度较低，随着应力的增加位错密度不断增加，故加工硬化速率变化率(d/d)增大；接着原处于滑移面上的位错开始滑移和攀移发生动态回复作用(即曲线的第1个拐点位置处)，导致加工硬化速率变化率减小。随后加工硬化作用再次大于动态回复作用，曲线加工硬化速率变化率再次上升。最后在(d/d)与应力的拐点临界应力c时，材料内部发生动态再结晶作用，动态软化作用机制再次大于加工硬化，位错密度的减少，所以加工硬化速率变化率再次下降。

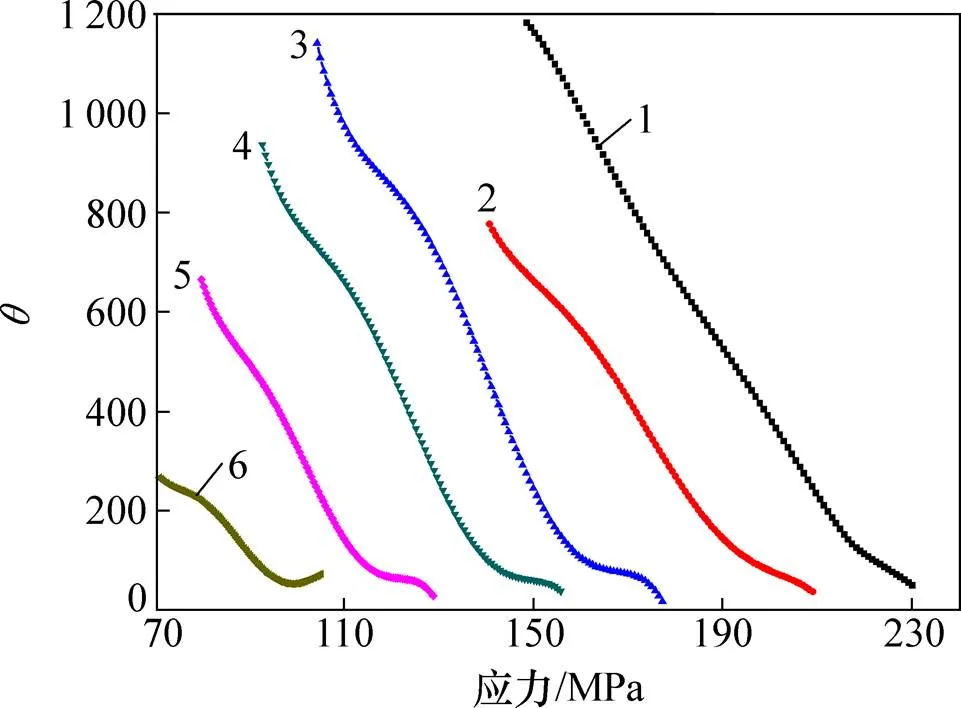
1—900℃；2—950℃；3—1 000℃；4—1 050℃；5—1 100℃；6—1 150℃。

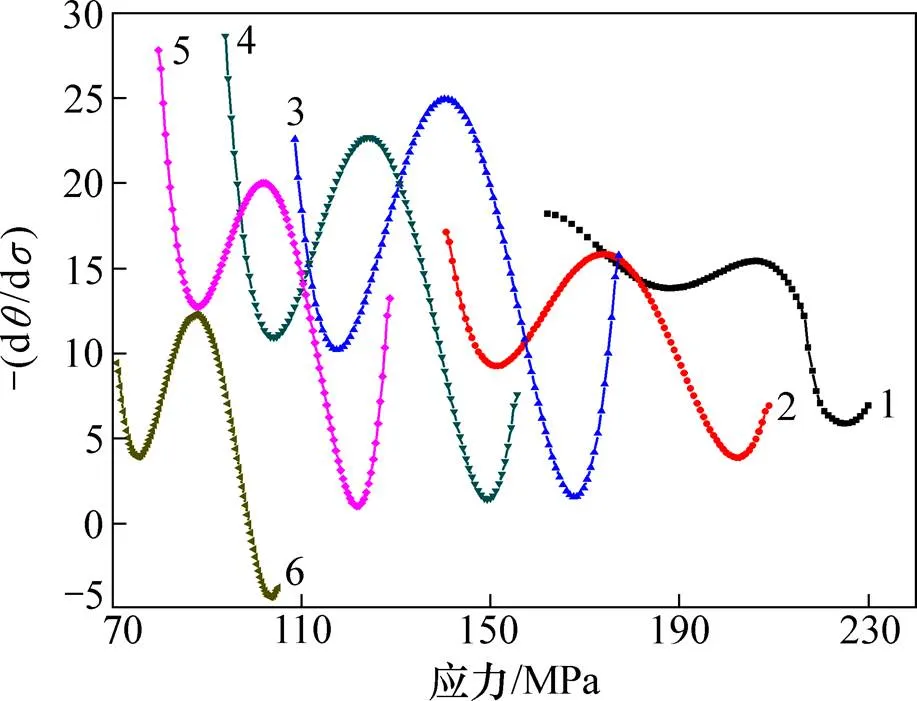
1—900℃；2—950℃；3—1 000℃；4—1 050℃；5—1 100℃；6—1 150℃。

采用以上求取临界应变的方法，分别得到变形温度为900~1 150 ℃时不同变形条件下300M钢回复型曲线动态再结晶的临界应变c，峰值应变p，临界应力c，峰值应力p结果如表2所示。从表2可见：随着变形温度的降低和应变速率的增大，材料的再结晶的临界应力c和峰值应力p均增大。

表2 不同的变形条件下300M钢的c，p，c，p

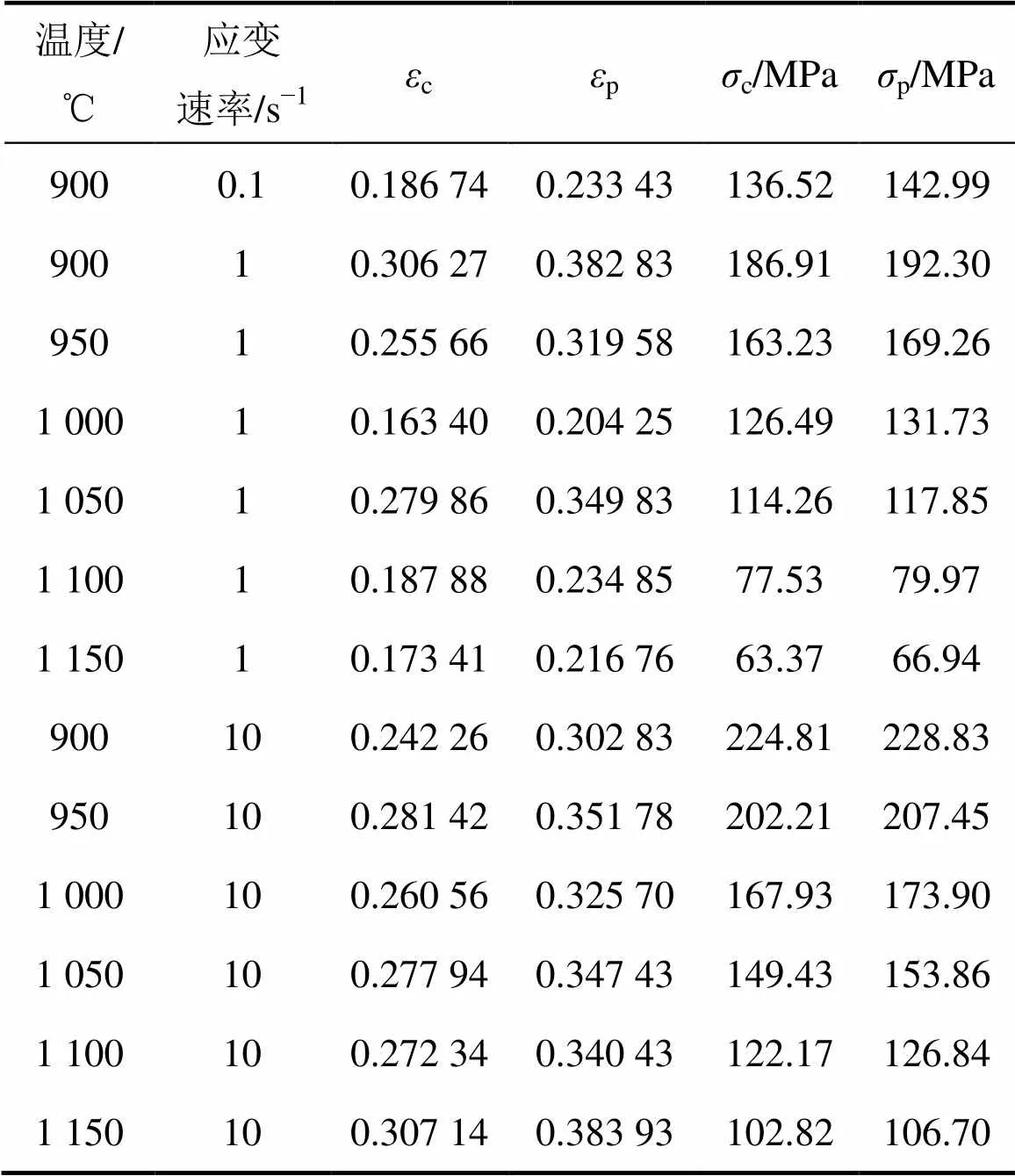
Table 2 σc, σp, εc, εp of 300M steel under different deformation conditions

2.3 本构方程的建立

当材料成分确定时，在高温热变形过程中，材料流变应力与变形温度，应变速率相关[12−14]。

低应力水平时，＜0.8，流变应力和应变速率呈指数关系：

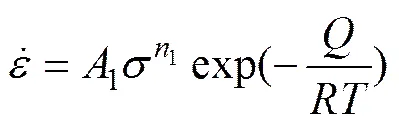
高应力水平时，＞1.2，流变应力和应变速率呈现幂指数关系：

(2)

整个应力范围内流变应力和应变速率呈现双曲正弦Arrhenius函数关系：

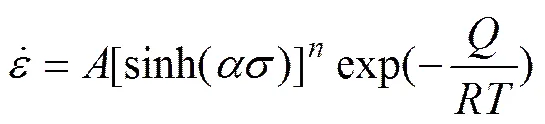
在金属和合金的热加工变形中，材料高温塑性变形时应变速率受热激活过程控制，建立了流变应力、应变速率和变形温度的关系[15]：

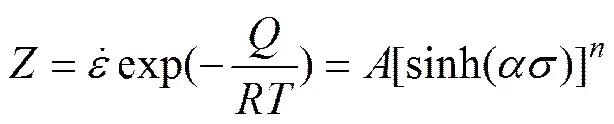
式中：为Zener-Hollomon参数，即温度补偿的应变速率因子。

对式(1)和(2)两边分别取对数得到：

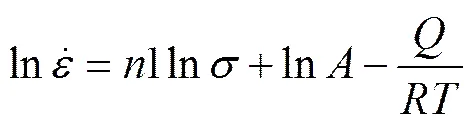
(6)

对式(3)两边取对数得到：

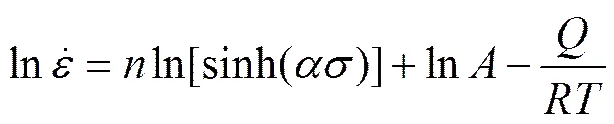
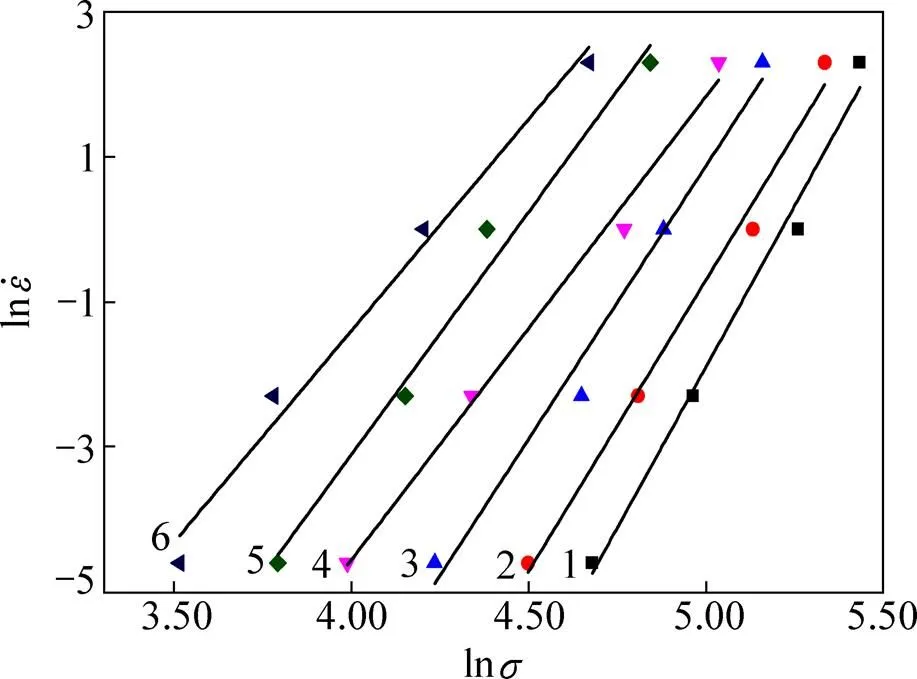
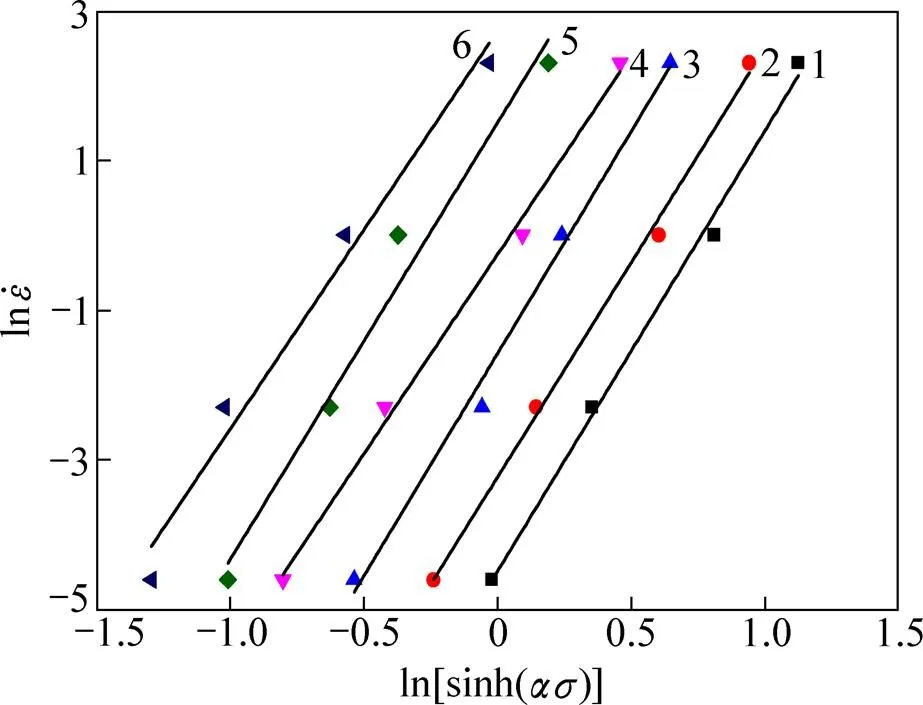
将不同温度下的300M钢的峰值应力、已求的以及相应的应变速率代入式(7)，得到关系曲线如图7所示。可以得到直线斜率平均值=5.684 3。

1—900℃；2—950℃；3—1 000℃；4—1 050℃；5—1 100℃；6—1 150℃。

图5 不同变形条件下300M钢线性关系

Fig. 5 Linear relationship betweenandof 300M steel under different deformation conditions

1—900℃；2—950℃；3—1 000℃；4—1 050℃；5—1 100℃；6—1 150℃。

1—900℃；2—950℃；3—1 000℃；4—1 050℃；5—1 100℃；6—1 150℃。

当变形速率一定时，将式(7)整理可得

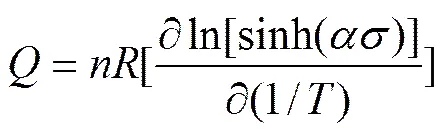
对式(4)两边取对数式可得

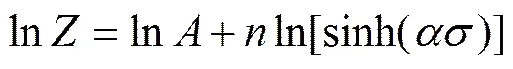
将不同变形温度下的应变速率和求得的代入式(4)中得到。绘制出关系曲线如图9所示。线性回归直线的截距ln=37.509 8，因此结构因子=1.951 2×1016。一元线性回归可得关系曲线的相关系数′=0.994 37，显然说明式中采用变形温度和应变速率表示的参数用于描述变形过程中峰值流变应力的变化有较高的精度，可以采用变形温度和应变速率定量地描述流变应力峰值的关系。

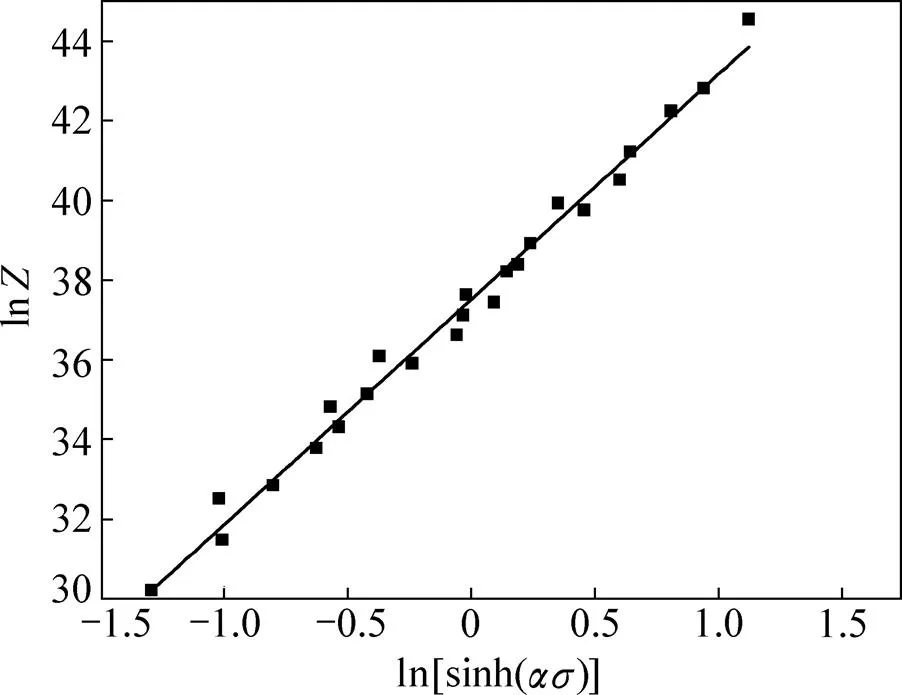
图9 ln Z−的线性关系

将所得系数代入式(3)中得到300M钢双曲正弦形式的Arrhenius本构方程如下式所示：

一般情况下，应变对热变形过程中的流变行为影响微不足道，从而在式(1)~(3)中均没有考虑应变。但是研究表明，应变对，，ln及变形激活能等材料常数具有较大的影响[16−17]。因此，考虑到应变补偿的影响，建立，，ln及变形激活能等参数与真应变的非线性多项式函数关系。通过以上求取对数的计算方法，分别计算了应变为0.1~0.8范围内(相邻间隔为0.1)一系列本构方程的材料常数，，ln及变形激活能。

对4个材料常数与应变之间的关系进行了多项式拟合，结果表明四次多项式能较准确地描述它们之间的关系。当多项式次数小于四阶时，由于拟合方程阶数过低本构方程准确度较差；而当多项式次数大于四阶时，由于过度拟合方程失去了代表性和概括性。相关材料常数，，ln及变形激活能与应变之间的关系如图10所示。最终建立的300M钢材料常数关于应变关系的四项式方程式为

2.4 本构方程的验证

为了验证获得的300M钢的双曲正弦形式Arrhenius本构方程的准确性和可靠性，利用所建立的本构方程，计算出不同变形条件下的峰值应力理论值。300M钢不同变形条件下的理论峰值应力与实验峰值应力对比如图11所示。从图11可见：理论峰值应力与实验峰值应力相关系数为′=0.994 58。并且计算得到预测的最大相对误差为12.82%，最小相对误差为0.32%。平均相对误差为4.10%。由此说明本文建立的300M钢双曲正弦形式的Arrhenius本构方程精度 较高。

为了验证材料常数，，ln及与真应变的非线性函数及由其所建立相关本构方程的准确性，将实验所获得的300M钢流动应力应变曲线与本构模型的应力应变曲线进行对比，如图12所示。从图12可以发现：本文所建立的本构关系与实验获得的应力应变曲线基本上吻合，说明建立的双曲正弦形式Arrhenius本构方程有着较好的准确性和适用性。

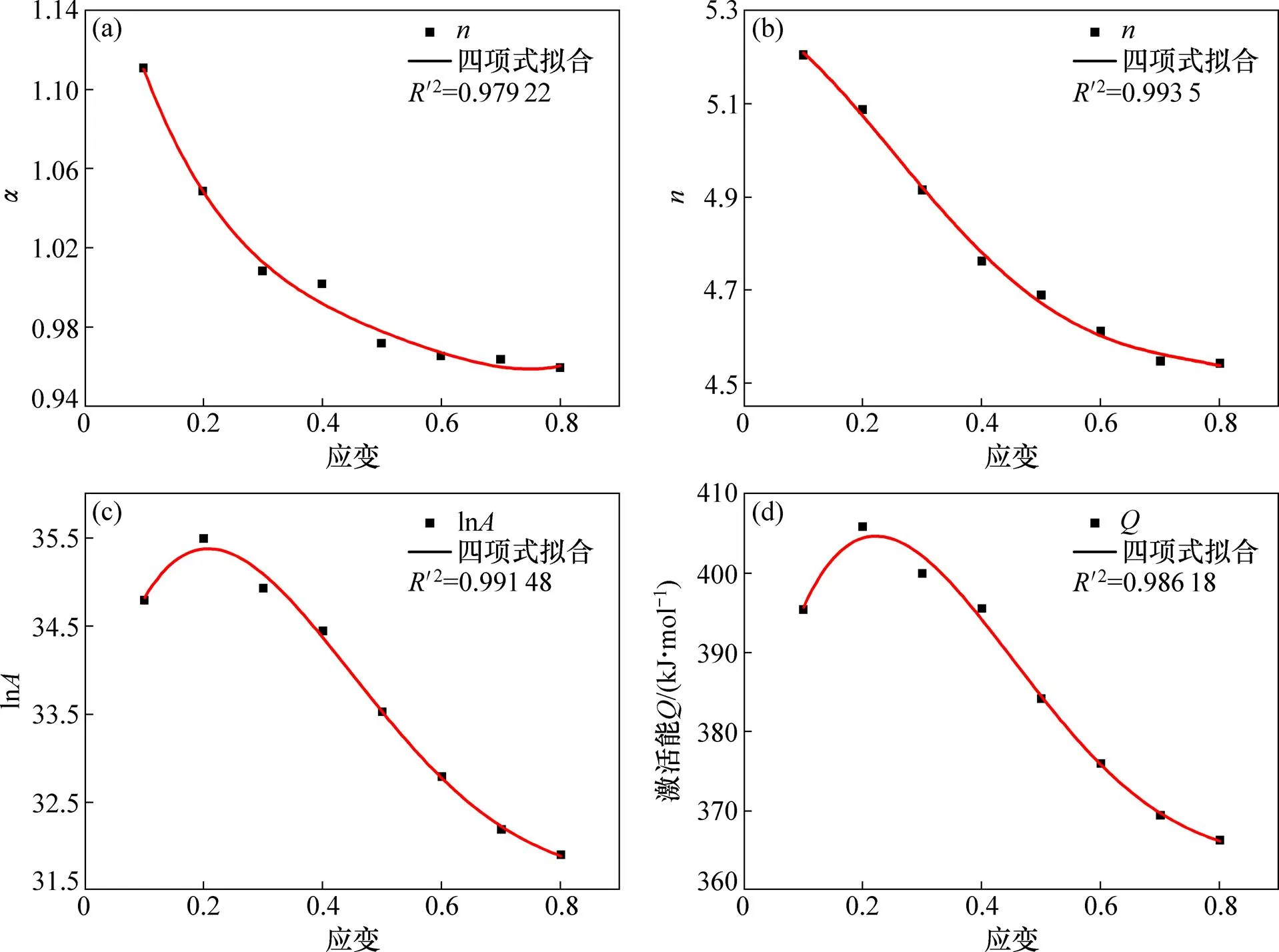
(a) α；(b) n；(c) ln A；(d) Q

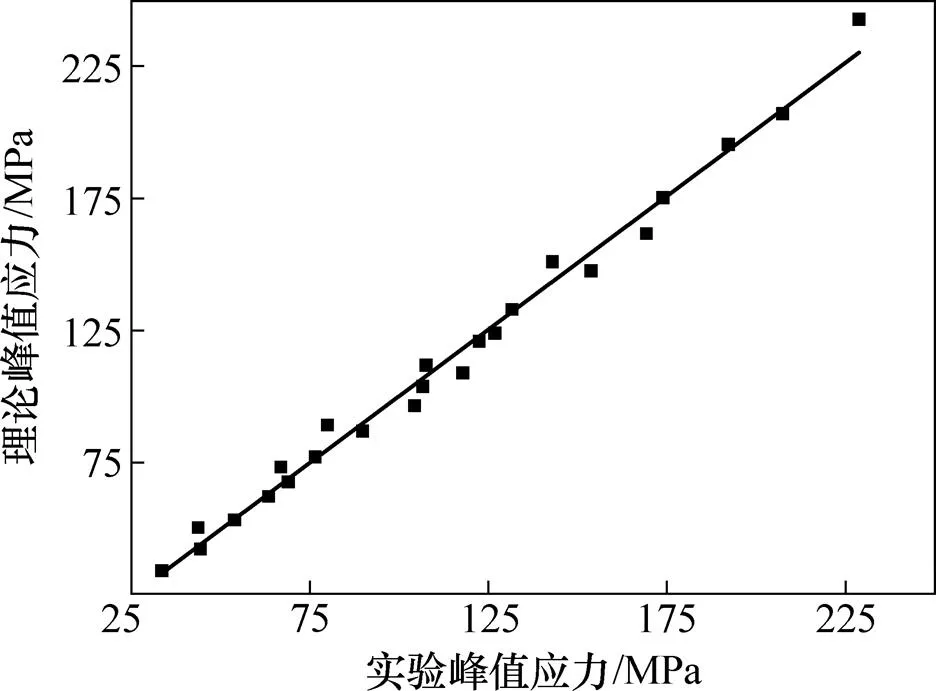
图11 Arrhenius本构方程理论峰值应力与实验峰值应力对比

为了准确评估300M钢本构方程的适用性，分别使用相关系数′、均方根误差RMSE、平均相对误差AARE和标准偏差NMBE 4种统计分析指标对不同变形速率下300M钢热模拟理论值与实验值进行分析。分析结果如表3所示，从表3可知：在不同热变形条件下，线性相关系数′在0.984 86与0.998 29之间，较好地集中分布在最优线′=1上，说明理论值与实验值之间有着较好的相关性。由于误差分析指标RMSE和AARE均在可允许的相对误差10%以内，说明建立的本构方程具有较高的精度，可以为后续的数值模拟提供较好的理论研究指导。而NMBE反映了300M钢理论值与实验值之间的偏差，当NMBE数值为正时，说明平均理论值小于实验值，反之，则说明平均理论值大于实验值，NMBE为−0.007 887~0.034 468之间，说明300M钢本构方程平均理论值与实验值接近。因此，以上4种标准统计学分析参数定量地评价了所建立的本构方程准确性，进一步地说明该本构方程适用于高温变形条件下300M钢材料流变行为分析。

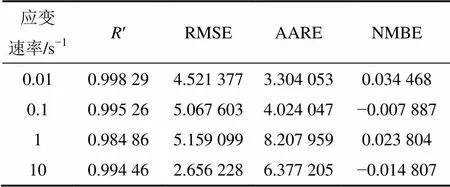
表3 300M本构模型理论值与实验值统计分析

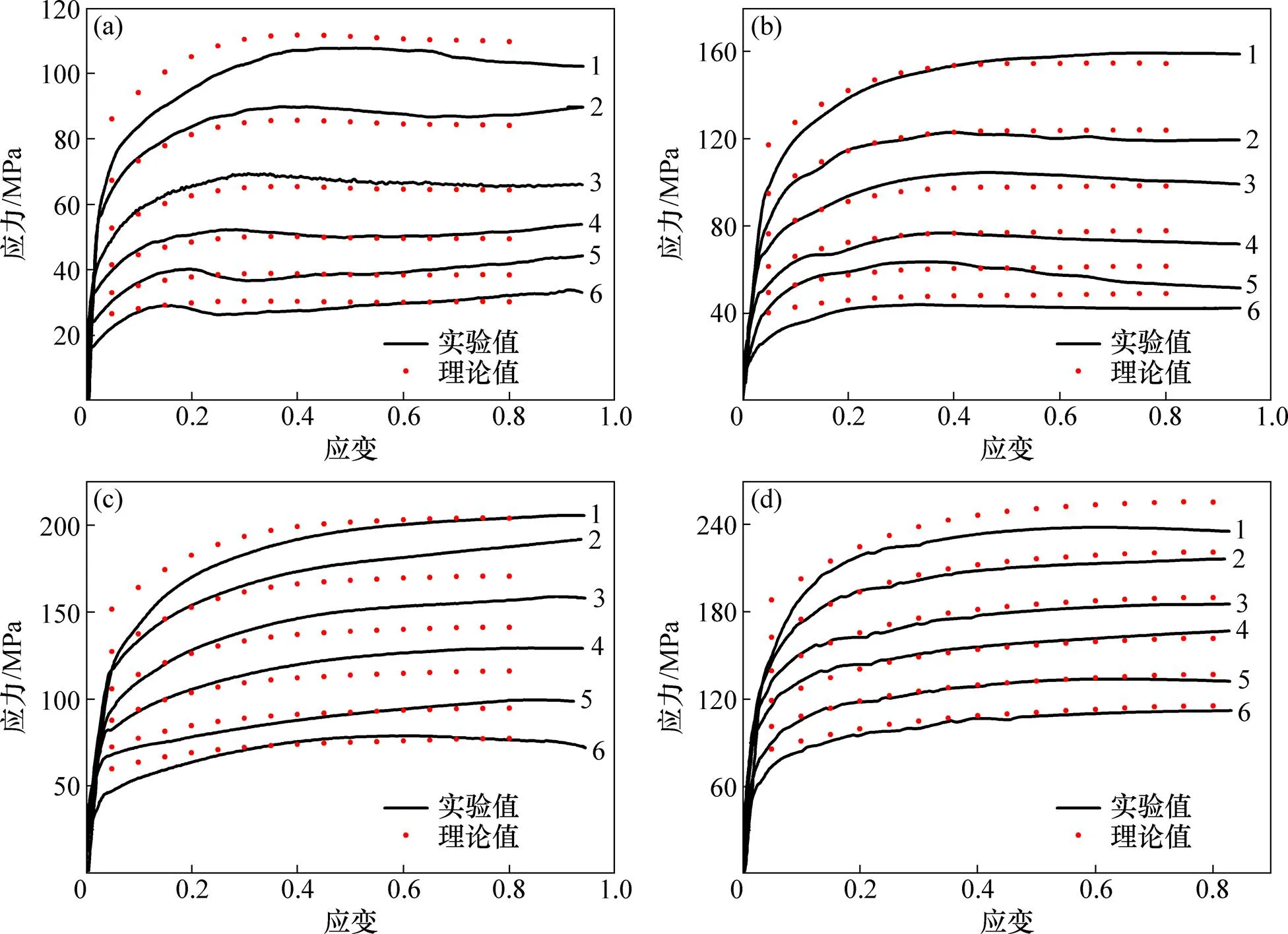
(a) 0.01 s−1；(b) 0.1 s−1；(c) 1 s−1；(d) 10 s−1

3 结论

1) 恒定变形温度条件下，随着变形速率的增加，300M钢流变应力增加；恒定应变速率条件下，随着变形温度的降低，300M钢流动应力增加。300M钢流变应力曲线主要呈现出加工硬化和动态软化2种特征，在不同的变形条件下主要分为不连续双峰再结晶型、单峰不连续再结晶型和动态再回复型3种。

2) 300M钢的高温热变形行为受到热激活能控制，其变形激活能=411.92 kJ/mol。建立300M钢压缩热变形条件下的双曲正弦Arrhenius本构方程为。通过本构方程预测值与实验值对比得到平均相对误差为4.10%。

3) 建立材料常数，，ln，与真应变非线性四项式函数关系，并通过相关系数′，平均相对误差AARE，均方根误差RMSE和标准偏差NMBE验证所建立关于温度、应变速率和应变的材料本构方程预测值与热模拟实验值之间具有较好的一致性，说明本文建立的本构方程能够较为准确地描述300M钢热变形条件下的材料流变行为。

[1] 李华文, 张宝玲, 陈磊. 赵振业院士访谈[J]. 航空发动机, 2009, 35(3): 1−4. LI Huawen, ZHANG Baoling, CHEN Lei. Interview of academician Zhao Zhen-ye[J]. Aeroengine, 2009, 35(3): 1−4.

[2] 张慧萍, 王崇勋, 杜煦. 飞机起落架用300M超高强钢发展及研究现状[J]. 哈尔滨理工大学学报, 2011, 16(6): 73−76. ZHANG Huiping, WANG Chongxun, DU Xu. Aircraft landing gear with the development of 300M ultra high strength steel and research[J]. Journal of Harbin University of Science and Technology, 2011, 16(6): 73−76.

[3] 刘凯, 鲁世强, 欧阳德来, 等. 300M钢动态再结晶动力学[J]. 塑性工程学报, 2012, 19(3): 82−87. LIU Kai, LU Shiqiang, OUYANG Delai et al. Investigation on dynamic recrystallization kinetics of 300M steel[J]. Journal of Plasticity Engineering, 2012, 19(3): 82−87.

[4] 杜敬霞, 李洪波, 张艳姝, 等. 300M高强钢的热变形本构关系研究[J]. 锻压技术, 2014, 39(8): 109−114. DU Jingxia, LI Hongbo, ZHANG Yanshu, et al. Investigation on constitutive relationship of 300M high strength steel during hot deformation[J]. Forging & Stamping Technology, 2014, 39(8): 109−114.

[5] 黄顺喆, 厉勇, 王春旭, 等. 300M钢的热变形行为研究[J]. 热加工工艺, 2010, 39(20): 25−28. HUANG Shunzhe, LI Yong, WANG Chunxu, et al. Investigation on hot deformation behavior of 300M steel[J]. Hot Working Technology, 2010, 39(20): 25−28.

[6] 王长健, 王钢. 300M钢晶粒度腐蚀方法研究[J]. 大型铸锻件, 2004 (3): 13−16. WANG Changjian, WANG Gang. The research for the grain size corrosion method of 300M steel[J]. Heavy Casting and Forging, 2004 (3): 13−16.

[7] 彭雯雯, 曾卫东, 康超, 等. 热处理工艺对300M超高强度钢组织和性能的影响[J]. 材料热处理学报, 2012, 33(3): 94−98. PENG Wenwen, ZENG Weidong, KANG Chao, et al. Effect of treatment on microstructure and properties of 300M ultrahigh strength steel[J]. Transactions of Materials and Heat Treatment, 2012, 33(3): 94−98.

[8] 赵敬世, 张利民. 300M钢回火过程中位错密度变化[J]. 北京航空航天大学学报, 1991(1): 14−17. ZHAO Jingshi, ZHANG Limin. The dislocation density changes of 300M steel in the tempering process[J]. Journal of Beijing University of Aeronautics and Astronautics, 1991(1): 14−17.

[9] 代伟, 易幼平, 李蓬川, 等. 300M超强钢起落架外筒模锻件锤锻工艺[J]. 宇航材料工艺, 2012, 42(6): 100−104. DAI Wei, YI Youping, LI Pengchuan, et al. Hammer forging process for 300M ultra high strength steel die forging of landing gear cylinder[J]. Aerospace Materials and Technology, 2012, 42(6): 100−104.

[10] SELLARS C M, WHITEMAN J A. Recrystallization and grain growth in hot rolling[J]. Metal Science, 1979, 13(3/4): 187−194.

[11] POLIAK E I, JONAS J J. Initiation of dynamic recrystallization in constant strain rate hot deformation[J]. ISIJ international, 2003, 43(5): 684−691.

[12] JONAS J J, SELLARS C M, TEGART W J M. Strength and structure under hot-working conditions[J]. Metallurgical Reviews, 1969, 14(1): 1−24.

[13] ZENER C, HOLLOMON J H. Problems in non-elastic deformation of metals[J]. Journal of Applied Physics, 1946, 17(2): 69−82.

[14] TAKUDA H, FUJIMOTO H, HATTA N. Modeling of flowing stress of Mg-Al-Zn alloys at elevated temperatures[J]. Journal of Materials Processing Technology, 1998, 80(8): 513−516.

[15] 魏洁, 唐广波, 刘正东. 碳锰钢热变形行为及动态再结晶模型[J]. 钢铁研究学报, 2008, 20(3): 31−35. WEI Jie, TANG Guangbo, LIU Zhengdong. Hot deformation and dynamic recrystallization models of C-M steel[J]. Journal of Iron and Steel Research, 2008, 20(3): 31−35.

[16] HU H E, ZHEN L, YANG L, et al. Deformation behavior and microstructure evolution of 7050 aluminum alloy during high temperature deformation[J]. Materials Science and Engineering A, 2008, 488(1/2): 64−71.

[17] ASHTIANI H R R, PARSA M H, BISADI H. Constitutive equations for elevated temperature flow behavior of commercial purity aluminum[J]. Materials Science and Engineering: A, 2012, 545: 61−67.

(编辑 赵俊)

Flow behaviors and constitutive model of 300M high strength steel at elevated temperature

ZHANG Xiaoting1, HUANG Liang1, LI Jianjun1, ZHANG Xuanyue1, ZENG Rong1, LI Pengchuan2

(1. State Key Laboratory of Materials Processing and Die & Mould Technology,School of Materials Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China;2. China National Erzhong Group Co., Deyang 618000, China)

In order to study the effect of deformation temperature and strain rate on the flow stress of 300M high strength steel, isothermal hot compression was tested by Gleeble 3500 thermal simulation machine under environment with temperatures varying from 900 to 1 150 ℃ and strain rates ranging from 0.01 to 10 s−1. The constitutive equation of 300M steel was established on the empirical models. The results show that deformation temperature and strain rate have a significant influence on the flow stress behavior of 300M steel. The material flow stress increases with the decreases of deformation temperature and the increase of strain rate. A nonlinear quadrinomial function is proposed to define the relationship between material constants,, lnand activation energyand strain. The predicted flow stress values using the proposed constitutive equation have a good agreement with the experimental values, which illustrates that the established constitutive equation can accurately describe the rheological behavior of 300M steel on deformation conditions.

300M high strength steel; thermal deformation behaviors; constitutive model; deviation analysis

10.11817/j.issn.1672−7207.2017.06.005

TG142.33

A

1672−7207(2017)06−1439−09

2016−06−09；

2016−09−28

国家自然科学基金资助项目(51435007)；欧盟第七框架居里国际人员交流研究项目(318968)(Project(51435007) supported by the National Natural Science Foundation of China; Project(318968) supported by the EC FP7 Marie Curie Actions-International Research Staff Exchange Scheme)

黄亮，博士，副教授，从事先进金属材料塑性成形技术研究；E-mail：huangliang@hust.edu.cn