临界剪切应力系数曲线适用性研究
孙 昊 周良道 郭伟毅 李三平 / SUN Hao ZHOU Liangdao GUO Weiyi LI Sanping(上海飞机设计研究院,上海201210)(Shanghai Aircraft Design and Research Institute, Shanghai 201210, China)
临界剪切应力系数曲线适用性研究
孙 昊 周良道 郭伟毅 李三平 / SUN Hao ZHOU Liangdao GUO Weiyi LI Sanping
(上海飞机设计研究院,上海201210)
(Shanghai Aircraft Design and Research Institute, Shanghai 201210, China)
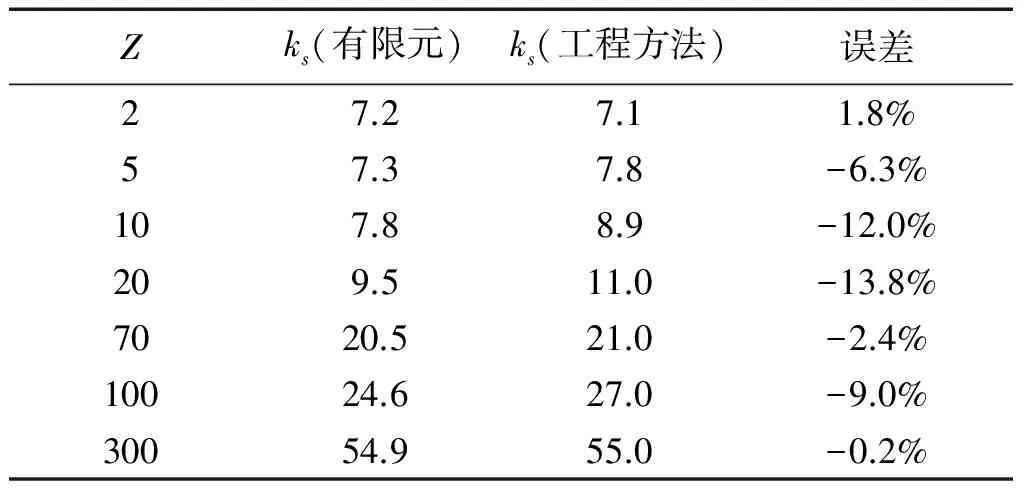
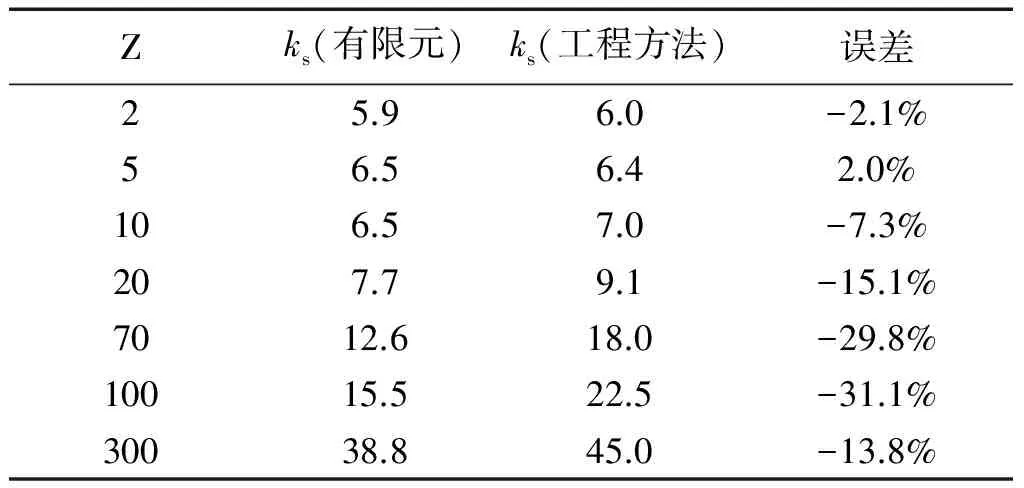
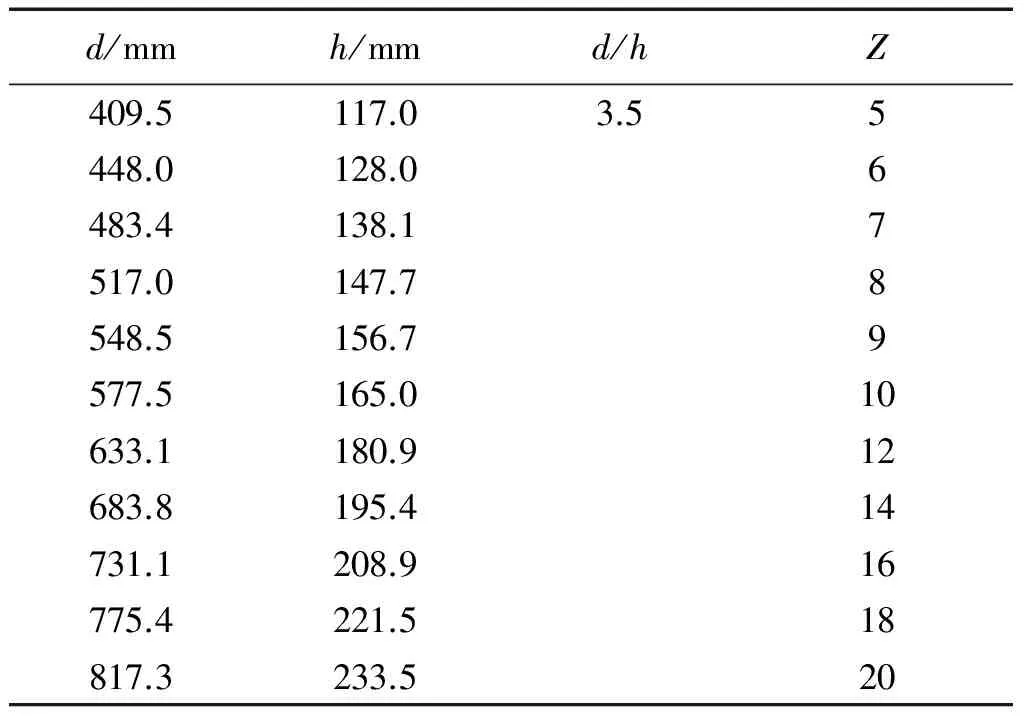
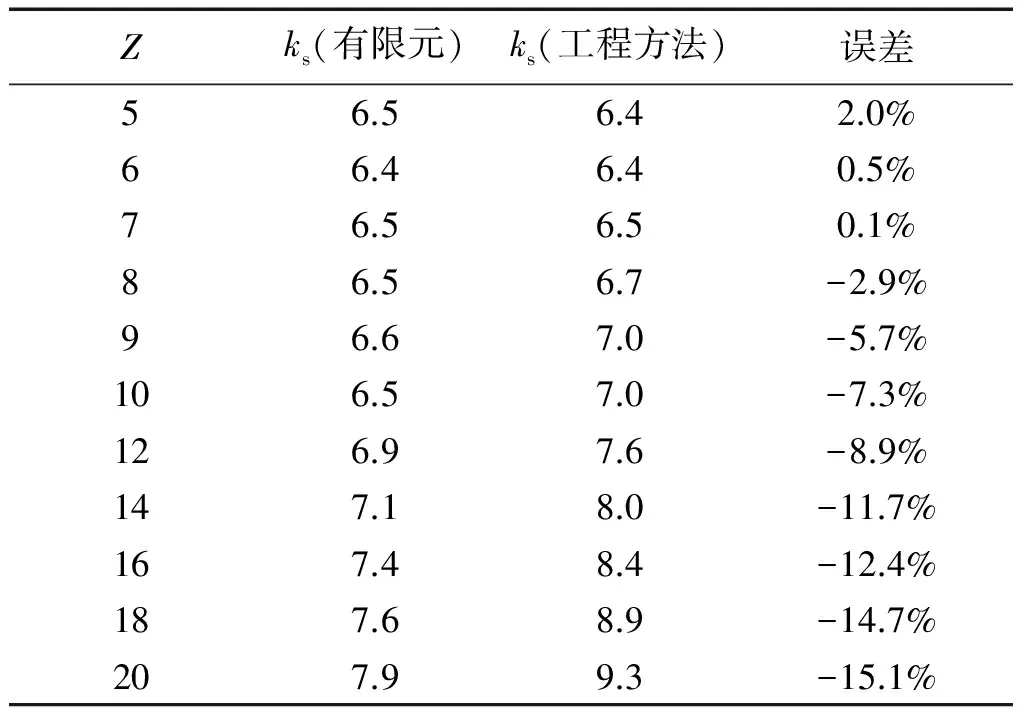
曲板的屈曲问题与材料的弹性模量和泊松比有关,对于机身蒙皮材料2060-T8E30,曲板临界剪切应力系数曲线的适用性有待研究。基于Abaqus的线性静力分析中的Buckle算法,以机身蒙皮材料2060-T8E30建立了多种构型曲板,对比有限元分析值和曲板临界剪切应力系数曲线,通过分析误差,得出结论:对于2060-T8E30材料,可以认为d/h=1.5的ks(曲板临界剪切应力系数)曲线相比有限元分析值偏高,误差不大于15%;d/h=2的ks曲线相比有限元分析值偏高,误差不大于20%;d/h=3.5的ks曲线相比有限元分析值偏高,误差不大于35%。在飞机机身结构常用的参数,即d/h=3.5,Z≤20的情况下,当Z<10时,ks曲线的适用性较好,误差不大于10%;当10 曲板;临界剪切应力系数曲线;有限元;适用性 结构稳定性在飞机结构设计中至关重要,尤其是对于机身壁板,因为薄壁结构的静强度破坏中很大一部分是由结构失稳引起的。然而科学研究和工程实践发现,对于某些类型的结构,屈曲并不等于失稳破坏,比如加筋壁板。机身壁板属于加筋曲板,曲板的蒙皮很薄,蒙皮受剪屈曲之后会产生倾斜的波纹[1],并进入半张力场状态,对角张力系数与临界剪切应力相关。 曲板的临界剪切应力与材料、厚度、轴向长度、环向长度、曲率半径、边界支持条件,临界剪切应力系数等相关。另外屈曲点的判定也有很多种选择,不同的判定方式对初始缺陷的敏感度不同,从而使试验结果有偏差。 为了验证NACA TN 2661的临界剪切应力系数曲线对于机身蒙皮材料2060-T8E30的适用性,选取了常用的曲板构型,用HyperMesh建立了有限元模型,利用Abaqus的Buckle线性静力分析得到曲板的临界剪切特征值,从而计算出临界剪切应力系数,然后对比NACA TN 2661的临界剪切应力系数曲线,分析有限元计算结果和工程曲线的误差。 根据NACA TN 1348[2],曲板的临界剪切应力由式(1)给出: 式中:ks为临界剪切应力系数,由壁板几何构型和边界条件确定;D为单位长度壁板的屈曲刚度(N·mm);μ为泊松比;b为曲板轴向或环向长度的较小值(mm);t为曲板厚度(mm)。 壁板的屈曲刚度D表示为: 根据NACA TN 2661[3],曲板的曲率参数Z表示为: 式中:E为弹性模量(MPa);R为曲板的曲率半径(mm)。 此处,h为曲板环向长度(mm),即桁距;d为曲板轴向长度(mm),即框距,且h 图2表示的是简支曲板的临界剪切应力系数-曲率参数的ks-Z曲线。 临界剪切应力τcr可以写成[4]: 或 目前,民用飞机机身蒙皮典型结构中,曲板的几何构型为:曲率半径R=1 980 mm,厚度t=1.3mm;选取一系列不同的环向长度h和轴向长度d,见表1。 2060-T8E30材料的弹性模量E=72 400MPa,泊松比μ=0.33。 d/h选取了1.5、2、3.5,对应图2中给出的这三种取值的对应曲线;Z选取了2、5、10、20、70、100、300这样的整数,图2中横坐标Z是对数刻度,Z取整数,易于确定其准确位置;纵坐标同样是对数刻度,尽量选取纵坐标易于确定的点,减小观察引起的误差。 3.1 有限元模型的建立 本文将矩形曲板简化为壳单元组成的二维模型,单元类型为S4R,网格大小约10mm,利用HyperMesh平台对表1中的11种曲板构型分别做有限元模型,用以计算不同构型曲板的临界剪切应力。D=175.5mm、h=117mm、d/h=1.5、Z=5的曲板为例,其有限元模型如图3所示。 3.2 边界条件和加载方式 曲板的边界条件是四边简支,在Abaqus中使用柱坐标系,约束设置为:四边U1=0,并且一角U2、U3=0,另一角U3=0。表示四边的径向位移为0,并且一角的环向和轴向位移为0,另一角的轴向位移为0,如图4所示。 曲板的加载方式是四边均布剪切载荷q=1N/mm,如图5所示。 使用的分析步类型是“Buckle”,特征值求解器选用的是“Lanczos”,可以快速求解屈曲载荷特征值,易收敛[5]。 3.3 有限元计算结果及误差分析 3.3.1 计算过程示例 以d=175.5、h=117、d/h=1.5、Z=5的曲板为例,其一阶至三阶屈曲特征值的应力云图如图6~图8所示。 式中:λ为屈曲载荷特征值,q为均布剪切载荷kN/mm,t为曲板厚度(mm)。 经计算得到示例曲板的临界剪切应力的有限元分析值: 根据曲板的几何构型d/h=1.5、Z=5,在图2中读取临界剪切应力系数ks=7.8。 根据误差计算公式: 计算误差为:-6.3%。 3.3.2d/h=1.5的曲板 表2 曲板临界剪切应力系数计算值对比 经过观察分析,误差绝对值多数超过5%,由图9可以看出在Z=20附近,ks的有限元分析值和工程方法曲线读取值偏离程度较大,工程方法曲线读取值普遍高于有限元分析值。对于2060-T8E30材料,可以认为d/h=1.5的曲板临界剪切应力系数曲线相比有限元分析值偏高,误差不大于15%。 3.3.3d/h=2的曲板 表3 曲板临界剪切应力系数计算值对比 经过观察分析,误差绝对值多数超过5%,由图10可以看出在Z>10时,ks的有限元分析值和工程方法曲线读取值偏离程度较大,工程方法曲线读取值普遍高于有限元分析值。对于2060-T8E30材料,可以认为d/h=2的曲板临界剪切应力系数曲线相比有限元分析值偏高,误差不大于20%。 3.3.4d/h=3.5的曲板 表4 曲板临界剪切应力系数计算值对比 经过观察分析,误差绝对值多数超过5%,由图11可以看出在Z>20时,ks的有限元分析值和工程方法曲线读取值偏离程度较大,工程方法曲线读取值普遍高于有限元分析值。对于2060-T8E30材料,可以认为d/h=3.5的曲板临界剪切应力系数曲线相比有限元分析值偏高,误差不大于35%。 3.3.5 飞机常用曲板构型 由于飞机机身结构常用的d/h值为3.5,曲率参数Z在20以下,为了验证d/h=3.5,Z≤20时的临界剪切应力系数曲线的适用性,选取d/h=3.5,Z=5~20的一部分整数,计算其对应曲板的临界剪切应力系数ks,与临界剪切应力系数曲线读取的ks对比,分析误差。曲板构型如表5,计算结果见表6。 表5 d/h = 3.5,Z = 5~20的曲板构型 表6 Z = 5~20的曲板临界剪切应力系数计算值对比 当Z<10时,误差绝对值不超过10%。对于2060-T8E30材料,可以认为d/h= 3.5的曲板临界剪切应力系数曲线的适用性较好,误差不大于10%。 本文基于Abaqus的线性静力分析中的Buckle算法,对蒙皮材料2060-T8E30建立了多种构型曲板,进行了有限元分析和工程方法分析的对比,验证了曲板临界剪切应力系数曲线的适用性。 对d/h= 1.5、d/h= 2、d/h= 3.5的三种典型d/h的曲板,每种分别选取Z = 2、5、10、20、70、100、300七种曲率参数进行模型构建,验证了21种构型的曲板临界剪切应力系数曲线的适用性。 结果表明:对于2060-T8E30材料,可以认为d/h= 1.5的曲板临界剪切应力系数曲线相比有限元分析值偏高,误差不大于15%;d/h= 2的曲板临界剪切应力系数曲线相比有限元分析值偏高,误差不大于20%;d/h=3.5的曲板临界剪切应力系数曲线相比有限元分析值偏高,误差不大于35%。 为了进一步验证在飞机机身结构常用的参数,即d/h= 3.5,Z≤20时曲板临界剪切应力系数曲线的适用性,增加了d/h= 3.5、Z= 5~20的11种构型的曲板,进行了屈曲计算和误差分析。 结果表明:对于2060-T8E30材料,在飞机机身结构常用的参数,即d/h= 3.5,Z≤20的情况下,当Z<10时,d/h= 3.5的曲板临界剪切应力系数曲线的适用性较好,误差不大于10%;当10 [1] 崔德刚. 结构稳定性设计手册[M]. 北京: 航空工业出版社,1996. [2] Batdorf S B, Stein M, Schildcrout M. Critical shear stress of curved rectangular panels[R]. NACA TN 1348, 1947. [3] Khun P, Peterson J P, Levin L R A. A summary of diagonal tension part I: methods of analysis[J]. NACA TN 2661, 1952. [4] 牛春匀,冯振宇,程小全,等. 实用飞机结构应力分析及尺寸设计[M]. 北京:航空工业出版社,2009. [5] 江丙云,孔祥宏,罗元元. ABAQUS 工程实例详解[M]. 北京:人民邮电出版社,2014. Research on Applicability of Critical Shear-stress Coefficients Curves curved panel; critical shear-stress coefficients curve; finite element; applicability 10.19416/j.cnki.1674-9804.2017.02.012 V215 A 孙 昊 男,硕士。主要研究方向:机体强度设计;E-mail: sunhao2@comac.cc 周良道 男,博士,研究员。主要研究方向:飞机设计;E-mail: zhouliangdao@comac.cc 郭伟毅 男,本科,高工。主要研究方向:机体强度设计;E-mail: guoweiyi@comac.cc 李三平 男,博士,研究员。主要研究方向:有限元技术;E-mail: lisanpingcomac.cc0 引言
1 曲板临界剪切应力的工程分析方法
2 曲板的结构尺寸
3 有限元分析
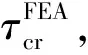
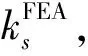
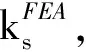

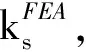
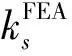

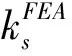
4 结论


