基于增益调度PID的四旋翼无人机主动容错控制

蒋银行，刘剑慰，杨 蒲，谢晓龙

(南京航空航天大学 自动化学院，江苏 南京 210016)

基于增益调度PID的四旋翼无人机主动容错控制

蒋银行，刘剑慰，杨 蒲，谢晓龙

(南京航空航天大学 自动化学院，江苏 南京 210016)

针对悬停状态下四旋翼无人机的执行机构故障，提出基于插值增益调度PID的主动容错控制方法，并在四旋翼无人工具实验平台上验证。首先根据不同故障率建立了故障模型集，并通过多模型故障诊断算法估计出故障的大小和时间。然后根据所估计出的故障大小，将控制律切换到相应故障情况下的控制律，实现对不同执行机构故障率的容错。最后在无人飞行工具实验平台上验证，飞行试验结果表明，与单纯的PID控制器相比，以插值增益调度PID为实现形式的主动容错控制方法可以使飞行器的容错性能有效提升。

四旋翼无人机；故障诊断；容错控制；插值增益调度PID

近几年，无人机(unmanned aerial vehicles，UAN)在民用和国防领域发挥着越来越重要的作用。在无人机中，四旋翼无人机因具有体积小、运动灵活、可定点悬停、可垂直起降、易于操控、生产简单等特点，在近地面侦察、救灾、航拍、农林植保等军事和民用领域得到了广泛的应用[1]。四旋翼无人机是一个典型的欠驱动不稳定对象，其动态特性具有强耦合、强非线性、多变量的特点，因此其飞行控制难度较大。不论是在正常状态下还是故障或者损伤状态下，安全性、可靠性、性能可接受性是衡量一个控制系统的重要指标[2-3]。

为了更广泛可靠的使用无人机，需要一些必要的措施，如容错性控制和故障检测、隔离、估计等方面提供安全保障，因此研究故障诊断和容错控制已成为无人机领域近几年的研究热点[4]。故障检测和诊断技术得到了深入、广泛的研究并取得了大量的应用成果，创造了巨大的经济效益[5-6]。容错控制可分为主动容错控制和被动容错控制。目前对被动容错控制研究较多，被动容错控制具有不需要获取故障信息的优点，但是也限制了容错控制的性能[7]；而主动容错控制则可以针对故障在线诊断，然后根据故障信息进行控制率的重构，最大程度发挥无人机的性能[8]。

目前四旋翼无人机的控制方法有：PID控制、反馈线性化、LQR控制[9]、滑模控制[10]、反步控制[11]、自适应控制[12]等。近几年，研究人员将研究的方向转移到无人机的故障诊断和容错控制。Zhang等[13-15]提出用预测控制、LQR控制、模型参考自适应控制对执行机构故障容错，并对滑模控制、反步控制、LQR控制等容错控制方法进行对比研究；文献[16]根据四旋翼无人机非线性数学模型，提出利用自适应滑模控制方法直接自修复无人机执行机构损伤，并在仿真环境下验证了方法的有效性；Cen等[4]提出基于非线性观测器的故障诊断方法，并应用到真实无人机物理平台，验证了方法在检测、隔离、估计故障方面具有一定的准确性；文献[17]提出了基于硬件冗余的无人机传感器故障诊断和容错控制，这种硬件冗余容错控制方法较为可靠；瑞士Meteomatics公司针对旋翼无人机空中突然失控的问题，提出用至少两个被动提升元件径向对称地安装于无人机偏航轴周围的方法，如出现失控坠落，这些扭转的提升元件能够围绕偏航启动旋转，旋转产生动态提升，从而降低了无人机的坠落和碰撞速度[18]。

但许多文献提出的故障诊断和容错控制方法仅在仿真环境下具有较好的诊断正确率和容错性能，在实际应用中会受到扰动、模型不确定性等因素影响，因此距离实际应用仍然有很多工作要做。由于PID控制器对模型的依赖小、相对可靠、简单、易于调节。在工业和航空应用领域使用较为广泛，由于四旋翼无人机的精确数学模型很难得到，所以目前对四旋翼无人机的控制以PID控制为主流。但是经典的PID控制不能满足飞行器在异常状态下的安全飞行。文献[19]中提出的增益调度PID主动容错控制，需要反复在线调节PID参数，增加了工作量，用Optitrack相机测高与高度指令产生残差来进行故障诊断的方法难以准确估计故障大小和发生时刻，容错控制效果有限。本文利用插值算法优化增益调度PID调参过程，减少了增益调度PID控制器调参的工作量，优化了容错控制性能；故障诊断方式也进行了改进，利用多模型故障诊断方法，能够较为准确、快速地估计出故障；最后在加拿大Quanser无人飞行器实验系统Qball-X4上进行了飞行实验验证。

图1 Qball-X4坐标系Fig.1 Qball-X4 axis

1 四旋翼无人机模型

通过运动学和动力学分析，建立四旋翼无人机的动态数学模型。对于四旋翼无人机的建模通常有两种方法：欧拉-牛顿法和欧拉-拉格朗日法。本文采用欧拉-牛顿法建立四旋翼无人机Qball-X4的数学模型。四旋翼Qball-X4的机体坐标系如图1所示，X、Y、Z轴分别代表滚转轴、俯仰轴、偏航轴。滚转角φ、俯仰角θ、偏航角ψ分别是围绕X，Y，Z轴旋转的角度。

1.1 执行机构动态模型

螺旋桨产生的推力使用一阶系统描述为

(1)

其中：K为电机推力系数，ω为电机带宽，ui为输入到电机的脉冲调宽度。这些变量的值见表1。执行机构的动态模型可用状态变量v表示为：

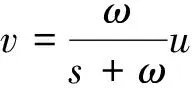
。 (2)表1 Qball-X4参数Tab. 1 Qball-X4 parameters

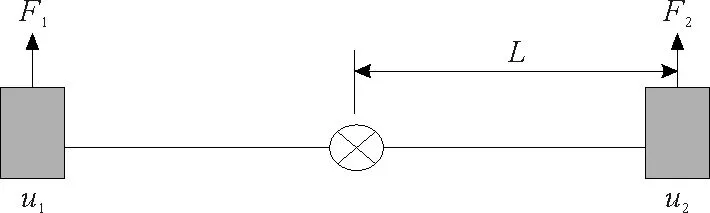
图2 滚转/俯仰运动模型Fig.2 Roll/pitch axis model

1.2 滚转/俯仰运动模型

假设关于X、Y轴的滚转运动和俯仰运动是解耦的，则滚转/俯仰运动可建模为如图2所示。每个电机产生的推力可以从式(1)计算出。滚转角/俯仰角可以用动态方程计算出：

(3)

其中：Jroll、Jpitch分别为滚转惯量、俯仰惯量，ΔF为对角线上两电机产生推力之差，L为螺旋桨中心到四旋翼飞行器重心的距离。

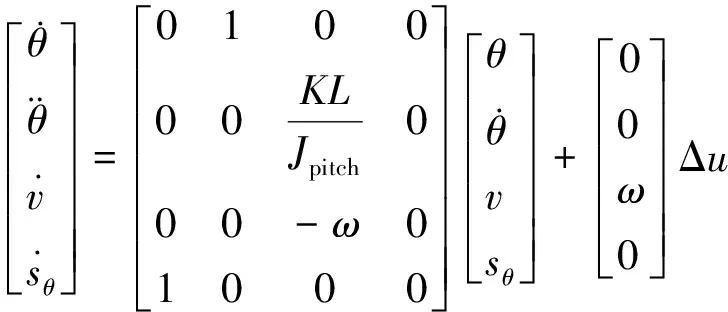
(4)

其中：Δu=u1-u2。类似可得滚转状态空间表达式。

1.3Z轴运动的动态模型

四旋翼飞行器沿Z轴方向运动的动态模型可描述为：

(5)

其中：M为四旋翼总质量，g为重力加速度。分析悬停状态下的容错控制，设滚转角φ和俯仰角θ均为0。基于小扰动原理，可将高度模型线性化为状态空间表达式：

(6)

1.4X/Y轴运动的动态模型

四旋翼飞行器沿X/Y轴运动的动态模型可描述为：

(7)

假设滚转角、俯仰角接近0，则X/Y轴运动的状态空间表达式为：

(8)

(9)

2 增益调度PID主动容错控制器

2.1 多模型故障诊断

多模型故障诊断采用分解合成的思路，适用于故障模式较多、模态切换频繁的系统。多模型故障诊断方法根据系统故障的不同，分别在相应故障模型的典型工作点上建立多个线性模型构成一个故障模型集，然后根据这些模型设计相应的滤波器。通过滤波，在线判断各模型的可能概率，最后通过概率合成，获得对系统故障模型的混合估计。多模型故障诊断算法结构如图3所示。

图3 多模型故障诊断算法结构图Fig.3 Structure of multiple model fault diagnosis algorithm

为估计执行器的故障状态，引入执行器的故障率模型。

γ=[γ1γ2γ3γ4]

0≤γn≤1,n=1,2,3,4

(11)

其中：γn用来描述第n个执行机构的故障程度。如果其值为1，则执行机构完全失效，其值为0，则执行机构正常。

考虑四个旋翼的失效情况，即[γ1γ2γ3γ4]，分别对应4个旋翼的故障率。鉴于实验安全，执行机构故障率γ取值为0～0.12。

图3中，ur为控制输入量，y为输出量，UAV为四旋翼无人机，ρ为故障模型估计值。根据文献[20]中经典交互多模型故障诊断算法估计出故障的大小、时间。故障模型估计值可与增益调度PID算法相匹配，即一个未知故障由多模型诊断出故障大小，再通过模态切换算法选择故障区域相对应的容错控制器。

2.2 增益调度PID控制器设计

所谓增益调度控制，就是利用辅助变量测出环境或者被控对象自身的变化，然后利用补偿控制器补偿变化量所引起的系统性能的降低。但是增益调度控制很难给出一个通用的控制率，对于每种情况必须单独处理，而且需要辅助变量测量出故障、扰动及被控对象的变化。为了克服增益调度的这些局限性，采用插值算法实现增益调度控制的优化。

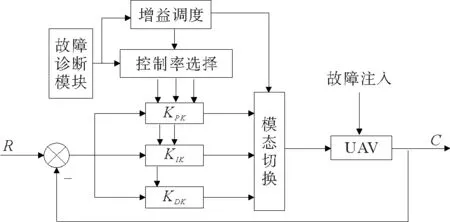
图4 插值增益调度PID实现框图Fig.4 Interpolated gain scheduled PID control表2 增益调度表Tab.2 Gain schedule table

段故障率/%KPKDKI120．3600．1600．310260．3760．1650．330390．3810．1680．3424110．4000．1700．350

增益调度的插值实现可预先选定系统的几个典型工作点，通过现场整定或在线优化确定好各工作点的控制器参数，构成一个调度表。系统实际运行时，根据故障率决策出补偿器的区域，而补偿器的参数在工作点之间通过内插来确定，从而生成全局的补偿器。

图4为增益调度控制器结构，由上、下两层构成，上层属于事件驱动层，完成增益调度，当系统注入不同的故障后，通过该层予以识别故障大小，进行PID参数切换，下层属于误差驱动层，由选定的模态直接实现控制。图中R、C分别表示设定值、输出值，KPk、KIk、KDk(k=1，2，…，N)为各模态的PID增益参数。为使控制律的设计简捷，各模态的控制律均采用了PID形式。

(12)

其中：KP、KI、KD分别为比例增益、积分增益、微分增益。

以多模型故障诊断模块输出的执行机构故障估计值ρ作为调度变量。考虑到实验安全的需要，现按执行机构故障率的百分数将系统的故障情况分割为4个区段：0～4%，4%～8%，8%～10%，10%～12%。各段中的2%、6%、9%、11%点是该系统的典型负荷点，作为各模态的中心点，在各区段分别设计好相应的控制律。这样，便可按下列步骤得到增益调度表，见表2。

有了增益调度表，就可根据不同故障率，使用插值方法重新设定PID参数。在插值计算中采用Lagrange插值公式：

(13)

其中：下标i和j代表执行机构故障率所在段号。例如，KPi和ρj分别代表所在第i段的比例增益和第j段的执行机构故障估计值，其余类推。

3 实验结果

3.1 经典PID控制

为实现无人机起飞、着陆的稳定性，实验起飞、着陆输入量均采用Sigmoid函数模块。当无人机悬停稳定后，注入6%执行器故障，高度变化如图5所示，下降高度为13.18 cm。经过4.28 s PID控制器调节后，无人机恢复到平衡位置。

当无人机悬停稳定后，注入12%执行器故障，高度变化如图6所示。可以看出，单纯的PID已经不能控制无人机恢复到平衡位置。因为在故障注入时，PID输出的控制量将变为原来的88%，四个电机带动螺旋桨产生的空气动力将小于无人机的重力，无人机下降速度较快。此时的PID输出控制量已不稳定，所以会出现飞行器震荡的现象。此外，PID恢复稳态能力和油门限幅值有一定关系。高度PID控制器输出值需先经过限幅处理，再输出给油门，防止某时刻输出油门值过大，造成过冲，使系统难以稳定，本文将限幅设为-0.143 1～0.300 0。值得注意的是，PID控制器输出量的限幅值过小和电池电压过低会减弱飞行器恢复稳态的能力。

图5 执行机构6%故障时经典PID控制效果Fig.5 PID controller effect in the presence of a 6% fault in all actuators

图6 执行机构12%故障时经典PID控制效果Fig.6 PID control effect in the presence of a 12% fault in all actuators

3.2 增益调度PID控制

使用增益调度PID控制算法，执行机构的故障率提升为12%时，无人机仍然能够恢复到稳态，实验结果如图7所示，飞行高度下降了11.26 cm。经过5.1 s增益调度PID调节后，虽然有小幅度超调，但是却使四旋翼飞行器降幅减少从而重新达到稳态，因此相对于经典PID，插值增益调度PID能够较好地处理故障状态，具有较好的容错控制性能。

为进一步验证提出的插值增益调度控制算法，设置一次飞行中存在不同故障率来验证无人机容错控制能力。实验结果如图8所示，当第一次注入6%执行器故障时，无人机高度下降3.13 cm，增益调度作用下，2.14 s后又恢复到稳态；当第二次注入12%故障时，无人机高度下降7.57 cm，增益调度作用下，4.8 s后又恢复到稳态。

从实验结果图5可知经典PID控制器在起飞、悬停阶段控制效果良好，能够达到较高的悬停精度，且能够处理较小的执行机构故障。从实验结果图6可知，在无人机悬停稳定后，注入12%执行机构损伤故障，四旋翼触到地面，系统已经不稳定。所以单纯的PID不能够调节更大的执行机构故障。对比图5、图6、图8可知，插值增益调度容错控制方法减小了无人机恢复稳态的时间和下降幅度，且能够处理较大的执行机构故障。

图7 执行机构12%故障时插值增益调度PID控制效果Fig.7 IGS-PID control effect in presence of a 12% fault in all actuators

图8 注入6%和12%故障时增益调度控制效果Fig.8 IGS-PID control effect in presence of a 6% and 12% fault in all actuators

以上分析可以看出，故障检测时间、大小对于无人机可接受的稳定性能是非常重要的。如果故障检测时间太长，即使故障诊断模块能够准确检测故障，但对容错控制提供的信息有效性较低。

4 小结与展望

本文将多模型故障诊断方法与插值增益调度控制方法相结合，并应用于真实四旋翼无人机飞行试验中。可以对一定的执行机构部分损伤起到主动容错控制功能，有一定的工程参考价值。并将插值增益调度PID与经典PID控制器进行对比，插值增益调度PID可以调节较大的执行机构故障，而且具有较快的调节能力。未来研究将考虑利用观测器进行故障估计，以便更为快速、准确的估计出故障发生的时间、大小，为容错控制提供更有效的信息，并进一步研究更有效的容错控制方法，应用于无人机俯仰、滚转、偏航通道。

[1]ZHAO B,XIAN B,ZHANG Y,et al.Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology[J].IEEE Transactions on Industrial Electronics,2015,62(5):2891-2902.

[2]LIU C L,PAN J,CHANG Y F.PID and LQR trajectory tracking control for an unmanned quadrotor helicopter:experimental studies[C] // Proceedings of the 35th Chinese Control Conference CCC 2016.Chengdu:IEEE Computer Society,2016:10845-10850.

[3]SADEGHZADEH I,ZHANG Y M.A review on fault-tolerant control for unmanned aerial vehicles(UAVs)[C]//AIAA Infotech at Aerospace Conference and Exhibit 2011.St.Louis:American Institute of Aeronautics and Astronautics Inc.,2011:1-12.

[4]CEN Z H,NOURA H,SUSILO T,et al.Engineering implementation on fault diagnosis for quadrotors based on nonlinear observer[C]//2013 25th Chinese Control and Decision Conference,CCDC 2013.Guiyang:IEEE Computer Society,2013:2971-2975.

[5]姜斌,冒泽慧,杨浩，等.控制系统的故障诊断与故障调节[M].北京:国防工业出版社,2009:2-3.

[6]周东华,叶银忠.现代故障诊断与容错控制[M].北京:清华大学出版社,2000:3-8.

[7]ZHANG Y M,JIANG J.Bibliographical review on reconfigurable fault-tolerant control systems[J].Annual Reviews in Control,2008,32(2):229-252.

[8]SADEGHZADEH I,MEHTA A,ZHANG Y M.Fault/Damage tolerant control of a quadrotor helicopter UAV using model reference adaptive control and gain-scheduled PID[C]//AIAA Guidance Navigation and Control Conference.American Institute of Aeronautics and Astronautics Inc.,2011:1-13.

[9]BIN F,JIA S,YAO Y.A LQR controller for quadrotor:Design and experiment[C]//2016 31st Youth Academic Annual Conference of Chinese Association of Automation.Wuhan:Institute of Electrical and Electronics Engineers Inc.,2016:81-86.

[10]BESNARD L,SHTESSEL Y B,LANDRUM B.Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer[J].Journal of the Franklin Institute,2012,349(2):658-684.

[11]DAS A,LEWIS F,SUBBARAO K.Backstepping approach for controlling a quadrotor using lagrange form dynamics[J].Journal of Intelligent and Robotic Systems:Theory and Applications,2009,56(1-2):127-151.

[12]WHITEHEAD B.T,BIENIAWSKI S.R.Model reference adaptive control of a quadrotor UAV[C]// AIAA Guidance Navigation and Control Conference.Toronto:American Institute of Aeronautics and Astronautics Inc.,2010:1-13.

[13]WANG H H,ZHANG Y M,YI Y M,et al.Nonlinear Tracking control methods applied to qball-X4 quadrotor UAV against actuator faults[C]// Proceedings of the 28th Chinese Control and Decision Conference.Yinchuan:Institute of Electrical and Electronics Engineers Inc.,2016:3478-3483.

[14]YU B,ZHANG Y M,MINCHALA I,et al.Fault-tolerant control with linear quadratic and model predictive control techniques against actuator faults in a quadrotor UAV [C]// 2nd International Conference on Control and Fault-Tolerant Systems,SysTol.Nice:IEEE Computer Society,2013:661-666.

[15]LIU Z X.,YUAN C.,ZHANG Y M,et al.A learning-based fault tolerant tracking control of an unmanned quadrotor helicopter[J].Journal of Intelligent and Robotic Systems:Theory and Applications,2016,84(1-4):145-162.

[16]YANG H L,JIANG B,ZHANG K.Direct self-repairing control of the quadrotor helicopter based on adaptive sliding mode control technique[C]// Proceedings of 2014 IEEE Chinese Guidance Navigation and Control Conference.Yantai:Institute of Electrical and Electronics Engineers Inc.,2014:1403-1408.

[17]DRAK A,NOURA H,HEJASE M.Sensor fault diagnostic and fault-tolerant control for the altitude control of a quadrotor UAV[C]//2015 IEEE 8th GCC Conference and Exhibition.Muscat:Institute of Electrical and Electronics Engineers Inc.,2015:1-5.

[18]王婷,张海.永不炸机！看看瑞士Meteomatics的最新专利[EB/OL].(2017-03-01)/[2017-04-03] http://www.81uav.cn/uav-news/201703/01/23200.html.

[19]SADEGHZADEH I,MEHTA A,CHAMSEDDINE A,et al.Active fault tolerant control of a quadrotor UAV based on gainscheduled PID control[C]//25th IEEE Canadian Conference on Electrical and Computer Engineering:Vision for a Greener Future.Montreal:IEEE Computer Society,2012:1-4.

[20]徐雪松.四旋翼无人机的多模型故障诊断[J].计算机工程与应用,2016,52(21):252-257. XU Xuesong.Multiple model fault diagnosis method for quadrotor UAV[J].Computer Engineering and Applications,2016,52(21):252-257.

(责任编辑：李 磊)

Active Fault Tolerant Control for Quadrotor UAV Based on Gain Scheduled PID

JIANG Yinhang, LIU Jianwei, YANG Pu, XIE Xiaolong

(College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, Jiangsu 210016, China)

In this paper, an active fault tolerant control method based on interpolated gain scheduled PID (IGS-PID) was proposed and tested on the experimental flatform to accommodate the failure of hovering UAV actuator’s fault. Firstly, a fault model set was established according to different failure rates and the multiple model fault diagnosis algorithm was used to estimate the size and time of the fault. Secondly, based on the estimated fault size, the control law was switched to the corresponding fault control law to realize different faults tolerant control. Finally, the proposed method was verified at the experimental platform. The flight test results show that compared with the simple PID controller, the active fault tolerant control method based on interpolated gain scheduled PID can effectively enhance the quadrotor’s fault tolerant performance.

quadrotor UVA; fault diagnosis; fault tolerant control; interpolated gain scheduled PID

2017-03-01

国家自然科学基金项目(61533008)；国家商用飞机制造工程技术研究中心创新基金项目(SAMC14-JS-15-053)；中央高校基本科研业务费专项资金(NJ20150011)

蒋银行(1991—)，男，江苏徐州人，硕士研究生，研究方向为故障诊断与容错控制. 刘剑慰(1977—)，男，江西南昌人，副教授，博士，研究领域为系统故障诊断与容错控制、先进飞行控制技术，本文通信作者.E-mail:ljw301@nuaa.edu.cn

TQ35

A

1672-3767(2017)04-0031-07

10.16452/j.cnki.sdkjzk.2017.04.005